2021-2022学年苏科版七年级数学下册7.4认识三角形 课件(共27张PPT)
文档属性
| 名称 | 2021-2022学年苏科版七年级数学下册7.4认识三角形 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 880.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览





文档简介
(共27张PPT)
7.4 认识三角形(1)
衣
食
住
行
活动1
认识三角形
从播放的图片中抽象出的三角形有什么共同的特点呢?你能发现你能概括出三角形的概念么?
新知(活动)
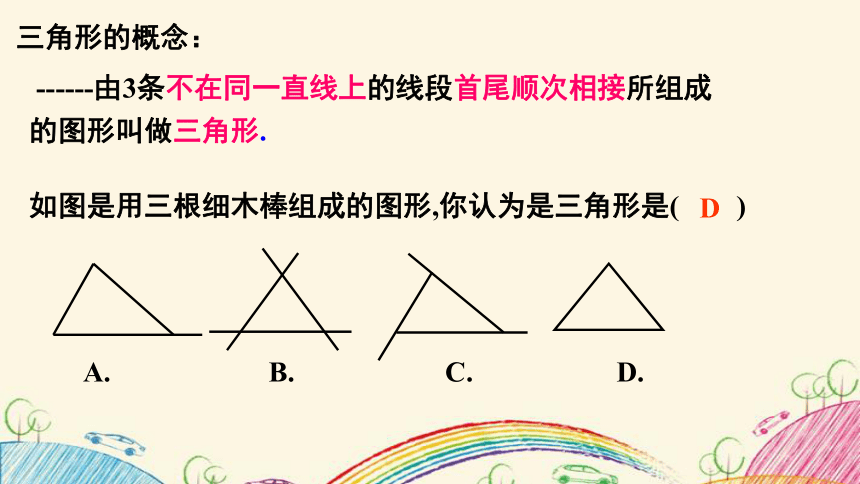
如图是用三根细木棒组成的图形,你认为是三角形是( )
A. B. C. D.
D
------由3条不在同一直线上的线段首尾顺次相接所组成的图形叫做三角形.
三角形的概念:
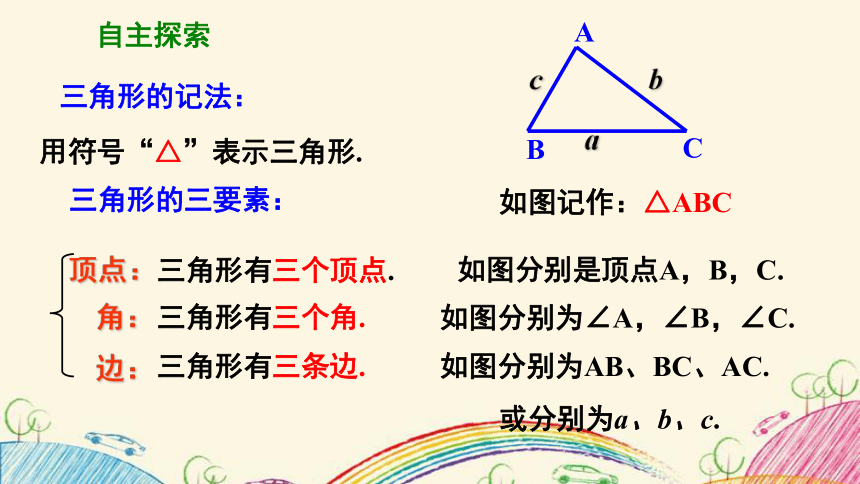
三角形的记法:
A
B
C
用符号“△”表示三角形.
三角形的三要素:
角:
顶点:
边:
三角形有三个角.
三角形有三个顶点.
如图分别为AB、BC、AC.
自主探索
如图记作:△ABC
如图分别为∠A,∠B,∠C.
如图分别是顶点A,B,C.
三角形有三条边.
a
b
c
或分别为a、b、c.
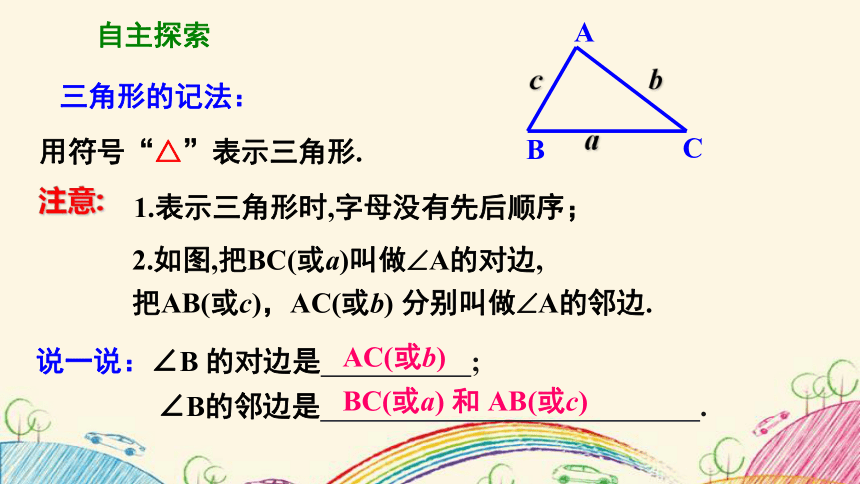
三角形的记法:
A
B
C
用符号“△”表示三角形.
自主探索
a
b
c
注意:
1.表示三角形时,字母没有先后顺序;
2.如图,把BC(或a)叫做 A的对边,
把AB(或c),AC(或b) 分别叫做 A的邻边.
说一说:∠B 的对边是 ;
∠B的邻边是 .
AC(或b)
BC(或a) 和 AB(或c)
3
△ABC,△ADC,△BDC
BC AC AB
∠A ∠B ∠ACB
CD AC ∠ADC
CD BC ∠BDC
ACD中,
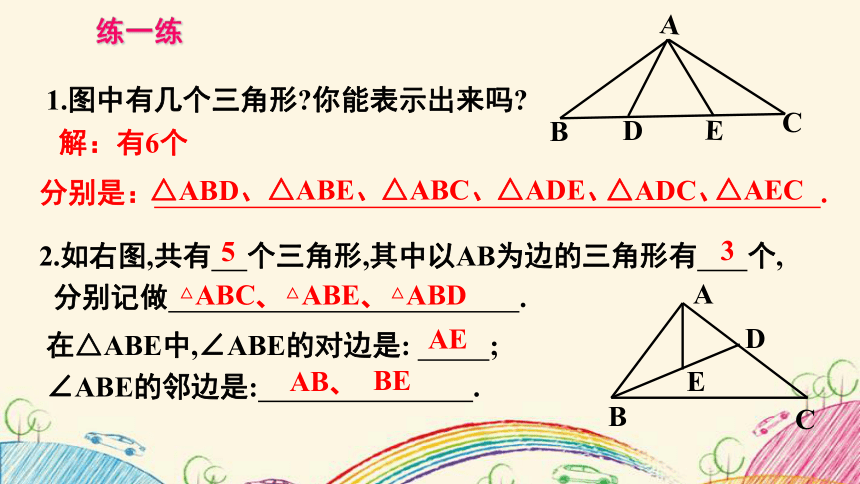
1.图中有几个三角形 你能表示出来吗
A
B
C
D
E
练一练
解:有6个
分别是: .
△ADC、
△ADE、
△ABC、
△ABE、
△AEC
△ABD、
2.如右图,共有 个三角形,其中以AB为边的三角形有 个,
分别记做 .
A
B
C
D
E
5
3
△ABC、△ABE、△ABD
在△ABE中,∠ABE的对边是: ;
∠ABE的邻边是: .
AE
AB、
BE
B
D
C
E
A
尝试写出图中的所有三角形.
7.4 认识三角形(1)
锐角三角形
直角三角形
钝角三角形
①
③
④
⑤
⑥
②
③
①
④
⑤
⑥
1.将三角形的序号填入相关的椭圆框内
②
C
(1) (2) (3)
所有内角都是锐角的三角形叫 ;
有一个内角是直角的三角形叫 ;
有一个内角是钝角的三角形叫 .
锐角三角形
直角三角形
钝角三角形
锐角三角形
直角三角形
钝角三角形
自主探索
发现:
一个三角形中最多有一个直角或一个钝角.
2.观察下面的三角形:
其中,是锐角三角形的是 ;
是直角三角形的是 ;
是钝角三角形的是 .(填标号)
(1)
(2)
(3)
(6)
(5)
(4)
(7)
练一练
(1)
(2)
(3)
(6)
(5)
(4)
(7)
3.在上面的三角形中, 有等腰三角形吗
等腰三角形:有两边相等的三角形是等腰三角形.
等腰三角形
等边三角形
不等边三角形
自主探索
按边分
按角分
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
三角形的分类:
自主探索
数学实验室
从长度分别为3cm、4cm、5cm、6cm和9cm的小木棒(如图)中任意取三根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
6cm
9cm
想一想
取3cm、5cm、9cm的能搭成吗 三边需要满足什么关系?
选择的长度 能否搭出三角形 三边的数量关系
能 不能
3cm,4cm,5cm √ 3+4 5
3cm,4cm,6cm √ 3+4 6
3cm,5cm,6cm √ 3+5 6
4cm,5cm,6cm √ 4+5 6
4cm,6cm,9cm √ 4+6 9
5cm,6cm,9cm √ 5+6 9
3cm,5cm,9cm √ 3+5<9
3cm,6cm,9cm √ 3+6=9
3cm,4cm,9cm √ 3+4<9
4cm,5cm,9cm √ 4+5=9
问题:
你发现三角形的三边之间有怎样的关系?
结论:
三角形的任意两边之和大于第三边。
1.任意画一个三角形,量出它的三边长度.
2.计算每个三角形的任意两边之和,
并与第三边比较,你能得到什么结论?
议一议
C
A
B
b
c
a
三角形任意两边之和大于第三边.
你知道为什么吗
根据是:两点之间, 线段最短.
a+b>c; b+c>a; c+a>b.
1.任意画一个三角形,量出它的三边长度.
2.计算每个三角形的任意两边之和,
并与第三边比较,你能得到什么结论?
议一议
C
A
B
b
c
a
三角形任意两边之和大于第三边.
3.计算每个三角形的任意两边之差,再与第三边比较,你又能得到什么结论?
三角形任意两边之差小于第三边.
两边之差
第三边
两边之和
<
<
(1) 5cm, 8cm, 2cm (2) 3cm, 3cm, 4cm
解:
(1)因为5 + 2 = 7< 8, 不满足两边之和大于第三边,
所以不能摆成三角形.
友情提醒:
只需比较两条较短线段之和与最长线段的大小.
(3) 5cm,8cm,13cm (4) 3.5cm,7.5cm,4.5cm
例1:下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题讲解
(1) 5cm, 8cm, 2cm (2) 3cm, 3cm, 4cm
解:
(3) 5cm,8cm,13cm (4) 3.5cm,7.5cm,4.5cm
例1:下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题讲解
(2) 因为3+3 = 6 > 4,满足两边之和大于第三边,
所以能摆成三角形.
(3)因为5+8=13, 不满足两边之和大于第三边,
所以不能摆成三角形.
(4)因为3.5 + 4.5 =8>7.5,满足两边之和大于第三边,
所以能摆成三角形.
反馈练习:
2.以下列长度的三条线段为边,能构成三角形的是( )
A.6 cm,8 cm,10 cm;
B.3 cm,8 cm,11 cm;
C.3 cm,4 cm,10 cm;
D.三条线段的长度之比为5∶6∶13.
A
解析:在判断时一般检查较短的两边之和是否大于最长边.
(1)等腰三角形的一边长为4cm,另一边长为5cm,
则周长为_____________;
(2)等腰三角形的一边长为4cm,另一边长为9cm,
则周长为____________.
4,4,5
5,5,4
13cm或14cm
9,9,4
22cm
4,4,9
有两根长度分别为4cm和7cm的木棒,
(1)再取一根长度为2cm的木棒,它们能摆成三角形 为什么
(2)如果取一根长度为11cm的木棒呢
(3)第三边在什么范围内?
(4)如果第三边是正整数,那么第三边可能是哪几个数
思考题
解:(1)不能,因为2+4<7,所以不能摆成.
(2)能,因为4+7>11,所以能摆成.
(3)第三条边范围大于3cm,小于11cm
(1)3cm, 4cm, 5cm ; ( ) (2)8cm, 7cm, 15cm;( )
(3) 13cm, 12cm, 20cm; ( ) (4)5cm, 5cm, 11cm. ( )
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗
能
练一练
不能
能
不能
若第三边为偶数,那么三角形的周长是 .
2.如果三角形的两边长分别是2和4,且第三边是正整数,那么第三边长为 .
3、4、5
10
若第三边为奇数,那么第三边长为 .
3或5
所作出的三角形的周长最长是
11
若a,b,c是△ABC的三边,化简:
因为a+b>c,a+c>b,b+c>a
所以上式=a+b-c+c+a-b+b+c-a
=a+b+c
所以a+b-c>0,b-(c+a)<0,a-(b+c)<0
小结:
通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢,说出来告诉大家.
7.4 认识三角形(1)
衣
食
住
行
活动1
认识三角形
从播放的图片中抽象出的三角形有什么共同的特点呢?你能发现你能概括出三角形的概念么?
新知(活动)
如图是用三根细木棒组成的图形,你认为是三角形是( )
A. B. C. D.
D
------由3条不在同一直线上的线段首尾顺次相接所组成的图形叫做三角形.
三角形的概念:
三角形的记法:
A
B
C
用符号“△”表示三角形.
三角形的三要素:
角:
顶点:
边:
三角形有三个角.
三角形有三个顶点.
如图分别为AB、BC、AC.
自主探索
如图记作:△ABC
如图分别为∠A,∠B,∠C.
如图分别是顶点A,B,C.
三角形有三条边.
a
b
c
或分别为a、b、c.
三角形的记法:
A
B
C
用符号“△”表示三角形.
自主探索
a
b
c
注意:
1.表示三角形时,字母没有先后顺序;
2.如图,把BC(或a)叫做 A的对边,
把AB(或c),AC(或b) 分别叫做 A的邻边.
说一说:∠B 的对边是 ;
∠B的邻边是 .
AC(或b)
BC(或a) 和 AB(或c)
3
△ABC,△ADC,△BDC
BC AC AB
∠A ∠B ∠ACB
CD AC ∠ADC
CD BC ∠BDC
ACD中,
1.图中有几个三角形 你能表示出来吗
A
B
C
D
E
练一练
解:有6个
分别是: .
△ADC、
△ADE、
△ABC、
△ABE、
△AEC
△ABD、
2.如右图,共有 个三角形,其中以AB为边的三角形有 个,
分别记做 .
A
B
C
D
E
5
3
△ABC、△ABE、△ABD
在△ABE中,∠ABE的对边是: ;
∠ABE的邻边是: .
AE
AB、
BE
B
D
C
E
A
尝试写出图中的所有三角形.
7.4 认识三角形(1)
锐角三角形
直角三角形
钝角三角形
①
③
④
⑤
⑥
②
③
①
④
⑤
⑥
1.将三角形的序号填入相关的椭圆框内
②
C
(1) (2) (3)
所有内角都是锐角的三角形叫 ;
有一个内角是直角的三角形叫 ;
有一个内角是钝角的三角形叫 .
锐角三角形
直角三角形
钝角三角形
锐角三角形
直角三角形
钝角三角形
自主探索
发现:
一个三角形中最多有一个直角或一个钝角.
2.观察下面的三角形:
其中,是锐角三角形的是 ;
是直角三角形的是 ;
是钝角三角形的是 .(填标号)
(1)
(2)
(3)
(6)
(5)
(4)
(7)
练一练
(1)
(2)
(3)
(6)
(5)
(4)
(7)
3.在上面的三角形中, 有等腰三角形吗
等腰三角形:有两边相等的三角形是等腰三角形.
等腰三角形
等边三角形
不等边三角形
自主探索
按边分
按角分
锐角三角形
直角三角形
钝角三角形
不等边三角形
等腰三角形
等边三角形
三角形的分类:
自主探索
数学实验室
从长度分别为3cm、4cm、5cm、6cm和9cm的小木棒(如图)中任意取三根,能否搭成一个三角形?请试一试.
3cm
4cm
5cm
6cm
9cm
想一想
取3cm、5cm、9cm的能搭成吗 三边需要满足什么关系?
选择的长度 能否搭出三角形 三边的数量关系
能 不能
3cm,4cm,5cm √ 3+4 5
3cm,4cm,6cm √ 3+4 6
3cm,5cm,6cm √ 3+5 6
4cm,5cm,6cm √ 4+5 6
4cm,6cm,9cm √ 4+6 9
5cm,6cm,9cm √ 5+6 9
3cm,5cm,9cm √ 3+5<9
3cm,6cm,9cm √ 3+6=9
3cm,4cm,9cm √ 3+4<9
4cm,5cm,9cm √ 4+5=9
问题:
你发现三角形的三边之间有怎样的关系?
结论:
三角形的任意两边之和大于第三边。
1.任意画一个三角形,量出它的三边长度.
2.计算每个三角形的任意两边之和,
并与第三边比较,你能得到什么结论?
议一议
C
A
B
b
c
a
三角形任意两边之和大于第三边.
你知道为什么吗
根据是:两点之间, 线段最短.
a+b>c; b+c>a; c+a>b.
1.任意画一个三角形,量出它的三边长度.
2.计算每个三角形的任意两边之和,
并与第三边比较,你能得到什么结论?
议一议
C
A
B
b
c
a
三角形任意两边之和大于第三边.
3.计算每个三角形的任意两边之差,再与第三边比较,你又能得到什么结论?
三角形任意两边之差小于第三边.
两边之差
第三边
两边之和
<
<
(1) 5cm, 8cm, 2cm (2) 3cm, 3cm, 4cm
解:
(1)因为5 + 2 = 7< 8, 不满足两边之和大于第三边,
所以不能摆成三角形.
友情提醒:
只需比较两条较短线段之和与最长线段的大小.
(3) 5cm,8cm,13cm (4) 3.5cm,7.5cm,4.5cm
例1:下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题讲解
(1) 5cm, 8cm, 2cm (2) 3cm, 3cm, 4cm
解:
(3) 5cm,8cm,13cm (4) 3.5cm,7.5cm,4.5cm
例1:下面分别是三根小木棒的长度,用它们能摆成三角形吗
例题讲解
(2) 因为3+3 = 6 > 4,满足两边之和大于第三边,
所以能摆成三角形.
(3)因为5+8=13, 不满足两边之和大于第三边,
所以不能摆成三角形.
(4)因为3.5 + 4.5 =8>7.5,满足两边之和大于第三边,
所以能摆成三角形.
反馈练习:
2.以下列长度的三条线段为边,能构成三角形的是( )
A.6 cm,8 cm,10 cm;
B.3 cm,8 cm,11 cm;
C.3 cm,4 cm,10 cm;
D.三条线段的长度之比为5∶6∶13.
A
解析:在判断时一般检查较短的两边之和是否大于最长边.
(1)等腰三角形的一边长为4cm,另一边长为5cm,
则周长为_____________;
(2)等腰三角形的一边长为4cm,另一边长为9cm,
则周长为____________.
4,4,5
5,5,4
13cm或14cm
9,9,4
22cm
4,4,9
有两根长度分别为4cm和7cm的木棒,
(1)再取一根长度为2cm的木棒,它们能摆成三角形 为什么
(2)如果取一根长度为11cm的木棒呢
(3)第三边在什么范围内?
(4)如果第三边是正整数,那么第三边可能是哪几个数
思考题
解:(1)不能,因为2+4<7,所以不能摆成.
(2)能,因为4+7>11,所以能摆成.
(3)第三条边范围大于3cm,小于11cm
(1)3cm, 4cm, 5cm ; ( ) (2)8cm, 7cm, 15cm;( )
(3) 13cm, 12cm, 20cm; ( ) (4)5cm, 5cm, 11cm. ( )
1.下列每组数分别是三根小木棒的长度,用它们能摆成三角形吗
能
练一练
不能
能
不能
若第三边为偶数,那么三角形的周长是 .
2.如果三角形的两边长分别是2和4,且第三边是正整数,那么第三边长为 .
3、4、5
10
若第三边为奇数,那么第三边长为 .
3或5
所作出的三角形的周长最长是
11
若a,b,c是△ABC的三边,化简:
因为a+b>c,a+c>b,b+c>a
所以上式=a+b-c+c+a-b+b+c-a
=a+b+c
所以a+b-c>0,b-(c+a)<0,a-(b+c)<0
小结:
通过今天的学习,你学会了什么?你会正确运用吗?通过这节课的学习,你有什么感受呢,说出来告诉大家.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
