2021-2022学年北师大版九年级数学下册3.3垂径定理 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理 解答题专题提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 548.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 19:13:36 | ||
图片预览



文档简介
2021-2022学年北师大版九年级数学下册《3-3垂径定理》解答题专题提升训练(附答案)
1.如图,CD为⊙O的直径,弦AB⊥CD于E,如果CE=1,AB=10,求半径OC的长.
2.好山好水好绍兴,石拱桥在绍兴处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面AB宽度16m时,拱顶高出水平面4m,货船宽12m,船舱顶部为矩形并高出水面3m.
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
3.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
4.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
5.如图,锐角△ABC内接于 O,BE⊥AC于点D,交O于点E,DF⊥BC于点F,DE=DF,连接AE.
(1)求证:AE=BD.
(2)若CD=1,AE=2,求⊙O的半径及AB的长.
6.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,BC=3.
(1)求AB的长;
(2)求⊙O的半径.
7.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
8.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
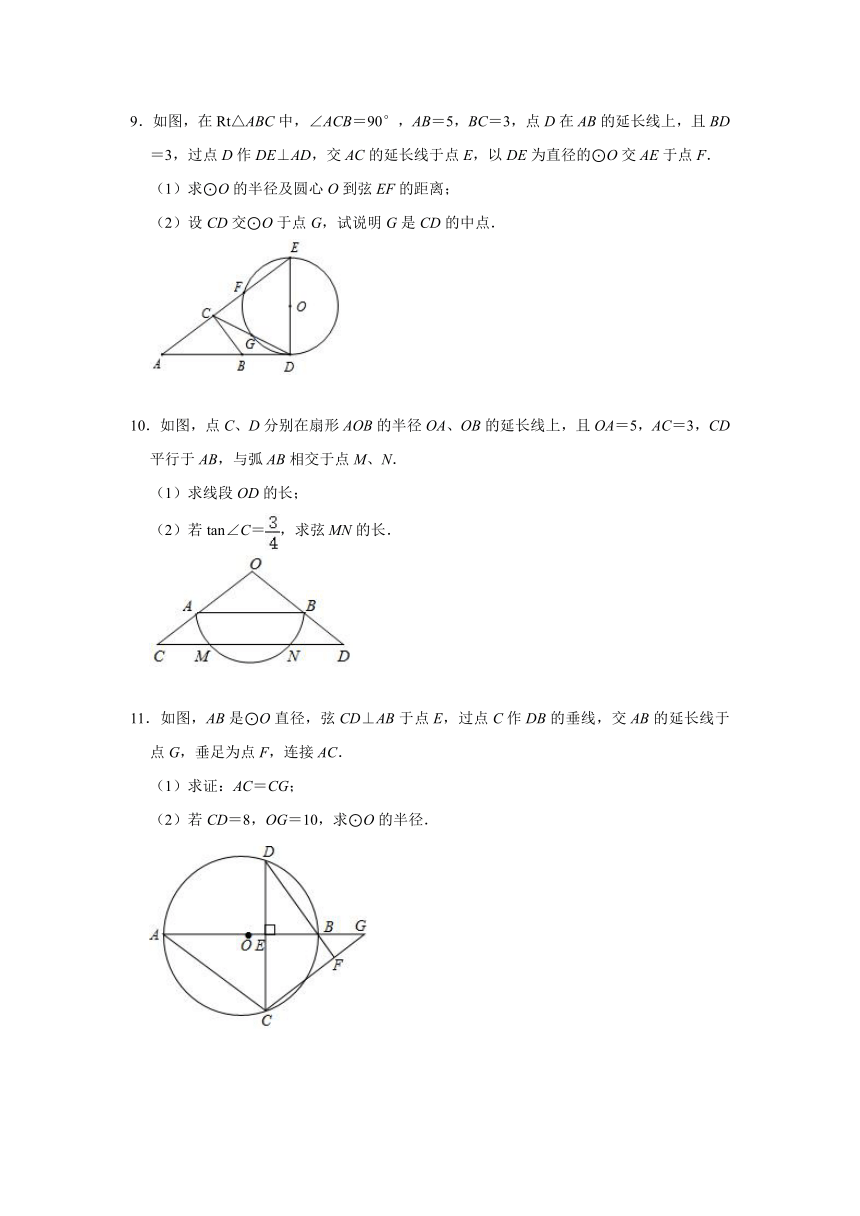
9.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D在AB的延长线上,且BD=3,过点D作DE⊥AD,交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径及圆心O到弦EF的距离;
(2)设CD交⊙O于点G,试说明G是CD的中点.
10.如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=5,AC=3,CD平行于AB,与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若tan∠C=,求弦MN的长.
11.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=8,OG=10,求⊙O的半径.
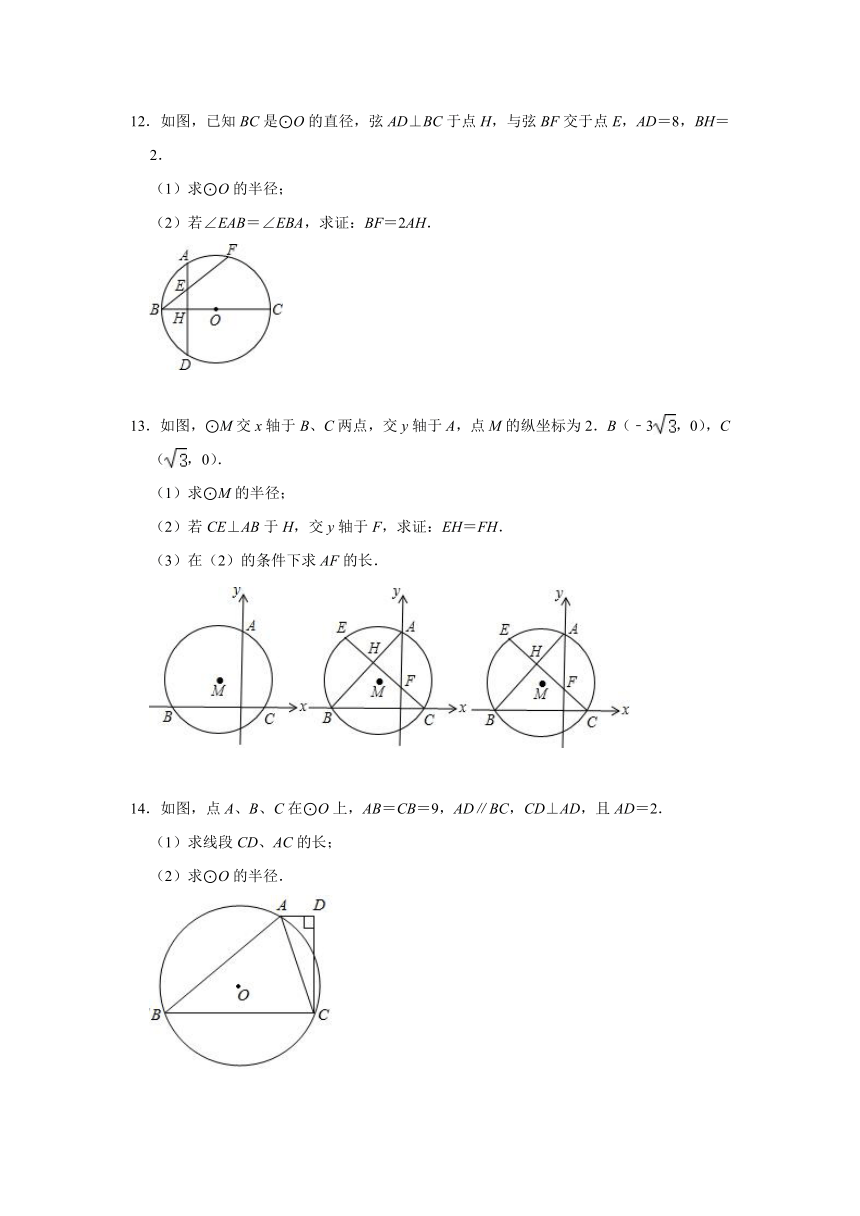
12.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)若∠EAB=∠EBA,求证:BF=2AH.
13.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
14.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
15.如图,四边形ABCD内接于⊙O,CD∥AB,且AB是⊙O的直径,AE⊥CD交CD的延长线于点E,若AE=2,CD=3.
(1)求⊙O的直径;
(2)若翻折使点B与E重合的直线l(折痕)交⊙O于P,Q两点,求△BPQ的面积.
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,A,B,C,D在⊙O上,AB∥CD,经过圆心O的线段EF⊥AB于点F,与CD交于点E.
(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;
(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.
18.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
19.已知:点A(﹣1﹣,0),B(0,1+),过A、B两点作直线l,以点C(0,)为圆心,为半径作圆C,直线l与圆C相交于M、N两点.
(1)求线段MN的长度.
(2)求∠MON的大小(O为坐标原点).
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径.
参考答案
1.解:连接OA,
∵CD是⊙O的直径,AB⊥CD,
∴AE=BE
∵AB=10
∴AE=5
设OA=R
∴OE=R﹣1
根据勾股定理:R2=52+(R﹣1)2
解得R=13,
∴半径OC的长为13.
2.解:(1)如图,连接OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=16m,
∴BD=AB=8m.
又∵CD=4m,
设OB=OC=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+82,
解得r=10.
答:此圆弧形拱桥的半径为10米.
(2)连接ON
∵CD=4m,船舱顶部为长方形并高出水面3m,
∴CE=4﹣3=1(m),
∴OE=r﹣CE=10﹣1=9(m),
在Rt△OEN中,EN2=ON2﹣OE2=102﹣92=19,
∴EN=(m).
∴MN=2EN=2m<12m.
∴此货船B不能顺利通过这座拱桥.
3.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
4.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
5.(1)证明:∵BE⊥AC,DF⊥BC,
∴∠ADE=∠BFD=90°,
由圆周角定理得:∠EAD=∠CBD,
在△EAD和△DBF中,
,
∴△EAD≌△DBF(AAS),
∴AE=BD;
(2)解:过O作OH⊥AB于H,连接OA、OB,
∵AE=2,AE=BD,
∴BD=2,
∵CD=1,
∴由勾股定理得:BC==3,
∵OH⊥AB,OA=OB,
∴AH=BH,∠BOH=AOB,
∵∠ACB=∠AOB,
∴∠ACB=∠HOB,
即cos∠HOB=cos∠ACB,
∴==,
设OH=x,则OB=3x,
∵△EAD≌△DBF,
∴DE=DF,
∵S△CDB==,
∴1×=3×DF,
解得:DF=,
即DE=DF=,
由勾股定理得:AD===,
∴AB===,
∴AH=BH=,
在Rt△BHO中,由勾股定理得:OH2+BH2=OB2,
x2+()2=(3x)2,
解得:x=,
∴半径OB的长度是3×=.
6.解:(1)连接AC,如图,
∵CD⊥AB,
∴AF=BF,即CD垂直平分AB,
∴CA=CB=3,
∵AO⊥BC,
∴CE=BE,即AE垂直平分BC,
∴AB=AC=3;
(2)∵AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴AE⊥BC,
∴AE平分∠BAC,即∠OAF=30°,
在Rt△OAF中,∵OF=AF=×=,
∴OA=2OF=,
即⊙O的半径为.
7.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
8.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
9.解:(1)过点O作OH⊥EF于H,
由勾股定理得,AC==4,
∵DE⊥AD,∠ACB=90°,
∴∠ACB=∠ADE,
∵∠C=∠C,
∴△ACB∽△ADE,
∴=,即=,
解得,DE=6,
∴⊙O的半径为3,
AE==10,
∵∠EHO=∠EDA,∠OEH=∠AED,
∴△EHO∽△EDA,
∴=,即=,
解得,OH=,
∴点O到EF距离为;
(2)连接EG,
∵AE=10,AC=4,
∴EC=6,
∴EC=ED,
∵DE是⊙O的直径,
∴EG⊥CD,
∴G是CD的中点.
10.解:(1)∵OA=OB,
∴∠OAB=∠OBA,
∵AB∥CD,
∴∠C=∠OAB,∠D=∠OBA,
∴∠C=∠D,
∴OD=OC=OA+AC=5+3=8;
(2)过O点作OE⊥MN于E,连接OM,如图,则ME=NE,
在Rt△OCE中,tanC==,
设OE=3x,则CE=4x,
∴OC=5x,
即5x=8,解得x=,
∴OE=,
在Rt△OME中,ME===,
∴MN=2ME=.
11.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG.
(2)解:设⊙O的半径为r.则AG=OA+OG=r+10,
∵CA=CG,CD⊥AB,
∴AE=EG=,EC=ED=4,
∴OE=AE﹣OA=,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=()2+42,
解得r=或(舍弃),
∴⊙O的半径为.
12.(1)解:连接OA交BF于G,如图,⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r﹣2,OA=r,
∴r2=42+(r﹣2)2
,解得r=5,
即⊙O的半径为5;
(2)方法一
证明:连接CF,如图,
∵AD⊥OB,
∴弧AB=弧DB,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴OA⊥BG,
∴BG=FG,
∴∠OAH=∠OBG,
在△OAH和△OBG中,
,
∴△OAH≌△OBG(AAS),
∴AH=BG,
∴BF=2AH.
方法二:∵AD⊥OB,
∴弧AB=弧DB,AH=DH,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴弧AD=弧BF,
∴BF=AD=2AH.
13.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
14.解:(1)作AE⊥BC于E,如图1所示:
则AE=DC,EC=AD=2,
∴BE=BC﹣EC=9﹣2=7,
∴CD=AE===4,
∴AC===6;
(2)作BF⊥AC于F,连接OA,如图2所示:
则AF=CF=AC=3,
∴BF垂直平分AC,
∴BF一定过圆心O,BF===6,
设⊙O的半径为r,则OF=6﹣r,
在Rt△OAF中,由勾股定理得:(6﹣r)2+32=r2,
解得:r=,
即⊙O的半径为.
15.解:(1)连接AC,∵AB∥CD且AE⊥CD,
∴AB⊥AE,∠ECA=∠BAC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=∠BAC+∠EAC=90°,
∴∠B=∠EAC,
∵∠ADE=∠B,
∴∠EAC=∠ADE,
∵∠E=∠AEC,
∴△ACE∽△DAE,
∴=,
∴AE2=ED EC,
设DE=x,则22=x(x+3),
解得:x1=1,x2=﹣4(舍去),
即:DE=1,
在Rt△ACE中,AC2=AE2+CE2,
∴AC2=20,
∵∠ACB=∠E,∠CAE=∠B,
∴△ACE∽△BAC,
∴=
∴AB=5;
(2)设BE与PQ交于G,AB与PQ交于F,
∵AE=2,AB=5,
∴BE==,
∵翻折使点B与E重合,
∴BG⊥PQ,BG=BE=,
∵∠BGF=∠EAB=90°,∠GBF=∠ABE,
∴△BGF∽△BAE,
∴=,
∴=,
∴BF=,
∴OF=﹣=,
过O作OH⊥于H,
∴OH∥BG,PQ=2HQ,
∴△OFH∽△BFG,
∴=,
∴=,
∴OH=,
连接OQ,
∴HQ==,
∴PQ=2HQ=,
∴△BPQ的面积=×=.
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.解:(1)如图1中,连接OB,OC.设BF=EF=x,OF=y.
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴∠CEF=∠BFO=90°
∴AF=BF=x,DE=EC=2,
根据勾股定理可得:,
解得(舍弃)或,
∴BF=4,AB=2BF=8.
(2)如图2中,作CH⊥AB于H.
∵OB⊥OC,
∴∠A=∠BOC=45°,
∵AH⊥CH,
∴△ACH是等腰直角三角形,
∵AC=CH,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∠CEF=∠EFH=∠CHF=90°,
∴四边形EFHC是矩形,
∴CH=EF,
在Rt△OEC中,∵EC=,OC=,
OE===2,
∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,
∴∠FOB=∠ECO,
∵OB=OC,
∴△OFB≌△CEO(AAS),
∴OF=EC=,
∴CH=EF=3,
∴AC=EF=6.
18.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
19.解:(1)作CH⊥MN于H,则H为MN的中点,
∵OB=1+,OC=
∴CB=1
又∵∠ABC=45°
∴CH=
连接CM、CN,在Rt△HCM中,
∵CH=,
又∵MC=
∴MH=,
∴MN=
(2)在Rt△MCH中,
∵CH=,
又∵MC=
∴∠MCH=60°
∴∠MCN=120°
∴∠MON=60°.
20.(1)证明:∵PD∥CB,∴=,∴∠FBC=∠FCB,∴FC=FB.
(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.
1.如图,CD为⊙O的直径,弦AB⊥CD于E,如果CE=1,AB=10,求半径OC的长.
2.好山好水好绍兴,石拱桥在绍兴处处可见,小明要帮忙船夫计算一艘货船是否能够安全通过一座圆弧形的拱桥,现测得桥下水面AB宽度16m时,拱顶高出水平面4m,货船宽12m,船舱顶部为矩形并高出水面3m.
(1)请你帮助小明求此圆弧形拱桥的半径;
(2)小明在解决这个问题时遇到困难,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
3.如图,AB为圆O直径,F点在圆上,E点为AF中点,连接EO,作CO⊥EO交圆O于点C,作CD⊥AB于点D,已知直径为10,OE=4,求OD的长度.
4.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=EG=8,求⊙O的半径.
5.如图,锐角△ABC内接于 O,BE⊥AC于点D,交O于点E,DF⊥BC于点F,DE=DF,连接AE.
(1)求证:AE=BD.
(2)若CD=1,AE=2,求⊙O的半径及AB的长.
6.如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,BC=3.
(1)求AB的长;
(2)求⊙O的半径.
7.如图,在平行四边形ABCD中,AB=5,BC=8,BC边上的高AH=3,点P是边BC上的动点,以CP为半径的⊙C与边AD交于点E,F(点E在点F的左侧).
(1)当⊙C经过点A时,求CP的长;
(2)连接AP,当AP∥CE时,求⊙C的半径及弦EF的长.
8.如图,AB是⊙O的直径,四边形ABCD内接于⊙O,OD交AC于点E,AD=CD.
(1)求证:OD∥BC;
(2)若AC=10,DE=4,求BC的长.
9.如图,在Rt△ABC中,∠ACB=90°,AB=5,BC=3,点D在AB的延长线上,且BD=3,过点D作DE⊥AD,交AC的延长线于点E,以DE为直径的⊙O交AE于点F.
(1)求⊙O的半径及圆心O到弦EF的距离;
(2)设CD交⊙O于点G,试说明G是CD的中点.
10.如图,点C、D分别在扇形AOB的半径OA、OB的延长线上,且OA=5,AC=3,CD平行于AB,与弧AB相交于点M、N.
(1)求线段OD的长;
(2)若tan∠C=,求弦MN的长.
11.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连接AC.
(1)求证:AC=CG;
(2)若CD=8,OG=10,求⊙O的半径.
12.如图,已知BC是⊙O的直径,弦AD⊥BC于点H,与弦BF交于点E,AD=8,BH=2.
(1)求⊙O的半径;
(2)若∠EAB=∠EBA,求证:BF=2AH.
13.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(﹣3,0),C(,0).
(1)求⊙M的半径;
(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.
(3)在(2)的条件下求AF的长.
14.如图,点A、B、C在⊙O上,AB=CB=9,AD∥BC,CD⊥AD,且AD=2.
(1)求线段CD、AC的长;
(2)求⊙O的半径.
15.如图,四边形ABCD内接于⊙O,CD∥AB,且AB是⊙O的直径,AE⊥CD交CD的延长线于点E,若AE=2,CD=3.
(1)求⊙O的直径;
(2)若翻折使点B与E重合的直线l(折痕)交⊙O于P,Q两点,求△BPQ的面积.
16.如图,点A,D,B,C在⊙O上,AB⊥BC,DE⊥AB于点E.若BC=3,AE=DE=1,求⊙O半径的长.
17.如图,A,B,C,D在⊙O上,AB∥CD,经过圆心O的线段EF⊥AB于点F,与CD交于点E.
(1)如图1,当⊙O半径为5,CD=4,若EF=BF,求弦AB的长;
(2)如图2,当⊙O半径为,CD=2,若OB⊥OC,求弦AC的长.
18.如图,AB为⊙O直径,点D为AB下方⊙O上一点,点C为弧ABD中点,连接CD,CA.
(1)求证:∠ABD=2∠BDC;
(2)过点C作CE⊥AB于H,交AD于E,求证:EA=EC;
(3)在(2)的条件下,若OH=5,AD=24,求线段DE的长
19.已知:点A(﹣1﹣,0),B(0,1+),过A、B两点作直线l,以点C(0,)为圆心,为半径作圆C,直线l与圆C相交于M、N两点.
(1)求线段MN的长度.
(2)求∠MON的大小(O为坐标原点).
20.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,且PD∥CB,弦PB与CD交于点F
(1)求证:FC=FB;
(2)若CD=24,BE=8,求⊙O的直径.
参考答案
1.解:连接OA,
∵CD是⊙O的直径,AB⊥CD,
∴AE=BE
∵AB=10
∴AE=5
设OA=R
∴OE=R﹣1
根据勾股定理:R2=52+(R﹣1)2
解得R=13,
∴半径OC的长为13.
2.解:(1)如图,连接OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=16m,
∴BD=AB=8m.
又∵CD=4m,
设OB=OC=r,则OD=(r﹣4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣4)2+82,
解得r=10.
答:此圆弧形拱桥的半径为10米.
(2)连接ON
∵CD=4m,船舱顶部为长方形并高出水面3m,
∴CE=4﹣3=1(m),
∴OE=r﹣CE=10﹣1=9(m),
在Rt△OEN中,EN2=ON2﹣OE2=102﹣92=19,
∴EN=(m).
∴MN=2EN=2m<12m.
∴此货船B不能顺利通过这座拱桥.
3.解:∵E点为AF中点,
∴OE⊥AF,
∵CO⊥EO,
∴OC∥AF,
∴∠OAE=∠COD,
∵CD⊥AB,
∴∠AEO=∠ODC,
在△AEO和△ODC中,
,
∴△AEO≌△ODC(AAS),
∴CD=OE=4,
∵OC=5,
∴OD===3.
4.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG;
(2)解:连接OC,如图,
设⊙O的半径为r.
∵CA=CG,CD⊥AB,
∴AE=EG=8,EC=ED=4,
∴OE=AE﹣OA=8﹣r,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=(8﹣r)2+42,
解得r=5,
∴⊙O的半径为5.
5.(1)证明:∵BE⊥AC,DF⊥BC,
∴∠ADE=∠BFD=90°,
由圆周角定理得:∠EAD=∠CBD,
在△EAD和△DBF中,
,
∴△EAD≌△DBF(AAS),
∴AE=BD;
(2)解:过O作OH⊥AB于H,连接OA、OB,
∵AE=2,AE=BD,
∴BD=2,
∵CD=1,
∴由勾股定理得:BC==3,
∵OH⊥AB,OA=OB,
∴AH=BH,∠BOH=AOB,
∵∠ACB=∠AOB,
∴∠ACB=∠HOB,
即cos∠HOB=cos∠ACB,
∴==,
设OH=x,则OB=3x,
∵△EAD≌△DBF,
∴DE=DF,
∵S△CDB==,
∴1×=3×DF,
解得:DF=,
即DE=DF=,
由勾股定理得:AD===,
∴AB===,
∴AH=BH=,
在Rt△BHO中,由勾股定理得:OH2+BH2=OB2,
x2+()2=(3x)2,
解得:x=,
∴半径OB的长度是3×=.
6.解:(1)连接AC,如图,
∵CD⊥AB,
∴AF=BF,即CD垂直平分AB,
∴CA=CB=3,
∵AO⊥BC,
∴CE=BE,即AE垂直平分BC,
∴AB=AC=3;
(2)∵AB=AC=BC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴AE⊥BC,
∴AE平分∠BAC,即∠OAF=30°,
在Rt△OAF中,∵OF=AF=×=,
∴OA=2OF=,
即⊙O的半径为.
7.解:(1)连接AC,如图1所示:∵AH⊥BC,
∴∠AHB=∠AHC=90°,
∴BH===4,
∴CH=BC﹣BH=4,
∴CA==5,
当⊙C经过点A时,CP=CA=5;
(2)∵四边形ABCD是平行四边形,
∴AD∥BC,当AP∥CE时,四边形APCE是平行四边形,
∵CP=CE,
∴四边形APCE是菱形,
∴PA=CP,
设PA=CP=x,则PH=4﹣x,
在Rt△APH中,
由勾股定理得:AH2+PH2=PA2,
即32+(4﹣x)2=x2,
解得:x=,
即⊙C的半径为,
作CM⊥EF于M,如图2所示:则CM=AH=3,ME=MF=EF,
在Rt△CEM中,由勾股定理得:ME===,
∴EF=2ME=.
8.(1)证明:∵AD=DC,
∴=,
∴OD⊥AC,
∴∠AEO=90°,
∵AB是直径,
∴∠ACB=90°,
∴∠AEO=∠ACB,
∴OD∥BC.
(2)解:∵OD⊥AC,
∴AE=EC=5,
设OA=OD=r,
在Rt△AOE中,OA2=AE2+OE2,
∴r2=52+(r﹣4)2,
∴r=,
∴OE=r﹣DE=﹣4=,
∵AE=EC,AO=OB,
∴BC=2OE=.
9.解:(1)过点O作OH⊥EF于H,
由勾股定理得,AC==4,
∵DE⊥AD,∠ACB=90°,
∴∠ACB=∠ADE,
∵∠C=∠C,
∴△ACB∽△ADE,
∴=,即=,
解得,DE=6,
∴⊙O的半径为3,
AE==10,
∵∠EHO=∠EDA,∠OEH=∠AED,
∴△EHO∽△EDA,
∴=,即=,
解得,OH=,
∴点O到EF距离为;
(2)连接EG,
∵AE=10,AC=4,
∴EC=6,
∴EC=ED,
∵DE是⊙O的直径,
∴EG⊥CD,
∴G是CD的中点.
10.解:(1)∵OA=OB,
∴∠OAB=∠OBA,
∵AB∥CD,
∴∠C=∠OAB,∠D=∠OBA,
∴∠C=∠D,
∴OD=OC=OA+AC=5+3=8;
(2)过O点作OE⊥MN于E,连接OM,如图,则ME=NE,
在Rt△OCE中,tanC==,
设OE=3x,则CE=4x,
∴OC=5x,
即5x=8,解得x=,
∴OE=,
在Rt△OME中,ME===,
∴MN=2ME=.
11.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG.
(2)解:设⊙O的半径为r.则AG=OA+OG=r+10,
∵CA=CG,CD⊥AB,
∴AE=EG=,EC=ED=4,
∴OE=AE﹣OA=,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=()2+42,
解得r=或(舍弃),
∴⊙O的半径为.
12.(1)解:连接OA交BF于G,如图,⊙O的半径为r,
∵AD⊥OB,
∴AH=DH=4,
在Rt△OHA中,OH=r﹣2,OA=r,
∴r2=42+(r﹣2)2
,解得r=5,
即⊙O的半径为5;
(2)方法一
证明:连接CF,如图,
∵AD⊥OB,
∴弧AB=弧DB,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴OA⊥BG,
∴BG=FG,
∴∠OAH=∠OBG,
在△OAH和△OBG中,
,
∴△OAH≌△OBG(AAS),
∴AH=BG,
∴BF=2AH.
方法二:∵AD⊥OB,
∴弧AB=弧DB,AH=DH,
∵∠EAB=∠EBA,
∴弧BD=弧AF,
∴弧AB=弧AF,
∴弧AD=弧BF,
∴BF=AD=2AH.
13.解:(1)如图(一),过M作MT⊥BC于T连BM,
∵BC是⊙M的一条弦,MT是垂直于BC的直径,
∴BT=TC=BC=2,
∴BM==4;
(2)如图(二),连接AE,则∠AEC=∠ABC,
∵CE⊥AB,
∴∠HBC+∠BCH=90°
在△COF中,
∵∠OFC+∠OCF=90°,
∴∠HBC=∠OFC=∠AFH.
在△AEH和△AFH中,
∵,
∴△AEH≌△AFH(AAS),
∴EH=FH.
(3)由(1)易知,∠BMT=∠BAC=60°,
作直径BG,连CG,则∠BGC=∠BAC=60°,
∵⊙O的半径为4,
∴CG=4.
连AG,
∵∠BCG=90°,
∴CG⊥x轴,
∴CG∥AF,
∵∠BAG=90°,
∴AG⊥AB,
∵CE⊥AB,
∴AG∥CE,
∴四边形AFCG为口,
∴AF=CG=4.
14.解:(1)作AE⊥BC于E,如图1所示:
则AE=DC,EC=AD=2,
∴BE=BC﹣EC=9﹣2=7,
∴CD=AE===4,
∴AC===6;
(2)作BF⊥AC于F,连接OA,如图2所示:
则AF=CF=AC=3,
∴BF垂直平分AC,
∴BF一定过圆心O,BF===6,
设⊙O的半径为r,则OF=6﹣r,
在Rt△OAF中,由勾股定理得:(6﹣r)2+32=r2,
解得:r=,
即⊙O的半径为.
15.解:(1)连接AC,∵AB∥CD且AE⊥CD,
∴AB⊥AE,∠ECA=∠BAC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠B+∠BAC=∠BAC+∠EAC=90°,
∴∠B=∠EAC,
∵∠ADE=∠B,
∴∠EAC=∠ADE,
∵∠E=∠AEC,
∴△ACE∽△DAE,
∴=,
∴AE2=ED EC,
设DE=x,则22=x(x+3),
解得:x1=1,x2=﹣4(舍去),
即:DE=1,
在Rt△ACE中,AC2=AE2+CE2,
∴AC2=20,
∵∠ACB=∠E,∠CAE=∠B,
∴△ACE∽△BAC,
∴=
∴AB=5;
(2)设BE与PQ交于G,AB与PQ交于F,
∵AE=2,AB=5,
∴BE==,
∵翻折使点B与E重合,
∴BG⊥PQ,BG=BE=,
∵∠BGF=∠EAB=90°,∠GBF=∠ABE,
∴△BGF∽△BAE,
∴=,
∴=,
∴BF=,
∴OF=﹣=,
过O作OH⊥于H,
∴OH∥BG,PQ=2HQ,
∴△OFH∽△BFG,
∴=,
∴=,
∴OH=,
连接OQ,
∴HQ==,
∴PQ=2HQ=,
∴△BPQ的面积=×=.
16.解:如图,连接AD,AC,连接CD与AB交于点F,
∵AB⊥BC,
∴∠ABC=90°.
∴AC为直径.
∴∠ADC=90°.
∵AE=DE,DE⊥AB,
∴∠DAB=∠ADE=45°.
∴∠BCF=∠DAB=45°.
∴BC=BF=3.
在△ADF中,∠DAB=∠AFD=45°,
∴EF=ED=1.
∴AB=5.
∴AC==.
∴⊙O半径的长.
17.解:(1)如图1中,连接OB,OC.设BF=EF=x,OF=y.
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∴∠CEF=∠BFO=90°
∴AF=BF=x,DE=EC=2,
根据勾股定理可得:,
解得(舍弃)或,
∴BF=4,AB=2BF=8.
(2)如图2中,作CH⊥AB于H.
∵OB⊥OC,
∴∠A=∠BOC=45°,
∵AH⊥CH,
∴△ACH是等腰直角三角形,
∵AC=CH,
∵AB∥CD,EF⊥AB,
∴EF⊥CD,
∠CEF=∠EFH=∠CHF=90°,
∴四边形EFHC是矩形,
∴CH=EF,
在Rt△OEC中,∵EC=,OC=,
OE===2,
∵∠EOC+∠OCE=90°,∠EOC+∠FOB=90°,
∴∠FOB=∠ECO,
∵OB=OC,
∴△OFB≌△CEO(AAS),
∴OF=EC=,
∴CH=EF=3,
∴AC=EF=6.
18.解:(1)如图1,设∠BDC=α,∠DAC=β,
则∠CAB=∠BDC=α,
∵点C为弧ABD中点,
∴=,
∴∠ADC=∠DAC=β,
∴∠DAB=β﹣α,
连接AD,
∵AB为⊙O直径,
∴∠ADB=90°,
∴α+β=90°,
∴β=90°﹣α,
∴∠ABD=90°﹣∠DAB=90°﹣(β﹣α),
∴∠ABD=2α,
∴∠ABD=2∠BDC;
(2)∵CE⊥AB,
∴∠ACE+∠CAB=∠ADC+∠BDC=90°,
∵∠CAB=∠CDB,
∴∠ACE=∠ADC,
∵∠CAE=∠ADC,
∴∠ACE=∠CAE,
∴AE=CE;
(3)如图2,连接OC,
∴∠COB=2∠CAB,
∵∠ABD=2∠BDC,∠BDC=∠CAB,
∴∠COB=∠ABD,
∵∠OHC=∠ADB=90°,
∴△OCH∽△ABD,
∴,
∵OH=5,
∴BD=10,
∴AB==26,
∴AO=13,
∴AH=18,
∵△AHE∽△ADB,
∴,即=,
∴AE=,
∴DE=.
19.解:(1)作CH⊥MN于H,则H为MN的中点,
∵OB=1+,OC=
∴CB=1
又∵∠ABC=45°
∴CH=
连接CM、CN,在Rt△HCM中,
∵CH=,
又∵MC=
∴MH=,
∴MN=
(2)在Rt△MCH中,
∵CH=,
又∵MC=
∴∠MCH=60°
∴∠MCN=120°
∴∠MON=60°.
20.(1)证明:∵PD∥CB,∴=,∴∠FBC=∠FCB,∴FC=FB.
(2)解:如图:连接OC,设圆的半径为r,在Rt△OCE中,
OC=r,OE=r﹣8,CE=12,∴r2=(r﹣8)2+122,
解方程得:r=13.
所以⊙O的直径为26.
