2021-2022学年北师大版九年级数学下册3.5确定圆的条件 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.5确定圆的条件 解答题专题提升训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 624.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3-5确定圆的条件》
解答题专题提升训练(附答案)
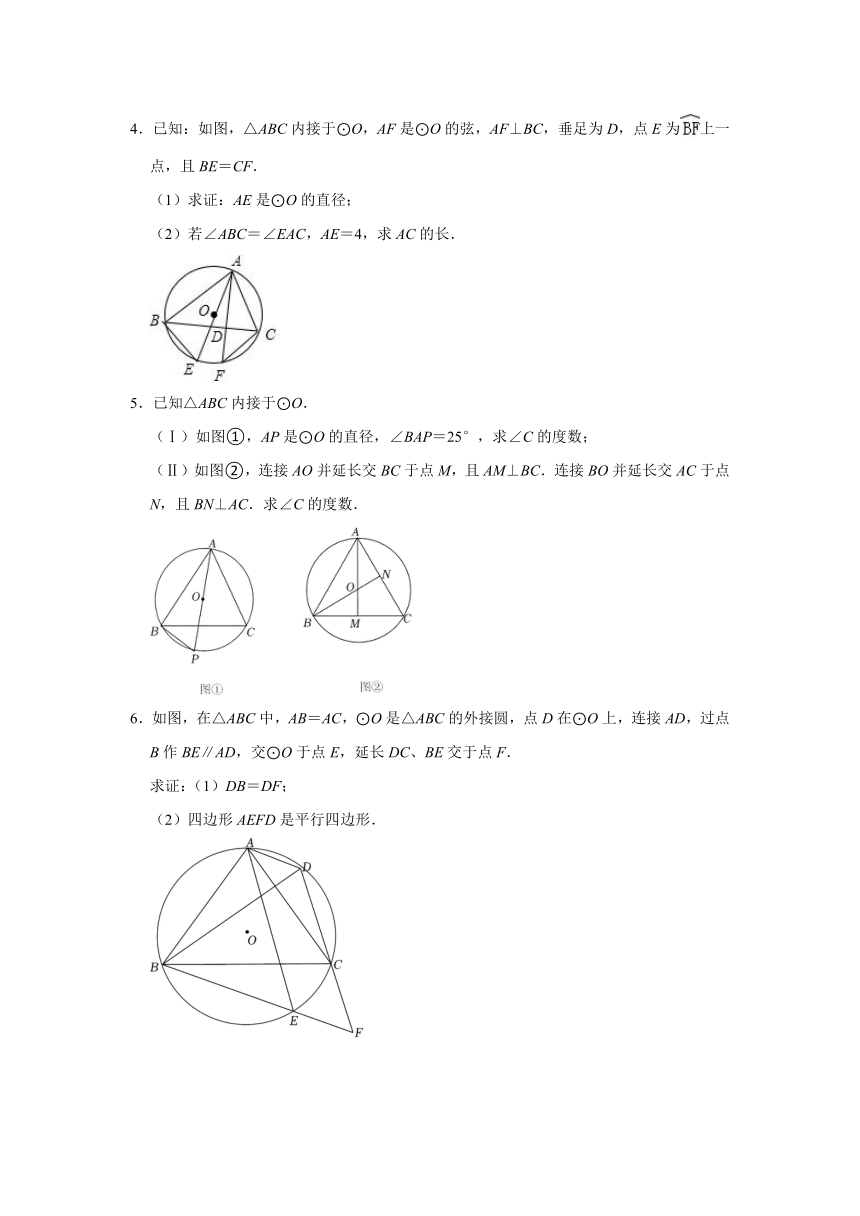
1.如图,D是等腰三角形ABC底边的中点,过点A、B、D作⊙O.
(1)求证:AB是⊙O的直径;
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE.
2.已知如图,△ABC内接于⊙O,AE为直径,AD⊥BC于点D,EF⊥BC于点F.
(1)求证:∠DAC=∠BAE;
(2)当点C是的中点时,求证:FC=AD.
3.已知△ABC是⊙O的内接三角形,∠ACB的平分线交⊙O于点D.
(Ⅰ)如图1,若AB是⊙O的直径,AB=6,求AD的长;
(Ⅱ)如图2,若∠BAC的平分线交CD于点E,求证:DE=DA.
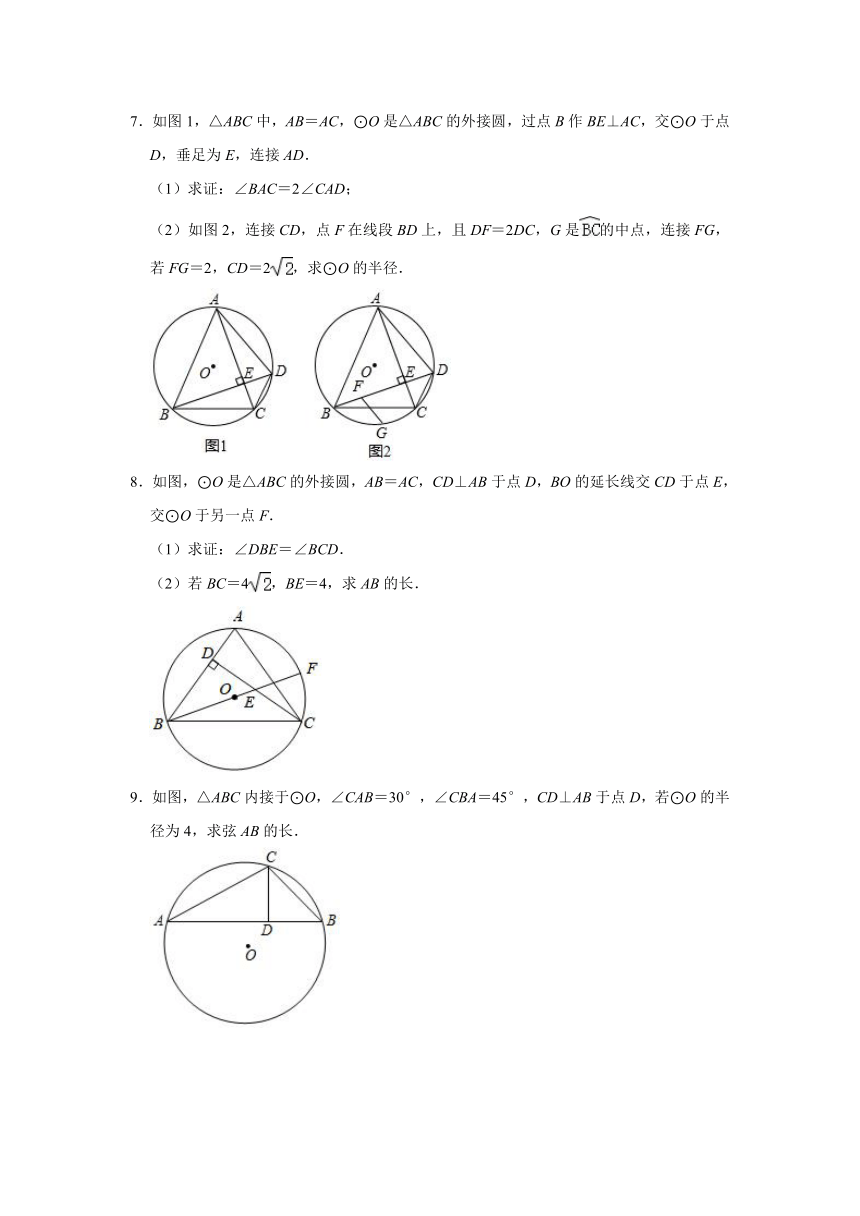
4.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为上一点,且BE=CF.
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=4,求AC的长.
5.已知△ABC内接于⊙O.
(Ⅰ)如图①,AP是⊙O的直径,∠BAP=25°,求∠C的度数;
(Ⅱ)如图②,连接AO并延长交BC于点M,且AM⊥BC.连接BO并延长交AC于点N,且BN⊥AC.求∠C的度数.
6.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,点D在⊙O上,连接AD,过点B作BE∥AD,交⊙O于点E,延长DC、BE交于点F.
求证:(1)DB=DF;
(2)四边形AEFD是平行四边形.
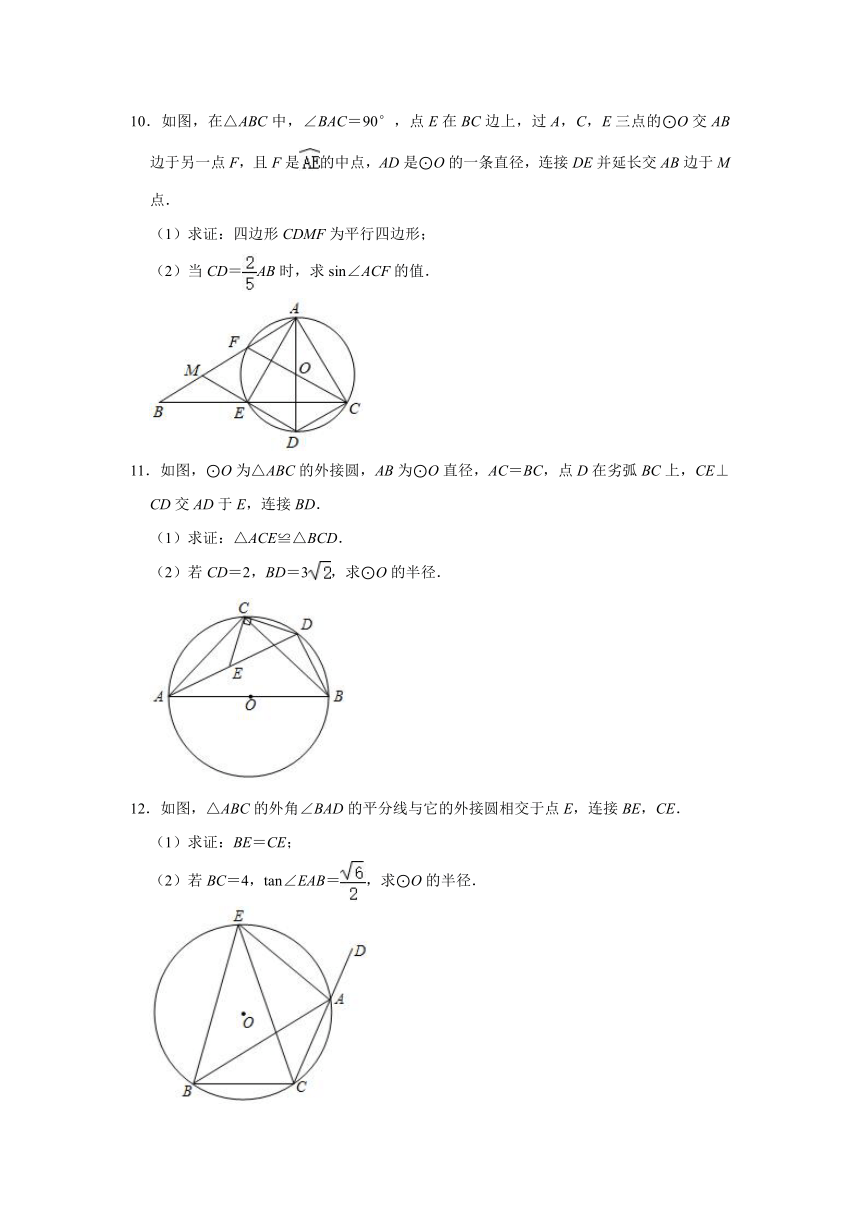
7.如图1,△ABC中,AB=AC,⊙O是△ABC的外接圆,过点B作BE⊥AC,交⊙O于点D,垂足为E,连接AD.
(1)求证:∠BAC=2∠CAD;
(2)如图2,连接CD,点F在线段BD上,且DF=2DC,G是的中点,连接FG,若FG=2,CD=2,求⊙O的半径.
8.如图,⊙O是△ABC的外接圆,AB=AC,CD⊥AB于点D,BO的延长线交CD于点E,交⊙O于另一点F.
(1)求证:∠DBE=∠BCD.
(2)若BC=4,BE=4,求AB的长.
9.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为4,求弦AB的长.
10.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
11.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
12.如图,△ABC的外角∠BAD的平分线与它的外接圆相交于点E,连接BE,CE.
(1)求证:BE=CE;
(2)若BC=4,tan∠EAB=,求⊙O的半径.
13.如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AC=2DH,∠COD=23°,求∠P的度数.
14.如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连接EF并延长交AC于点G,连接BE,BD,四边形BDGE是平行四边形.
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
15.材料:如图①,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是弧ABC的中点,则从点M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
(1)如图②,已知等边△ABC内接于⊙O,AB=12,D为弧AC上一点,∠ABD=45°,AE⊥BD于点E,求△BDC的周长;
(2)求证:CD=AB+BD.
16.如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.
(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
17.如图,Rt△ABC中,∠C=90°,M为AB上一点,过M,C,B三点的⊙O交AC于P,过点P作PD∥AB,交⊙O于点D.
(1)若M是AB中点,连接MD,求证:四边形APDM是平行四边形;
(2)连接PM,当PM=PC,且AC=4,tanA=,求线段PD的长.
18.如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
19.如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C),过A,C,D三点的⊙O交AB于另一点E,连接AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连接EF.
(1)求证:四边形DCFE是菱形;
(2)当tan∠AEF=,AC=4时,求⊙O的直径长.
20.如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=DH,∠OHD=80°,求∠BDE的大小.
参考答案
1.(1)证明:连接BD,
∵BA=BC,AD=DC,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(2)证明:∵BA=BC,
∴∠A=∠C,
由圆周角定理得,∠A=∠E,
∴∠C=∠E,
∴DC=DE.
2.证明:(1)连接BE,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴∠AEB+∠BAE=90°,
∵AD⊥BC,
∴∠ACB+∠DAC=90°,
由圆周角定理得:∠AEB=∠ACB,
∴∠DAC=∠BAE;
(2)连接CE,
∵点C是的中点,
∴=,
∴AC=CE,
∵∠DAC=∠BAE,∠FCE=∠BAE,
∴∠DAC=∠FCE,
在△CFE和△ADC中,
,
∴△CFE≌△ADC(AAS),
∴FC=AD.
3.(Ⅰ)解:连接OD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴,
∴∠AOD=90°,
即△AOD为等腰直角三角形,
∵AB=6,
∴OA=OD=3.
∴;
(Ⅱ)证明:∵AE平分∠BAC,
∴∠CAE=∠EAB,
∵∠BCD=∠BAD,
∠ACD=∠BCD,
∴∠ACD=∠BAD,
∴∠ACD+∠CAE=∠BAD+∠EAB,
即∠EAD=∠AED,
∴DE=DA.
4.(1)证明:∵BE=CF,
∴=,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴∠CAF+∠ACB=90°,
由圆周角定理得:∠ACB=∠AEB,
∴∠BAE+∠AEB=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)解:连接CE,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵∠ABC=∠EAC,
∴=,
∴AC=CE,
∴AC=AE=2.
5.解:(1)∵AP为直径,
∴∠ABP=90°,
∴∠APB=90°﹣∠BAP=65°,
∴∠C=∠APB=25°.
(2)∵AM⊥BC,
∴点M为BC中点,
∴AB=AC,
∵BN⊥AC,
∴点N为AC中点,
∴AB=BC,
∴AB=AC=BC,即△ABC为等边三角形,
∴∠C=60°.
6.证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
由圆周角定理得:∠ADB=∠ACB,
∴∠ABC=∠ADB,
∵BE∥AD,
∴∠ADB=∠DBF,∠DFB+∠ADC=180°,
∴∠ABC=∠DBF,
∵四边形ABCD为⊙O的内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC=∠DFB,
∴∠DFB=∠DBF,
∴DB=DF;
(2)由圆周角定理得:∠ADB=∠AEB,
∴∠DBF=∠AEB,
∴∠AEB=∠DFB,
∴AE∥CD,
∵BE∥AD,
∴四边形AEFD是平行四边形.
7.(1)证明:如图1,作AH⊥BC于H,
∴∠AHC=90°,
∴∠HAC+∠C=90°,
∵AB=AC,
∴∠BAC=2∠CAH,
∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠C=90°,
∴∠CBE=∠CAH,
∵=,
∴∠CAD=∠CBE,
∴∠CAH=∠CAD,
∴∠BAC=2∠CAD;
(2)解:如图,连接GC并延长交AD延长线于点H,连接DG,BG,AG,
∵G是的中点,
∴,
∴GB=GC,∠BAG=∠CAG,
∴∠CAG=∠DAC,
∵AB=AC,
∴AG垂直平分BC,
∴AG为直径,
∴∠ADG=∠ACG=90°,
∴∠GDH=∠ACH=90°,
∵∠AGC+∠CAG=90°,∠AHC+∠CAH=90°,
∴∠AGC=∠AHC,
∴AG=AH,
∴CG=CH,
在Rt△GDH中,DC=CG=CH,即GH=2DC=DF,
∵∠AEB=90°=∠ACG,
∴BD∥GH,
∴四边形GHDF为平行四边形,
∴DH=FG=2,
设半径为r,则AH=AG=2r,AD=2r﹣2,
在Rt△AGD中,DG2=AG2﹣AD2=(2r)2﹣(2r﹣2)2=8r﹣4,
在Rt△GDH中,GH=DF=2CD=4,
∴DG2=GH2﹣DH2=32﹣4=28,
∴8r﹣4=28,解得r=4,
∴⊙O的半径为4.
8.(1)证明:如图,连接CF,
∵BF为直径,
∴∠BCF=90°,
∵CD⊥AB,
∴∠ADC=90°,
∵∠BAC=∠BFC,
∴∠ACD=180°﹣∠ADC﹣∠BAC,
∠FBC=180°﹣∠BCF﹣∠BFC,
∴∠ACD=∠FBC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DBE=∠BCD;
(2)解:∠DBE+∠DEB=90°,∠DEB=∠FEC,
∴∠DBE+∠FEC=90°,
∵∠BCD+∠FCE=90°,∠DBE=∠BCD,
∴∠FEC=∠FCE,
∴FE=FC,
设FC=x,则BF=4+x,
在Rt△BCF中,BC2+FC2=BF2,即(4)2+x2=(4+x)2,
解得x=2,
∴BF=6,
如图,过点A作AG⊥BC于G,
∵AB=AC,
∴BG=CG=2,
∴点A、O、G在同一直线上,
∴OG=FC=1,
∴AG=AO+OG=4,
在Rt△ABG中,AB2=AG2+BG2=24,
∴AB=2.
9.解:如图,连接OA,OC.
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,根据勾股定理得:AC==4,
∵CD⊥AB,∠CAB=30°,
∴CD=BD=AC=2.
∴AD=CD=2,
∴AB=AD+BD=2+2.
10.(1)证明:连接DF、EF,
∵∠BAC=90°,
∴FC是⊙O的直径,
∵F是的中点,
∴=,
∴∠ADF=∠EDF,
∵OF=OD,
∴∠ADF=∠OFD,
∴∠OFD=∠EDF,
∴FC∥DM,
∵OA=OD,OF=OC,∠BAC=90°,
∴四边形AFDC为矩形,
∴AF∥CD,
∴四边形CDMF为平行四边形;
(2)解:∵四边形AFDC为矩形,四边形CDMF为平行四边形,
∴CD=AF=FM=EF,
∵CD=AB,
∴CD=(2CD+BM),
∴CD=2BM,
∵BM∥CD,
∴△BEM∽△CED,
∴==,
∴EC=2BE,
设BM=a,则CD=2a,BF=3a,EF=2a,
在Rt△BEF中,BE==a,
∴EC=2a,
在Rt△CEF中,FC==2a,
在Rt△FAC中,sin∠ACF===.
11.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
12.(1)证明:∵四边形ACBE是圆内接四边形,
∴∠EAD=∠EBC,
∵AE平分∠BAD,
∴∠EAD=∠BAE,
∴∠BAE=∠EBC,
∴BE=CE.
(2)解:如图,连接EO并延长交BC于点F,连接OB,
由圆的对称性及等腰三角形的对称性可知,EF⊥BC,
∴点F是BC的中点,
∵BC=4,tan∠EAB=,
∴BF=2,tan∠EAB==,
∴EF=,
设⊙O的半径的半径为r,
∴OE=OB=r,OF=﹣r,
∴OF2+BF2=OB2,即(﹣r)2+22=r2,
解得,r=.
13.(1)证明:如图1,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:∵PC=PB,
∴∠PCB=∠PBC,
由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
∵AC=2DH,
∴AC=2BC,
在Rt△ABC中,
∵AB==BC,
∴tan∠ACB==,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=(180°﹣23°)=( )°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=( )°,
∵PC=PB,
∴∠P=180°﹣2×( )°=97°.
14.解:(1)连接AF,
∵AE是⊙O的直径,
∴AF⊥EG,
∵四边形BDGE是平行四边形,
∴BD∥EG,
∴BD⊥AF,
∵∠BAC=90°,
∴BD是⊙O的直径,
∴BD垂直平分AF,
∴AB=BF;
(2)∵当F为BC的中点,
∴BF=BC,
∵AB=BF,
∴AB=BC,
∵∠BAC=90°,
∴∠C=30°,
∴∠ABC=60°,AB=AC=,
∵AB=BF,
∴∠ABD=30°,
∴BD=2,
∴⊙O的直径长为2.
15.(1)解:∵AE⊥BD,∠ABD=45°,
∴△AEB是等腰直角三角形,
∴BE==6,
∵△ABC是等边三角形,
∴AB=AC,
∴点A为弧BDC的中点,
∴AE平分折弦CDB,即BE=ED+DC,
∴BD+DC=2BE=12,
∴△BDC的周长=BD+CD+BC=12+12;
(2)证明:如图,在CB上截取CG=AB,连接MA,MB,MC和MG,
∵M是弧ABC的中点,
∴MA=MC,
∵BA=GC,∠A=∠C,MA=MC,
∴△MBA≌△MGC(SAS),
∴MB=MG,
∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD.
16.解:(1)∵△ABC为等边三角形,
∴AB=BC,
∴∠ABD=∠∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BDA=∠CEB,
∵∠CEB=∠F+∠FCE,
∵∠F=∠BAC=∠BCA=60°,
∴∠CEB=∠BCA+∠FCE=∠BCF,
∴∠BDA=∠BCF,
∴AD∥CF;
(2)如图,连接PC,
当△PEC为直角三角形时,可分3种情况讨论:
①∠PCE=90°或∠CEP=90°或∠CPE=90°,
①当∠PCE=90°时,
∵∠PCE<∠ACB=60°,
∴∠PCE=90°这种情况不存在;
②当∠PEC=90°时,
∵∠PEC=∠F+∠ACF,
∵∠F=60°,
∴∠ACF=30°,
∴tan∠ACF=;
③当∠CPE=90°时,过点A作AH⊥BC于点H,如图,
设AE=x,则CD=AE=x,CE=6﹣x,
∵AB=AC,AH⊥BC,
∴BH=CH=3,∠HAC=∠HAB=30°,
∴HD=3﹣x,
∵∠BFC=60°,∠CPE=90°,
∴∠PCF=∠HAC=30°,
∴AD∥FC,
∴∠FCA=∠DAC,
∴∠PCF﹣∠FCA=∠HAC﹣∠DAC,
∴∠HAD=∠PCE,
∵∠AHD=∠CPE=90°,
∴△AHD∽△CPE,
∴=,
∴PE AD=HD CE①,
∵∠BPD=∠APE=∠ACB=60°,
∠PAE=∠CAD,
∴△PAE∽△CAD,
∴PE AD=AE CD②,
观察①②式可知:
HD CE=AE CD,
∴(3﹣x)(6﹣x)=x2,
解得x=2,
∴AE=2,
过点E作EG⊥AB于点G,
在Rt△AEG中,∠EAG=60°,
∴AG=AE cos60°=2×=1,
EG=AE sin60°=2×=,
∴BG=AB﹣AG=6﹣1=5,
在Rt△BGE中,tan∠ABE==,
∴tan∠ACF=tan∠ABE=,
综上所述,当△PEC为直角三角形时,
tan∠ACF的值为或.
17.(1)证明:连接CM,PB,DM,如图1所示:
∵∠C=90°,四边形BCPM为圆内接四边形,
∴∠C+∠BMP=180°,
∴∠BMP=90°,BP为⊙O的直径,
又∵PD∥AB,
∴∠DPM=180°﹣∠BMP=90°,
∴MD为⊙O的直径,
∵∠C=90°,M为AB的中点,
∴CM=AB=BM,
∴,
又∵MD为⊙O的直径,
∴DM垂直平分BC,
∴PC∥MD,
∴四边形APDM为平行四边形;
(2)解:连接BD、CD、BP,如图2所示:
∵MD和BP均为⊙O的直径,
∴∠DPM=∠PMB=∠PDB=90°,
∴四边形PDBM为矩形,
∴PM=BD,
∵PM=PC,
∴PC=BD,
在Rt△BPD和Rt△PBC中,,
∴Rt△BPD≌Rt△PBC(HL),
∴PD=BC,
在Rt△ACB中,AC=4,tanA==,
∴BC=4tanA=2,
∴PD=BC=2.
18.(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴=,即=,
解得,AF=.
19.解:(1)证明:∵CE⊥AD,
∴EG=CG,
∵CF∥DE,
∴∠DEG=∠FCG,
∵∠FGC=∠DGE,
∴△DEG≌△FCG(ASA),
∴ED=FC,
∴四边形DCFE为平行四边形,
又∵CE⊥DF,
∴四边形DCFE是菱形;
(2)∵AG⊥EC,EG=CG,
∴AE=AC=4,
∵四边形AEDC内接于⊙O,
∴∠BED=∠BCA=90°,
∵四边形DCFE是菱形,
∴EF∥DC,DE=DC,
∴∠AEF=∠ABC,
∴tan∠ABC=tan∠AEF=,
在Rt△BED中,设DE=3a,则BE=4a,
∴DC=3a,BD==5a,
∵BC2+AC2=AB2,
∴(5a+3a)2+42=(4a+4)2,
解得a=或a=0(舍去),
∴DE=DC=2,
∴AD===2.
即⊙O的直径长为2.
20.(1)证明:如图1,∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(2)由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,∵AB=DH,
∴tan∠ACB==,
∴∠ACB=60°,∠BAC=30°,
∴∠ADB=60°,BC=AC,
∴DH=AC,
①当点O在DE的左侧时,如图2,作直径DM,连接AM、OH,则∠DAM=90°,
∴∠AMD+∠ADM=90°
∵DE⊥AB,
∴∠BED=90°,
∴∠BDE+∠ABD=90°,
∵∠AMD=∠ABD,
∴∠ADM=∠BDE,
∵DH=AC,
∴DH=OD,
∴∠DOH=∠OHD=80°,
∴∠ODH=20°
∵∠ADB=60°,
∴∠ADM+∠BDE=40°,
∴∠BDE=∠ADM=20°,
②当点O在DE的右侧时,如图3,作直径DN,连接BN,
由①得:∠ADE=∠BDN=20°,∠ODH=20°,
∴∠BDE=∠BDN+∠ODH=40°,
综上所述,∠BDE的度数为20°或40°.
解答题专题提升训练(附答案)
1.如图,D是等腰三角形ABC底边的中点,过点A、B、D作⊙O.
(1)求证:AB是⊙O的直径;
(2)延长CB交⊙O于点E,连接DE,求证:DC=DE.
2.已知如图,△ABC内接于⊙O,AE为直径,AD⊥BC于点D,EF⊥BC于点F.
(1)求证:∠DAC=∠BAE;
(2)当点C是的中点时,求证:FC=AD.
3.已知△ABC是⊙O的内接三角形,∠ACB的平分线交⊙O于点D.
(Ⅰ)如图1,若AB是⊙O的直径,AB=6,求AD的长;
(Ⅱ)如图2,若∠BAC的平分线交CD于点E,求证:DE=DA.
4.已知:如图,△ABC内接于⊙O,AF是⊙O的弦,AF⊥BC,垂足为D,点E为上一点,且BE=CF.
(1)求证:AE是⊙O的直径;
(2)若∠ABC=∠EAC,AE=4,求AC的长.
5.已知△ABC内接于⊙O.
(Ⅰ)如图①,AP是⊙O的直径,∠BAP=25°,求∠C的度数;
(Ⅱ)如图②,连接AO并延长交BC于点M,且AM⊥BC.连接BO并延长交AC于点N,且BN⊥AC.求∠C的度数.
6.如图,在△ABC中,AB=AC,⊙O是△ABC的外接圆,点D在⊙O上,连接AD,过点B作BE∥AD,交⊙O于点E,延长DC、BE交于点F.
求证:(1)DB=DF;
(2)四边形AEFD是平行四边形.
7.如图1,△ABC中,AB=AC,⊙O是△ABC的外接圆,过点B作BE⊥AC,交⊙O于点D,垂足为E,连接AD.
(1)求证:∠BAC=2∠CAD;
(2)如图2,连接CD,点F在线段BD上,且DF=2DC,G是的中点,连接FG,若FG=2,CD=2,求⊙O的半径.
8.如图,⊙O是△ABC的外接圆,AB=AC,CD⊥AB于点D,BO的延长线交CD于点E,交⊙O于另一点F.
(1)求证:∠DBE=∠BCD.
(2)若BC=4,BE=4,求AB的长.
9.如图,△ABC内接于⊙O,∠CAB=30°,∠CBA=45°,CD⊥AB于点D,若⊙O的半径为4,求弦AB的长.
10.如图,在△ABC中,∠BAC=90°,点E在BC边上,过A,C,E三点的⊙O交AB边于另一点F,且F是的中点,AD是⊙O的一条直径,连接DE并延长交AB边于M点.
(1)求证:四边形CDMF为平行四边形;
(2)当CD=AB时,求sin∠ACF的值.
11.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.
(1)求证:△ACE≌△BCD.
(2)若CD=2,BD=3,求⊙O的半径.
12.如图,△ABC的外角∠BAD的平分线与它的外接圆相交于点E,连接BE,CE.
(1)求证:BE=CE;
(2)若BC=4,tan∠EAB=,求⊙O的半径.
13.如图,D是△ABC外接圆上的点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:∠BAD=∠PCB;
(2)求证:BG∥CD;
(3)设△ABC外接圆的圆心为O,若AC=2DH,∠COD=23°,求∠P的度数.
14.如图,在△ABC中,∠BAC=90°,点F在BC边上,过A,B,F三点的⊙O交AC于另一点D,作直径AE,连接EF并延长交AC于点G,连接BE,BD,四边形BDGE是平行四边形.
(1)求证:AB=BF.
(2)当F为BC的中点,且AC=3时,求⊙O的直径长.
15.材料:如图①,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是弧ABC的中点,则从点M向BC所作垂线的垂足D是折弦ABC的中点,即CD=AB+BD.
(1)如图②,已知等边△ABC内接于⊙O,AB=12,D为弧AC上一点,∠ABD=45°,AE⊥BD于点E,求△BDC的周长;
(2)求证:CD=AB+BD.
16.如图,已知⊙O是边长为6的等边△ABC的外接圆,点D,E分别是BC,AC上两点,且BD=CE,连接AD,BE相交于点P,延长线段BE交⊙O于点F,连接CF.
(1)求证:AD∥FC;
(2)连接PC,当△PEC为直角三角形时,求tan∠ACF的值.
17.如图,Rt△ABC中,∠C=90°,M为AB上一点,过M,C,B三点的⊙O交AC于P,过点P作PD∥AB,交⊙O于点D.
(1)若M是AB中点,连接MD,求证:四边形APDM是平行四边形;
(2)连接PM,当PM=PC,且AC=4,tanA=,求线段PD的长.
18.如图,△ABC是⊙O的内接三角形.AE是⊙O的直径,交BC于点G.过点A作AF⊥BC,AF分别与BC、⊙O交于点D、F,连接BE、CF.
(1)求证:∠BAE=∠CAF;
(2)若AB=8,AC=6,AG=5,求AF的长.
19.如图,在△ABC中,∠ACB=90°,点D在BC边上(不包括端点B,C),过A,C,D三点的⊙O交AB于另一点E,连接AD,DE,CE,且CE⊥AD于点G,过点C作CF∥DE交AD于点F,连接EF.
(1)求证:四边形DCFE是菱形;
(2)当tan∠AEF=,AC=4时,求⊙O的直径长.
20.如图,D是△ABC外接圆上的动点,且B,D位于AC的两侧,DE⊥AB,垂足为E,DE的延长线交此圆于点F.BG⊥AD,垂足为G,BG交DE于点H,DC,FB的延长线交于点P,且PC=PB.
(1)求证:BG∥CD;
(2)设△ABC外接圆的圆心为O,若AB=DH,∠OHD=80°,求∠BDE的大小.
参考答案
1.(1)证明:连接BD,
∵BA=BC,AD=DC,
∴BD⊥AC,
∴∠ADB=90°,
∴AB是⊙O的直径;
(2)证明:∵BA=BC,
∴∠A=∠C,
由圆周角定理得,∠A=∠E,
∴∠C=∠E,
∴DC=DE.
2.证明:(1)连接BE,
∵AE为⊙O的直径,
∴∠ABE=90°,
∴∠AEB+∠BAE=90°,
∵AD⊥BC,
∴∠ACB+∠DAC=90°,
由圆周角定理得:∠AEB=∠ACB,
∴∠DAC=∠BAE;
(2)连接CE,
∵点C是的中点,
∴=,
∴AC=CE,
∵∠DAC=∠BAE,∠FCE=∠BAE,
∴∠DAC=∠FCE,
在△CFE和△ADC中,
,
∴△CFE≌△ADC(AAS),
∴FC=AD.
3.(Ⅰ)解:连接OD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵CD平分∠ACB,
∴,
∴∠AOD=90°,
即△AOD为等腰直角三角形,
∵AB=6,
∴OA=OD=3.
∴;
(Ⅱ)证明:∵AE平分∠BAC,
∴∠CAE=∠EAB,
∵∠BCD=∠BAD,
∠ACD=∠BCD,
∴∠ACD=∠BAD,
∴∠ACD+∠CAE=∠BAD+∠EAB,
即∠EAD=∠AED,
∴DE=DA.
4.(1)证明:∵BE=CF,
∴=,
∴∠BAE=∠CAF,
∵AF⊥BC,
∴∠CAF+∠ACB=90°,
由圆周角定理得:∠ACB=∠AEB,
∴∠BAE+∠AEB=90°,
∴∠ABE=90°,
∴AE是⊙O的直径;
(2)解:连接CE,
∵AE是⊙O的直径,
∴∠ACE=90°,
∵∠ABC=∠EAC,
∴=,
∴AC=CE,
∴AC=AE=2.
5.解:(1)∵AP为直径,
∴∠ABP=90°,
∴∠APB=90°﹣∠BAP=65°,
∴∠C=∠APB=25°.
(2)∵AM⊥BC,
∴点M为BC中点,
∴AB=AC,
∵BN⊥AC,
∴点N为AC中点,
∴AB=BC,
∴AB=AC=BC,即△ABC为等边三角形,
∴∠C=60°.
6.证明:(1)∵AB=AC,
∴∠ABC=∠ACB,
由圆周角定理得:∠ADB=∠ACB,
∴∠ABC=∠ADB,
∵BE∥AD,
∴∠ADB=∠DBF,∠DFB+∠ADC=180°,
∴∠ABC=∠DBF,
∵四边形ABCD为⊙O的内接四边形,
∴∠ABC+∠ADC=180°,
∴∠ABC=∠DFB,
∴∠DFB=∠DBF,
∴DB=DF;
(2)由圆周角定理得:∠ADB=∠AEB,
∴∠DBF=∠AEB,
∴∠AEB=∠DFB,
∴AE∥CD,
∵BE∥AD,
∴四边形AEFD是平行四边形.
7.(1)证明:如图1,作AH⊥BC于H,
∴∠AHC=90°,
∴∠HAC+∠C=90°,
∵AB=AC,
∴∠BAC=2∠CAH,
∵BE⊥AC,
∴∠BEC=90°,
∴∠CBE+∠C=90°,
∴∠CBE=∠CAH,
∵=,
∴∠CAD=∠CBE,
∴∠CAH=∠CAD,
∴∠BAC=2∠CAD;
(2)解:如图,连接GC并延长交AD延长线于点H,连接DG,BG,AG,
∵G是的中点,
∴,
∴GB=GC,∠BAG=∠CAG,
∴∠CAG=∠DAC,
∵AB=AC,
∴AG垂直平分BC,
∴AG为直径,
∴∠ADG=∠ACG=90°,
∴∠GDH=∠ACH=90°,
∵∠AGC+∠CAG=90°,∠AHC+∠CAH=90°,
∴∠AGC=∠AHC,
∴AG=AH,
∴CG=CH,
在Rt△GDH中,DC=CG=CH,即GH=2DC=DF,
∵∠AEB=90°=∠ACG,
∴BD∥GH,
∴四边形GHDF为平行四边形,
∴DH=FG=2,
设半径为r,则AH=AG=2r,AD=2r﹣2,
在Rt△AGD中,DG2=AG2﹣AD2=(2r)2﹣(2r﹣2)2=8r﹣4,
在Rt△GDH中,GH=DF=2CD=4,
∴DG2=GH2﹣DH2=32﹣4=28,
∴8r﹣4=28,解得r=4,
∴⊙O的半径为4.
8.(1)证明:如图,连接CF,
∵BF为直径,
∴∠BCF=90°,
∵CD⊥AB,
∴∠ADC=90°,
∵∠BAC=∠BFC,
∴∠ACD=180°﹣∠ADC﹣∠BAC,
∠FBC=180°﹣∠BCF﹣∠BFC,
∴∠ACD=∠FBC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠DBE=∠BCD;
(2)解:∠DBE+∠DEB=90°,∠DEB=∠FEC,
∴∠DBE+∠FEC=90°,
∵∠BCD+∠FCE=90°,∠DBE=∠BCD,
∴∠FEC=∠FCE,
∴FE=FC,
设FC=x,则BF=4+x,
在Rt△BCF中,BC2+FC2=BF2,即(4)2+x2=(4+x)2,
解得x=2,
∴BF=6,
如图,过点A作AG⊥BC于G,
∵AB=AC,
∴BG=CG=2,
∴点A、O、G在同一直线上,
∴OG=FC=1,
∴AG=AO+OG=4,
在Rt△ABG中,AB2=AG2+BG2=24,
∴AB=2.
9.解:如图,连接OA,OC.
∵∠COA=2∠CBA=2×45°=90°,
在Rt△AOC中,根据勾股定理得:AC==4,
∵CD⊥AB,∠CAB=30°,
∴CD=BD=AC=2.
∴AD=CD=2,
∴AB=AD+BD=2+2.
10.(1)证明:连接DF、EF,
∵∠BAC=90°,
∴FC是⊙O的直径,
∵F是的中点,
∴=,
∴∠ADF=∠EDF,
∵OF=OD,
∴∠ADF=∠OFD,
∴∠OFD=∠EDF,
∴FC∥DM,
∵OA=OD,OF=OC,∠BAC=90°,
∴四边形AFDC为矩形,
∴AF∥CD,
∴四边形CDMF为平行四边形;
(2)解:∵四边形AFDC为矩形,四边形CDMF为平行四边形,
∴CD=AF=FM=EF,
∵CD=AB,
∴CD=(2CD+BM),
∴CD=2BM,
∵BM∥CD,
∴△BEM∽△CED,
∴==,
∴EC=2BE,
设BM=a,则CD=2a,BF=3a,EF=2a,
在Rt△BEF中,BE==a,
∴EC=2a,
在Rt△CEF中,FC==2a,
在Rt△FAC中,sin∠ACF===.
11.解:(1)证明:∵AB为⊙O直径,
∴∠ACB=90°,
∵CE⊥CD,
∴∠ECD=90°,
∴∠ACE=90°﹣∠ECB=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(ASA);
(2)∵△ACE≌△BCD,
∴CE=CD,AE=BD,
∵CE⊥CD,
∴△ECD是等腰直角三角形,
∵CD=2,BD=3,
∴DE=2,AE=3,
∴AD=5,
∵AB为⊙O直径,
∴∠ADB=90°,
∴AB==2,
∴⊙O的半径为.
12.(1)证明:∵四边形ACBE是圆内接四边形,
∴∠EAD=∠EBC,
∵AE平分∠BAD,
∴∠EAD=∠BAE,
∴∠BAE=∠EBC,
∴BE=CE.
(2)解:如图,连接EO并延长交BC于点F,连接OB,
由圆的对称性及等腰三角形的对称性可知,EF⊥BC,
∴点F是BC的中点,
∵BC=4,tan∠EAB=,
∴BF=2,tan∠EAB==,
∴EF=,
设⊙O的半径的半径为r,
∴OE=OB=r,OF=﹣r,
∴OF2+BF2=OB2,即(﹣r)2+22=r2,
解得,r=.
13.(1)证明:如图1,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB;
(2)证明:∵PC=PB,
∴∠PCB=∠PBC,
由(1)得∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(3)解:由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
∵AC=2DH,
∴AC=2BC,
在Rt△ABC中,
∵AB==BC,
∴tan∠ACB==,
∴∠ACB=60°,
连接OD,
∵∠COD=23°,OD=OC,
∴∠OCD=(180°﹣23°)=( )°,
∴∠PCB=180°﹣∠ACB﹣∠OCD=( )°,
∵PC=PB,
∴∠P=180°﹣2×( )°=97°.
14.解:(1)连接AF,
∵AE是⊙O的直径,
∴AF⊥EG,
∵四边形BDGE是平行四边形,
∴BD∥EG,
∴BD⊥AF,
∵∠BAC=90°,
∴BD是⊙O的直径,
∴BD垂直平分AF,
∴AB=BF;
(2)∵当F为BC的中点,
∴BF=BC,
∵AB=BF,
∴AB=BC,
∵∠BAC=90°,
∴∠C=30°,
∴∠ABC=60°,AB=AC=,
∵AB=BF,
∴∠ABD=30°,
∴BD=2,
∴⊙O的直径长为2.
15.(1)解:∵AE⊥BD,∠ABD=45°,
∴△AEB是等腰直角三角形,
∴BE==6,
∵△ABC是等边三角形,
∴AB=AC,
∴点A为弧BDC的中点,
∴AE平分折弦CDB,即BE=ED+DC,
∴BD+DC=2BE=12,
∴△BDC的周长=BD+CD+BC=12+12;
(2)证明:如图,在CB上截取CG=AB,连接MA,MB,MC和MG,
∵M是弧ABC的中点,
∴MA=MC,
∵BA=GC,∠A=∠C,MA=MC,
∴△MBA≌△MGC(SAS),
∴MB=MG,
∵MD⊥BC,
∴BD=GD,
∴DC=GC+GD=AB+BD.
16.解:(1)∵△ABC为等边三角形,
∴AB=BC,
∴∠ABD=∠∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BDA=∠CEB,
∵∠CEB=∠F+∠FCE,
∵∠F=∠BAC=∠BCA=60°,
∴∠CEB=∠BCA+∠FCE=∠BCF,
∴∠BDA=∠BCF,
∴AD∥CF;
(2)如图,连接PC,
当△PEC为直角三角形时,可分3种情况讨论:
①∠PCE=90°或∠CEP=90°或∠CPE=90°,
①当∠PCE=90°时,
∵∠PCE<∠ACB=60°,
∴∠PCE=90°这种情况不存在;
②当∠PEC=90°时,
∵∠PEC=∠F+∠ACF,
∵∠F=60°,
∴∠ACF=30°,
∴tan∠ACF=;
③当∠CPE=90°时,过点A作AH⊥BC于点H,如图,
设AE=x,则CD=AE=x,CE=6﹣x,
∵AB=AC,AH⊥BC,
∴BH=CH=3,∠HAC=∠HAB=30°,
∴HD=3﹣x,
∵∠BFC=60°,∠CPE=90°,
∴∠PCF=∠HAC=30°,
∴AD∥FC,
∴∠FCA=∠DAC,
∴∠PCF﹣∠FCA=∠HAC﹣∠DAC,
∴∠HAD=∠PCE,
∵∠AHD=∠CPE=90°,
∴△AHD∽△CPE,
∴=,
∴PE AD=HD CE①,
∵∠BPD=∠APE=∠ACB=60°,
∠PAE=∠CAD,
∴△PAE∽△CAD,
∴PE AD=AE CD②,
观察①②式可知:
HD CE=AE CD,
∴(3﹣x)(6﹣x)=x2,
解得x=2,
∴AE=2,
过点E作EG⊥AB于点G,
在Rt△AEG中,∠EAG=60°,
∴AG=AE cos60°=2×=1,
EG=AE sin60°=2×=,
∴BG=AB﹣AG=6﹣1=5,
在Rt△BGE中,tan∠ABE==,
∴tan∠ACF=tan∠ABE=,
综上所述,当△PEC为直角三角形时,
tan∠ACF的值为或.
17.(1)证明:连接CM,PB,DM,如图1所示:
∵∠C=90°,四边形BCPM为圆内接四边形,
∴∠C+∠BMP=180°,
∴∠BMP=90°,BP为⊙O的直径,
又∵PD∥AB,
∴∠DPM=180°﹣∠BMP=90°,
∴MD为⊙O的直径,
∵∠C=90°,M为AB的中点,
∴CM=AB=BM,
∴,
又∵MD为⊙O的直径,
∴DM垂直平分BC,
∴PC∥MD,
∴四边形APDM为平行四边形;
(2)解:连接BD、CD、BP,如图2所示:
∵MD和BP均为⊙O的直径,
∴∠DPM=∠PMB=∠PDB=90°,
∴四边形PDBM为矩形,
∴PM=BD,
∵PM=PC,
∴PC=BD,
在Rt△BPD和Rt△PBC中,,
∴Rt△BPD≌Rt△PBC(HL),
∴PD=BC,
在Rt△ACB中,AC=4,tanA==,
∴BC=4tanA=2,
∴PD=BC=2.
18.(1)证明:∵AF⊥BC,
∴∠ADC=90°,
∴∠ACB+∠CAF=90°,
∵AE是⊙O的直径,
∴∠ABE=90°,
∴∠BAE+∠E=90°,
由圆周角定理得,∠ACB=∠E,
∴∠BAE=∠CAF;
(2)解:由圆周角定理得,∠ABG=∠AFC,又∠BAE=∠CAF,
∴△ABG∽△AFC,
∴=,即=,
解得,AF=.
19.解:(1)证明:∵CE⊥AD,
∴EG=CG,
∵CF∥DE,
∴∠DEG=∠FCG,
∵∠FGC=∠DGE,
∴△DEG≌△FCG(ASA),
∴ED=FC,
∴四边形DCFE为平行四边形,
又∵CE⊥DF,
∴四边形DCFE是菱形;
(2)∵AG⊥EC,EG=CG,
∴AE=AC=4,
∵四边形AEDC内接于⊙O,
∴∠BED=∠BCA=90°,
∵四边形DCFE是菱形,
∴EF∥DC,DE=DC,
∴∠AEF=∠ABC,
∴tan∠ABC=tan∠AEF=,
在Rt△BED中,设DE=3a,则BE=4a,
∴DC=3a,BD==5a,
∵BC2+AC2=AB2,
∴(5a+3a)2+42=(4a+4)2,
解得a=或a=0(舍去),
∴DE=DC=2,
∴AD===2.
即⊙O的直径长为2.
20.(1)证明:如图1,∵PC=PB,
∴∠PCB=∠PBC,
∵四边形ABCD内接于圆,
∴∠BAD+∠BCD=180°,
∵∠BCD+∠PCB=180°,
∴∠BAD=∠PCB,
∵∠BAD=∠BFD,
∴∠BFD=∠PCB=∠PBC,
∴BC∥DF,
∵DE⊥AB,
∴∠DEB=90°,
∴∠ABC=90°,
∴AC是⊙O的直径,
∴∠ADC=90°,
∵BG⊥AD,
∴∠AGB=90°,
∴∠ADC=∠AGB,
∴BG∥CD;
(2)由(1)得:BC∥DF,BG∥CD,
∴四边形BCDH是平行四边形,
∴BC=DH,
在Rt△ABC中,∵AB=DH,
∴tan∠ACB==,
∴∠ACB=60°,∠BAC=30°,
∴∠ADB=60°,BC=AC,
∴DH=AC,
①当点O在DE的左侧时,如图2,作直径DM,连接AM、OH,则∠DAM=90°,
∴∠AMD+∠ADM=90°
∵DE⊥AB,
∴∠BED=90°,
∴∠BDE+∠ABD=90°,
∵∠AMD=∠ABD,
∴∠ADM=∠BDE,
∵DH=AC,
∴DH=OD,
∴∠DOH=∠OHD=80°,
∴∠ODH=20°
∵∠ADB=60°,
∴∠ADM+∠BDE=40°,
∴∠BDE=∠ADM=20°,
②当点O在DE的右侧时,如图3,作直径DN,连接BN,
由①得:∠ADE=∠BDN=20°,∠ODH=20°,
∴∠BDE=∠BDN+∠ODH=40°,
综上所述,∠BDE的度数为20°或40°.
