2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.8圆内接正多边形 解答题专题提升训练(word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 524.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 19:16:43 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3-8圆内接正多边形》
解答题专题提升训练(附答案)
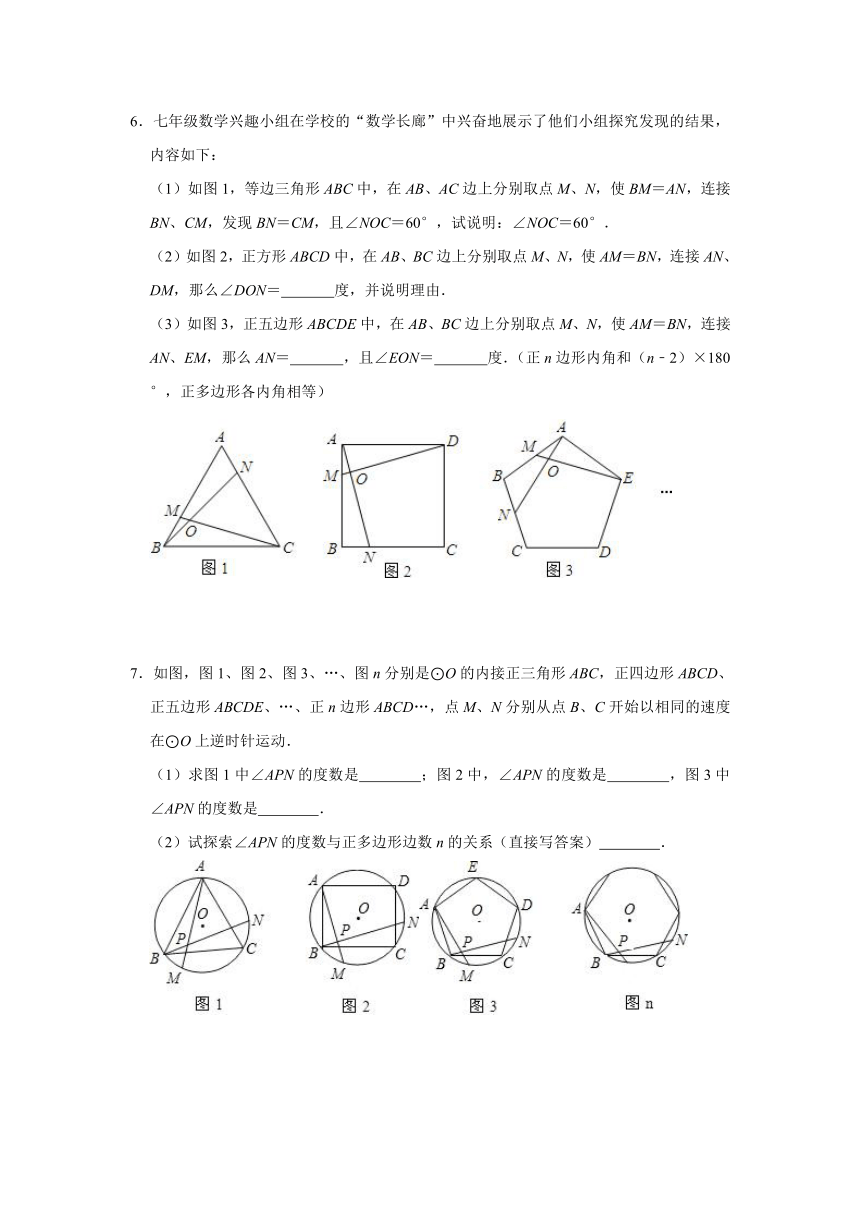
1.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
2.已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
3.如图,点M、N分别在正五边形ABCDE的边BC、CD上,且BM=CN,AM交BN于点P.
(1)求证:AM=BN;
(2)求∠APN的度数.
4.【阅读理解】
[阅读与思考]
如图①,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则AN=CM,∠NOC= ;
如图②,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,∠NOD= ;
如图③,在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,∠NOE= ;
[理解与运用]
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF= ;
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ= ;
[归纳与总结]
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即点M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于O.也会有类似的结论,你的结论是 .
5.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
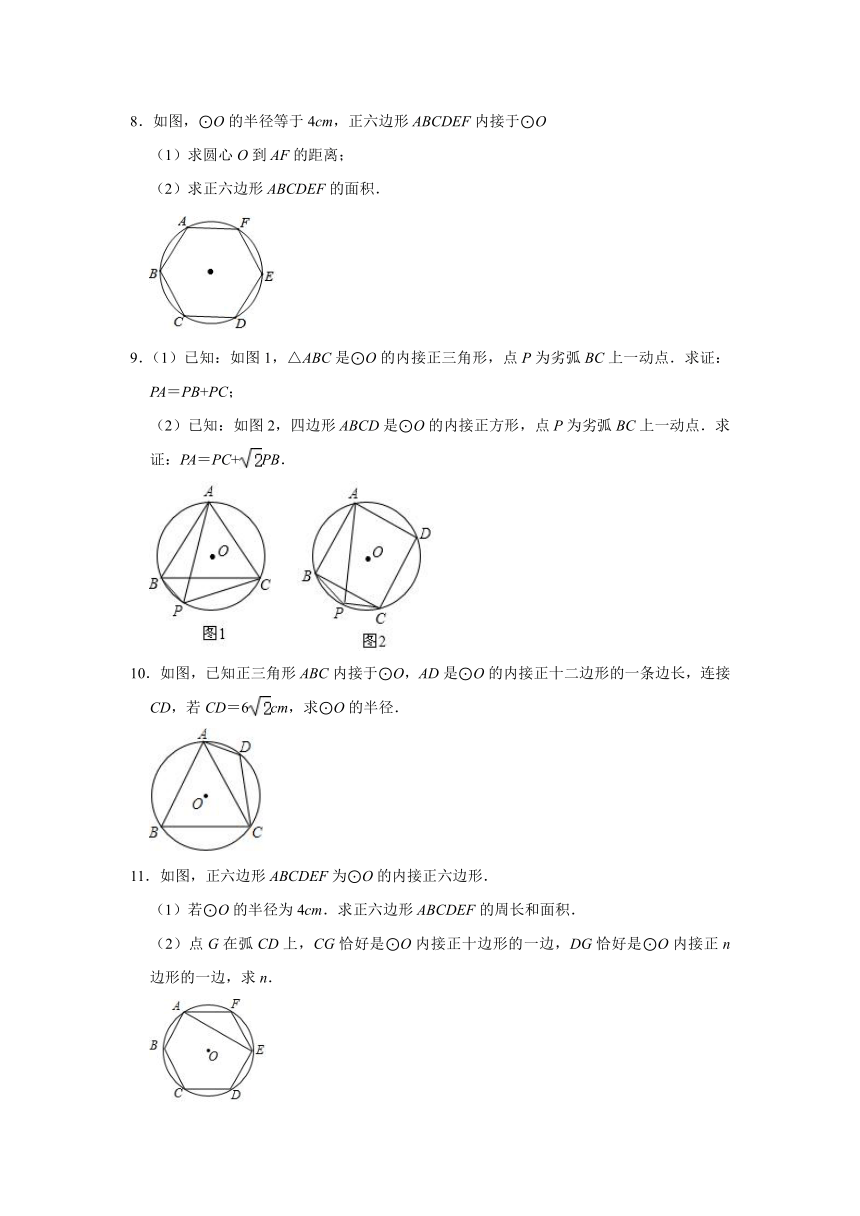
6.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°,试说明:∠NOC=60°.
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么∠DON= 度,并说明理由.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN= ,且∠EON= 度.(正n边形内角和(n﹣2)×180°,正多边形各内角相等)
7.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是 ;图2中,∠APN的度数是 ,图3中∠APN的度数是 .
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案) .
8.如图,⊙O的半径等于4cm,正六边形ABCDEF内接于⊙O
(1)求圆心O到AF的距离;
(2)求正六边形ABCDEF的面积.
9.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
10.如图,已知正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边长,连接CD,若CD=6cm,求⊙O的半径.
11.如图,正六边形ABCDEF为⊙O的内接正六边形.
(1)若⊙O的半径为4cm.求正六边形ABCDEF的周长和面积.
(2)点G在弧CD上,CG恰好是⊙O内接正十边形的一边,DG恰好是⊙O内接正n边形的一边,求n.
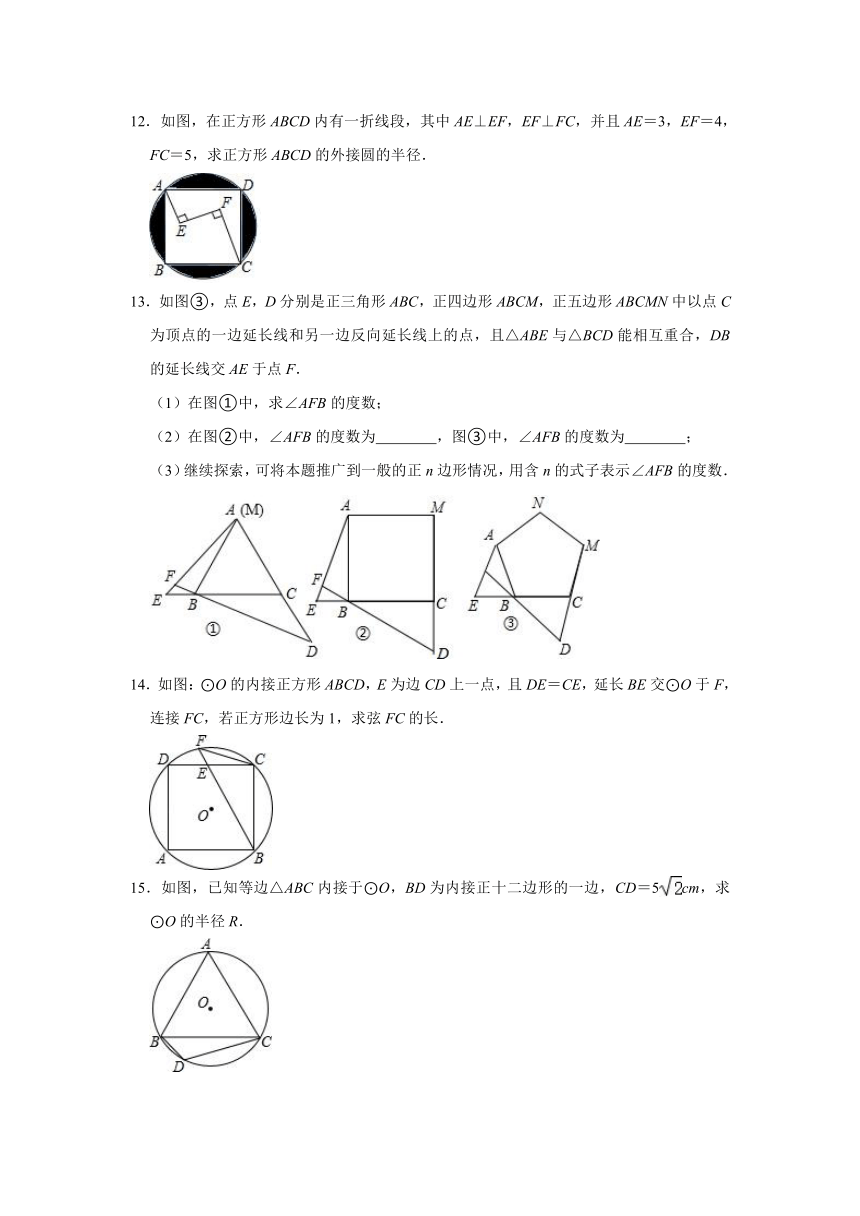
12.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
13.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数;
(2)在图②中,∠AFB的度数为 ,图③中,∠AFB的度数为 ;
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
14.如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连接FC,若正方形边长为1,求弦FC的长.
15.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
16.如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
17.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
18.已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:AB2=AG BF;
(2)证明:EG与⊙O相切,并求AG、BF的长.
19.如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O.若正△ABC的边长为6,求正方形DEFG的面积.
20.如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a.
(2)如图2,点O是AD的中点,联结OM、ON,求证:OM=ON.
参考答案
1.(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
2.(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=∠CDO+∠ODE=45°+22.5°=67.5°,
∴∠CED=180°﹣DCE﹣∠CDE=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,DE=DE,
∴Rt△PDE≌Rt△ODE(HL),
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
3.(1)证明:∵多边形ABCDE是正五边形,
∴AB=BC,∠ABM=∠BCN,
在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴AM=BN;
(2)解:∵多边形ABCDE是正五边形,
∴∠ABC=∠ABN+∠CBN=,
∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠APN是△ABP的外角,
∴∠APN=∠ABN+∠BAM=∠ABN+∠CBN=108°.
4.解:[阅读与思考]
∵在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,
∴∠B=∠CAM,AB=AC,
∵在△ABN和△CAM中
,
∴△ABN≌△CAM(SAS),
∴AN=CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA=∠OAC+∠BAN=∠BAC=60°,
故答案为:60°;
∵在正方形ABCD中,点M,N是AB,BC上的点,且AN=DM,
∴AD=AB,
在△ABN和△DAM中,
,
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠DAN+∠ADM=90°,
答案为:90°;
∵在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,
∴AB=AE,∠EAM=∠ABN,
∵在△AEM和△BAN中,
,
∴△ABN≌△EAM(SAS),
∴AN=EM,∠AEM=∠BAN,
∴∠EON=∠AEM+∠EAO=108°,
故答案为:108°;
[理解与运用]
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
所以同理可得:
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=120°;
故答案为:120°;
同理可得:
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=144°;
故答案为:144°;
[归纳与总结]
根据以上所求的角恰好等于正n边形的内角,
所以所求的角恰好等于正n边形的内角.
故答案为:以上所求的角恰好等于正n边形的内角.
5.(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∵∠ACB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
6.(1)证明:∵△ABC是正三角形,
∴∠A=∠ABC=60°,AB=BC,
在△ABN和△BCM中,,
∴△ABN≌△BCM(SAS),
∴∠ABN=∠BCM,
又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∴∠NOC=60°;
(2)解:∵四边形ABCD是正方形,
∴∠DAM=∠ABN=90°,AD=AB,
又∵AM=BN,
∴△ABN≌△DAM(SAS),
∴AN=DM,∠ADM=∠BAN,
又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°
∴∠AOM=90°;即∠DON=90°;
(3)解:∵五边形ABCDE是正五边形,
∴∠A=∠B,AB=AE,
又∵AM=BN,
∴△ABN≌△EAM(SAS),
∴AN=ME,
∴∠AEM=∠BAN,
∴∠NOE=∠NAE+∠AEM=∠NAE+∠BAN=∠BAE=108°.
故答案为:90°,EM,108°.
7.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
8.解:(1)过O作OH⊥AF于H,连接OA,OF,
∵在正六边形ABCDEF中,∠BAF=120°,
∴∠OAF=60°,
∵OA=4,
∴AH=OA=2,
∴OH===2;
∴圆心O到AF的距离为2;
(2)∵OA=OF,∠OAF=60°,
∴△OAF是等边三角形,
∴AF=OA=4,
∴S△AOF=×4×2=4,
∴正六边形ABCDEF的面积=6S△AOF=24.
9.证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=∠AOB=45°,
∴BP=BE,
∴PE=PB,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+PB;
10.解:连接OA、OD、OC,如图所示:
∵等边△ABC内接于⊙O,AD为内接正十二边形的一边,
∴∠AOC=×360°=120°,∠AOD=×360°=30°,
∴∠COD=∠AOC﹣∠BAD=90°,
∵OC=OD,
∴△OCD是等腰直角三角形,
∴OC=OD=CD=×6=6,
即⊙O的半径为6cm.
11.解:(1)连接OC,OD,
∵六边形ABCDEF是圆内接正六边形,
∴∠AOD==60°,
∵OC=OD,
∴△COD是正三角形,
∴CD=OC=OD=4(cm),
∴正六边形ABCDEF的周长为4×6=24(cm),
∵S△COD=×4××4=4(cm2),
∴S正六边形ABCDEF=6S△COD=24(cm2),
答:正六边形ABCDEF的周长为24cm,面积为24cm2;
(2)连接OG,
∵CG是正十边形的边长,
∴∠COG==36°,
∴∠DOG=∠COD﹣∠COG=60°﹣36°=24°,
∵DG是圆内接正n边形的边长,
∴=24°,
解得n=15.
12.解:连接AC,则AC是该圆的直径,延长AE交圆于G,
连接CG,则∠AGC=90°,
∵AE⊥EF,EF⊥FC,
∵四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得,AC==4,
∴正方形外接圆的半径为2.
13.解:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∴∠ABE=∠BCD=120°.
∵△ABE与△BCD能相互重合,
∴∠E=∠D,∠DBC=∠BAE.
∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°;
(2)图②中,∵△ABE与△BCD能相互重合,
∴∠E=∠D.
∵∠FBE=∠CBD,∠D+∠CBD=90°,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=90°;
同理可得,图③中∠AFB=108°.
故答案为:90°,108°;
(3)由(1)(2)可知,在正n边形中,∠AFB=.
14.解:连接BD.
∵CE=×1=,
∴BE==,
在Rt△ABD中,BD==,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴=,
∴=,
∴FC=.
15.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD cos45°=5×=5(cm).
即⊙O的半径R=5cm.
16.(1)解:∵DC=BC,
∴△CDB是等腰三角形,
∵∠C=108°,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
进而可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°﹣36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
故∠G=180°﹣∠2﹣∠F=180°﹣72°﹣36°=72°=2∠F.
17.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.(2分)
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.(4分)
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴(7分)
18.证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴,即BC AE=AG BF.
又∵BC=AE=AB,
∴AB2=AG BF.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,
∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴EG2=AG BG.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则22=x(x+2),解得x=,
∴AG=,代入①中可得:BF=.
19.解:设⊙O与BC相切于点M,连接OM、OB、OD、OE,如图所示:
则∠OMB=90°,∠OBM=30°,
∴BM=BC==3,
∴OM=BM tan30°=3×=,
∴OD=OE=,
∵四边形DEFG是正方形,
∴∠DOE=90°,
∴△DOE是等腰直角三角形,
∴DE=OD==,
即正方形的DEFG的面积为6.
20.解:(1)①∵六边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN,
∵正六边形ABCDEF中,PM∥AB,PN∥CD,
∴∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM=AM,HP=BP,PL=PC,NK=ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)如图2,连接OE,
∵六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△ONE和△OMA中,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
解答题专题提升训练(附答案)
1.如图,正方形ABCD内接于⊙O,E是的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
2.已知,正方形ABCD内接于⊙O,点P是弧AD上一点.
(1)如图1,若点P是弧AD的中点,求证:CE=CD;
(2)如图2,若图中PE=OE,求的值.
3.如图,点M、N分别在正五边形ABCDE的边BC、CD上,且BM=CN,AM交BN于点P.
(1)求证:AM=BN;
(2)求∠APN的度数.
4.【阅读理解】
[阅读与思考]
如图①,在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,则AN=CM,∠NOC= ;
如图②,在正方形ABCD中,点M,N是AB,BC上的点,且AM=BN,则AN=DM,∠NOD= ;
如图③,在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,∠NOE= ;
[理解与运用]
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF= ;
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ= ;
[归纳与总结]
根据以上规律,在正n边形A1A2A3A4…An中,对相邻的三边实施同样的操作过程,即点M,N是A1A2,A2A3上的点,且A1M=A2N,A1N与AnM相交于O.也会有类似的结论,你的结论是 .
5.如图,A,P,B,C是⊙O上的四个点,∠APC=∠CPB=60°.
(1)求证:△ABC是等边三角形.
(2)若⊙O的半径为2,求等边△ABC的边心距.
6.七年级数学兴趣小组在学校的“数学长廊”中兴奋地展示了他们小组探究发现的结果,内容如下:
(1)如图1,等边三角形ABC中,在AB、AC边上分别取点M、N,使BM=AN,连接BN、CM,发现BN=CM,且∠NOC=60°,试说明:∠NOC=60°.
(2)如图2,正方形ABCD中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、DM,那么∠DON= 度,并说明理由.
(3)如图3,正五边形ABCDE中,在AB、BC边上分别取点M、N,使AM=BN,连接AN、EM,那么AN= ,且∠EON= 度.(正n边形内角和(n﹣2)×180°,正多边形各内角相等)
7.如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动.
(1)求图1中∠APN的度数是 ;图2中,∠APN的度数是 ,图3中∠APN的度数是 .
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案) .
8.如图,⊙O的半径等于4cm,正六边形ABCDEF内接于⊙O
(1)求圆心O到AF的距离;
(2)求正六边形ABCDEF的面积.
9.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为劣弧BC上一动点.求证:PA=PB+PC;
(2)已知:如图2,四边形ABCD是⊙O的内接正方形,点P为劣弧BC上一动点.求证:PA=PC+PB.
10.如图,已知正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边长,连接CD,若CD=6cm,求⊙O的半径.
11.如图,正六边形ABCDEF为⊙O的内接正六边形.
(1)若⊙O的半径为4cm.求正六边形ABCDEF的周长和面积.
(2)点G在弧CD上,CG恰好是⊙O内接正十边形的一边,DG恰好是⊙O内接正n边形的一边,求n.
12.如图,在正方形ABCD内有一折线段,其中AE⊥EF,EF⊥FC,并且AE=3,EF=4,FC=5,求正方形ABCD的外接圆的半径.
13.如图③,点E,D分别是正三角形ABC,正四边形ABCM,正五边形ABCMN中以点C为顶点的一边延长线和另一边反向延长线上的点,且△ABE与△BCD能相互重合,DB的延长线交AE于点F.
(1)在图①中,求∠AFB的度数;
(2)在图②中,∠AFB的度数为 ,图③中,∠AFB的度数为 ;
(3)继续探索,可将本题推广到一般的正n边形情况,用含n的式子表示∠AFB的度数.
14.如图:⊙O的内接正方形ABCD,E为边CD上一点,且DE=CE,延长BE交⊙O于F,连接FC,若正方形边长为1,求弦FC的长.
15.如图,已知等边△ABC内接于⊙O,BD为内接正十二边形的一边,CD=5cm,求⊙O的半径R.
16.如图,已知正五边形ABCDE,AF∥CD交DB的延长线于点F,交DE的延长线于点G.
(1)写出图中所有的等腰三角形;
(2)求证:∠G=2∠F.
17.(1)已知:如图1,△ABC是⊙O的内接正三角形,点P为弧BC上一动点,求证:PA=PB+PC;
(2)如图2,四边形ABCD是⊙O的内接正方形,点P为弧BC上一动点,求证:;
(3)如图3,六边形ABCDEF是⊙O的内接正六边形,点P为弧BC上一动点,请探究PA、PB、PC三者之间有何数量关系,并给予证明.
18.已知:如图,边长为2的正五边形ABCDE内接于⊙O,AB、DC的延长线交于点F,过点E作EG∥CB交BA的延长线于点G.
(1)求证:AB2=AG BF;
(2)证明:EG与⊙O相切,并求AG、BF的长.
19.如图,正△ABC外切于⊙O,正方形DEFG内接于⊙O.若正△ABC的边长为6,求正方形DEFG的面积.
20.如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a.
(2)如图2,点O是AD的中点,联结OM、ON,求证:OM=ON.
参考答案
1.(1)证明:∵四边形ABCD是正方形,
∴AB=CD,
∴=,
∵E是的中点,
∴=,
∴+=+,即=,
∴AE=DE.
(2)解:连接BD,AO,过点D作DF⊥DE交EC的延长线于F.
∵四边形ABCD是正方形,
∴∠DBC=∠DEC=45°,DA=DC,
∵∠EDF=90°,
∴∠F=∠EDF﹣∠DEF=90°﹣45°=45°,
∴DE=DF,
∵∠AED=∠AOD=45°,
∴∠AED=∠F=45°,
∵∠ADC=∠EDF=90°,
∴∠ADE+∠EDC=∠CDF+∠EDC=90°,
∴∠ADE=∠CDF
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS),
∴AE=CF,
∴S△ADE=S△CDF,
∴S四边形AECD=S△DEF,
∵EF=DE=EC+DE,EC=1,
∴1+DE=DE,
∴DE=+1,
∴S四边形AECD=S△DEF=DE2=+.
2.(1)证明:如图1,连接DE,
∵四边形ABCD是正方形,
∴AC⊥BD,OB=OD=OC,
∴EB=ED,∠ODC=∠OCD=45°,
∴∠EBD=∠EDB,
∵点P是弧AD的中点,
∴∠PBD=∠ABD=×∠AOD=22.5°,
∴∠EDC=∠CDO+∠ODE=45°+22.5°=67.5°,
∴∠CED=180°﹣DCE﹣∠CDE=180°﹣45°﹣67.5°=67.5°,
∴∠CED=∠EDC,
∴CE=CD;
(2)解:如图2,连接DE,DP,
∵四边形ABCD是正方形,
∴∠BAD=∠EOD=90°,OA=OD,
∴∠P=∠BAD=90°,
∵PE=OE,DE=DE,
∴Rt△PDE≌Rt△ODE(HL),
∴∠PDE=∠2,由(1)知∠1=∠2,
∴∠1=∠2=∠PDE,
∴∠1+∠2+∠PDE=90°,
∴∠2=30°,
∴OE=DE,
∴DE=2OE,
∴OD==OE,
∴=,
∴OD=OA=OE,
∴AE=OA﹣OE=(﹣1)OE,EC=OE+OC=(+1)OE,
∴==2﹣.
3.(1)证明:∵多边形ABCDE是正五边形,
∴AB=BC,∠ABM=∠BCN,
在△ABM和△BCN中,
,
∴△ABM≌△BCN(SAS),
∴AM=BN;
(2)解:∵多边形ABCDE是正五边形,
∴∠ABC=∠ABN+∠CBN=,
∵△ABM≌△BCN,
∴∠BAM=∠CBN,
∵∠APN是△ABP的外角,
∴∠APN=∠ABN+∠BAM=∠ABN+∠CBN=108°.
4.解:[阅读与思考]
∵在正三角形ABC中,点M,N是AB,BC上的点,且AM=BN,
∴∠B=∠CAM,AB=AC,
∵在△ABN和△CAM中
,
∴△ABN≌△CAM(SAS),
∴AN=CM,∠BAN=∠MCA,
∴∠NOC=∠OAC+∠MCA=∠OAC+∠BAN=∠BAC=60°,
故答案为:60°;
∵在正方形ABCD中,点M,N是AB,BC上的点,且AN=DM,
∴AD=AB,
在△ABN和△DAM中,
,
∴△ABN≌△DAM(SAS),
∴∠AMD=∠ANB,∠ADM=∠BAN,
∴∠DON=∠DAN+∠ADM=90°,
答案为:90°;
∵在正五边形ABCDE中,点M,N是AB,BC上的点,且AM=BN,则AN=EM,
∴AB=AE,∠EAM=∠ABN,
∵在△AEM和△BAN中,
,
∴△ABN≌△EAM(SAS),
∴AN=EM,∠AEM=∠BAN,
∴∠EON=∠AEM+∠EAO=108°,
故答案为:108°;
[理解与运用]
∵正三角形的内角度数为:60°,
正方形的内角度数为:90°,
正五边形的内角度数为:108°,
所以同理可得:
在正六边形ABCDEF中,点M,N是AB,BC上的点,且AM=BN,则AN=FM,∠NOF=120°;
故答案为:120°;
同理可得:
在正十边形ABCDEFGHIJ中,点M,N是AB,BC上的点,且AM=BN,则AN=JM,∠NOJ=144°;
故答案为:144°;
[归纳与总结]
根据以上所求的角恰好等于正n边形的内角,
所以所求的角恰好等于正n边形的内角.
故答案为:以上所求的角恰好等于正n边形的内角.
5.(1)证明:在⊙O中,
∵∠BAC与∠CPB是对的圆周角,∠ABC与∠APC是所对的圆周角,
∴∠BAC=∠CPB,∠ABC=∠APC,
又∵∠APC=∠CPB=60°,
∴∠ABC=∠BAC=60°,
∵∠ACB=60°,
∴∠ABC=∠BAC=∠ACB=60°,
∴△ABC为等边三角形;
(2)过O作OD⊥BC于D,连接OB,
则∠OBD=30°,∠ODB=90°,
∵OB=2,
∴OD=1,
∴等边△ABC的边心距为1.
6.(1)证明:∵△ABC是正三角形,
∴∠A=∠ABC=60°,AB=BC,
在△ABN和△BCM中,,
∴△ABN≌△BCM(SAS),
∴∠ABN=∠BCM,
又∵∠ABN+∠OBC=60°,
∴∠BCM+∠OBC=60°,
∴∠NOC=60°;
(2)解:∵四边形ABCD是正方形,
∴∠DAM=∠ABN=90°,AD=AB,
又∵AM=BN,
∴△ABN≌△DAM(SAS),
∴AN=DM,∠ADM=∠BAN,
又∵∠ADM+∠AMD=90°,
∴∠BAN+∠AMD=90°
∴∠AOM=90°;即∠DON=90°;
(3)解:∵五边形ABCDE是正五边形,
∴∠A=∠B,AB=AE,
又∵AM=BN,
∴△ABN≌△EAM(SAS),
∴AN=ME,
∴∠AEM=∠BAN,
∴∠NOE=∠NAE+∠AEM=∠NAE+∠BAN=∠BAE=108°.
故答案为:90°,EM,108°.
7.解:(1)图1:∵点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动,
∴∠BAM=∠CBN,
又∵∠APN=∠BPM,
∴∠APN=∠BPM=∠ABN+∠BAM=∠ABN+∠CBN=∠ABC=60°;
同理可得:在图2中,∠APN=90°;在图3中,∠APN=108°.
(2)由(1)可知,∠APN=所在多边形的内角度数,故在图n中,.
8.解:(1)过O作OH⊥AF于H,连接OA,OF,
∵在正六边形ABCDEF中,∠BAF=120°,
∴∠OAF=60°,
∵OA=4,
∴AH=OA=2,
∴OH===2;
∴圆心O到AF的距离为2;
(2)∵OA=OF,∠OAF=60°,
∴△OAF是等边三角形,
∴AF=OA=4,
∴S△AOF=×4×2=4,
∴正六边形ABCDEF的面积=6S△AOF=24.
9.证明:(1)延长BP至E,使PE=PC,连接CE,如图1,
∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,
∵PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
在△BEC和△APC中,
,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC;
(2)过点B作BE⊥PB交PA于E,连接OA,OB.如图2,
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∵∠APB=∠AOB=45°,
∴BP=BE,
∴PE=PB,
在△ABE和△CBP中,
,
∴△ABE≌△CBP(SAS),
∴PC=AE,
∴PA=AE+PE=PC+PB;
10.解:连接OA、OD、OC,如图所示:
∵等边△ABC内接于⊙O,AD为内接正十二边形的一边,
∴∠AOC=×360°=120°,∠AOD=×360°=30°,
∴∠COD=∠AOC﹣∠BAD=90°,
∵OC=OD,
∴△OCD是等腰直角三角形,
∴OC=OD=CD=×6=6,
即⊙O的半径为6cm.
11.解:(1)连接OC,OD,
∵六边形ABCDEF是圆内接正六边形,
∴∠AOD==60°,
∵OC=OD,
∴△COD是正三角形,
∴CD=OC=OD=4(cm),
∴正六边形ABCDEF的周长为4×6=24(cm),
∵S△COD=×4××4=4(cm2),
∴S正六边形ABCDEF=6S△COD=24(cm2),
答:正六边形ABCDEF的周长为24cm,面积为24cm2;
(2)连接OG,
∵CG是正十边形的边长,
∴∠COG==36°,
∴∠DOG=∠COD﹣∠COG=60°﹣36°=24°,
∵DG是圆内接正n边形的边长,
∴=24°,
解得n=15.
12.解:连接AC,则AC是该圆的直径,延长AE交圆于G,
连接CG,则∠AGC=90°,
∵AE⊥EF,EF⊥FC,
∵四边形EFCG是矩形,
∴EG=FC=5,GC=EF=4,
∴AG=8.
由勾股定理得,AC==4,
∴正方形外接圆的半径为2.
13.解:(1)∵△ABC是等边三角形,
∴AB=BC,∠ABC=∠ACB=60°,
∴∠ABE=∠BCD=120°.
∵△ABE与△BCD能相互重合,
∴∠E=∠D,∠DBC=∠BAE.
∵∠FBE=∠CBD,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=∠ACB=60°;
(2)图②中,∵△ABE与△BCD能相互重合,
∴∠E=∠D.
∵∠FBE=∠CBD,∠D+∠CBD=90°,
∴∠AFB=∠E+∠FBE=∠D+∠CBD=90°;
同理可得,图③中∠AFB=108°.
故答案为:90°,108°;
(3)由(1)(2)可知,在正n边形中,∠AFB=.
14.解:连接BD.
∵CE=×1=,
∴BE==,
在Rt△ABD中,BD==,
∵∠DBE=∠FCE,∠CFE=∠BDE,
∴△DEB∽△FEC,
∴=,
∴=,
∴FC=.
15.解:连接OB,OC,OD,
∵等边△ABC内接于⊙O,BD为内接正十二边形的一边,
∴∠BOC=×360°=120°,∠BOD=×360°=30°,
∴∠COD=∠BOC﹣∠BOD=90°,
∵OC=OD,
∴∠OCD=45°,
∴OC=CD cos45°=5×=5(cm).
即⊙O的半径R=5cm.
16.(1)解:∵DC=BC,
∴△CDB是等腰三角形,
∵∠C=108°,
∴∠1=∠CBD=36°,
∵AF∥CD,
∴∠F=∠1=36°,
可得四边形DEAB是等腰梯形,
∴∠DBA=∠2=72°,
∴∠F=∠BAF=36°,
∴△BAF是等腰三角形,
进而可得:∠GEA=∠G=∠2=72°,
∴△FDG,△AEG是等腰三角形,
故等腰三角形有:△BCD,△ABF,△FDG,△AEG.
(2)证明:∵五边形ABCDE是正五边形,
∴∠C=∠CDE=108°,CD=CB.
得∠1=36°,
∴∠2=108°﹣36°=72°.
又∵AF∥CD,
∴∠F=∠1=36°,
故∠G=180°﹣∠2﹣∠F=180°﹣72°﹣36°=72°=2∠F.
17.证明:(1)延长BP至E,使PE=PC,
连接CE.∵A、B、P、C四点共圆,
∴∠BAC+∠BPC=180°,
∵∠BPC+∠EPC=180°,
∴∠BAC=∠CPE=60°,PE=PC,
∴△PCE是等边三角形,
∴CE=PC,∠E=60°;
又∵∠BCE=60°+∠BCP,∠ACP=60°+∠BCP,
∴∠BCE=∠ACP,
∵△ABC、△ECP为等边三角形,
∴CE=PC,AC=BC,
∴△BEC≌△APC(SAS),
∴PA=BE=PB+PC.(2分)
(2)过点B作BE⊥PB交PA于E.
∵∠1+∠2=∠2+∠3=90°
∴∠1=∠3,
∴∠APB=45°,
∴BP=BE,∴;
又∵AB=BC,
∴△ABE≌△CBP,
∴PC=AE.
∴.(4分)
(3)答:;
证明:过点B,作BM⊥AP,在AP上截取AQ=PC,
连接BQ,∵∠BAP=∠BCP,AB=BC,
∴△ABQ≌△CBP,
∴BQ=BP.
∴MP=QM,
又∵∠APB=30°,
∴cos30°=,
∴PM=PB,
∴
∴(7分)
18.证明:(1)易证五边形ABCDE的外角∠FCB=∠EAG=∠FBC,
∵EG∥CB,
∴∠EAG=∠FBC.
∴△EAG∽△FBC.
∴,即BC AE=AG BF.
又∵BC=AE=AB,
∴AB2=AG BF.①
(2)连接EF,由(1)可知FB=FC,即△FBC为等腰三角形,易知BA=CD,
∴FA=FD,
∴EF⊥BC且EF平分BC,
∴EF过圆心O.
又∵EG∥CB,∴EF⊥EG,
∴EG与⊙O相切.
∴EG2=AG BG.
由(1)可知∠G=∠EAG,∴EG=EA=2,
设AG=x,则22=x(x+2),解得x=,
∴AG=,代入①中可得:BF=.
19.解:设⊙O与BC相切于点M,连接OM、OB、OD、OE,如图所示:
则∠OMB=90°,∠OBM=30°,
∴BM=BC==3,
∴OM=BM tan30°=3×=,
∴OD=OE=,
∵四边形DEFG是正方形,
∴∠DOE=90°,
∴△DOE是等腰直角三角形,
∴DE=OD==,
即正方形的DEFG的面积为6.
20.解:(1)①∵六边形ABCDEF是正六边形,
∴∠A=∠B=∠C=∠D=∠E=∠F=120°
又∴PM∥AB,PN∥CD,
∴∠BPM=60°,∠NPC=60°,
∴∠MPN=180°﹣∠BPM﹣∠NPC=180°﹣60°﹣60°=60°,
故答案为:60°.
②如图1,作AG⊥MP交MP于点G,BH⊥MP于点H,CL⊥PN于点L,DK⊥PN于点K,
MP+PN=MG+GH+HP+PL+LK+KN,
∵正六边形ABCDEF中,PM∥AB,PN∥CD,
∴∠AMG=∠BPH=∠CPL=∠DNK=60°,
∴GM=AM,HP=BP,PL=PC,NK=ND,
∵AM=BP,PC=DN,
∴MG+HP+PL+KN=a,GH=LK=a,
∴MP+PN=MG+GH+HP+PL+LK+KN=3a.
(2)如图2,连接OE,
∵六边形ABCDEF是正六边形,AB∥MP,PN∥DC,
∴AM=BP=EN,
∵∠MAO=∠OEN=60°,OA=OE,
在△ONE和△OMA中,
,
∴△OMA≌△ONE(SAS),
∴OM=ON.
