2021-2022学年北师大版九年级数学下册3.7切线长定理 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.7切线长定理 解答题专题提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 416.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 19:21:55 | ||
图片预览

文档简介
2021-2022学年北师大版九年级数学下册《3-7切线长定理》解答题专题提升训练(附答案)
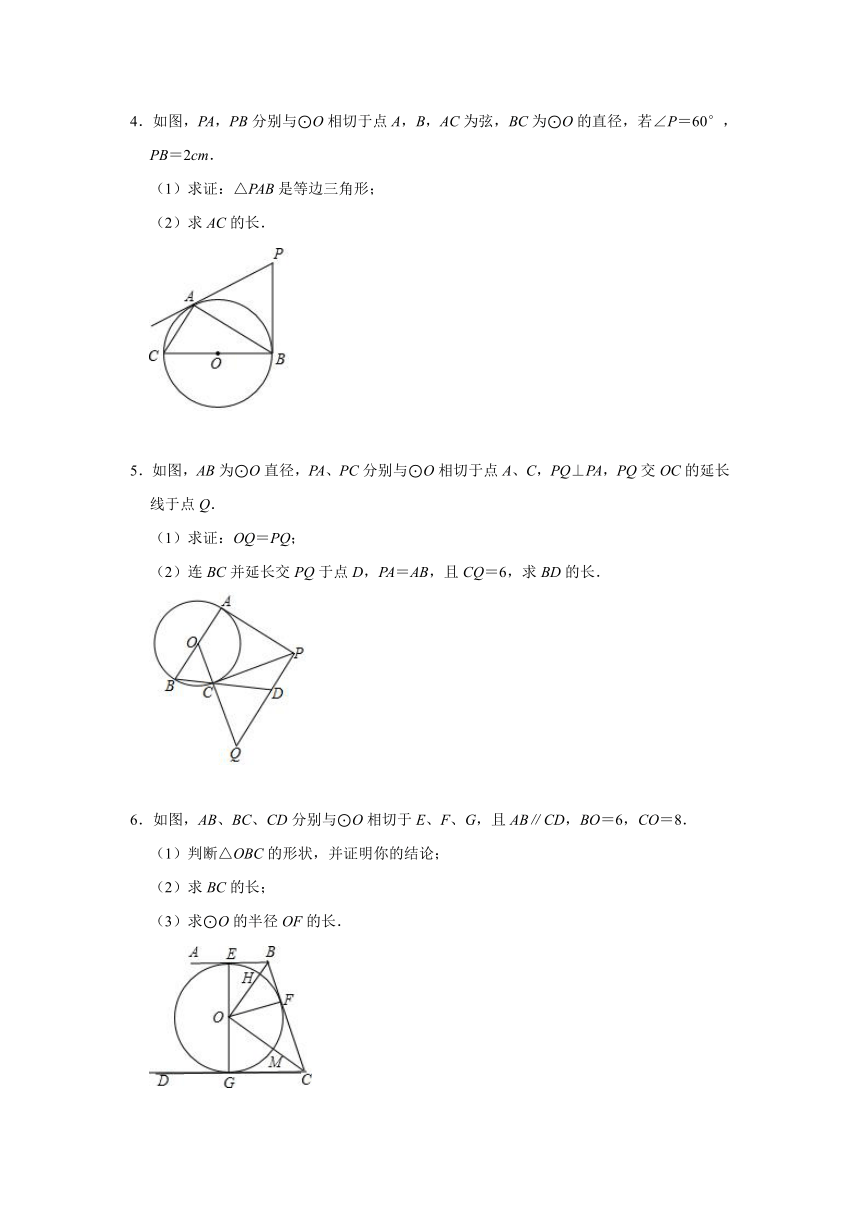
1.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
2.已知:AB为⊙O的直径,∠BAD=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.
①求BC的长;
②延长AE交BC的延长线于G点,求EG的长.
3.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
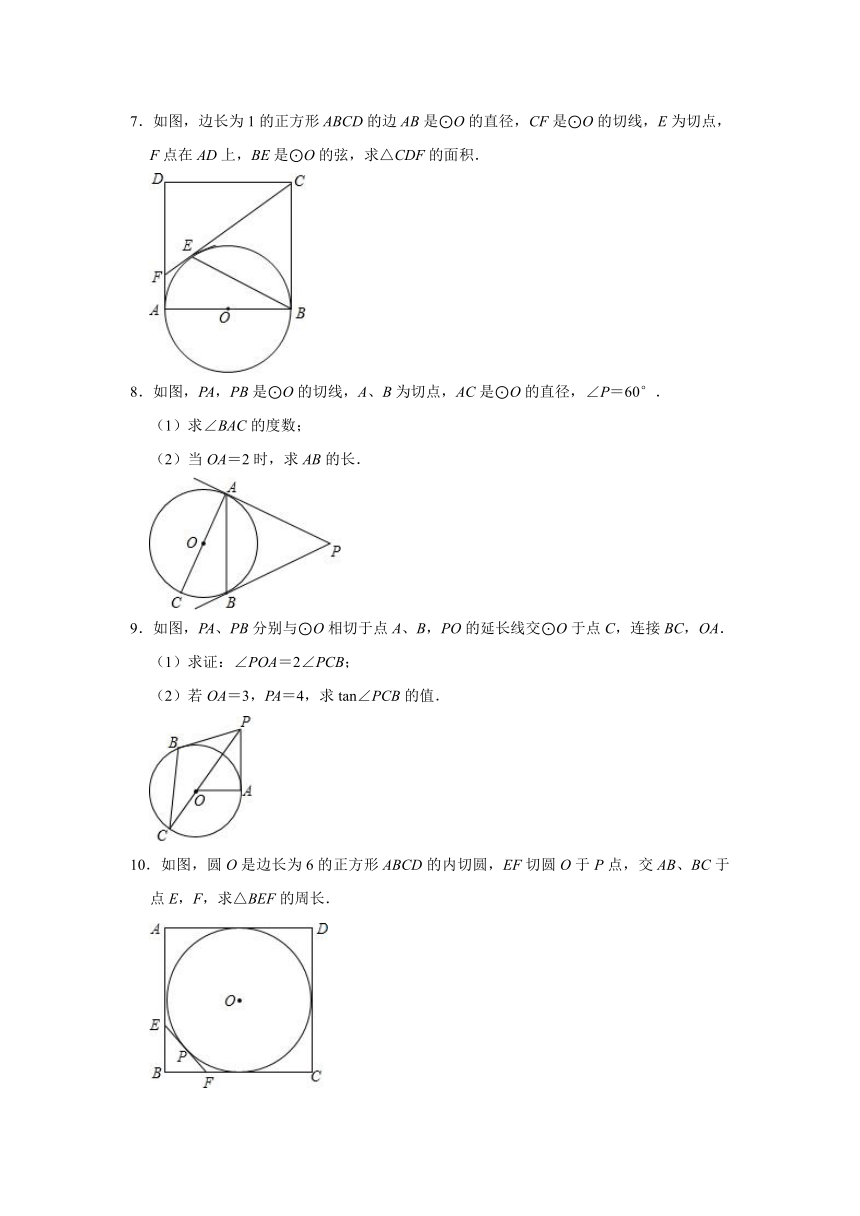
4.如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
5.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
6.如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求⊙O的半径OF的长.
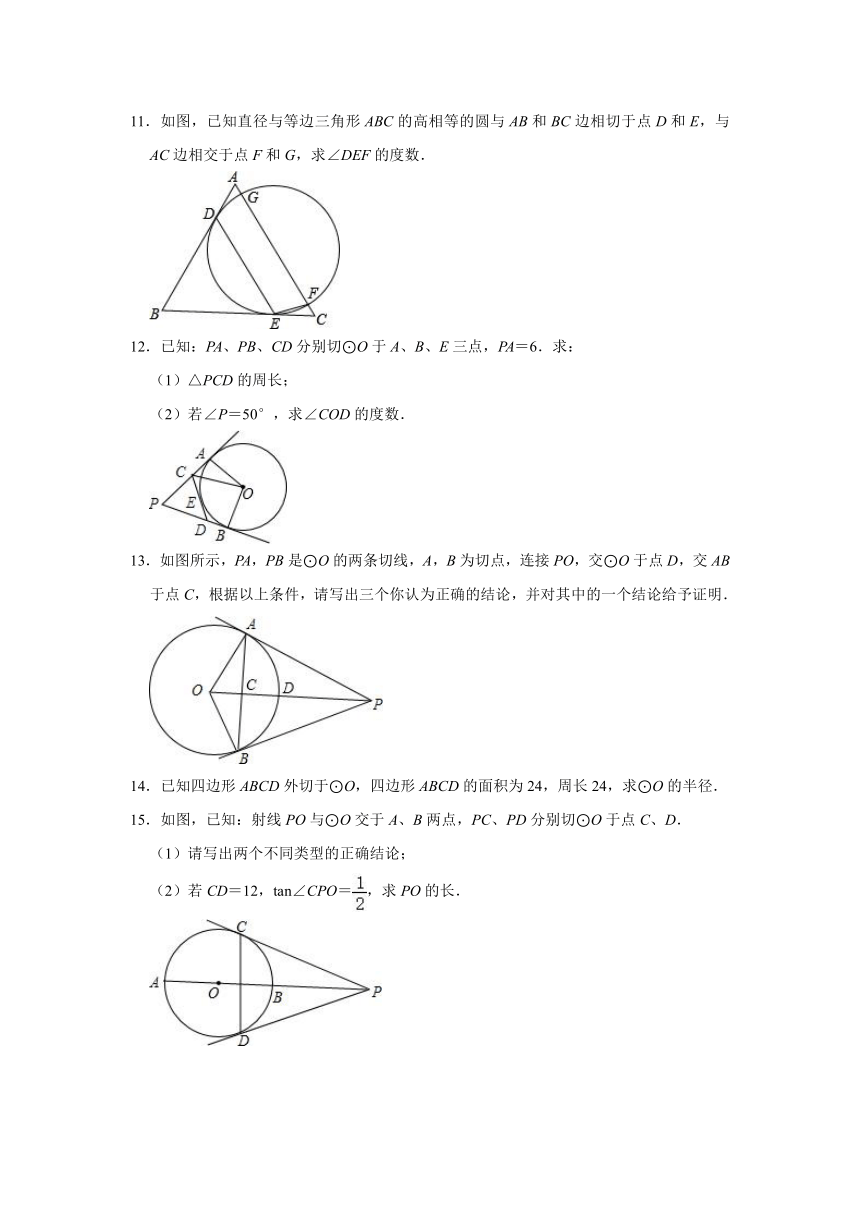
7.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
8.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
9.如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
(1)求证:∠POA=2∠PCB;
(2)若OA=3,PA=4,求tan∠PCB的值.
10.如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
11.如图,已知直径与等边三角形ABC的高相等的圆与AB和BC边相切于点D和E,与AC边相交于点F和G,求∠DEF的度数.
12.已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
13.如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
14.已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.
15.如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
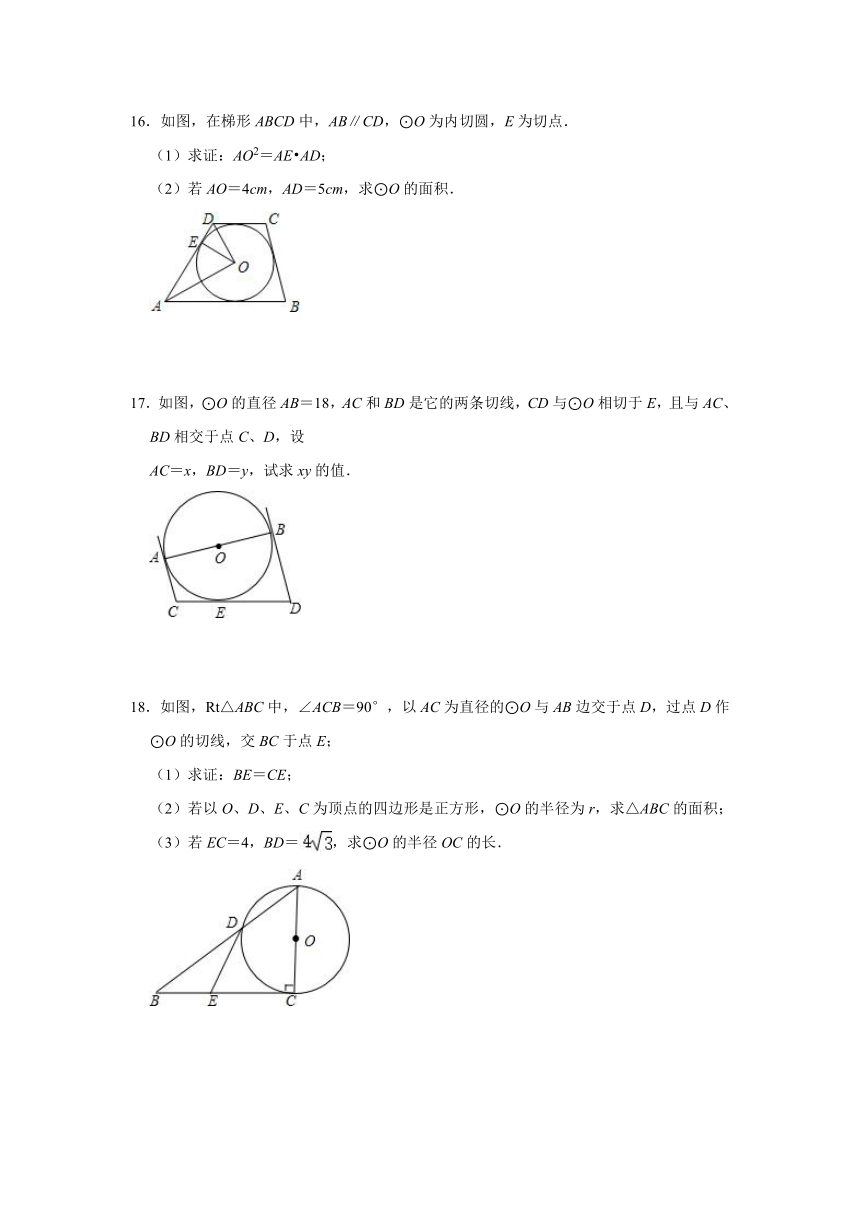
16.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(1)求证:AO2=AE AD;
(2)若AO=4cm,AD=5cm,求⊙O的面积.
17.如图,⊙O的直径AB=18,AC和BD是它的两条切线,CD与⊙O相切于E,且与AC、BD相交于点C、D,设
AC=x,BD=y,试求xy的值.
18.如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E;
(1)求证:BE=CE;
(2)若以O、D、E、C为顶点的四边形是正方形,⊙O的半径为r,求△ABC的面积;
(3)若EC=4,BD=,求⊙O的半径OC的长.
19.已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DF DC?若存在,作出点F,并予以证明;若不存在,请说明理由.
20.如图1,PA,PB是⊙O的切线,A,B为切点,C为上的一点,∠COA=∠P.
(1)求证:BC∥OA;
(2)如图2,若BC=10,OA=13,求PA的长.
参考答案
1.解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
2.解:①过点D作DF⊥BC于点F,
∵AB为⊙O的直径,∠BAD=∠B=90°,
∴四边形ABFD是矩形,AD与BC是⊙O的切线,
∴DF=AB=2,BF=AD=2,
∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,
则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,
在Rt△DCF中,DC2=CF2+DF2,
即(2+x)2=(x﹣2)2+(2)2,
解得:x=,
即BC=;
②∵AB为⊙O的直径,∠BAD=∠B=90°,
∴AD∥BC,
∴△ADE∽△GCE,
∴AD:CG=DE:CE,AE:EG=AD:CG,
∵AD=DE=2,
∴CG=CE=BC=,
∴BG=BC+CG=5,
∴AE:EG=4:5,
在Rt△ABG中,AG==3,
∴EG=AG=.
3.解:(1)∵DA,DC都是圆O的切线,
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,
∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=(180﹣40)=70°,
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°﹣70°=20°
∴∠AFB=90°﹣20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
4.解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=cm.
5.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
6.(1)答:△OBC是直角三角形.
证明:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形;
(2)解:∵在Rt△BOC中,BO=6,CO=8,
∴BC==10;
(3)解:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴OF⊥BC,
∴OF===4.8.
7.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
8.解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
9.证明:(1)连接OB,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB,∠OBP=∠OAP=90°,
在Rt△POA和Rt△POB中,
∵,
∴Rt△POA≌Rt△POB(HL),
∴∠POA=∠POB,
∵∠POB=2∠PCB,
∴∠POA=2∠PCB;
(2)过B作BE⊥PC于E,
∵PB=PA=4,OB=OA=3,
∴PO=5,
∴PO BE=OB PB,
∴BE=,
由勾股定理得:OE==,
∴CE=OC+OE=3+=,
在Rt△OBE中,tan∠PCB===.
10.解:设⊙O切AB于M,切BC于N,连接OM、ON,
则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ON=AB=×6=3,
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
11.解:过点E作BC的垂线与圆交于点H,与AC交于点O.
连接AH和DH,作AM⊥BC,垂足为M.
∵E为切点,∴EH必过圆心,即EH是直径,
∴DH⊥DE,
∵D、E是切点,∴BD=BE,
∵∠B=60°,∴△DBE是正三角形,
∴∠BDE=∠BAC=60°,
∴DE∥AC,DH⊥AC,
由已知得,AM=EH,又AM∥EH,∴四边形AMEH是矩形,
∴AH⊥HE,即AH是切线,
∴AD=AH,AC垂直平分DH,AC必过圆心,
∴AC与EH的交点O是圆心,
∴OE=OF,
∵∠COE=90°﹣∠C=30°,∴∠OEF=75°,
∵∠DEO=∠EOC=30°,
∴∠DEF=30°+75°=105°
法二:过点E作BC的垂线与圆交于点H,与AC交于点O.
∵BC为切线
∴O为圆心,OE⊥BC.
∵OE=OF
∴∠OFE=∠OEF.
∴∠OEF=∠C+∠FEC,∠FEC=∠OEF﹣∠C
又∵∠OEC=90°,
∴∠OEF+∠FEC=90°
即2∠OEF﹣∠C=90°.
∵∠C=60°,
∴∠OEF=75°,∠CEF=15°.
又∵AC∥DE,∠C=60°,
∴∠DEC=120°.
∵∠CEF=15°,
∴∠DEF=105°
12.解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=BD,CE=AC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB=×130°=65°.
13.解:如图所示,结论:①∠3=∠4;或∠7=∠8;或∠1=∠5;或∠2=∠6;
②OP⊥AB;③AC=BC.
证明②:∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°.
在Rt△OAP与Rt△OBP中,
∵,
∴△OAP≌△OBP(HL),
∴PA=PB,∠3=∠4,
∴OP⊥AB.
14.解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,
连接FO,AO,OG,CO,OM,DO,OE,
四边形ABCD的面积为:
S四边形ABCD=×EO×AD+OM×DC+GO×BC+FO×AB
=EO(AD+AB+BC+DC)
=EO×24
=24,
解得:EO=2.
故r=2.
15.解:(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°,⑤PC2=PA PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=CD=6.
∵tan∠CPO=,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=,
∴
∴OC=3,
∴OP==15.
16.(1)证明:根据切线长定理可知:
∵∠OAE+∠ODA=(∠BAD+∠ADC)=90°,
∴∠AOD=90°,
∵∠OAE=∠OAE,∠AOD=∠AEO=90°,
∴△AOE∽△ADO,
∴=,
即AO2=AE AD;
(2)解:在Rt△AOD中,
OD==3(cm),
∵S△AOD=×AD×EO=×AO×OD
即5×EO=4×3,
∴EO=(cm),
∵OE是⊙O的半径,
∴S圆O=πr2=π(cm2).
17.解:连接OC,OD.
∵AB=18,∴OA=OB=9,
∵AC和BD是它的两条切线,
∴OA⊥AC,OB⊥BD,
∴AC∥BD,
∴∠ACD+∠BDE=180°,
∴∠OCD+∠ODC=90°,
∵AC=x,BD=y,
∴OC=,OD=,
∵CD是圆O的切线,
∴CE=AC=x,DE=BD=y,
∴OC2+OD2=CD2,
即x2+81+y2+81=(x+y)2,
整理得2xy=162,
∴xy=81.
18.(1)证明:连接CD,由AC是直径知CD⊥AB;
DE、CE都是切线,所以DE=CE,∠EDC=∠ECD;
又∠B+∠ECD=90°,∠BDE+∠EDC=90°;
所以∠B=∠BDE,所以BE=DE,从而BE=CE;
(2)解:连接OD,
当以O、D、E、C为顶点的四边形是正方形时,DE=EC=OC=OD=r;
从而BE=r,即△ABC是一个等腰直角三角形;
AC=AB=2r,S△ABC=2r2;
(3)解:若EC=4,BD=4,则BC=8;
在Rt△BDC中,cos∠CBD==;所以∠CBD=30°;
在Rt△ABC中,=tan30°,即AC=BCtan30°=8×=,OC==;
另解:设OC=r,AD=x;由EC=4,BD=4得BC=8,DC=4;
则:,解得;即OC=.
19.(1)证明:连接BD.
由于ED、EB是⊙O的切线,由切线长定理,得
ED=EB,∠DEO=∠BEO,
∴OE垂直平分BD.
又∵AB是⊙O的直径,
∴AD⊥BD.
∴AD∥OE.
即OE∥AC.
又O为AB的中点,
∴OE为△ABC的中位线,
∴BE=EC,
∴EB=EC=ED.(4分)
(2)解:在△DEC中,由于ED=EC,
∴∠C=∠CDE,
∴∠DEC=180°﹣2∠C.
①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F
满足条件.
在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求.
这是因为:
在△DCE和△DEF中,
∠CDE=∠EDF,∠C=∠DEF,
∴△DEF∽△DCE.
∴DE2=DF DC.
即(BC)2=DF DC
∴BC2=4DF DC.(6分)
②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°,
此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DF DC.(7分)
③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点
F在DC的延长线上,故线段DC上不存在满足条件的点F.(8分)
20.(1)证明:如图1,连接OB,延长AO交⊙O于点D,
∵PA,PB是⊙O的切线,A,B为切点,
∴∠OBP=∠OAP=90°,
∴∠P+∠AOB=180°,
∵∠AOB+∠BOD=180°,
∴∠BOD=∠P,
∵∠COA=∠P,
∴∠COA=∠BOD,
∵OB=OC,
∴∠BCO=∠CBO,
∵∠COB+2∠BCO=180°,∠COB+2∠COA=180°,
∴∠COA=∠BCO,
∴BC∥OA;
(2)解:如图2,延长BC交PA于点E,过点O作OF⊥BC于F,
∴BF=CF=BC=5,
∵OC=OA=13,
由勾股定理得:AE=OF==12,
∵PA,PB是⊙O的切线,A,B为切点,
∴PA=PB,
设PA=x,则PB=x,PE=x﹣12,
∵BC∥OA,OA⊥PA,
∴BE⊥PA,
∴∠PEB=90°,
∴PB2=PE2+BE2,
∴x2=(x﹣12)2+(13+5)2,
解得:x=,
∴PA=.
1.已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
2.已知:AB为⊙O的直径,∠BAD=∠B=90°,DE与⊙O相切于E,⊙O的半径为,AD=2.
①求BC的长;
②延长AE交BC的延长线于G点,求EG的长.
3.如图,P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B,C是上的任意一点,过点C的切线分别交PA、PB于点D、E.
(1)若PA=4,求△PED的周长;
(2)若∠P=40°,求∠AFB的度数.
4.如图,PA,PB分别与⊙O相切于点A,B,AC为弦,BC为⊙O的直径,若∠P=60°,PB=2cm.
(1)求证:△PAB是等边三角形;
(2)求AC的长.
5.如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PQ⊥PA,PQ交OC的延长线于点Q.
(1)求证:OQ=PQ;
(2)连BC并延长交PQ于点D,PA=AB,且CQ=6,求BD的长.
6.如图,AB、BC、CD分别与⊙O相切于E、F、G,且AB∥CD,BO=6,CO=8.
(1)判断△OBC的形状,并证明你的结论;
(2)求BC的长;
(3)求⊙O的半径OF的长.
7.如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.
8.如图,PA,PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=60°.
(1)求∠BAC的度数;
(2)当OA=2时,求AB的长.
9.如图,PA、PB分别与⊙O相切于点A、B,PO的延长线交⊙O于点C,连接BC,OA.
(1)求证:∠POA=2∠PCB;
(2)若OA=3,PA=4,求tan∠PCB的值.
10.如图,圆O是边长为6的正方形ABCD的内切圆,EF切圆O于P点,交AB、BC于点E,F,求△BEF的周长.
11.如图,已知直径与等边三角形ABC的高相等的圆与AB和BC边相切于点D和E,与AC边相交于点F和G,求∠DEF的度数.
12.已知:PA、PB、CD分别切⊙O于A、B、E三点,PA=6.求:
(1)△PCD的周长;
(2)若∠P=50°,求∠COD的度数.
13.如图所示,PA,PB是⊙O的两条切线,A,B为切点,连接PO,交⊙O于点D,交AB于点C,根据以上条件,请写出三个你认为正确的结论,并对其中的一个结论给予证明.
14.已知四边形ABCD外切于⊙O,四边形ABCD的面积为24,周长24,求⊙O的半径.
15.如图,已知:射线PO与⊙O交于A、B两点,PC、PD分别切⊙O于点C、D.
(1)请写出两个不同类型的正确结论;
(2)若CD=12,tan∠CPO=,求PO的长.
16.如图,在梯形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(1)求证:AO2=AE AD;
(2)若AO=4cm,AD=5cm,求⊙O的面积.
17.如图,⊙O的直径AB=18,AC和BD是它的两条切线,CD与⊙O相切于E,且与AC、BD相交于点C、D,设
AC=x,BD=y,试求xy的值.
18.如图,Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E;
(1)求证:BE=CE;
(2)若以O、D、E、C为顶点的四边形是正方形,⊙O的半径为r,求△ABC的面积;
(3)若EC=4,BD=,求⊙O的半径OC的长.
19.已知:以Rt△ABC的直角边AB为直径作⊙O,与斜边AC交于点D,过点D作⊙O的切线交BC边于点E.
(1)如图,求证:EB=EC=ED;
(2)试问在线段DC上是否存在点F,满足BC2=4DF DC?若存在,作出点F,并予以证明;若不存在,请说明理由.
20.如图1,PA,PB是⊙O的切线,A,B为切点,C为上的一点,∠COA=∠P.
(1)求证:BC∥OA;
(2)如图2,若BC=10,OA=13,求PA的长.
参考答案
1.解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
2.解:①过点D作DF⊥BC于点F,
∵AB为⊙O的直径,∠BAD=∠B=90°,
∴四边形ABFD是矩形,AD与BC是⊙O的切线,
∴DF=AB=2,BF=AD=2,
∵DE与⊙O相切,
∴DE=AD=2,CE=BC,
设BC=x,
则CF=BC﹣BF=x﹣2,DC=DE+CE=2+x,
在Rt△DCF中,DC2=CF2+DF2,
即(2+x)2=(x﹣2)2+(2)2,
解得:x=,
即BC=;
②∵AB为⊙O的直径,∠BAD=∠B=90°,
∴AD∥BC,
∴△ADE∽△GCE,
∴AD:CG=DE:CE,AE:EG=AD:CG,
∵AD=DE=2,
∴CG=CE=BC=,
∴BG=BC+CG=5,
∴AE:EG=4:5,
在Rt△ABG中,AG==3,
∴EG=AG=.
3.解:(1)∵DA,DC都是圆O的切线,
∴DC=DA,
同理EC=EB,
∵P是⊙O外的一点,PA、PB分别与⊙O相切于点A、B
∴PA=PB,
∴三角形PDE的周长=PD+PE+DE=PD+DC+PE+BE=PA+PB=2PA=8,
即三角形PDE的周长是8;
(2)连接AB,
∵PA=PB,
∴∠PAB=∠PBA,
∵∠P=40°,
∴∠PAB=∠PBA=(180﹣40)=70°,
∵BF⊥PB,BF为圆直径
∴∠ABF=∠PBF=90°﹣70°=20°
∴∠AFB=90°﹣20°=70°.
答:(1)若PA=4,△PED的周长为8;
(2)若∠P=40°,∠AFB的度数为70°.
4.解:(1)∵PA,PB分别与⊙O相切于点A,B,
∴PA=PB,且∠P=60°,
∴△PAB是等边三角形;
(2)∵△PAB是等边三角形;
∴PB=AB=2cm,∠PBA=60°,
∵BC是直径,PB是⊙O切线,
∴∠CAB=90°,∠PBC=90°,
∴∠ABC=30°,
∴tan∠ABC==,
∴AC=2×=cm.
5.(1)证明:连接OP.
∵PA、PC分别与⊙O相切于点A,C,
∴PA=PC,OA⊥PA,
∵OA=OC,OP=OP,
∴△OPA≌△OPC(SSS),
∴∠AOP=∠POC,
∵QP⊥PA,
∴QP∥BA,
∴∠QPO=∠AOP,
∴∠QOP=∠QPO,
∴OQ=PQ.
(2)设OA=r.
∵OB=OC,
∴∠OBC=∠OCB,
∵OB∥QD,
∴∠QDC=∠B,
∵∠OCB=∠QCD,
∴∠QCD=∠QDC,
∴QC=QD=6,∵QO=QP,
∴OC=DP=r,
∵PC是⊙O的切线,
∴OC⊥PC,
∴∠OCP=∠PCQ=90°,
在Rt△PCQ中,∵PQ2=PC2+QC2,
∴(6+r)2=62+(2r)2,
r=4或0(舍弃),
∴OP==4,
∵OB=PD,OB∥PD,
∴四边形OBDP是平行四边形,
∴BD=OP=4.
6.(1)答:△OBC是直角三角形.
证明:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴∠OBE=∠OBF=∠EBF,∠OCG=∠OCF=∠GCF,
∵AB∥CD,
∴∠EBF+∠GCF=180°,
∴∠OBF+∠OCF=90°,
∴∠BOC=90°,
∴△OBC是直角三角形;
(2)解:∵在Rt△BOC中,BO=6,CO=8,
∴BC==10;
(3)解:∵AB、BC、CD分别与⊙O相切于E、F、G,
∴OF⊥BC,
∴OF===4.8.
7.解:设AF=x,
∵四边形ABCD是正方形,
∴∠DAB=90°,
∴DA⊥AB,
∴AD是圆的切线,
∵CF是⊙O的切线,E为切点,
∴EF=AF=x,
∴FD=1﹣x,
∵CB⊥AB,
∴CB 为⊙O 的切线,
∴CB=CE,
∴CF=CE+EF=CB+EF=1+x.
∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,
即(1+x)2=1+(1﹣x)2,
解得x=,
∴DF=1﹣x=,
∴S△CDF=×1×=.
8.解:(1)∵PA,PB是⊙O的切线,
∴AP=BP,
∵∠P=60°,
∴∠PAB=60°,
∵AC是⊙O的直径,
∴∠PAC=90°,
∴∠BAC=90°﹣60°=30°.
(2)连接OP,则在Rt△AOP中,OA=2,∠APO=30°,
∴OP=4,
由勾股定理得:,
∵AP=BP,∠APB=60°,
∴△APB是等边三角形,
∴.
9.证明:(1)连接OB,
∵PA、PB分别与⊙O相切于点A、B,
∴PA=PB,∠OBP=∠OAP=90°,
在Rt△POA和Rt△POB中,
∵,
∴Rt△POA≌Rt△POB(HL),
∴∠POA=∠POB,
∵∠POB=2∠PCB,
∴∠POA=2∠PCB;
(2)过B作BE⊥PC于E,
∵PB=PA=4,OB=OA=3,
∴PO=5,
∴PO BE=OB PB,
∴BE=,
由勾股定理得:OE==,
∴CE=OC+OE=3+=,
在Rt△OBE中,tan∠PCB===.
10.解:设⊙O切AB于M,切BC于N,连接OM、ON,
则∠OMB=∠ONB=90°,
∵四边形ABCD是正方形,
∴∠B=90°,
∵ON=OM,
∴四边形MBNO是正方形,
∵圆O是边长为6的正方形ABCD的内切圆,
∴BM=BN=OM=ON=AB=×6=3,
由切线长定理得:EM=EP,PF=FN,
∴△BEF的周长为BF+EF+BE
=BF+PF+PE+BE
=BF+FN+EM+BE
=BN+BM
=3+3
=6.
11.解:过点E作BC的垂线与圆交于点H,与AC交于点O.
连接AH和DH,作AM⊥BC,垂足为M.
∵E为切点,∴EH必过圆心,即EH是直径,
∴DH⊥DE,
∵D、E是切点,∴BD=BE,
∵∠B=60°,∴△DBE是正三角形,
∴∠BDE=∠BAC=60°,
∴DE∥AC,DH⊥AC,
由已知得,AM=EH,又AM∥EH,∴四边形AMEH是矩形,
∴AH⊥HE,即AH是切线,
∴AD=AH,AC垂直平分DH,AC必过圆心,
∴AC与EH的交点O是圆心,
∴OE=OF,
∵∠COE=90°﹣∠C=30°,∴∠OEF=75°,
∵∠DEO=∠EOC=30°,
∴∠DEF=30°+75°=105°
法二:过点E作BC的垂线与圆交于点H,与AC交于点O.
∵BC为切线
∴O为圆心,OE⊥BC.
∵OE=OF
∴∠OFE=∠OEF.
∴∠OEF=∠C+∠FEC,∠FEC=∠OEF﹣∠C
又∵∠OEC=90°,
∴∠OEF+∠FEC=90°
即2∠OEF﹣∠C=90°.
∵∠C=60°,
∴∠OEF=75°,∠CEF=15°.
又∵AC∥DE,∠C=60°,
∴∠DEC=120°.
∵∠CEF=15°,
∴∠DEF=105°
12.解:(1)∵PA、PB切⊙O于A、B,CD切⊙O于E,
∴PA=PB=6,ED=BD,CE=AC;
∴△PCD的周长=PD+DE+PC+CE=2PA=12;
(2)连接OE,如图所示:
由切线的性质得,OA⊥PA,OB⊥PB,OE⊥CD,
∴∠OAC=∠OEC=∠OED=∠OBD=90°,
∴∠AOB+∠P=180°,
∴∠AOB=180°﹣∠P=130°,
由切线长定理得:∠AOC=∠EOC,∠EOD=∠BOD,
∴∠COD=∠AOB=×130°=65°.
13.解:如图所示,结论:①∠3=∠4;或∠7=∠8;或∠1=∠5;或∠2=∠6;
②OP⊥AB;③AC=BC.
证明②:∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠OAP=∠OBP=90°.
在Rt△OAP与Rt△OBP中,
∵,
∴△OAP≌△OBP(HL),
∴PA=PB,∠3=∠4,
∴OP⊥AB.
14.解:设四边形ABCD是⊙O的外切四边形,切点分别为:F,G,M,E,
连接FO,AO,OG,CO,OM,DO,OE,
四边形ABCD的面积为:
S四边形ABCD=×EO×AD+OM×DC+GO×BC+FO×AB
=EO(AD+AB+BC+DC)
=EO×24
=24,
解得:EO=2.
故r=2.
15.解:(1)不同类型的正确结论有:
①PC=PD,②∠CPO=∠DPA,③CD⊥BA,④∠CEP=90°,⑤PC2=PA PB;
(2)连接OC
∵PC、PD分别切⊙O于点C、D
∴PC=PD,∠CPO=∠DPA
∴CD⊥AB
∵CD=12
∴DE=CE=CD=6.
∵tan∠CPO=,
∴在Rt△EPC中,PE=12
∴由勾股定理得CP=6
∵PC切⊙O于点C
∴∠OCP=90°
在Rt△OPC中,
∵tan∠CPO=,
∴
∴OC=3,
∴OP==15.
16.(1)证明:根据切线长定理可知:
∵∠OAE+∠ODA=(∠BAD+∠ADC)=90°,
∴∠AOD=90°,
∵∠OAE=∠OAE,∠AOD=∠AEO=90°,
∴△AOE∽△ADO,
∴=,
即AO2=AE AD;
(2)解:在Rt△AOD中,
OD==3(cm),
∵S△AOD=×AD×EO=×AO×OD
即5×EO=4×3,
∴EO=(cm),
∵OE是⊙O的半径,
∴S圆O=πr2=π(cm2).
17.解:连接OC,OD.
∵AB=18,∴OA=OB=9,
∵AC和BD是它的两条切线,
∴OA⊥AC,OB⊥BD,
∴AC∥BD,
∴∠ACD+∠BDE=180°,
∴∠OCD+∠ODC=90°,
∵AC=x,BD=y,
∴OC=,OD=,
∵CD是圆O的切线,
∴CE=AC=x,DE=BD=y,
∴OC2+OD2=CD2,
即x2+81+y2+81=(x+y)2,
整理得2xy=162,
∴xy=81.
18.(1)证明:连接CD,由AC是直径知CD⊥AB;
DE、CE都是切线,所以DE=CE,∠EDC=∠ECD;
又∠B+∠ECD=90°,∠BDE+∠EDC=90°;
所以∠B=∠BDE,所以BE=DE,从而BE=CE;
(2)解:连接OD,
当以O、D、E、C为顶点的四边形是正方形时,DE=EC=OC=OD=r;
从而BE=r,即△ABC是一个等腰直角三角形;
AC=AB=2r,S△ABC=2r2;
(3)解:若EC=4,BD=4,则BC=8;
在Rt△BDC中,cos∠CBD==;所以∠CBD=30°;
在Rt△ABC中,=tan30°,即AC=BCtan30°=8×=,OC==;
另解:设OC=r,AD=x;由EC=4,BD=4得BC=8,DC=4;
则:,解得;即OC=.
19.(1)证明:连接BD.
由于ED、EB是⊙O的切线,由切线长定理,得
ED=EB,∠DEO=∠BEO,
∴OE垂直平分BD.
又∵AB是⊙O的直径,
∴AD⊥BD.
∴AD∥OE.
即OE∥AC.
又O为AB的中点,
∴OE为△ABC的中位线,
∴BE=EC,
∴EB=EC=ED.(4分)
(2)解:在△DEC中,由于ED=EC,
∴∠C=∠CDE,
∴∠DEC=180°﹣2∠C.
①当∠DEC>∠C时,有180°﹣2∠C>∠C,即0°<∠C<60°时,在线段DC上存在点F
满足条件.
在∠DEC内,以ED为一边,作∠DEF,使∠DEF=∠C,且EF交DC于点F,则点F即为所求.
这是因为:
在△DCE和△DEF中,
∠CDE=∠EDF,∠C=∠DEF,
∴△DEF∽△DCE.
∴DE2=DF DC.
即(BC)2=DF DC
∴BC2=4DF DC.(6分)
②当∠DEC=∠C时,△DEC为等边三角形,即∠DEC=∠C=60°,
此时,C点即为满足条件的F点,于是,DF=DC=DE,仍有BC2=4DE2=4DF DC.(7分)
③当∠DEC<∠C时,即180°﹣2∠C<∠C,60°<∠C<90°;所作的∠DEF>∠DEC,此时点
F在DC的延长线上,故线段DC上不存在满足条件的点F.(8分)
20.(1)证明:如图1,连接OB,延长AO交⊙O于点D,
∵PA,PB是⊙O的切线,A,B为切点,
∴∠OBP=∠OAP=90°,
∴∠P+∠AOB=180°,
∵∠AOB+∠BOD=180°,
∴∠BOD=∠P,
∵∠COA=∠P,
∴∠COA=∠BOD,
∵OB=OC,
∴∠BCO=∠CBO,
∵∠COB+2∠BCO=180°,∠COB+2∠COA=180°,
∴∠COA=∠BCO,
∴BC∥OA;
(2)解:如图2,延长BC交PA于点E,过点O作OF⊥BC于F,
∴BF=CF=BC=5,
∵OC=OA=13,
由勾股定理得:AE=OF==12,
∵PA,PB是⊙O的切线,A,B为切点,
∴PA=PB,
设PA=x,则PB=x,PE=x﹣12,
∵BC∥OA,OA⊥PA,
∴BE⊥PA,
∴∠PEB=90°,
∴PB2=PE2+BE2,
∴x2=(x﹣12)2+(13+5)2,
解得:x=,
∴PA=.
