2021-2022学年沪科版数学八年级下册 17.5 一元二次方程的应用 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学八年级下册 17.5 一元二次方程的应用 同步练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 268.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览



文档简介
绝密★启用前
17.5一元二次方程的应用同步练习
沪科版版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
如图,在宽为米,长为米的矩形地面上修建两条同样宽的道路,余下部分作为耕地,若耕地面积需要平方米,则修建的路宽应为
A. 米
B. 米
C. 米
D. 米
某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了条航线,则这个航空公司共有飞机场
A. 个 B. 个 C. 个 D. 个
股票每天的涨幅、跌幅均不能超过,即当涨了原价的后,便不能再涨,叫做涨停当跌了原价的后,便不能再跌,叫做跌停现有一只股票某天跌停,之后两天时间又涨回到原价设这两天此股票股价的平均增长率为,则满足的方程是
A. B.
C. D.
某种植基地年蔬菜产量为吨,预计年蔬菜产量达到吨,求蔬菜产量的年平均增长率设蔬菜产量的年平均增长率为,则可列方程为
A. B.
C. D.
某商店以每件元的价格购进一批商品,物价局限定,每件商品的利润不得超过,若每件商品售价定为元,则可卖出件,商店预期要盈利元,那么每件商品的售价应定为
A. 元 B. 元 C. 元或元 D. 元
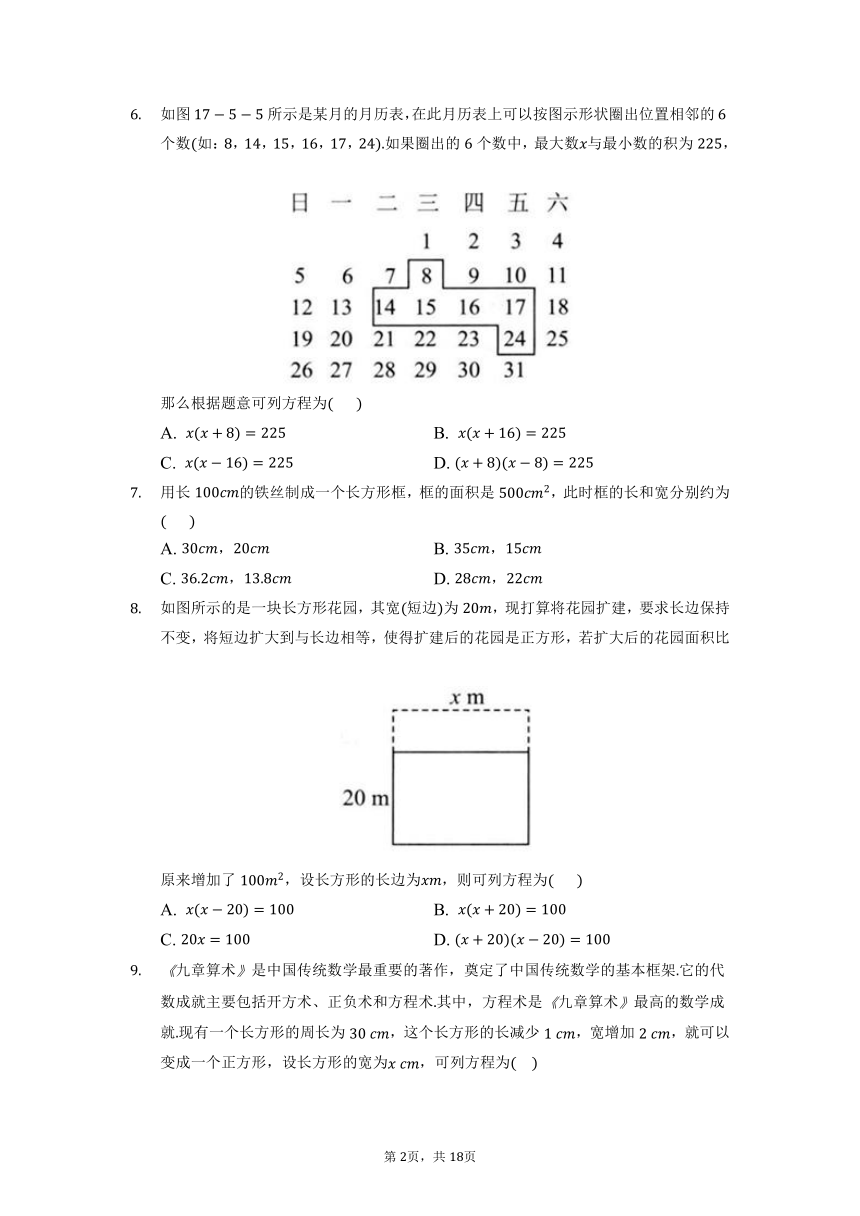
如图所示是某月的月历表,在此月历表上可以按图示形状圈出位置相邻的个数如:,,,,,如果圈出的个数中,最大数与最小数的积为,那么根据题意可列方程为
A. B.
C. D.
用长的铁丝制成一个长方形框,框的面积是,此时框的长和宽分别约为
A. , B. ,
C. , D. ,
如图所示的是一块长方形花园,其宽短边为,现打算将花园扩建,要求长边保持不变,将短边扩大到与长边相等,使得扩建后的花园是正方形,若扩大后的花园面积比原来增加了,设长方形的长边为,则可列方程为
A. B.
C. D.
九章算术是中国传统数学最重要的著作,奠定了中国传统数学的基本框架它的代数成就主要包括开方术、正负术和方程术其中,方程术是九章算术最高的数学成就现有一个长方形的周长为,这个长方形的长减少,宽增加,就可以变成一个正方形,设长方形的宽为,可列方程为
A. B.
C. D.
新年来临之际,某班全体同学互赠新年贺卡,共赠贺卡张,设全班共有名学生,那么根据题意可列方程
A. B.
C. D.
新冠肺炎疫情期间,某社区卡口有志愿者轮流值班,每人一班,每小时换班一次,如果其中有两人同值一班后,到下次两人再同班,最长需要的天数是天,那么这个社区卡口的志愿者有
A. 人 B. 人 C. 人 D. 人
如图,在一幅长为,宽为的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是,设金色纸边的宽为,那么满足的方程为
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
如图,学校课外生物小组的试验园地的形状是长、宽的矩形为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为,则小道的宽为多少米若设小道的宽为,则根据题意,可列方程为 .
如图,在中,,,为边上的高,动点从点出发,沿方向以的速度向点运动设的面积为,矩形的面积为,运动时间为,则 时,.
如图是一张长,宽的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分阴影部分可制成底面积是的有盖的长方体铁盒则剪去的正方形的边长为 .
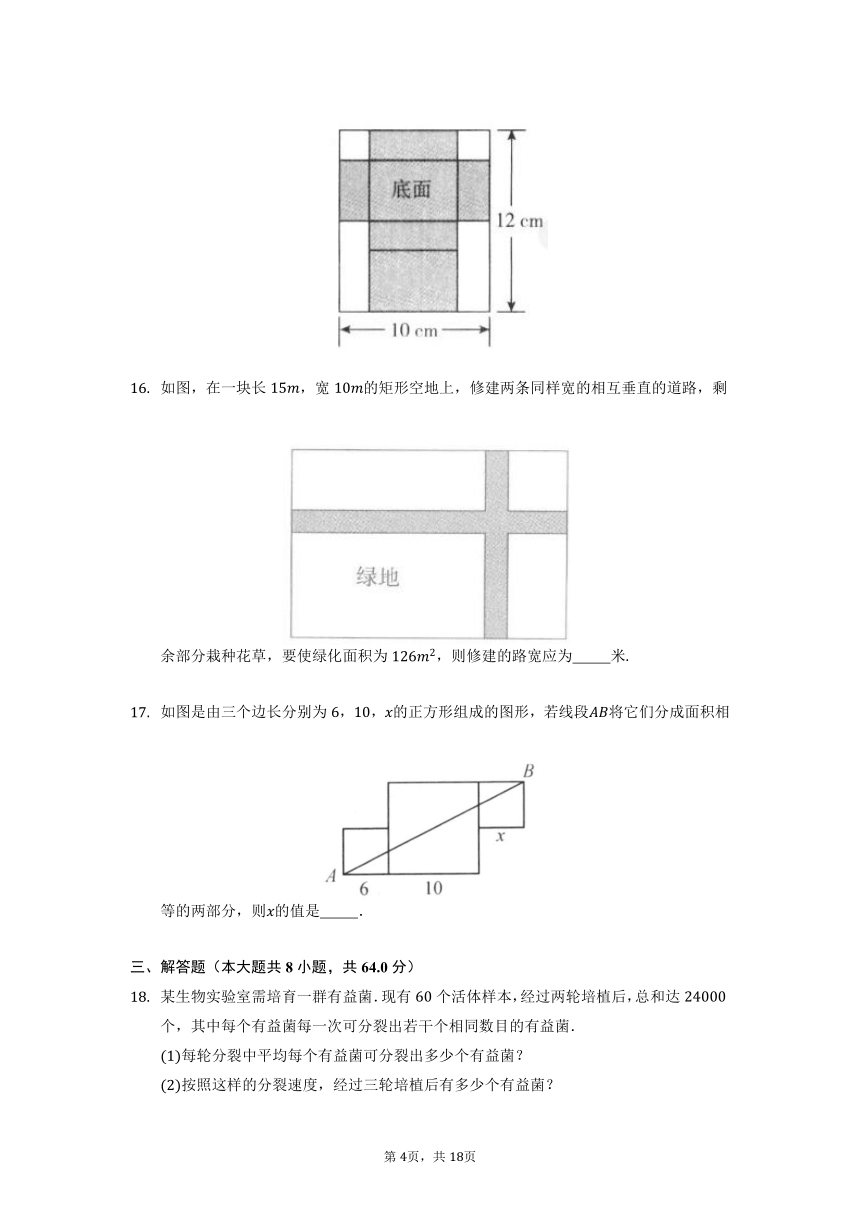
如图,在一块长,宽的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种花草,要使绿化面积为,则修建的路宽应为 米
如图是由三个边长分别为,,的正方形组成的图形,若线段将它们分成面积相等的两部分,则的值是 .
三、解答题(本大题共8小题,共64.0分)
某生物实验室需培育一群有益菌.现有个活体样本,经过两轮培植后,总和达个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
每轮分裂中平均每个有益菌可分裂出多少个有益菌?
按照这样的分裂速度,经过三轮培植后有多少个有益菌?
青海新闻网讯:年月日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了万元,建成个公共自行车站点、配置辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计年将投资万元,新建个公共自行车站点、配置辆公共自行车.
请问每个站点的造价和公共自行车的单价分别是多少万元?
请你求出年到年市政府配置公共自行车数量的年平均增长率.
新学期开始时,某校九年级一班的同学为了增添教室绿色文化,准备到一家植物种植基地购买、两种花苗据了解,购买种花苗盆,种花苗盆,需元购买种花苗盆,种花苗盆,需元.
求、两种花苗的单价分别是多少元
经九年级一班班委会商定,决定购买、两种花苗共盆进行搭配装扮教室种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少盆种花苗,种花苗每盆就降价多少元若九年级一班的同学本次购买花苗共花费了元,请计算出本次购买了、两种花苗各多少盆.
如图,要利用一面墙墙长为,用的围栏建羊圈,基本结构为三个大小相同的矩形.
如果围成的总面积为,求羊圈的边,的长各为多少
保持羊圈的基本结构,羊圈总面积是否可以达到请说明理由.
某博物馆每周都吸引大量中外游客前来参观如果游客过多,对馆中的珍贵文物会产生不利影响,因此博物馆采取了提高门票价格的方法来控制参观人数,在该方法的实施过程中发现:每周参观人数人与票价元之间存在着如图所示的一次函数关系,在这种情况下,如果要保证每周万元的门票收入,那么每周应限定参观人数为多少门票价格应是多少
一家水果店以每斤元的价格购进某种水果若干斤,然后以每斤元的价格出售,每天可售出斤,通过调查发现,这种水果每斤的售价每降低元,每天可多售出斤.
若将这种水果每斤的售价降低元,则每天的销售量是多少斤用含的代数式表示
销售这种水果要想每天盈利元,且保证每天至少售出斤,那么水果店需将每斤的售价降低多少元
山西特产专卖店销售核桃,其进价为每千克元按每千克元出售,平均每天可售出千克后来经过市场调查发现,单价每降低元,则平均每天的销售量可增加千克若该专卖店销售这种核桃要想平均每天获利元请回答:
每千克核桃应降价多少元
在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应该按原售价的几折出售
某桶装水经营部每天的房租、人员工资等固定成本为元,每桶水的进价是元,规定销售单价不得高于元,也不得低于元,经调查发现日均销售量桶与销售单价元的函数图象如图所示.
求日均销售量桶与销售单价元的函数表达式
若该经营部希望日均获利元,请你根据以上信息,就该桶装水的销售单价或日均销售量,提出一个用一元二次方程解决的问题,并写出解答过程.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.要求修建的路宽,就要设修建的路宽应为米,根据题意列出等量关系解方程即可.
【解答】
解:设修建的路宽应为米,
根据等量关系列方程得:,
解得:或,
不合题意,舍去,
故选A.
2.【答案】
【解析】解:设这个航空公司共有飞机场个.
,
解得,不合题意,舍去.
答:这个航空公司共有飞机场个.
故选:.
每个飞机场都要与其余的飞机场开辟一条航行,但两个飞机场之间只开通一条航线.等量关系为:飞机场数飞机场数,列方程并解方程即可.
此题考查一元二次方程的应用;得到飞行总航线与飞机场数的等量关系是解决本题的关键.
3.【答案】
【解析】略
4.【答案】
【解析】
【分析】
此题考查了一元二次方程的应用增长率问题解题的关键在于理清题目的含义,找到年和年的产量的代数式,根据条件找准等量关系式,列出方程.利用增长后的量增长前的量增长率,设平均每次增长的百分率为,根据“从吨增加到吨”,即可得出方程.
【解答】
解:由题意知,蔬菜产量的年平均增长率为,
根据年蔬菜产量为吨,则年蔬菜产量为吨,年蔬菜产量为吨,预计年蔬菜产量达到吨,
即:或.
故选C.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】解:设这个社区卡口共有位志愿者,每人一班,轮流值班,则有种组合,一天是小时,小时班,每天个班,所以总组合数除以可得出最长需要的天数,
则,
解得舍去,,
故选C.
12.【答案】
【解析】解:结合题图可得,挂图长为,宽为,
由矩形的面积公式得,整理得.
故选B.
13.【答案】
【解析】略
14.【答案】
【解析】在中, ,,为边上的高,.
又,
,.
易知,
.
,
解得舍去,.
15.【答案】
【解析】解:设底面长为,宽为,正方形的边长为,根据题意
得
,,
代入中,得,
整理得,
解得或舍去,
故剪去的正方形的边长为.
16.【答案】
【解析】解:设道路的宽为,由题意得,解得,不合题意,舍去,则道路的宽应为米.
17.【答案】或
【解析】解:如图所示,延长,交于点,延长,交于点,则四边形是矩形,
与面积相等.
又线段将三个正方形分成面积相等的两部分,
矩形与矩形的面积相等.
,解得或.
故答案为或.
18.【答案】解:设每轮分裂中平均每个有益菌可分裂出个有益菌,
由题意,得,
,
解得:,舍去,
.
答:每轮分裂中平均每个有益菌可分裂出个有益菌.
由题意,得个.
答:经过三轮培植后有个有益菌.
【解析】本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时分别表示出每轮分解后的总数是关键.
设每轮分裂中平均每个有益菌可分裂出个有益菌,则第一轮分裂后有个,第二轮分裂出,两次加起来共有建立方程求出其解就可以;
根据的结论,就可以得出第三轮共有个有益菌,将的值代入就可以得出结论.
本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时分别表示出每轮分解后的总数是关键.
19.【答案】解:设每个站点造价万元,自行车单价为万元.
根据题意可得:
解得:
答:每个站点造价为万元,自行车单价为万元.
设年到年市政府配置公共自行车数量的年平均增长率为.
根据题意可得:
解此方程:,
即:,不符合题意,舍去
答:年到年市政府配置公共自行车数量的年平均增长率为.
【解析】此题主要考查了二元一次方程的应用以及一元二次方程的应用,正确得出等式是解题关键.
分别利用投资了万元,建成个公共自行车站点、配置辆公共自行车以及投资万元,新建个公共自行车站点、配置辆公共自行车列出二元一次方程组,解方程组求出答案;
利用年配置辆公共自行车,结合增长率为,进而表示出年配置公共自行车数量,得出等式求出答案.
20.【答案】解:设种花苗的单价为元,种花苗的单价为元,
依题意得
解得
答:种花苗的单价为元,种花苗的单价为元.
设购买种花苗盆,则购买种花苗盆,
依题意得,
整理得,
解得,,
当时,
当时,.
答:购买了种花苗盆,种花苗盆或购买了种花苗盆,种花苗盆.
【解析】见答案
21.【答案】设,则,
,
.
由题意知,,即,
解得,舍,
,.
答:羊圈的边长为,长为.
不能.
理由:设时,羊圈总面积可以达到,
由题意,得,
即,
,,,
,
方程无实数根,
羊圈总面积不可能达到.
【解析】见答案
22.【答案】解:设每周参观人数人与票价元之间的一次函数关系式为,
根据题意,得
解得
.
,
即,
,
解得,.
当时,,
当时,.
要控制参观人数,
取,此时.
答:每周应限定参观人数为人,门票价格应是元.
【解析】见答案
23.【答案】每天的销售量是斤
水果店需将每斤的售价降低元
【解析】略
24.【答案】解:设每千克核桃应降价元.
根据题意,得.
化简,得.
解得,.
答:每千克核桃应降价元或元.
由可知每千克核桃可降价元或元.
因为要尽可能让利于顾客,所以每千克核桃应降价元.
此时,售价为元,
所以.
答:该店应该按原售价的九折出售.
【解析】设出未知数,利用“平均每天的销售量每千克的利润元”列出方程求解即可.
25.【答案】解:结合题图可设日均销售量桶与销售单价元的函数表达式为,
根据题意得
解得
所以日均销售量桶与销售单价元的函数表达式为.
所提问题不唯一如:“若该经营部希望日均获利元,那么日均应销售多少桶水”
根据题意得,
解得,不合题意,舍去,
当时,.
答:若该经营部希望日均获利元,那么日均应销售桶水.
【解析】本题考查了一元二次方程及一次函数的应用,解题的关键是通过题目和图象建立合适的函数模型求解.
第2页,共2页
第1页,共1页
17.5一元二次方程的应用同步练习
沪科版版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
如图,在宽为米,长为米的矩形地面上修建两条同样宽的道路,余下部分作为耕地,若耕地面积需要平方米,则修建的路宽应为
A. 米
B. 米
C. 米
D. 米
某航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了条航线,则这个航空公司共有飞机场
A. 个 B. 个 C. 个 D. 个
股票每天的涨幅、跌幅均不能超过,即当涨了原价的后,便不能再涨,叫做涨停当跌了原价的后,便不能再跌,叫做跌停现有一只股票某天跌停,之后两天时间又涨回到原价设这两天此股票股价的平均增长率为,则满足的方程是
A. B.
C. D.
某种植基地年蔬菜产量为吨,预计年蔬菜产量达到吨,求蔬菜产量的年平均增长率设蔬菜产量的年平均增长率为,则可列方程为
A. B.
C. D.
某商店以每件元的价格购进一批商品,物价局限定,每件商品的利润不得超过,若每件商品售价定为元,则可卖出件,商店预期要盈利元,那么每件商品的售价应定为
A. 元 B. 元 C. 元或元 D. 元
如图所示是某月的月历表,在此月历表上可以按图示形状圈出位置相邻的个数如:,,,,,如果圈出的个数中,最大数与最小数的积为,那么根据题意可列方程为
A. B.
C. D.
用长的铁丝制成一个长方形框,框的面积是,此时框的长和宽分别约为
A. , B. ,
C. , D. ,
如图所示的是一块长方形花园,其宽短边为,现打算将花园扩建,要求长边保持不变,将短边扩大到与长边相等,使得扩建后的花园是正方形,若扩大后的花园面积比原来增加了,设长方形的长边为,则可列方程为
A. B.
C. D.
九章算术是中国传统数学最重要的著作,奠定了中国传统数学的基本框架它的代数成就主要包括开方术、正负术和方程术其中,方程术是九章算术最高的数学成就现有一个长方形的周长为,这个长方形的长减少,宽增加,就可以变成一个正方形,设长方形的宽为,可列方程为
A. B.
C. D.
新年来临之际,某班全体同学互赠新年贺卡,共赠贺卡张,设全班共有名学生,那么根据题意可列方程
A. B.
C. D.
新冠肺炎疫情期间,某社区卡口有志愿者轮流值班,每人一班,每小时换班一次,如果其中有两人同值一班后,到下次两人再同班,最长需要的天数是天,那么这个社区卡口的志愿者有
A. 人 B. 人 C. 人 D. 人
如图,在一幅长为,宽为的矩形风景画的四周镶一条宽度相同的金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是,设金色纸边的宽为,那么满足的方程为
A. B.
C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
如图,学校课外生物小组的试验园地的形状是长、宽的矩形为便于管理,要在中间开辟一横两纵共三条等宽的小道,使种植面积为,则小道的宽为多少米若设小道的宽为,则根据题意,可列方程为 .
如图,在中,,,为边上的高,动点从点出发,沿方向以的速度向点运动设的面积为,矩形的面积为,运动时间为,则 时,.
如图是一张长,宽的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分阴影部分可制成底面积是的有盖的长方体铁盒则剪去的正方形的边长为 .
如图,在一块长,宽的矩形空地上,修建两条同样宽的相互垂直的道路,剩余部分栽种花草,要使绿化面积为,则修建的路宽应为 米
如图是由三个边长分别为,,的正方形组成的图形,若线段将它们分成面积相等的两部分,则的值是 .
三、解答题(本大题共8小题,共64.0分)
某生物实验室需培育一群有益菌.现有个活体样本,经过两轮培植后,总和达个,其中每个有益菌每一次可分裂出若干个相同数目的有益菌.
每轮分裂中平均每个有益菌可分裂出多少个有益菌?
按照这样的分裂速度,经过三轮培植后有多少个有益菌?
青海新闻网讯:年月日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了万元,建成个公共自行车站点、配置辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计年将投资万元,新建个公共自行车站点、配置辆公共自行车.
请问每个站点的造价和公共自行车的单价分别是多少万元?
请你求出年到年市政府配置公共自行车数量的年平均增长率.
新学期开始时,某校九年级一班的同学为了增添教室绿色文化,准备到一家植物种植基地购买、两种花苗据了解,购买种花苗盆,种花苗盆,需元购买种花苗盆,种花苗盆,需元.
求、两种花苗的单价分别是多少元
经九年级一班班委会商定,决定购买、两种花苗共盆进行搭配装扮教室种植基地销售人员为了支持本次活动,为该班同学提供以下优惠:购买多少盆种花苗,种花苗每盆就降价多少元若九年级一班的同学本次购买花苗共花费了元,请计算出本次购买了、两种花苗各多少盆.
如图,要利用一面墙墙长为,用的围栏建羊圈,基本结构为三个大小相同的矩形.
如果围成的总面积为,求羊圈的边,的长各为多少
保持羊圈的基本结构,羊圈总面积是否可以达到请说明理由.
某博物馆每周都吸引大量中外游客前来参观如果游客过多,对馆中的珍贵文物会产生不利影响,因此博物馆采取了提高门票价格的方法来控制参观人数,在该方法的实施过程中发现:每周参观人数人与票价元之间存在着如图所示的一次函数关系,在这种情况下,如果要保证每周万元的门票收入,那么每周应限定参观人数为多少门票价格应是多少
一家水果店以每斤元的价格购进某种水果若干斤,然后以每斤元的价格出售,每天可售出斤,通过调查发现,这种水果每斤的售价每降低元,每天可多售出斤.
若将这种水果每斤的售价降低元,则每天的销售量是多少斤用含的代数式表示
销售这种水果要想每天盈利元,且保证每天至少售出斤,那么水果店需将每斤的售价降低多少元
山西特产专卖店销售核桃,其进价为每千克元按每千克元出售,平均每天可售出千克后来经过市场调查发现,单价每降低元,则平均每天的销售量可增加千克若该专卖店销售这种核桃要想平均每天获利元请回答:
每千克核桃应降价多少元
在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应该按原售价的几折出售
某桶装水经营部每天的房租、人员工资等固定成本为元,每桶水的进价是元,规定销售单价不得高于元,也不得低于元,经调查发现日均销售量桶与销售单价元的函数图象如图所示.
求日均销售量桶与销售单价元的函数表达式
若该经营部希望日均获利元,请你根据以上信息,就该桶装水的销售单价或日均销售量,提出一个用一元二次方程解决的问题,并写出解答过程.
答案和解析
1.【答案】
【解析】
【分析】
本题考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.要求修建的路宽,就要设修建的路宽应为米,根据题意列出等量关系解方程即可.
【解答】
解:设修建的路宽应为米,
根据等量关系列方程得:,
解得:或,
不合题意,舍去,
故选A.
2.【答案】
【解析】解:设这个航空公司共有飞机场个.
,
解得,不合题意,舍去.
答:这个航空公司共有飞机场个.
故选:.
每个飞机场都要与其余的飞机场开辟一条航行,但两个飞机场之间只开通一条航线.等量关系为:飞机场数飞机场数,列方程并解方程即可.
此题考查一元二次方程的应用;得到飞行总航线与飞机场数的等量关系是解决本题的关键.
3.【答案】
【解析】略
4.【答案】
【解析】
【分析】
此题考查了一元二次方程的应用增长率问题解题的关键在于理清题目的含义,找到年和年的产量的代数式,根据条件找准等量关系式,列出方程.利用增长后的量增长前的量增长率,设平均每次增长的百分率为,根据“从吨增加到吨”,即可得出方程.
【解答】
解:由题意知,蔬菜产量的年平均增长率为,
根据年蔬菜产量为吨,则年蔬菜产量为吨,年蔬菜产量为吨,预计年蔬菜产量达到吨,
即:或.
故选C.
5.【答案】
【解析】略
6.【答案】
【解析】略
7.【答案】
【解析】略
8.【答案】
【解析】略
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】解:设这个社区卡口共有位志愿者,每人一班,轮流值班,则有种组合,一天是小时,小时班,每天个班,所以总组合数除以可得出最长需要的天数,
则,
解得舍去,,
故选C.
12.【答案】
【解析】解:结合题图可得,挂图长为,宽为,
由矩形的面积公式得,整理得.
故选B.
13.【答案】
【解析】略
14.【答案】
【解析】在中, ,,为边上的高,.
又,
,.
易知,
.
,
解得舍去,.
15.【答案】
【解析】解:设底面长为,宽为,正方形的边长为,根据题意
得
,,
代入中,得,
整理得,
解得或舍去,
故剪去的正方形的边长为.
16.【答案】
【解析】解:设道路的宽为,由题意得,解得,不合题意,舍去,则道路的宽应为米.
17.【答案】或
【解析】解:如图所示,延长,交于点,延长,交于点,则四边形是矩形,
与面积相等.
又线段将三个正方形分成面积相等的两部分,
矩形与矩形的面积相等.
,解得或.
故答案为或.
18.【答案】解:设每轮分裂中平均每个有益菌可分裂出个有益菌,
由题意,得,
,
解得:,舍去,
.
答:每轮分裂中平均每个有益菌可分裂出个有益菌.
由题意,得个.
答:经过三轮培植后有个有益菌.
【解析】本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时分别表示出每轮分解后的总数是关键.
设每轮分裂中平均每个有益菌可分裂出个有益菌,则第一轮分裂后有个,第二轮分裂出,两次加起来共有建立方程求出其解就可以;
根据的结论,就可以得出第三轮共有个有益菌,将的值代入就可以得出结论.
本题考查了列一元二次方程解实际问题的运用,一元二次方程的解法的运用,解答时分别表示出每轮分解后的总数是关键.
19.【答案】解:设每个站点造价万元,自行车单价为万元.
根据题意可得:
解得:
答:每个站点造价为万元,自行车单价为万元.
设年到年市政府配置公共自行车数量的年平均增长率为.
根据题意可得:
解此方程:,
即:,不符合题意,舍去
答:年到年市政府配置公共自行车数量的年平均增长率为.
【解析】此题主要考查了二元一次方程的应用以及一元二次方程的应用,正确得出等式是解题关键.
分别利用投资了万元,建成个公共自行车站点、配置辆公共自行车以及投资万元,新建个公共自行车站点、配置辆公共自行车列出二元一次方程组,解方程组求出答案;
利用年配置辆公共自行车,结合增长率为,进而表示出年配置公共自行车数量,得出等式求出答案.
20.【答案】解:设种花苗的单价为元,种花苗的单价为元,
依题意得
解得
答:种花苗的单价为元,种花苗的单价为元.
设购买种花苗盆,则购买种花苗盆,
依题意得,
整理得,
解得,,
当时,
当时,.
答:购买了种花苗盆,种花苗盆或购买了种花苗盆,种花苗盆.
【解析】见答案
21.【答案】设,则,
,
.
由题意知,,即,
解得,舍,
,.
答:羊圈的边长为,长为.
不能.
理由:设时,羊圈总面积可以达到,
由题意,得,
即,
,,,
,
方程无实数根,
羊圈总面积不可能达到.
【解析】见答案
22.【答案】解:设每周参观人数人与票价元之间的一次函数关系式为,
根据题意,得
解得
.
,
即,
,
解得,.
当时,,
当时,.
要控制参观人数,
取,此时.
答:每周应限定参观人数为人,门票价格应是元.
【解析】见答案
23.【答案】每天的销售量是斤
水果店需将每斤的售价降低元
【解析】略
24.【答案】解:设每千克核桃应降价元.
根据题意,得.
化简,得.
解得,.
答:每千克核桃应降价元或元.
由可知每千克核桃可降价元或元.
因为要尽可能让利于顾客,所以每千克核桃应降价元.
此时,售价为元,
所以.
答:该店应该按原售价的九折出售.
【解析】设出未知数,利用“平均每天的销售量每千克的利润元”列出方程求解即可.
25.【答案】解:结合题图可设日均销售量桶与销售单价元的函数表达式为,
根据题意得
解得
所以日均销售量桶与销售单价元的函数表达式为.
所提问题不唯一如:“若该经营部希望日均获利元,那么日均应销售多少桶水”
根据题意得,
解得,不合题意,舍去,
当时,.
答:若该经营部希望日均获利元,那么日均应销售桶水.
【解析】本题考查了一元二次方程及一次函数的应用,解题的关键是通过题目和图象建立合适的函数模型求解.
第2页,共2页
第1页,共1页
