2021-2022学年沪科版数学八年级下册 18.1勾股定理 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年沪科版数学八年级下册 18.1勾股定理 同步练习(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 297.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 19:51:26 | ||
图片预览



文档简介
绝密★启用前
18.1 勾股定理同步练习
沪科版版初中数学八年级下册
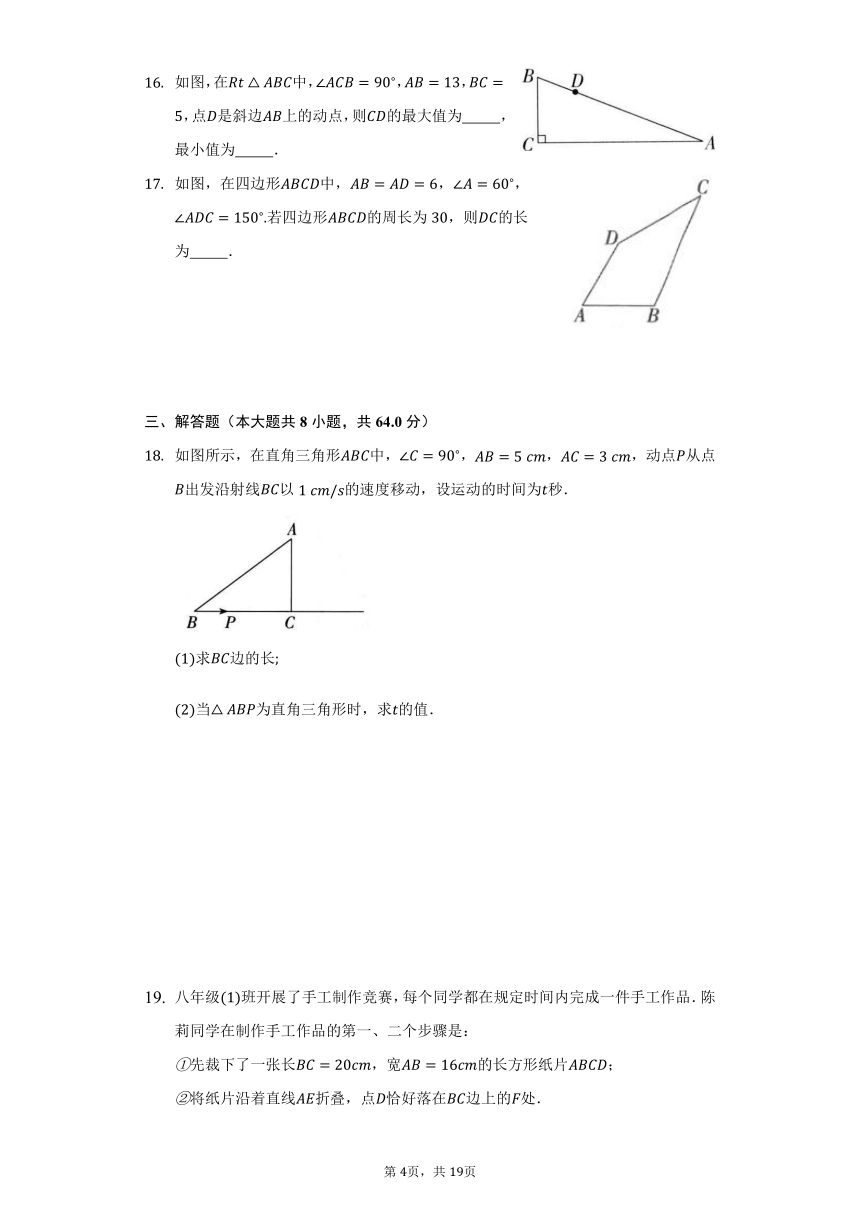
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
如图,在中,,,,高与相交于点,则的长为
A.
B.
C.
D.
将一副三角尺按如图所示的方式摆放,点在上,点在的延长线上,,,,,则的度数是
A. B. C. D.
如图所示,长方形中,点在边上,将长方形沿直线折叠,点恰好落在边上的点处,若,,则的长是
A. B. C. D.
直角三角形的三边长分别为,,,则的值有
A. 个 B. 个 C. 个 D. 个
如图,在中,,为边上的高,为边上的中线,,,则的长为
A. B. C. D.
如图,在中,平分交于点,过点作,垂足为,过点作,垂足为若,,则的度数为
A. B. C. D.
在中,,,边上的高,则另一边等于
A. B. C. 或 D. 或
如下图,数轴上点所表示的数是
A. B. C. D.
如图,已知每级台阶的宽度都是,每级台阶的高度都是,连接,则等于
A. B. C. D.
把一张宽为的长方形纸片折叠成如图所示的阴影图案,顶点,互相重合,中间空白部分是以为直角顶点,腰长为的等腰直角三角形,则纸片的长单位:为
A. B. C. D.
如果一个直角三角形的两条边长分别为和,那么这个三角形的第三边长为
A. B. C. D. 或
中,,,点是边上的动点,过点作于点,于点,则的长是
A. B. 或 C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
如图,在中,,,,垂足为,与关于所在直线对称,点的对称点是点,则的度数为 .
如图,在长方形纸片中,已知,折叠纸片使边与对角线重合,点落在点处,折痕为,且,则 .
如图,将边长为的正方形纸片折叠,使点落在边的中点处,点落在点处,折痕为,则线段的长为 .
如图,在中,,,,点是斜边上的动点,则的最大值为 ,最小值为 .
如图,在四边形中,,,若四边形的周长为,则的长为 .
三、解答题(本大题共8小题,共64.0分)
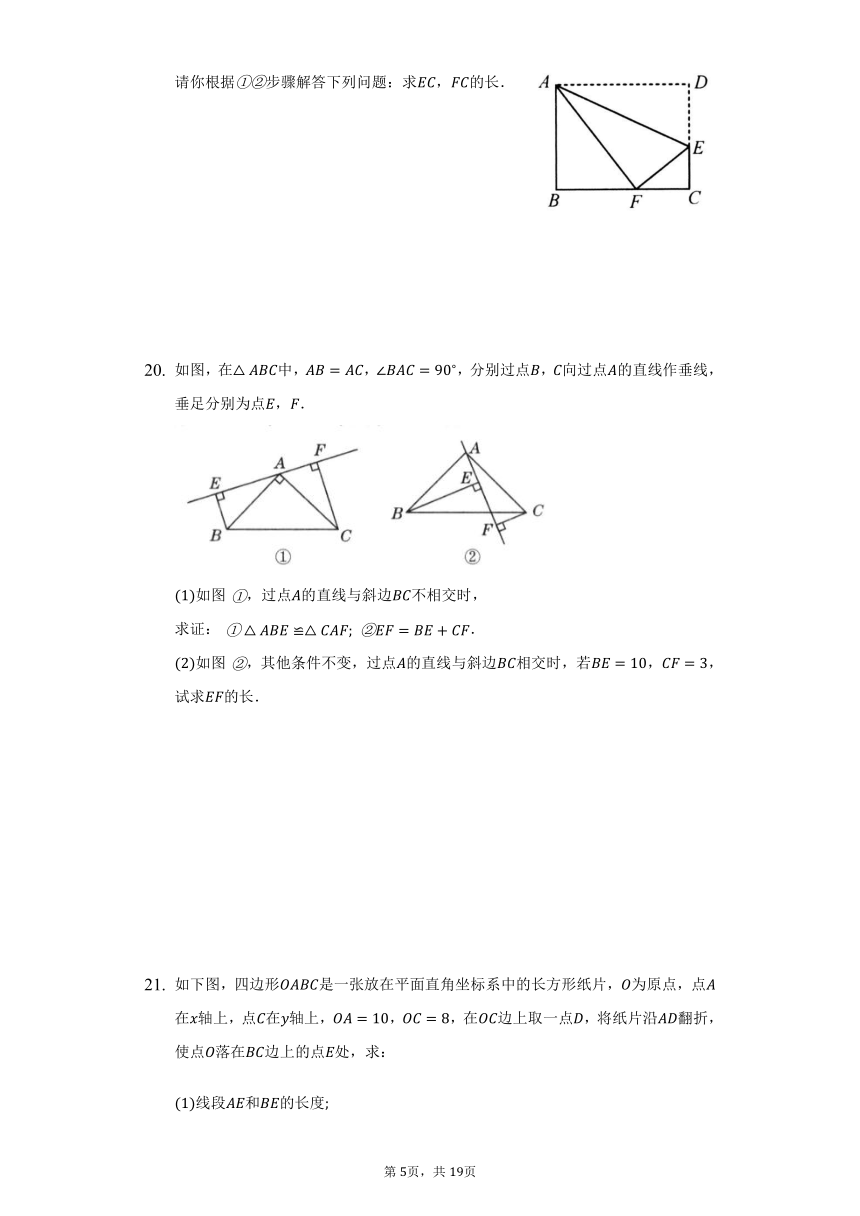
如图所示,在直角三角形中,,,,动点从点出发沿射线以的速度移动,设运动的时间为秒.
求边的长
当为直角三角形时,求的值.
八年级班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:
先裁下了一张长,宽的长方形纸片;
将纸片沿着直线折叠,点恰好落在边上的处.
请你根据步骤解答下列问题:求,的长.
如图,在中,,,分别过点,向过点的直线作垂线,垂足分别为点,.
如图,过点的直线与斜边不相交时,
求证:.
如图,其他条件不变,过点的直线与斜边相交时,若,,试求的长.
如下图,四边形是一张放在平面直角坐标系中的长方形纸片,为原点,点在轴上,点在轴上,,,在边上取一点,将纸片沿翻折,使点落在边上的点处,求:
线段和的长度
点和点的坐标.
如图,在中,,垂足为,,,.
求的长.
求的长.
如图,在四边形中,,,试说明:.
如图,在中,,,若点从点出发,以的速度沿折线向点运动,设运动时间为.
在上是否存在点,使得若存在,求出的值若不存在,请说明理由.
若点恰好在的角平分线上,请求出的值.
课间,小聪拿着老师的等腰直角三角板玩,不小心把三角板掉到两墙之间如图,,,从三角板的刻度可知,小聪很快就知道了砌墙砖块的厚度的平方每块砖的厚度相等为 .
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】,,
.
,,
.
,
,
.
故选A
3.【答案】
【解析】解:由翻折而成,
,
在中,,,
,
.
.
故选:.
4.【答案】
【解析】当为斜边长时,
当为斜边长时,,
所以的值有个.
故选:.
5.【答案】
【解析】略
6.【答案】
【解析】,,
,
平分,
,
,
,
,
,
.
7.【答案】
【解析】
【分析】
此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.
分两种情况考虑,如图所示,分别在直角三角形与直角三角形中,利用勾股定理求出与的长,即可求出的长.
【解答】
解:根据题意画出图形,如图所示,
如图所示,,,,
在和中,
根据勾股定理得:,,
此时;
如图所示,,,,
在和中,
根据勾股定理得:,,此时,
则的长为或.
故选:.
8.【答案】
【解析】解:,,
,
,
点表示的数为.
故选D.
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】解:如图,过点作于点,连结.
在中,
,,
,在中,,
,
,
,
即.
故选A.
13.【答案】
【解析】,,
.
,与关于所在直线对称,
.
,
.
14.【答案】
【解析】略
15.【答案】
【解析】解:正方形纸片的边长为,
,.
为的中点,
.
由折叠的性质,得.
设,则.
在中,
由勾股定理,得
,
即,
解得.
.
故答案为:.
16.【答案】
【解析】在中,,
,
,
为斜边上的动点,
当点运动到点时,取得最大值,
的最大值为;
根据垂线段最短可得,的最小值为斜边上的高,
由,
得,
故CD的最小值为.
17.【答案】
【解析】略
18.【答案】解:在直角三角形中,,所以.
由题意知,
如图所示,当为直角时,点与点重合,,即
如图所示,当为直角时,,,,
在直角三角形中,,
在直角三角形中,,
所以,解得.
综上,当为直角三角形时,的值为或.
【解析】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
直接根据勾股定理求出的长度;
当为直角三角形时,分两种情况:当为直角时,当为直角时,分别求出此时的值即可.
19.【答案】解:因为与关于对称,
所以≌.
所以,.
因为,,
所以,.
在中,由勾股定理,得.
,
.
所以.
设,则,
在中,由勾股定理,得,
解得.
所以.
【解析】见答案
20.【答案】证明:,,
.
.
,.
.
在和中,
.
由知,
,.
.
解:,,
.
.
,
.
.
在和中,
.
,.
.
【解析】见答案
21.【答案】依题意可知,折痕是四边形的对称轴,
在中,,,
.
,,.
在中,.
又,,
,.
综上,点坐标为,点坐标为.
【解析】略
22.【答案】解:因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
所以.
【解析】见答案.
23.【答案】解:连接,
因为,
所以.
所以.
又因为,
所以.
所以 ,即.
所以.
【解析】见答案
24.【答案】解:存在
,,,
由勾股定理,得.
假设存在点,使得,则,.
在中,由勾股定理,得,
即,
解得.
存在满足条件的点,此时的值为
当点在点或点处时,一定在的角平分线上,此时或.
如图,当点在边上,且点在的平分线上时,.
过点作,垂足为,易得.
,.
.
在中,由,
得,解得.
如图,当点在边上,且点在的平分线上时,
,.
过点作,垂足为,易得 .
,.
在中,由 ,
得,解得.
综上所述,当点恰好在的角平分线上时,的值为或或或.
【解析】见答案.
25.【答案】
【解析】略
第2页,共2页
第1页,共1页
18.1 勾股定理同步练习
沪科版版初中数学八年级下册
学校:___________姓名:___________班级:___________考号:___________
注意:本试卷包含Ⅰ、Ⅱ两卷。第Ⅰ卷为选择题,所有答案必须用2B铅笔涂在答题卡中相应的位置。第Ⅱ卷为非选择题,所有答案必须填在答题卷的相应位置。答案写在试卷上均无效,不予记分。
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分)
如图,在中,,,,高与相交于点,则的长为
A.
B.
C.
D.
将一副三角尺按如图所示的方式摆放,点在上,点在的延长线上,,,,,则的度数是
A. B. C. D.
如图所示,长方形中,点在边上,将长方形沿直线折叠,点恰好落在边上的点处,若,,则的长是
A. B. C. D.
直角三角形的三边长分别为,,,则的值有
A. 个 B. 个 C. 个 D. 个
如图,在中,,为边上的高,为边上的中线,,,则的长为
A. B. C. D.
如图,在中,平分交于点,过点作,垂足为,过点作,垂足为若,,则的度数为
A. B. C. D.
在中,,,边上的高,则另一边等于
A. B. C. 或 D. 或
如下图,数轴上点所表示的数是
A. B. C. D.
如图,已知每级台阶的宽度都是,每级台阶的高度都是,连接,则等于
A. B. C. D.
把一张宽为的长方形纸片折叠成如图所示的阴影图案,顶点,互相重合,中间空白部分是以为直角顶点,腰长为的等腰直角三角形,则纸片的长单位:为
A. B. C. D.
如果一个直角三角形的两条边长分别为和,那么这个三角形的第三边长为
A. B. C. D. 或
中,,,点是边上的动点,过点作于点,于点,则的长是
A. B. 或 C. D.
第II卷(非选择题)
二、填空题(本大题共5小题,共15.0分)
如图,在中,,,,垂足为,与关于所在直线对称,点的对称点是点,则的度数为 .
如图,在长方形纸片中,已知,折叠纸片使边与对角线重合,点落在点处,折痕为,且,则 .
如图,将边长为的正方形纸片折叠,使点落在边的中点处,点落在点处,折痕为,则线段的长为 .
如图,在中,,,,点是斜边上的动点,则的最大值为 ,最小值为 .
如图,在四边形中,,,若四边形的周长为,则的长为 .
三、解答题(本大题共8小题,共64.0分)
如图所示,在直角三角形中,,,,动点从点出发沿射线以的速度移动,设运动的时间为秒.
求边的长
当为直角三角形时,求的值.
八年级班开展了手工制作竞赛,每个同学都在规定时间内完成一件手工作品.陈莉同学在制作手工作品的第一、二个步骤是:
先裁下了一张长,宽的长方形纸片;
将纸片沿着直线折叠,点恰好落在边上的处.
请你根据步骤解答下列问题:求,的长.
如图,在中,,,分别过点,向过点的直线作垂线,垂足分别为点,.
如图,过点的直线与斜边不相交时,
求证:.
如图,其他条件不变,过点的直线与斜边相交时,若,,试求的长.
如下图,四边形是一张放在平面直角坐标系中的长方形纸片,为原点,点在轴上,点在轴上,,,在边上取一点,将纸片沿翻折,使点落在边上的点处,求:
线段和的长度
点和点的坐标.
如图,在中,,垂足为,,,.
求的长.
求的长.
如图,在四边形中,,,试说明:.
如图,在中,,,若点从点出发,以的速度沿折线向点运动,设运动时间为.
在上是否存在点,使得若存在,求出的值若不存在,请说明理由.
若点恰好在的角平分线上,请求出的值.
课间,小聪拿着老师的等腰直角三角板玩,不小心把三角板掉到两墙之间如图,,,从三角板的刻度可知,小聪很快就知道了砌墙砖块的厚度的平方每块砖的厚度相等为 .
答案和解析
1.【答案】
【解析】略
2.【答案】
【解析】,,
.
,,
.
,
,
.
故选A
3.【答案】
【解析】解:由翻折而成,
,
在中,,,
,
.
.
故选:.
4.【答案】
【解析】当为斜边长时,
当为斜边长时,,
所以的值有个.
故选:.
5.【答案】
【解析】略
6.【答案】
【解析】,,
,
平分,
,
,
,
,
,
.
7.【答案】
【解析】
【分析】
此题考查了勾股定理,熟练掌握勾股定理是解本题的关键.
分两种情况考虑,如图所示,分别在直角三角形与直角三角形中,利用勾股定理求出与的长,即可求出的长.
【解答】
解:根据题意画出图形,如图所示,
如图所示,,,,
在和中,
根据勾股定理得:,,
此时;
如图所示,,,,
在和中,
根据勾股定理得:,,此时,
则的长为或.
故选:.
8.【答案】
【解析】解:,,
,
,
点表示的数为.
故选D.
9.【答案】
【解析】略
10.【答案】
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】解:如图,过点作于点,连结.
在中,
,,
,在中,,
,
,
,
即.
故选A.
13.【答案】
【解析】,,
.
,与关于所在直线对称,
.
,
.
14.【答案】
【解析】略
15.【答案】
【解析】解:正方形纸片的边长为,
,.
为的中点,
.
由折叠的性质,得.
设,则.
在中,
由勾股定理,得
,
即,
解得.
.
故答案为:.
16.【答案】
【解析】在中,,
,
,
为斜边上的动点,
当点运动到点时,取得最大值,
的最大值为;
根据垂线段最短可得,的最小值为斜边上的高,
由,
得,
故CD的最小值为.
17.【答案】
【解析】略
18.【答案】解:在直角三角形中,,所以.
由题意知,
如图所示,当为直角时,点与点重合,,即
如图所示,当为直角时,,,,
在直角三角形中,,
在直角三角形中,,
所以,解得.
综上,当为直角三角形时,的值为或.
【解析】本题考查了勾股定理,解答本题的关键是掌握勾股定理的应用,以及分情况讨论,注意不要漏解.
直接根据勾股定理求出的长度;
当为直角三角形时,分两种情况:当为直角时,当为直角时,分别求出此时的值即可.
19.【答案】解:因为与关于对称,
所以≌.
所以,.
因为,,
所以,.
在中,由勾股定理,得.
,
.
所以.
设,则,
在中,由勾股定理,得,
解得.
所以.
【解析】见答案
20.【答案】证明:,,
.
.
,.
.
在和中,
.
由知,
,.
.
解:,,
.
.
,
.
.
在和中,
.
,.
.
【解析】见答案
21.【答案】依题意可知,折痕是四边形的对称轴,
在中,,,
.
,,.
在中,.
又,,
,.
综上,点坐标为,点坐标为.
【解析】略
22.【答案】解:因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
在中,
因为,
所以.
所以.
因为,
所以.
所以.
【解析】见答案.
23.【答案】解:连接,
因为,
所以.
所以.
又因为,
所以.
所以 ,即.
所以.
【解析】见答案
24.【答案】解:存在
,,,
由勾股定理,得.
假设存在点,使得,则,.
在中,由勾股定理,得,
即,
解得.
存在满足条件的点,此时的值为
当点在点或点处时,一定在的角平分线上,此时或.
如图,当点在边上,且点在的平分线上时,.
过点作,垂足为,易得.
,.
.
在中,由,
得,解得.
如图,当点在边上,且点在的平分线上时,
,.
过点作,垂足为,易得 .
,.
在中,由 ,
得,解得.
综上所述,当点恰好在的角平分线上时,的值为或或或.
【解析】见答案.
25.【答案】
【解析】略
第2页,共2页
第1页,共1页
