2021-2022学年北师大版九年级数学下册 3.2圆的对称性 解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册 3.2圆的对称性 解答题专题提升训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 401.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 19:52:56 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3-2圆的对称性》解答题专题提升训练(附答案)
1.如图,AB是⊙O的弦,点C、D是的三等分点,半径OC、OD分别与弦AB交于点E、F,连接OA、OB、AC、BD.
(1)求证:AE=BF;
(2)在不添加任何辅助线的情况下,直接写出图中所有的全等三角形.
2.如图,点A、B、C、D在⊙O上,AB=CD.求证:AC=BD.
3.如图,以平行四边形ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC、AD于E、F两点,交BA的延长线于点G.
(1)求证:=;
(2)若为140°,求∠EGB的度数.
4.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求BE、CF的长.
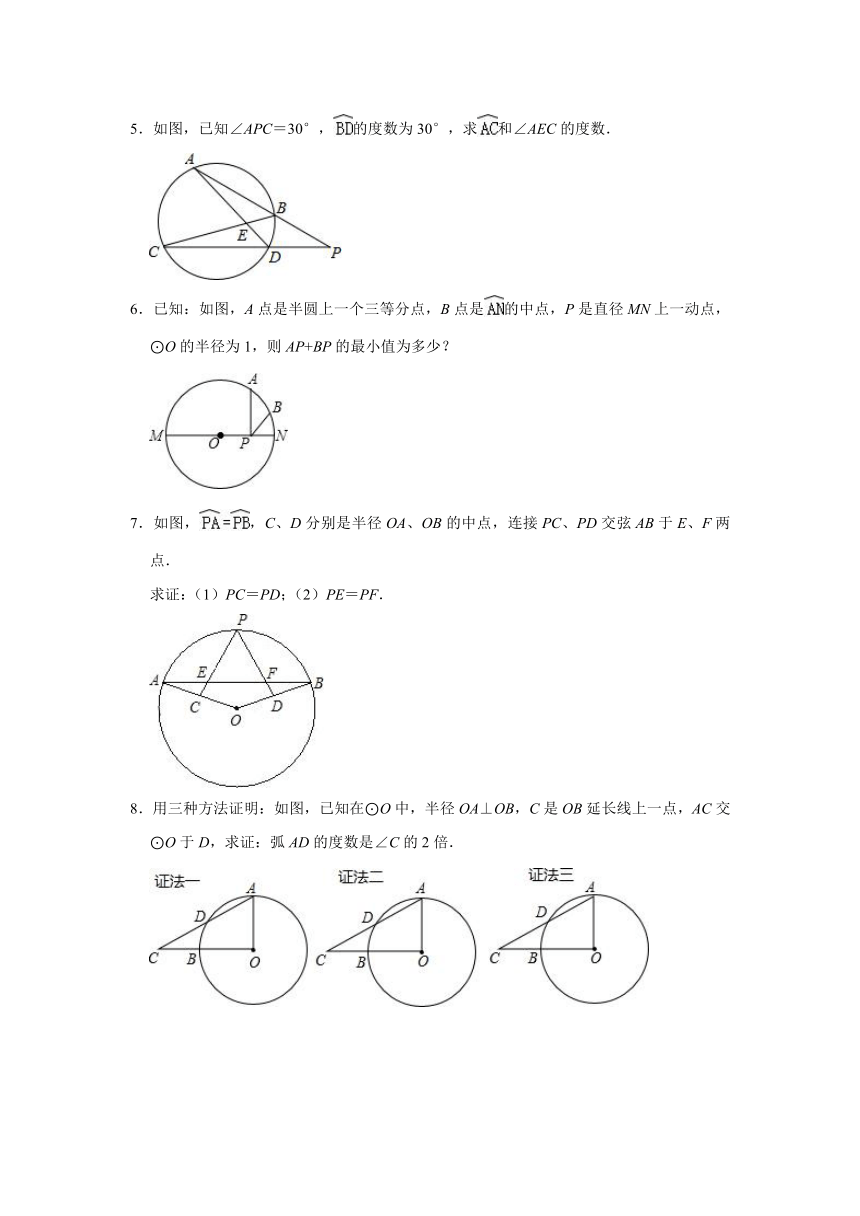
5.如图,已知∠APC=30°,的度数为30°,求和∠AEC的度数.
6.已知:如图,A点是半圆上一个三等分点,B点是的中点,P是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为多少?
7.如图,,C、D分别是半径OA、OB的中点,连接PC、PD交弦AB于E、F两点.
求证:(1)PC=PD;(2)PE=PF.
8.用三种方法证明:如图,已知在⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于D,求证:弧AD的度数是∠C的2倍.
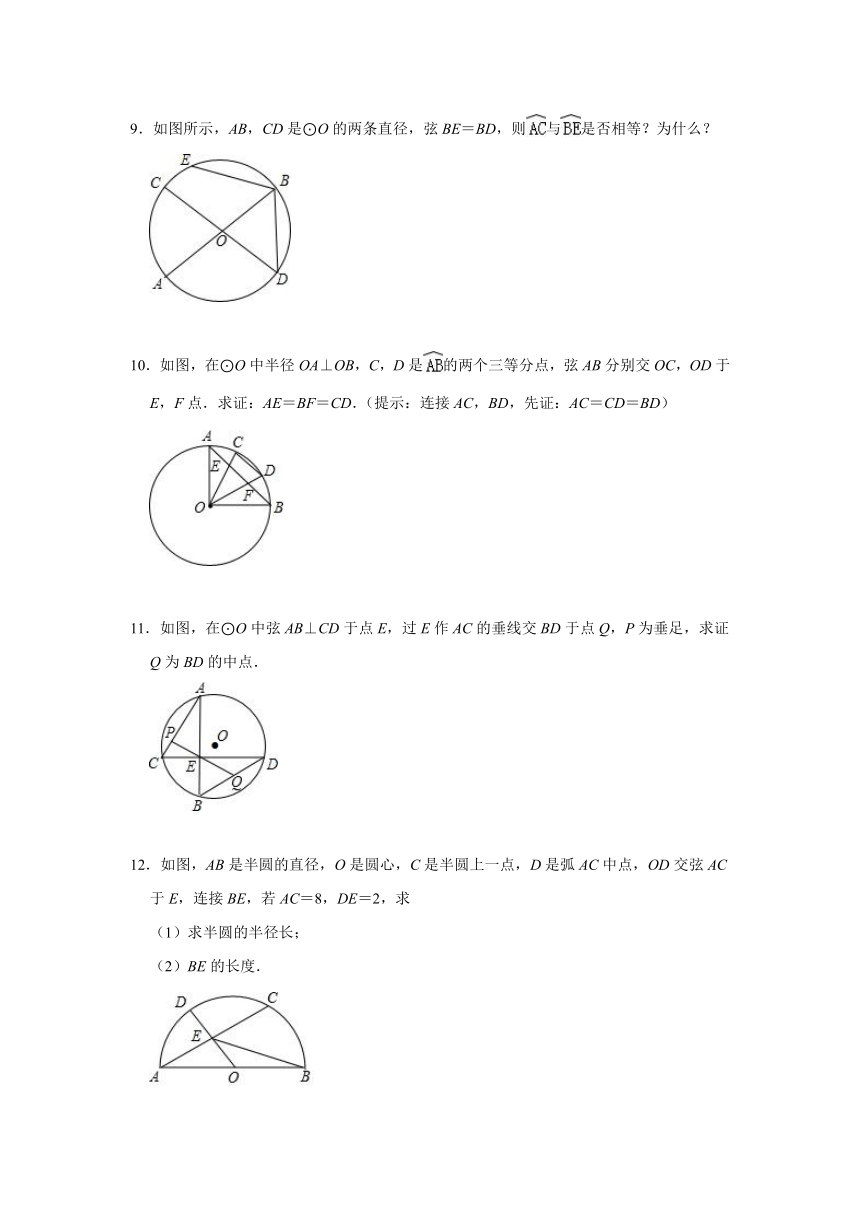
9.如图所示,AB,CD是⊙O的两条直径,弦BE=BD,则与是否相等?为什么?
10.如图,在⊙O中半径OA⊥OB,C,D是的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.(提示:连接AC,BD,先证:AC=CD=BD)
11.如图,在⊙O中弦AB⊥CD于点E,过E作AC的垂线交BD于点Q,P为垂足,求证Q为BD的中点.
12.如图,AB是半圆的直径,O是圆心,C是半圆上一点,D是弧AC中点,OD交弦AC于E,连接BE,若AC=8,DE=2,求
(1)求半圆的半径长;
(2)BE的长度.
13.已知如图所示,P为直径AB上一点,EF,CD为过点P的两条弦,且∠DPB=∠EPB;
(1)求证:;
(2)求证:CE=DF.
14.如图,已知CE是⊙O的直径,弦AB与CD交点P,且AC=CP,点B关于CE的对称点是点F,点G是上的一点,连接AD,GD,若==.
(1)求证:=;
(2)若AC=2,DP=3,求弦GD的长.
15.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知=.
(1)求证:BE=DE;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AE的长.
16.如图,弦AB=CD,AB与CD相交于点E,求证:(1)=;(2)AE=DE.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
(1)求证:点E是的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.
18.如图所示,M、N分别是⊙O的弦AB、CD的中点,AB=CD.求证:∠AMN=∠CNM.
19.如图,点A、B、C是⊙O上的三点,AB∥OC.
(1)求证:AC平分∠OAB.
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求OE的长.
20.小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.
(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,PA,PB组成⊙O的一条折弦.C是劣弧AB的中点,直线CD⊥PA于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;
(3)如图3,PA.PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.
参考答案
1.证明:(1)∵点C、D是的三等分点,
∴∠AOC=∠BOD,
∵OA、OB是⊙O的半径,
∴OA=OB,
∴∠OAE=∠OBF,
∴△OAE≌△OBF,
∴AE=BF;
(2)图中所有的全等三角形为:△OAE≌△OBF,△OAC≌△OBD,△AEC≌△BFD,△OAF≌△OBE.
2.证明:∵AB=CD,
∴,
∴,即,
∴AC=BD.
3.(1)证明:连接AE.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,∠GAF=∠B,
∵AE=AB,
∴∠B=∠AEB,
∴∠EAF=∠GAF,
∴=;
(2)∵GB为⊙A的直径,
∴为180°,
∵为140°,
∴为40°,
∴∠BAE=40°
∵∠EGB=∠BAE,
∴∠EGB=20°.
4.(1)证明:延长CE交⊙O于点P,
∵CE⊥AB,
∴=,
∴∠BCP=∠BDC,
∵C是的中点,
∴CD=CB,
∴∠BDC=∠CBD,
∴∠CBD=∠BCP,
∴CF=BF;
(2)∵CD=6,AC=8,
∴AB=10,
∴BE==3.6,
∴CE==4.8,设CF=x,则FE=4.8﹣x,BF=x,
∴(4.8﹣x)2+3.62=x2,
∴x=.
5.解:连接AC,
∵=30°,
∴∠1=∠2==15°,
∵∠APC=30°,∠ADC是△APD的外角,
∴∠ADC=∠1+∠APC=15°+30°=45°,
∴=2∠ADC=90°;
∵∠AEC是△CDE的外角,
∴∠AEC=∠ADC+∠2=45°+15°=60°.
故答案为:90°,60°.
6.解:作A关于MN的对称点A′,根据圆的对称性,则A′必在圆上,
连接BA′交MN于P,连接PA,则PA+PB最小,此时PA+PB=PA′+PB=A′B,
连接OA、OA′、OB,
∵,
∴∠AON=∠A′ON=60°.
∵,
∴∠BON=∠AON=30°.
∴∠A′OB=90°.
∴A′B==.
即AP+BP的最小值是.
7.证明:(1)连接PO,
∵=,
∴∠POC=∠POD.
∵C、D分别是半径OA、OB的中点,
∴OC=OD.
∵PO=PO,
∴△PCO≌△PDO.
∴PC=PD.
(2)∵△PCO≌△PDO,
∴∠PCO=∠PDO.
∵OA=OB,
∴∠A=∠B.
∴∠AEC=∠BFD.
∴∠PEF=∠PFE.
∴PE=PF.
8.证明:
证法一:延长AO交圆与点M,连接DM,
∵AM是圆的直径,
∵∠ADM=90°则△OAC与△ADM都是直角三角形,且∠A是公共角,
∴∠M=∠C,而∠AOD=2∠M.
∴∠AOD=2∠C.
∵∠AOD的度数就等于弧AD的度数,
∴弧AD的度数是∠C的2倍.
证法二:连接OD,
在直角△AOC中,∠C=90°﹣∠A,
在△OAD中,∵OA=OD,
∴∠A=∠ADO.
∴∠AOD=180﹣2∠A.
∴∠AOD=2∠C.
∵∠AOD的度数就等于弧AD的度数,
∴弧AD的度数是∠C的2倍.
证法三:延长AO交圆于点N,连接CN,交圆于点M,连接OM、OD,
∵AN⊥OC,OA=ON,
∴AC=CN.
∴∠A=∠N,∠ACN=2∠ACO.
∴∠ACN=180﹣∠A﹣∠N=180﹣2∠A.
∵△OAD中OA=OD,
∴∠A=∠ADO=∠N.
∴∠AOD=∠ACN=2∠ACO.
又∵∠AOD的度数就等于弧AD的度数,
弧AD的度数是∠ACO的2倍.
9.解:与相等,理由为:
∵AB,CD为圆的直径,
∴∠AOC=∠BOD,
∴=,
∵BE=BD,
∴=,
则=.
10.解:连接AC、BD,
∵C,D是的三等分点,
∴AC=CD=BD,∠AOC=∠COD,OA=OC=OD,
在△ACO与△DCO中,
∵
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC,
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD,
∴AE=BF=CD.
11.证明:∵AB⊥CD于点E,过E作AC的垂线交BD于点Q,
∴三角形ACE、三角形PCE、三角形APE、三角形BED都是直角三角形.
∴∠DEQ=∠CEP(对顶角相等).
∠CEP=∠A(同角的余角相等).
又∵∠A=∠D(同弧所对的圆周角相等),
∴∠DEQ=∠D,∴EQ=QD(等角对等边).
又∵∠QEB=∠B(等角的余角相等),
∴EQ=QB.
∴EQ=QD=QB,即Q为BD的中点.
12.解:(1)设圆的半径为r,
∵D是弧AC中点,
∴OD⊥AC,AE=AC=4,
在Rt△AOE中,OA2=OE2+AE2,即r2=(r﹣2)2+42,
解得,r=5,即圆的半径长为5;
(2)连接BC,
∵AO=OB,AE=EC,
∴BC=2OE=6,
∵AB是半圆的直径,
∴∠ACB=90°,
∴BE==2.
13.证明:(1)作ON⊥EF,OM⊥CD,
∵∠DPB=∠EPB;
∴ON=OM,
∴CD=EF,
∴=,﹣=﹣,
即.
(2)证明:∵
∴CE=DF.
14.(1)证明:∵点B关于CE的对称点是点F,
∴EC⊥BF,
∴=,
∵=,
∴=,
∴=.
(2)连接BC、BE、BD,作CH⊥AB于H.
∵CA=CP,
∴∠CAP=∠CPA,∠CPA=∠BPD,
∵∠CAP=∠BDP,
∴∠BPD=∠BDP,
∴BP=BD,
∵=,
∴∠ABD=∠CDB,
∴PB=PD,
∴PB=PD=BD,
∴△PDB是等边三角形,
∴∠BDP=∠BPD=∠APC=60°,
∴△ACP是等边三角形,
∵AC=2,PD=3,CH⊥AP,
∴AH=PH=2,BH=PB+PH=3,CH=,
∴BC==,
∵∠CEB=∠CDB=60°,EC是直径,
∴∠CBE=90°,
∴BE=BC tan30°=,
∵EC⊥BF,
∴=,
∵=,
∴=,
∴=,
∴DG=BE=.
15.解:(1)∵=,
∴AB=CD,
在△ABE与△CDE中,,
∴△ABE≌△CDE,
∴BE=DE;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
根据垂径定理得:AF=FD,BG=OG,
∵AD=BC,
∴AF=CG,
在Rt△AOF与Rt△OCG中,
,
∴Rt△AOF≌Rt△OCG(HL),
∴OF=OG,
∵AD⊥CB,
∴四边形OFEG是正方形,
∴OF=EF,
设OF=EF=x,
则AF=FD=x+1,
∴OF2+AF2=OA2,
即:x2+(x+1)2=52,
解得:x=3,x=﹣4(舍去),
∴AF=4,
∴AE=7.
16.证明(1)∵弦AB=CD,
∴=,
∴﹣=﹣,
即=;
(2)∵=,
∴∠A=∠D,
∴AE=DE.
17.(1)证明:连接AE,DE
∵AB是直径,
∴AE⊥BC,
∵AB=AC,
∴BE=EC,
∵∠CDB=90°,DE是斜边BC的中线,
∴DE=EB,
∴,
即点E是的中点;
(2)设AD=x,则CD=2x,
∴AB=AC=3x,
∵AB为直径,
∴∠ADB=90°,
∴BD2=(3x)2﹣x2=8x2,
在Rt△CDB中,
(2x)2+8x2=122,
∴,
∴,
即⊙O的半径是3.
18.证明:连接OM、ON,
∵O为圆心,M、N分别为弦AB、CD的中点,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.
∴∠OMN=∠ONM.
∵∠AMN=90°﹣∠OMN,
∵∠CNM=90°﹣∠ONM,
∴∠AMN=∠CNM.
19.(1)证明:∵AB∥OC,
∴∠C=∠BAC.
∵OA=OC,
∴∠C=∠OAC.
∴∠BAC=∠OAC.
即AC平分∠OAB.
(2)解:∵OE⊥AB,
∴AE=BE=AB=1.
又∵∠AOE=30°,∠PEA=90°,
∴∠OAE=60°.
∴OE=AB cos60°=2×=.
20.证明:(1)如图1,连接AD,BD,
∵C是劣弧AB的中点,
∴∠CDA=∠CDB,
∵DE⊥AB,
∴∠AED=∠DEB=90°,
∴∠A+∠ADE=90°,∠B+∠CDB=90°,
∴∠A=∠B,
∴△ADB为等腰三角形,
∵CD⊥AB,
∴AE=BE;
(2)如图2,延长DB、AP相交于点F,再连接AD,
∵ADBP是圆内接四边形,
∴∠PBF=∠PAD,
∵C是劣弧AB的中点,
∴∠CDA=∠CDF,
∵CD⊥PA,
∴△AFD为等腰三角形,
∴∠F=∠A,AE=EF,
∴∠PBF=∠F,
∴PB=PF,
∴AE=PE+PB
(3)AE=PE﹣PB.
连接AD,BD,AB,DB、AP相交于点F,
∵弧AC=弧BC,
∴∠ADC=∠BDC,
∵CD⊥AP,
∴∠DEA=∠DEF,∠ADE=∠FDE,
∵DE=DE,
∴△DAE≌△DFE,
∴AD=DF,AE=EF,
∴∠DAF=∠DFA,
∴∠DFA=∠PFB,∠PBD=∠DAP,
∴∠PFB=∠PBF,
∴PF=PB,
∴AE=PE﹣PB.
1.如图,AB是⊙O的弦,点C、D是的三等分点,半径OC、OD分别与弦AB交于点E、F,连接OA、OB、AC、BD.
(1)求证:AE=BF;
(2)在不添加任何辅助线的情况下,直接写出图中所有的全等三角形.
2.如图,点A、B、C、D在⊙O上,AB=CD.求证:AC=BD.
3.如图,以平行四边形ABCD的顶点A为圆心,AB为半径作⊙A,分别交BC、AD于E、F两点,交BA的延长线于点G.
(1)求证:=;
(2)若为140°,求∠EGB的度数.
4.如图,AB是⊙O的直径,C是的中点,CE⊥AB于E,BD交CE于F.
(1)求证:CF=BF;
(2)若CD=6,AC=8,求BE、CF的长.
5.如图,已知∠APC=30°,的度数为30°,求和∠AEC的度数.
6.已知:如图,A点是半圆上一个三等分点,B点是的中点,P是直径MN上一动点,⊙O的半径为1,则AP+BP的最小值为多少?
7.如图,,C、D分别是半径OA、OB的中点,连接PC、PD交弦AB于E、F两点.
求证:(1)PC=PD;(2)PE=PF.
8.用三种方法证明:如图,已知在⊙O中,半径OA⊥OB,C是OB延长线上一点,AC交⊙O于D,求证:弧AD的度数是∠C的2倍.
9.如图所示,AB,CD是⊙O的两条直径,弦BE=BD,则与是否相等?为什么?
10.如图,在⊙O中半径OA⊥OB,C,D是的两个三等分点,弦AB分别交OC,OD于E,F点.求证:AE=BF=CD.(提示:连接AC,BD,先证:AC=CD=BD)
11.如图,在⊙O中弦AB⊥CD于点E,过E作AC的垂线交BD于点Q,P为垂足,求证Q为BD的中点.
12.如图,AB是半圆的直径,O是圆心,C是半圆上一点,D是弧AC中点,OD交弦AC于E,连接BE,若AC=8,DE=2,求
(1)求半圆的半径长;
(2)BE的长度.
13.已知如图所示,P为直径AB上一点,EF,CD为过点P的两条弦,且∠DPB=∠EPB;
(1)求证:;
(2)求证:CE=DF.
14.如图,已知CE是⊙O的直径,弦AB与CD交点P,且AC=CP,点B关于CE的对称点是点F,点G是上的一点,连接AD,GD,若==.
(1)求证:=;
(2)若AC=2,DP=3,求弦GD的长.
15.如图,在⊙O中,弦AD、BC相交于点E,连接OE,已知=.
(1)求证:BE=DE;
(2)如果⊙O的半径为5,AD⊥CB,DE=1,求AE的长.
16.如图,弦AB=CD,AB与CD相交于点E,求证:(1)=;(2)AE=DE.
17.如图,在△ABC中,AB=AC,以AB为直径的半圆分别交AC,BC边于点D,E,连接BD,
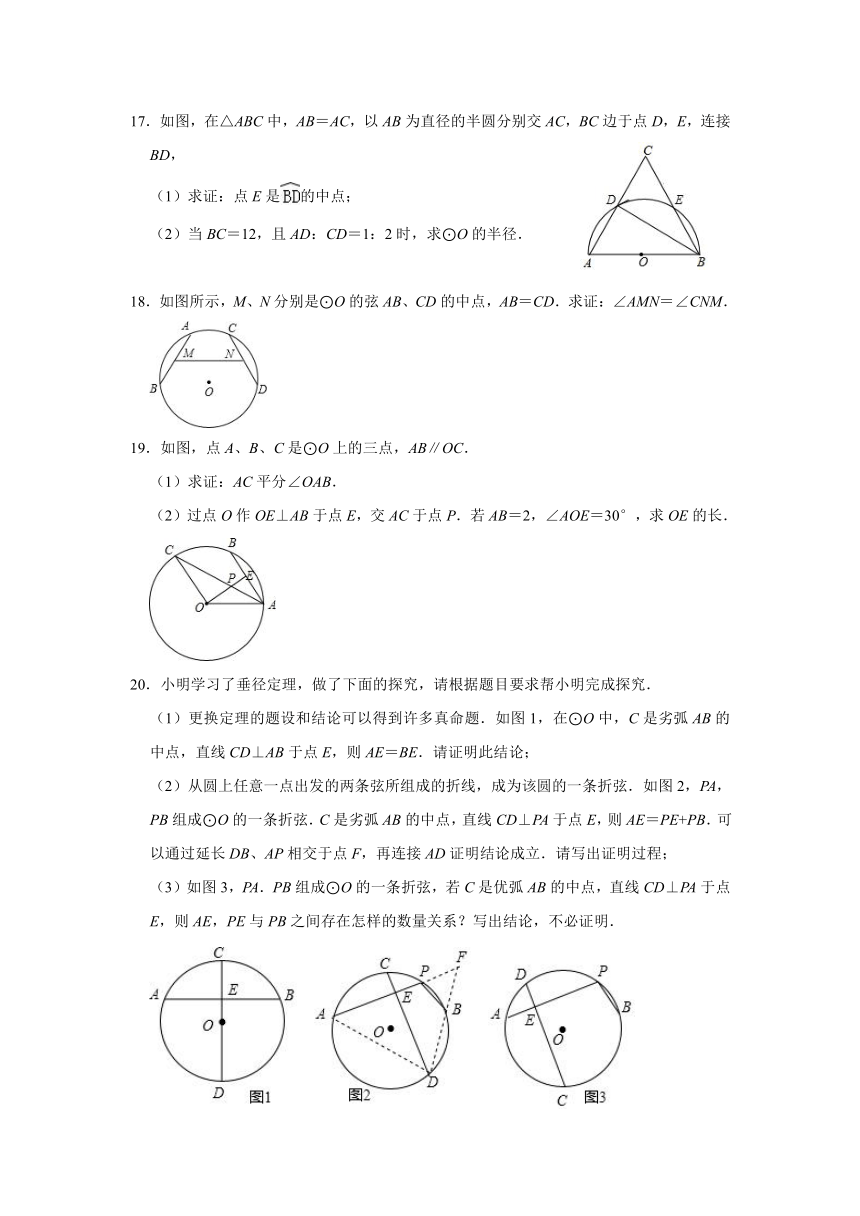
(1)求证:点E是的中点;
(2)当BC=12,且AD:CD=1:2时,求⊙O的半径.
18.如图所示,M、N分别是⊙O的弦AB、CD的中点,AB=CD.求证:∠AMN=∠CNM.
19.如图,点A、B、C是⊙O上的三点,AB∥OC.
(1)求证:AC平分∠OAB.
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求OE的长.
20.小明学习了垂径定理,做了下面的探究,请根据题目要求帮小明完成探究.
(1)更换定理的题设和结论可以得到许多真命题.如图1,在⊙O中,C是劣弧AB的中点,直线CD⊥AB于点E,则AE=BE.请证明此结论;
(2)从圆上任意一点出发的两条弦所组成的折线,成为该圆的一条折弦.如图2,PA,PB组成⊙O的一条折弦.C是劣弧AB的中点,直线CD⊥PA于点E,则AE=PE+PB.可以通过延长DB、AP相交于点F,再连接AD证明结论成立.请写出证明过程;
(3)如图3,PA.PB组成⊙O的一条折弦,若C是优弧AB的中点,直线CD⊥PA于点E,则AE,PE与PB之间存在怎样的数量关系?写出结论,不必证明.
参考答案
1.证明:(1)∵点C、D是的三等分点,
∴∠AOC=∠BOD,
∵OA、OB是⊙O的半径,
∴OA=OB,
∴∠OAE=∠OBF,
∴△OAE≌△OBF,
∴AE=BF;
(2)图中所有的全等三角形为:△OAE≌△OBF,△OAC≌△OBD,△AEC≌△BFD,△OAF≌△OBE.
2.证明:∵AB=CD,
∴,
∴,即,
∴AC=BD.
3.(1)证明:连接AE.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠EAF=∠AEB,∠GAF=∠B,
∵AE=AB,
∴∠B=∠AEB,
∴∠EAF=∠GAF,
∴=;
(2)∵GB为⊙A的直径,
∴为180°,
∵为140°,
∴为40°,
∴∠BAE=40°
∵∠EGB=∠BAE,
∴∠EGB=20°.
4.(1)证明:延长CE交⊙O于点P,
∵CE⊥AB,
∴=,
∴∠BCP=∠BDC,
∵C是的中点,
∴CD=CB,
∴∠BDC=∠CBD,
∴∠CBD=∠BCP,
∴CF=BF;
(2)∵CD=6,AC=8,
∴AB=10,
∴BE==3.6,
∴CE==4.8,设CF=x,则FE=4.8﹣x,BF=x,
∴(4.8﹣x)2+3.62=x2,
∴x=.
5.解:连接AC,
∵=30°,
∴∠1=∠2==15°,
∵∠APC=30°,∠ADC是△APD的外角,
∴∠ADC=∠1+∠APC=15°+30°=45°,
∴=2∠ADC=90°;
∵∠AEC是△CDE的外角,
∴∠AEC=∠ADC+∠2=45°+15°=60°.
故答案为:90°,60°.
6.解:作A关于MN的对称点A′,根据圆的对称性,则A′必在圆上,
连接BA′交MN于P,连接PA,则PA+PB最小,此时PA+PB=PA′+PB=A′B,
连接OA、OA′、OB,
∵,
∴∠AON=∠A′ON=60°.
∵,
∴∠BON=∠AON=30°.
∴∠A′OB=90°.
∴A′B==.
即AP+BP的最小值是.
7.证明:(1)连接PO,
∵=,
∴∠POC=∠POD.
∵C、D分别是半径OA、OB的中点,
∴OC=OD.
∵PO=PO,
∴△PCO≌△PDO.
∴PC=PD.
(2)∵△PCO≌△PDO,
∴∠PCO=∠PDO.
∵OA=OB,
∴∠A=∠B.
∴∠AEC=∠BFD.
∴∠PEF=∠PFE.
∴PE=PF.
8.证明:
证法一:延长AO交圆与点M,连接DM,
∵AM是圆的直径,
∵∠ADM=90°则△OAC与△ADM都是直角三角形,且∠A是公共角,
∴∠M=∠C,而∠AOD=2∠M.
∴∠AOD=2∠C.
∵∠AOD的度数就等于弧AD的度数,
∴弧AD的度数是∠C的2倍.
证法二:连接OD,
在直角△AOC中,∠C=90°﹣∠A,
在△OAD中,∵OA=OD,
∴∠A=∠ADO.
∴∠AOD=180﹣2∠A.
∴∠AOD=2∠C.
∵∠AOD的度数就等于弧AD的度数,
∴弧AD的度数是∠C的2倍.
证法三:延长AO交圆于点N,连接CN,交圆于点M,连接OM、OD,
∵AN⊥OC,OA=ON,
∴AC=CN.
∴∠A=∠N,∠ACN=2∠ACO.
∴∠ACN=180﹣∠A﹣∠N=180﹣2∠A.
∵△OAD中OA=OD,
∴∠A=∠ADO=∠N.
∴∠AOD=∠ACN=2∠ACO.
又∵∠AOD的度数就等于弧AD的度数,
弧AD的度数是∠ACO的2倍.
9.解:与相等,理由为:
∵AB,CD为圆的直径,
∴∠AOC=∠BOD,
∴=,
∵BE=BD,
∴=,
则=.
10.解:连接AC、BD,
∵C,D是的三等分点,
∴AC=CD=BD,∠AOC=∠COD,OA=OC=OD,
在△ACO与△DCO中,
∵
∴△ACO≌△DCO(SAS),
∴∠ACO=∠OCD.
∵∠OEF=∠OAE+∠AOE=45°+30°=75°,∠OCD==75°,
∴∠OEF=∠OCD,
∴CD∥AB,
∴∠AEC=∠OCD,
∴∠ACO=∠AEC,
∴AC=AE,
同理,BF=BD.
又∵AC=CD=BD,
∴AE=BF=CD.
11.证明:∵AB⊥CD于点E,过E作AC的垂线交BD于点Q,
∴三角形ACE、三角形PCE、三角形APE、三角形BED都是直角三角形.
∴∠DEQ=∠CEP(对顶角相等).
∠CEP=∠A(同角的余角相等).
又∵∠A=∠D(同弧所对的圆周角相等),
∴∠DEQ=∠D,∴EQ=QD(等角对等边).
又∵∠QEB=∠B(等角的余角相等),
∴EQ=QB.
∴EQ=QD=QB,即Q为BD的中点.
12.解:(1)设圆的半径为r,
∵D是弧AC中点,
∴OD⊥AC,AE=AC=4,
在Rt△AOE中,OA2=OE2+AE2,即r2=(r﹣2)2+42,
解得,r=5,即圆的半径长为5;
(2)连接BC,
∵AO=OB,AE=EC,
∴BC=2OE=6,
∵AB是半圆的直径,
∴∠ACB=90°,
∴BE==2.
13.证明:(1)作ON⊥EF,OM⊥CD,
∵∠DPB=∠EPB;
∴ON=OM,
∴CD=EF,
∴=,﹣=﹣,
即.
(2)证明:∵
∴CE=DF.
14.(1)证明:∵点B关于CE的对称点是点F,
∴EC⊥BF,
∴=,
∵=,
∴=,
∴=.
(2)连接BC、BE、BD,作CH⊥AB于H.
∵CA=CP,
∴∠CAP=∠CPA,∠CPA=∠BPD,
∵∠CAP=∠BDP,
∴∠BPD=∠BDP,
∴BP=BD,
∵=,
∴∠ABD=∠CDB,
∴PB=PD,
∴PB=PD=BD,
∴△PDB是等边三角形,
∴∠BDP=∠BPD=∠APC=60°,
∴△ACP是等边三角形,
∵AC=2,PD=3,CH⊥AP,
∴AH=PH=2,BH=PB+PH=3,CH=,
∴BC==,
∵∠CEB=∠CDB=60°,EC是直径,
∴∠CBE=90°,
∴BE=BC tan30°=,
∵EC⊥BF,
∴=,
∵=,
∴=,
∴=,
∴DG=BE=.
15.解:(1)∵=,
∴AB=CD,
在△ABE与△CDE中,,
∴△ABE≌△CDE,
∴BE=DE;
(2)过O作OF⊥AD与F,OG⊥BC于G,连接OA,OC,
根据垂径定理得:AF=FD,BG=OG,
∵AD=BC,
∴AF=CG,
在Rt△AOF与Rt△OCG中,
,
∴Rt△AOF≌Rt△OCG(HL),
∴OF=OG,
∵AD⊥CB,
∴四边形OFEG是正方形,
∴OF=EF,
设OF=EF=x,
则AF=FD=x+1,
∴OF2+AF2=OA2,
即:x2+(x+1)2=52,
解得:x=3,x=﹣4(舍去),
∴AF=4,
∴AE=7.
16.证明(1)∵弦AB=CD,
∴=,
∴﹣=﹣,
即=;
(2)∵=,
∴∠A=∠D,
∴AE=DE.
17.(1)证明:连接AE,DE
∵AB是直径,
∴AE⊥BC,
∵AB=AC,
∴BE=EC,
∵∠CDB=90°,DE是斜边BC的中线,
∴DE=EB,
∴,
即点E是的中点;
(2)设AD=x,则CD=2x,
∴AB=AC=3x,
∵AB为直径,
∴∠ADB=90°,
∴BD2=(3x)2﹣x2=8x2,
在Rt△CDB中,
(2x)2+8x2=122,
∴,
∴,
即⊙O的半径是3.
18.证明:连接OM、ON,
∵O为圆心,M、N分别为弦AB、CD的中点,
∴OM⊥AB,ON⊥CD.
∵AB=CD,
∴OM=ON.
∴∠OMN=∠ONM.
∵∠AMN=90°﹣∠OMN,
∵∠CNM=90°﹣∠ONM,
∴∠AMN=∠CNM.
19.(1)证明:∵AB∥OC,
∴∠C=∠BAC.
∵OA=OC,
∴∠C=∠OAC.
∴∠BAC=∠OAC.
即AC平分∠OAB.
(2)解:∵OE⊥AB,
∴AE=BE=AB=1.
又∵∠AOE=30°,∠PEA=90°,
∴∠OAE=60°.
∴OE=AB cos60°=2×=.
20.证明:(1)如图1,连接AD,BD,
∵C是劣弧AB的中点,
∴∠CDA=∠CDB,
∵DE⊥AB,
∴∠AED=∠DEB=90°,
∴∠A+∠ADE=90°,∠B+∠CDB=90°,
∴∠A=∠B,
∴△ADB为等腰三角形,
∵CD⊥AB,
∴AE=BE;
(2)如图2,延长DB、AP相交于点F,再连接AD,
∵ADBP是圆内接四边形,
∴∠PBF=∠PAD,
∵C是劣弧AB的中点,
∴∠CDA=∠CDF,
∵CD⊥PA,
∴△AFD为等腰三角形,
∴∠F=∠A,AE=EF,
∴∠PBF=∠F,
∴PB=PF,
∴AE=PE+PB
(3)AE=PE﹣PB.
连接AD,BD,AB,DB、AP相交于点F,
∵弧AC=弧BC,
∴∠ADC=∠BDC,
∵CD⊥AP,
∴∠DEA=∠DEF,∠ADE=∠FDE,
∵DE=DE,
∴△DAE≌△DFE,
∴AD=DF,AE=EF,
∴∠DAF=∠DFA,
∴∠DFA=∠PFB,∠PBD=∠DAP,
∴∠PFB=∠PBF,
∴PF=PB,
∴AE=PE﹣PB.
