人教版 五年级数学下册3.3.2 长方体、正方体体积公式的推导课件(19张PPT)
文档属性
| 名称 | 人教版 五年级数学下册3.3.2 长方体、正方体体积公式的推导课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 16:11:49 | ||
图片预览




文档简介
(共19张PPT)
人教版数学五年级(下)
长方体和正方体
第2课时 长方体、正方体体积公式的推导
3
3. 长方体和正方体的体积
1.理解、掌握长方体体积的计算方法的推导过程,体会体积单位的实际意义。
2.猜想、验证、推导长方体体积计算公式,培养学生分析、归纳、推理以及抽象概括的能力。
3.进一步发展学生动手操作能力与空间想象能力。
4.使学生感悟数学知识内在联系的逻辑之美。
学习目标
【重难点】
掌握长方体和正方体的体积计算公式。
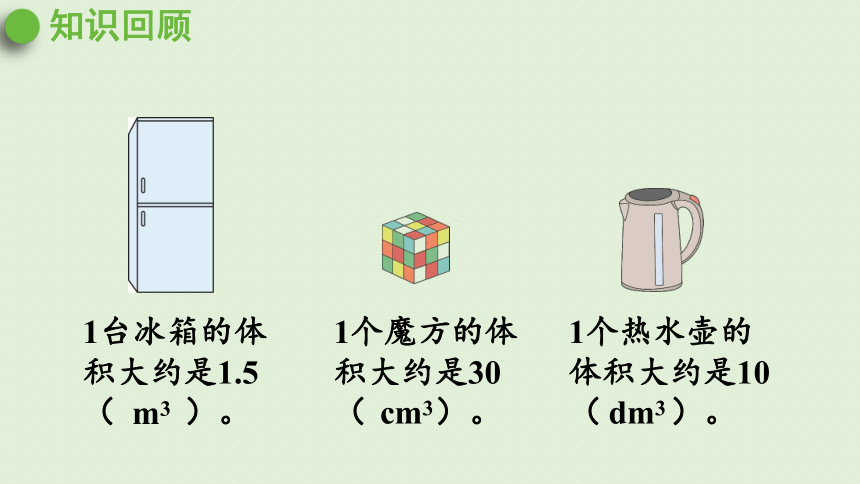
知识回顾
1台冰箱的体积大约是1.5( )。
m3
1个魔方的体积大约是30( )。
cm3
1个热水壶的体积大约是10( )。
dm3
教材第29页
怎样知道一个长方体的体积呢?
课堂导入
像冰箱这样的物品可不能切啊!
如果能把它切成大小相同的小正方体就好了。
能不能先测量,再计算出体积呢?
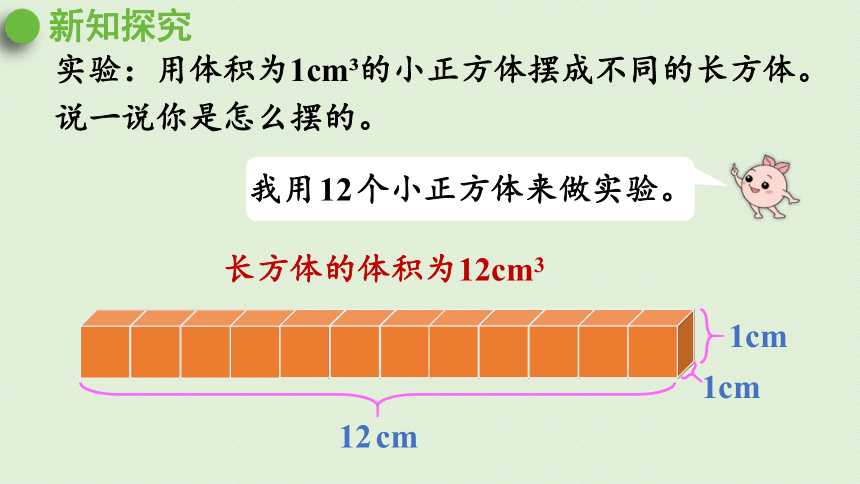
实验:用体积为1cm 的小正方体摆成不同的长方体。说一说你是怎么摆的。
12cm
1cm
1cm
新知探究
我用12个小正方体来做实验。
长方体的体积为12cm3
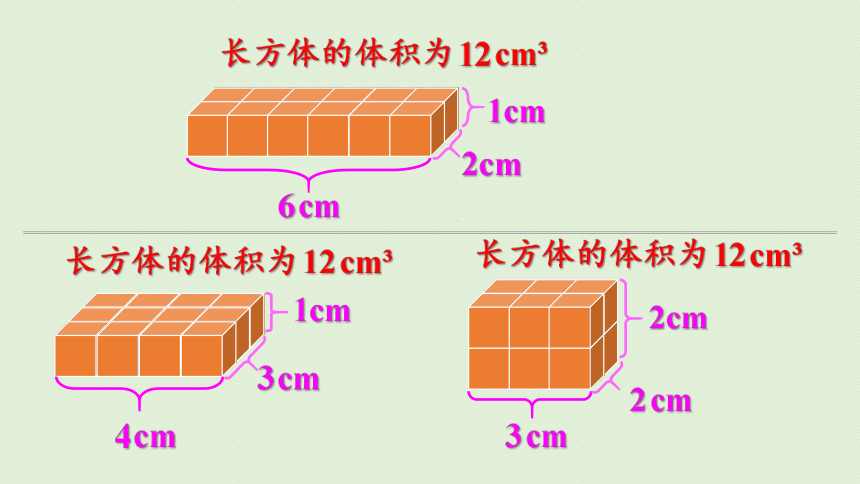
6cm
2cm
1cm
长方体的体积为12cm
4cm
3cm
1cm
长方体的体积为12cm
3cm
2cm
2cm
长方体的体积为12cm
同样多的小正方体摆的长方体的形状不一样,但是长方体的体积都一样。
把摆法不同的长方体的相关数据填入下表。
长 宽 高 小正方体数量 长方体的体积
12cm
1cm
12个
12cm
1cm
6cm
2cm
1cm
12个
12cm
4cm
3cm
1cm
12个
12cm
3cm
2cm
2cm
12个
12cm
观察上表,你发现了什么?
长方体所含体积单位的数量就是长方体的体积。
只要测量出长方体的长、宽、高就能求出长方体的体积。
长
小正方体的数量=
长方体的体积=
每行的个数×行数×层数
宽
高
×
×
12×1×1=12(cm3)
6×2×1=12(cm3)
3×2×2=12(cm3)
4×3×1=12(cm3)
如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:
长方体的体积=长×宽×高
V = abh
根据长方体和正方体的关系,想一想正方体的体积怎样计算。
长方体的体积=长×宽×高
正方体是特殊的长方体,长、宽、高都相等。
正方体的体积
棱长
×
棱长
棱长
=
×
如果用字母V表示正方体的体积,用a表示它的棱长,那么正方体的体积计算公式可以写成:
正方体的体积=棱长×棱长×棱长
V = a · a · a
V = a3
a · a · a也可以写作“a ”,读作“a的立方”,表示3个a相乘。
2 =( ) 52=( ) 10 =( )
8
25
1000
V=a b h
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
计算下面图形的体积。
教材第30页
课堂练习
1.一个长方体包装箱,体积是48dm3,长是4dm,高是3dm,宽是多少分米?
方法一
48÷4÷3
=12÷3
=4(dm)
方法二
解:设长方体的宽是x分米。
(4×3)x=48
12x=48
x=4
答:宽是4厘米。
2.判断题。
(1)棱长是6m的正方体的表面积和体积相等。
( )
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
×
(2) 一个正方体的棱长扩大为原来的2倍,它的体积就扩大为原来的8倍。 ( )
1cm
1cm
1cm
假设棱长为1cm,将棱长扩大2倍为:
1×2=2(cm)
正方体的体积=棱长×棱长×棱长
正方体原来的体积为:1×1×1=1(cm )
正方体扩大后的体积为:2×2×2=8(cm )
8÷1=8
√
课堂小结
体积公式
1.长方体的体积=长×宽×高
V=a b h
2.正方体的体积=棱长×棱长×棱长
V = a3
这节课你有哪些收获?
人教版数学五年级(下)
长方体和正方体
第2课时 长方体、正方体体积公式的推导
3
3. 长方体和正方体的体积
1.理解、掌握长方体体积的计算方法的推导过程,体会体积单位的实际意义。
2.猜想、验证、推导长方体体积计算公式,培养学生分析、归纳、推理以及抽象概括的能力。
3.进一步发展学生动手操作能力与空间想象能力。
4.使学生感悟数学知识内在联系的逻辑之美。
学习目标
【重难点】
掌握长方体和正方体的体积计算公式。
知识回顾
1台冰箱的体积大约是1.5( )。
m3
1个魔方的体积大约是30( )。
cm3
1个热水壶的体积大约是10( )。
dm3
教材第29页
怎样知道一个长方体的体积呢?
课堂导入
像冰箱这样的物品可不能切啊!
如果能把它切成大小相同的小正方体就好了。
能不能先测量,再计算出体积呢?
实验:用体积为1cm 的小正方体摆成不同的长方体。说一说你是怎么摆的。
12cm
1cm
1cm
新知探究
我用12个小正方体来做实验。
长方体的体积为12cm3
6cm
2cm
1cm
长方体的体积为12cm
4cm
3cm
1cm
长方体的体积为12cm
3cm
2cm
2cm
长方体的体积为12cm
同样多的小正方体摆的长方体的形状不一样,但是长方体的体积都一样。
把摆法不同的长方体的相关数据填入下表。
长 宽 高 小正方体数量 长方体的体积
12cm
1cm
12个
12cm
1cm
6cm
2cm
1cm
12个
12cm
4cm
3cm
1cm
12个
12cm
3cm
2cm
2cm
12个
12cm
观察上表,你发现了什么?
长方体所含体积单位的数量就是长方体的体积。
只要测量出长方体的长、宽、高就能求出长方体的体积。
长
小正方体的数量=
长方体的体积=
每行的个数×行数×层数
宽
高
×
×
12×1×1=12(cm3)
6×2×1=12(cm3)
3×2×2=12(cm3)
4×3×1=12(cm3)
如果用字母V表示长方体的体积,用a、b、h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:
长方体的体积=长×宽×高
V = abh
根据长方体和正方体的关系,想一想正方体的体积怎样计算。
长方体的体积=长×宽×高
正方体是特殊的长方体,长、宽、高都相等。
正方体的体积
棱长
×
棱长
棱长
=
×
如果用字母V表示正方体的体积,用a表示它的棱长,那么正方体的体积计算公式可以写成:
正方体的体积=棱长×棱长×棱长
V = a · a · a
V = a3
a · a · a也可以写作“a ”,读作“a的立方”,表示3个a相乘。
2 =( ) 52=( ) 10 =( )
8
25
1000
V=a b h
=7×3×4
=84(cm3)
V=a3
=63
=6×6×6
=216(dm3)
计算下面图形的体积。
教材第30页
课堂练习
1.一个长方体包装箱,体积是48dm3,长是4dm,高是3dm,宽是多少分米?
方法一
48÷4÷3
=12÷3
=4(dm)
方法二
解:设长方体的宽是x分米。
(4×3)x=48
12x=48
x=4
答:宽是4厘米。
2.判断题。
(1)棱长是6m的正方体的表面积和体积相等。
( )
正方体的表面积=棱长×棱长×6
6×6×6=216(m )
正方体的体积=棱长×棱长×棱长
6×6×6=216(m )
表面积和体积是两个不同的概念,单位不一样,不能比较大小。
×
(2) 一个正方体的棱长扩大为原来的2倍,它的体积就扩大为原来的8倍。 ( )
1cm
1cm
1cm
假设棱长为1cm,将棱长扩大2倍为:
1×2=2(cm)
正方体的体积=棱长×棱长×棱长
正方体原来的体积为:1×1×1=1(cm )
正方体扩大后的体积为:2×2×2=8(cm )
8÷1=8
√
课堂小结
体积公式
1.长方体的体积=长×宽×高
V=a b h
2.正方体的体积=棱长×棱长×棱长
V = a3
这节课你有哪些收获?
