29.2三视图---第3课时 课件(共20张PPT)
文档属性
| 名称 | 29.2三视图---第3课时 课件(共20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
29.2三视图
---第3课时
人教版 九年级下
教学目标
能熟练地由三视图想象出物体形状,进一步提高空间想象能力.
(难点)
2. 由三视图想象出立体图形后能进行简单的面积或体积的计算.
(重点)
情境导入
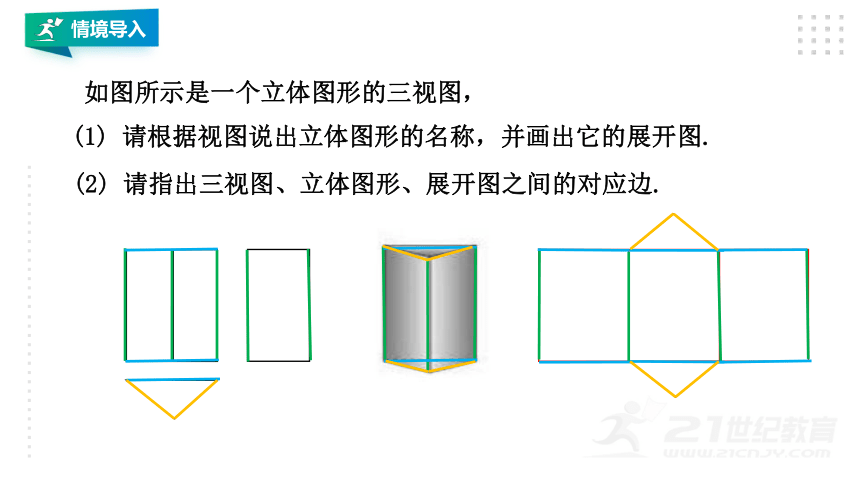
如图所示是一个立体图形的三视图,
(1) 请根据视图说出立体图形的名称,并画出它的展开图.
(2) 请指出三视图、立体图形、展开图之间的对应边.
典例精析
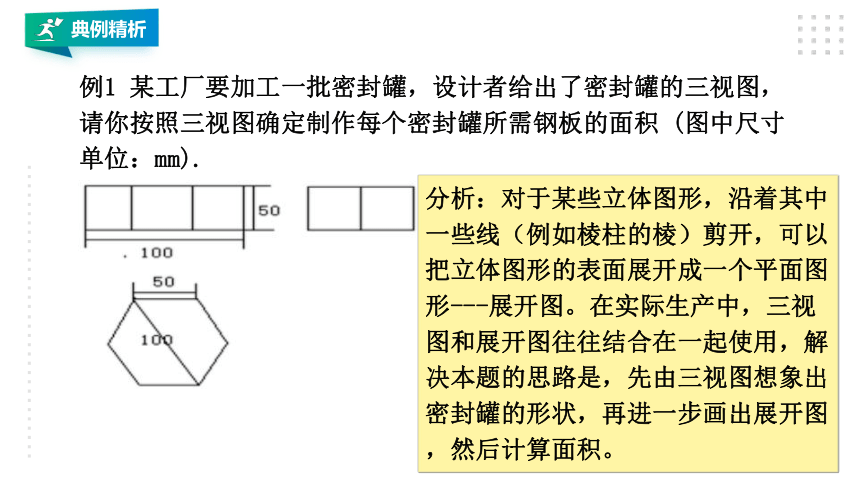
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形---展开图。在实际生产中,三视图和展开图往往结合在一起使用,解决本题的思路是,先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积。
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
典例精析
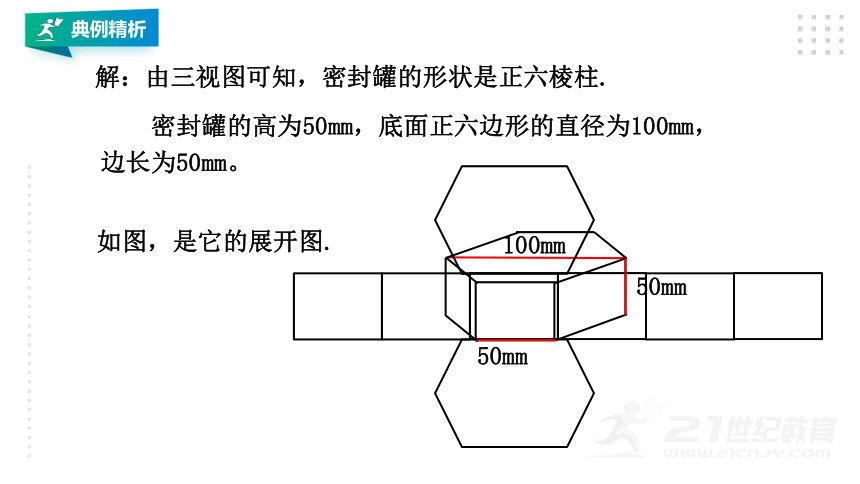
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,
边长为50mm。
100mm
如图,是它的展开图.
典例精析
由展开图可知,制作一个密封罐所需钢板的面积为
典例精析
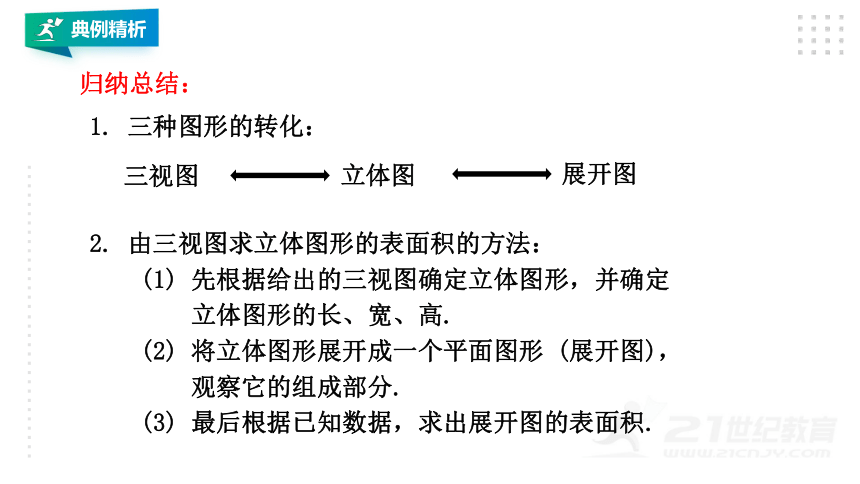
1. 三种图形的转化:
三视图
立体图
展开图
2. 由三视图求立体图形的表面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定
立体图形的长、宽、高.
(2) 将立体图形展开成一个平面图形 (展开图),
观察它的组成部分.
(3) 最后根据已知数据,求出展开图的表面积.
归纳总结:
趁热打铁
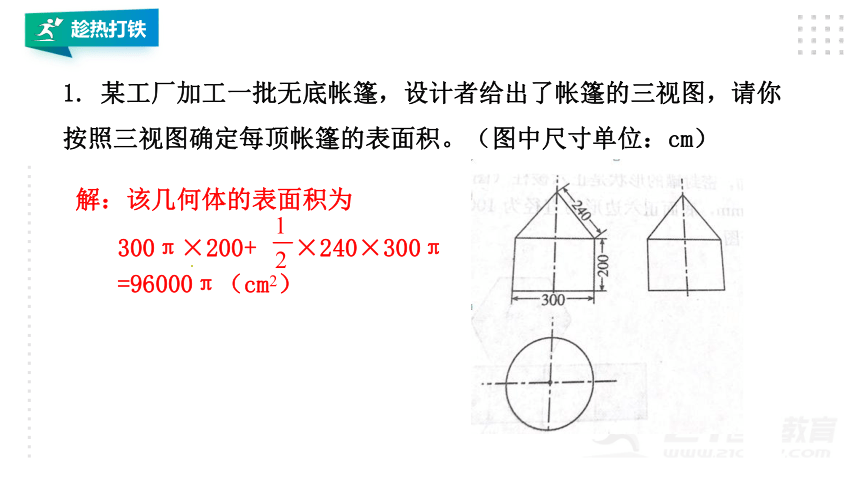
300π×200+ ×240×300π
=96000π(cm2)
1. 某工厂加工一批无底帐篷,设计者给出了帐篷的三视图,请你按照三视图确定每顶帐篷的表面积。(图中尺寸单位:cm)
解:该几何体的表面积为
合作探究
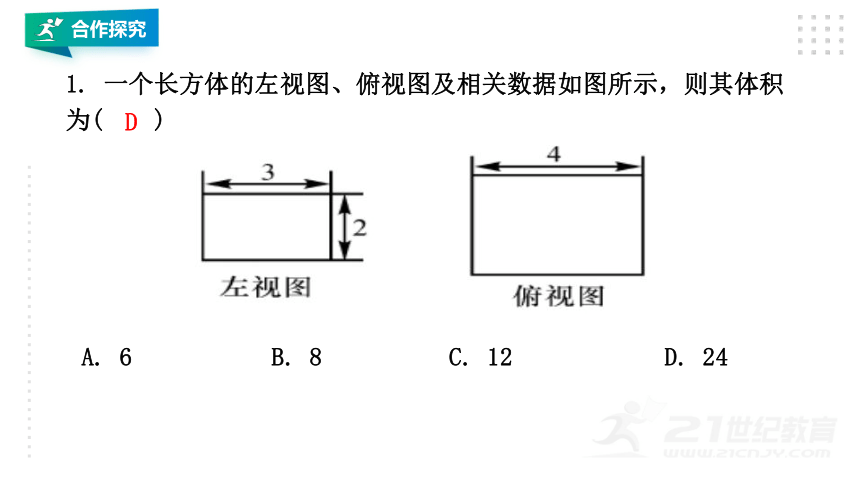
1. 一个长方体的左视图、俯视图及相关数据如图所示,则其体积为( )
A. 6 B. 8 C. 12 D. 24
D
合作探究
2. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的表面积为 .
14 cm2
主视图 左视图 俯视图
3
1
1
合作探究
3. 如图是一个由若干个棱长为1cm的正方体构成的几何体的三视
图.
(1) 请写出构成这个几何体的正方体的个数为 ;
(2) 计算这个几何体的表面积为 .
5
20cm2
主视图 左视图 俯视图
合作探究
4. 如图是某几何体的三视图及相关数据(单位:cm), 则该几何
体的侧面积为 cm2.
2π
合作探究
5、如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.
合作探究
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
表面积为:20×32π+30×40×2+25×40×2+25×30×2
=(5 900+640π)(cm2),
体积为:
25×30×40+102×32π=(30 000+3 200π)(cm3).
提能训练
6. 某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
提能训练
解:由已知可得该几何体是一个下部为圆柱,上部为 球的组合体.由三视图可得下部圆柱的底面半径为1,高为1,则V圆柱=π,上部 球的半径为1,则V 球= × ,故此几何体的体积为 。 .
课堂总结
说一说:
如何根据三视图来求立体图形的体积和表面积?
本节课你有哪些收获?
由三视图求立体图形的体积和表面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
(3) 最后根据已知数据,求出展开图的体积和表面积.
作业布置
习题29.2 P103页:9
https://www.21cnjy.com/help/help_extract.php
29.2三视图
---第3课时
人教版 九年级下
教学目标
能熟练地由三视图想象出物体形状,进一步提高空间想象能力.
(难点)
2. 由三视图想象出立体图形后能进行简单的面积或体积的计算.
(重点)
情境导入
如图所示是一个立体图形的三视图,
(1) 请根据视图说出立体图形的名称,并画出它的展开图.
(2) 请指出三视图、立体图形、展开图之间的对应边.
典例精析
分析:对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形---展开图。在实际生产中,三视图和展开图往往结合在一起使用,解决本题的思路是,先由三视图想象出密封罐的形状,再进一步画出展开图,然后计算面积。
例1 某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积 (图中尺寸单位:mm).
典例精析
解:由三视图可知,密封罐的形状是正六棱柱.
50mm
50mm
密封罐的高为50mm,底面正六边形的直径为100mm,
边长为50mm。
100mm
如图,是它的展开图.
典例精析
由展开图可知,制作一个密封罐所需钢板的面积为
典例精析
1. 三种图形的转化:
三视图
立体图
展开图
2. 由三视图求立体图形的表面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定
立体图形的长、宽、高.
(2) 将立体图形展开成一个平面图形 (展开图),
观察它的组成部分.
(3) 最后根据已知数据,求出展开图的表面积.
归纳总结:
趁热打铁
300π×200+ ×240×300π
=96000π(cm2)
1. 某工厂加工一批无底帐篷,设计者给出了帐篷的三视图,请你按照三视图确定每顶帐篷的表面积。(图中尺寸单位:cm)
解:该几何体的表面积为
合作探究
1. 一个长方体的左视图、俯视图及相关数据如图所示,则其体积为( )
A. 6 B. 8 C. 12 D. 24
D
合作探究
2. 如图是一个几何体的三视图,根据图中提供的数据(单位:cm),可求得这个几何体的表面积为 .
14 cm2
主视图 左视图 俯视图
3
1
1
合作探究
3. 如图是一个由若干个棱长为1cm的正方体构成的几何体的三视
图.
(1) 请写出构成这个几何体的正方体的个数为 ;
(2) 计算这个几何体的表面积为 .
5
20cm2
主视图 左视图 俯视图
合作探究
4. 如图是某几何体的三视图及相关数据(单位:cm), 则该几何
体的侧面积为 cm2.
2π
合作探究
5、如图是一个几何体的三视图,根据所示数据,求该几何体的表面积和体积.
分析:由三视图可知该几何体是由圆柱、长方体组合而成. 分别计算它们的表面积和体积,然后相加即可.
合作探究
解:该图形上、下部分分别是圆柱、长方体,根据图中数据得:
表面积为:20×32π+30×40×2+25×40×2+25×30×2
=(5 900+640π)(cm2),
体积为:
25×30×40+102×32π=(30 000+3 200π)(cm3).
提能训练
6. 某一空间图形的三视图如图所示,其中主视图是半径为1的半圆以及高为 1 的矩形;左视图是半径为1的四分之一圆以及高为1的矩形;俯视图是半径为1的圆,求此图形的体积 (参考公式:V球= πR 3).
提能训练
解:由已知可得该几何体是一个下部为圆柱,上部为 球的组合体.由三视图可得下部圆柱的底面半径为1,高为1,则V圆柱=π,上部 球的半径为1,则V 球= × ,故此几何体的体积为 。 .
课堂总结
说一说:
如何根据三视图来求立体图形的体积和表面积?
本节课你有哪些收获?
由三视图求立体图形的体积和表面积的方法:
(1) 先根据给出的三视图确定立体图形,并确定立体图形的长、宽、高.
(2) 将立体图形展开成一个平面图形 (展开图),观察它的组成部分.
(3) 最后根据已知数据,求出展开图的体积和表面积.
作业布置
习题29.2 P103页:9
https://www.21cnjy.com/help/help_extract.php
