小学数学人教版五年级下9 总复习图形与几何课件(共21张PPT)
文档属性
| 名称 | 小学数学人教版五年级下9 总复习图形与几何课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 11:26:35 | ||
图片预览

文档简介
(共21张PPT)
人教版数学五年级(下)
图形与几何
总复习
9
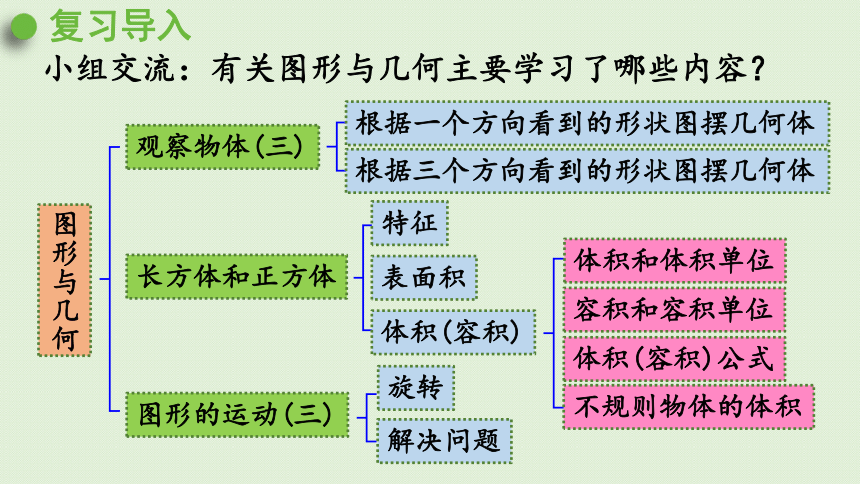
小组交流:有关图形与几何主要学习了哪些内容?
复习导入
图形与几何
观察物体(三)
根据一个方向看到的形状图摆几何体
根据三个方向看到的形状图摆几何体
长方体和正方体
特征
表面积
体积(容积)
体积和体积单位
容积和容积单位
体积(容积)公式
不规则物体的体积
图形的运动(三)
旋转
解决问题
(2)如果从正面看到的图形是 ,左面是 , 上面是 ,则可能是上图所示的( )号几何体。
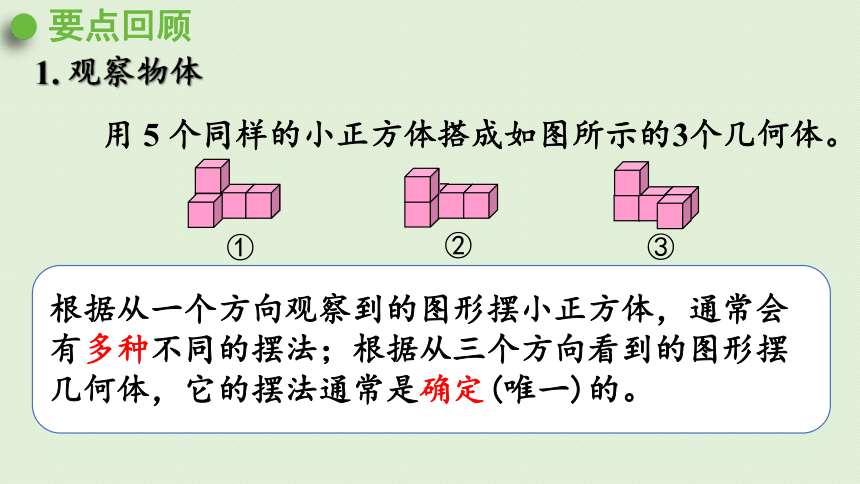
要点回顾
1. 观察物体
用 5 个同样的小正方体搭成如图所示的3个几何体。
①
②
③
(1)如果从正面看到的图形是 ,则可能是上图所示的( )号几何体。
①
②
③
③
根据从一个方向观察到的图形摆小正方体,通常会有多种不同的摆法;根据从三个方向看到的图形摆几何体,它的摆法通常是确定(唯一)的。
①
②
③
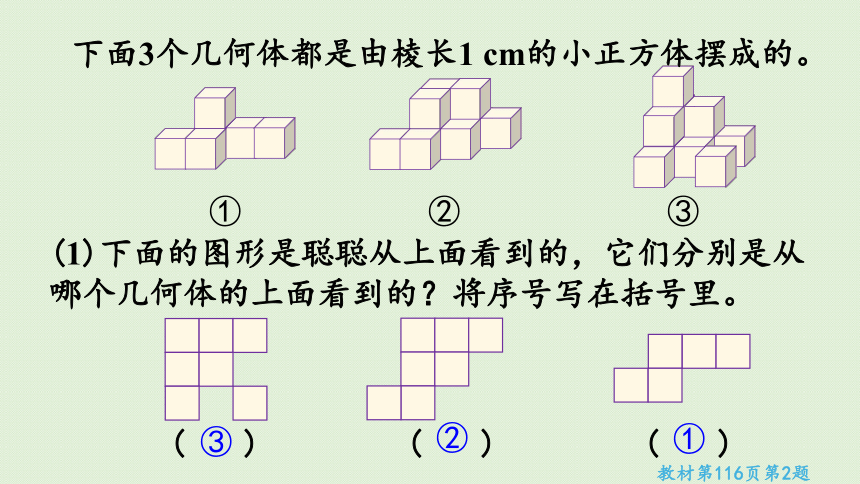
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个几何体的上面看到的?将序号写在括号里。
( )
( )
( )
③
②
①
教材第116页第2题
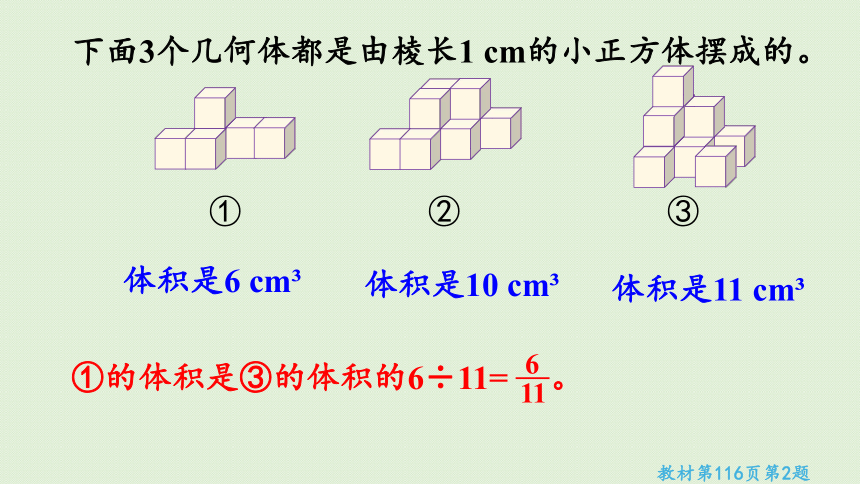
下面3个几何体都是由棱长1 cm的小正方体摆成的。
①
②
③
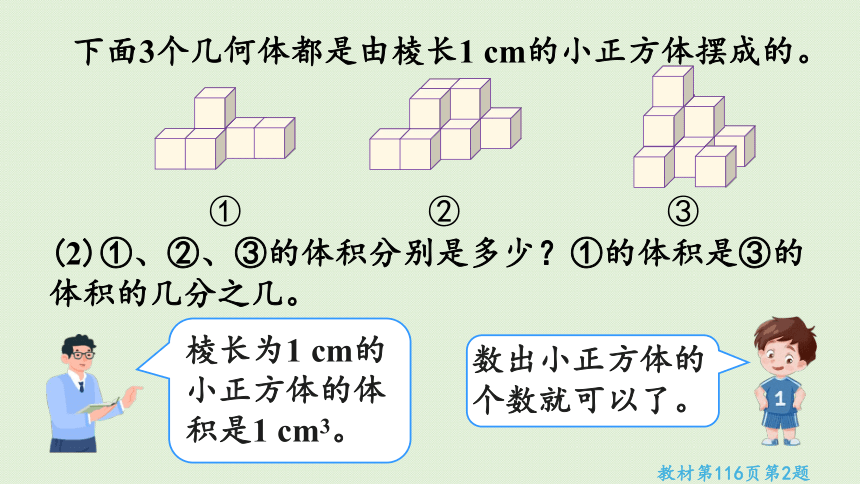
(2)①、②、③的体积分别是多少?①的体积是③的体积的几分之几。
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
棱长为1 cm的小正方体的体积是1 cm3。
数出小正方体的个数就可以了。
①
②
③
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
体积是6 cm
体积是10 cm
体积是11 cm
①的体积是③的体积的6÷11= 。
11
6
①
②
③
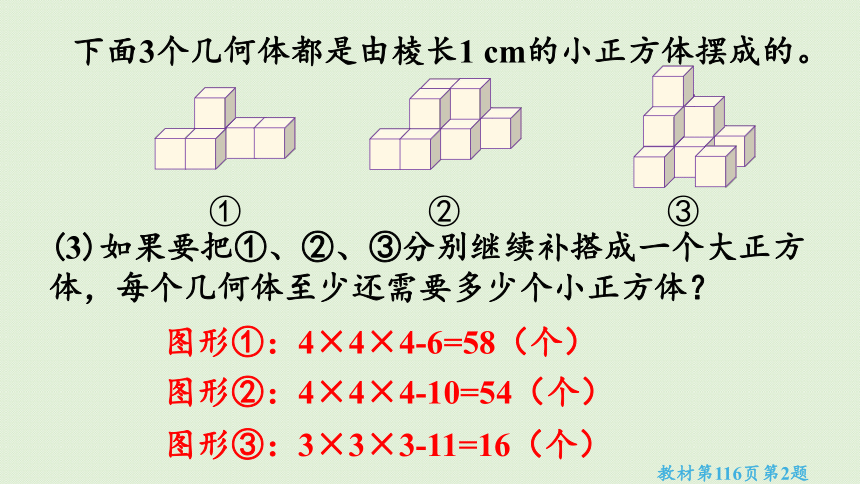
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
①
②
③
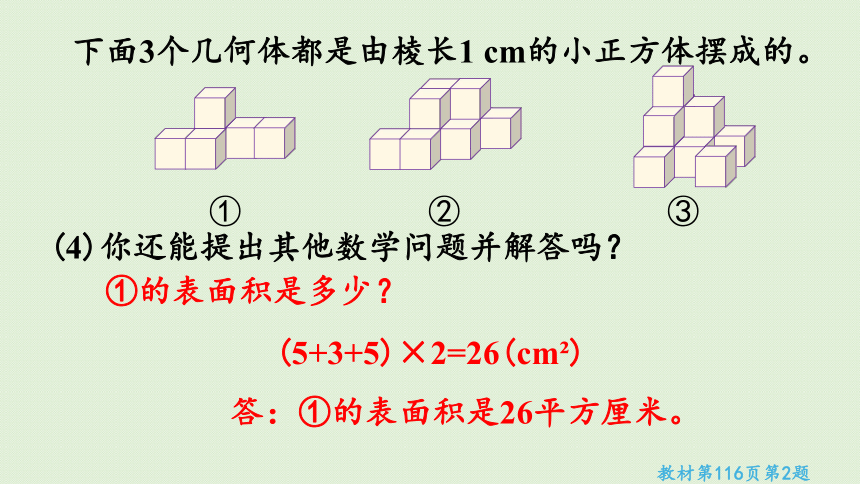
(4)你还能提出其他数学问题并解答吗?
(5+3+5)×2=26(cm )
①的表面积是多少?
答:①的表面积是26平方厘米。
教材第116页第2题
下面3个几何体都是由棱长1 cm的小正方体摆成的。
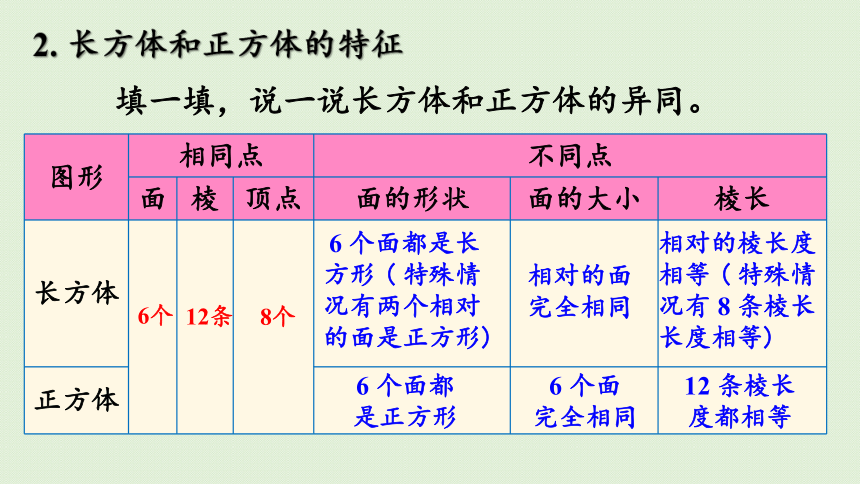
2. 长方体和正方体的特征
填一填,说一说长方体和正方体的异同。
图形 相同点 不同点
面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6 个面都是长方形 ( 特殊情况有两个相对的面是正方形)
相对的面
完全相同
相对的棱长度相等 ( 特殊情况有 8 条棱长长度相等)
6 个面都
是正方形
6 个面
完全相同
12 条棱长度都相等
3. 长方体和正方体的表面积
如图是一个立体图形的展开图(单位:厘米)
10
10
10
5
5
(1)这个展开图可以折成( )体。
(2)折成的立体图形中长度是10cm的棱有( )条,棱长总和是( )cm。
(3)这个立体图形的表面积是( )cm 。
长方
8
120
240
长方体或正方体6个面的总面积,叫做它的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6。
4. 体积与容积
物体所占空间的大小叫做物体的体积。常用的体积单位有m 、dm 、cm 。
容器所能容纳物体的体积,通常叫做它的容积。常用的容积单位有L和mL。
1 m =1000 dm 1 dm =1000 cm
1 L =1000 mL 1 dm = 1 L 1 cm = 1 mL
(2)小长方体的个数 = 每行的个数×行数×层数
长方体的体积 = ( ) × ( ) × ( )
5. 体积(容积)计算公式
填一填,再说一说长方体体积公式的推导过程?
(1)如图所示的长方体是由棱长 1 cm的小正方体拼成的。这个长方体是由( )个这样的小正方体拼成的,它的长是( )cm,宽是( )cm,高是( )cm,它的体积是( )cm 。
30
5
3
2
30
5
3
2
长方体的体积=长×宽×高,用字母表示为:V=abh;正方体的体积=棱长×棱长×棱长,用字母表示:V=a·a·a=a 。长方体(或正方体)的体积=底面积×高,用字母表示: V=Sh。
在解决表面积的实际问题中,要注意求的面的个数。
6. 表面积、体积(容积)的应用
挖一个长8米、宽6米、深2米的蓄水池。
(1)如果给这个蓄水池的底面和四周抹上水泥,抹水泥部分的面积是多少平方米?
思路引导
抹水泥的面积=底面的面积+侧面的面积
规范解答
8×6+(8×2+6×2)×2=104(m )
答:抹水泥部分的面积是104平方米。
在解决体积(容积)的实际问题中,要注意分清求的是体积还是容积。
6. 表面积、体积(容积)的应用
(2)挖这个蓄水池,要挖土多少立方米?
思路引导
挖土的体积 = 蓄水池的容积 = 长×宽×高
规范解答
8×6×2=96(m )
答:要挖土96立方米。
挖一个长8米、宽6米、深2米的蓄水池。
6. 表面积、体积(容积)的应用
(3)蓄水时,当水面离蓄水池顶部还剩0.2 m时就停止进水,这时已经蓄水多少吨?(1 m 的水重1吨)
思路引导
池内水的体积×1吨/m = 已经蓄水的吨数
规范解答
8×6×(2-0.2)×1=86.4(吨)
答:这时已经蓄水86.4吨。
挖一个长8米、宽6米、深2米的蓄水池。
7. 不规则物体体积
说一说,怎样求下面两种物体的体积。
可以把橡皮泥捏成长方体或正方体的形状,再测出相应的长、宽、高或棱长,然后计算出体积。
可以用排水法求出梨的体积。
水面上升的那部分的体
积就是梨的体积。
(1)说一说左图可以通过怎样的变换得到右图。
答:左图可以通过旋转得到右图:
8. 图形的运动
下面的“鱼”可以绕着“鱼嘴”逆时针转动 90°得到;
上面的“鱼”可以绕着“鱼嘴”顺时针转动90°得到。
右边的“鱼”可以绕着“鱼嘴”逆时针转动 180°得到;
图形旋转的三要素:旋转中心、旋转方向和旋转角度。
图形旋转的特征:旋转中心的位置不变,过旋转中心的所有边旋转的方向和角度相同。
图形旋转的性质:旋转后图形的形状、大小不变,只是位置变了。
教材第117页第3题
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多占整个图案的几分之几?。
答:绿色部分占整个图案的 ,红色部分占整个图案的 ,红色部分比绿色部分多占整个图形的 。
3
1
3
2
3
1
8. 图形的运动
教材第117页第3题
练习巩固
1. 填一填。
(1)在( )填上合适的数。
1.06 dm =( )mL 0.08 m =( )dm
3.5 m =( ) L 600 cm =( ) L
1060
80
(2)做一个长8 cm、宽6 cm、高5 cm的长方体框架,至少要用( )厘米的铁丝;如果用彩纸把这个框架包起来,至少需要( )平方厘米的彩纸。
(3)一个正方体容器,从里面量,棱长总和是48厘米,这个容器最多能装水( )毫升。
3500
0.6
76
236
64
2. 选一选。
(1)一个正方体木块,表面积是6平方分米,它的体积是( )。
A. 216立方分米 B. 18立方分米 C. 1立方分米
(2)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加 2 米,新长方体的体积比原来增加( )立方米。
A. 2 ab B. 2 bh C. ab(h+2)
(3)下面三个体积中,与其他两个体积不同的是( )。
6.08 m B. 6080000 cm C. 608 dm
C
C
A
3. 爸爸在一个底面长12分米、宽6分米的鱼缸里放了一个假山石,这时水面上升了3厘米。这个假山石的体积有多大?
思路引导
上升部分的水的体积就是假山石的体积,而上升部分水的体积可以用底面积×上升部分水的高。
规范解答
3厘米=0.3分米
12×6×0.3=21.6(立方分米)
答:这个假山石的体积有21.6立方分米大。
人教版数学五年级(下)
图形与几何
总复习
9
小组交流:有关图形与几何主要学习了哪些内容?
复习导入
图形与几何
观察物体(三)
根据一个方向看到的形状图摆几何体
根据三个方向看到的形状图摆几何体
长方体和正方体
特征
表面积
体积(容积)
体积和体积单位
容积和容积单位
体积(容积)公式
不规则物体的体积
图形的运动(三)
旋转
解决问题
(2)如果从正面看到的图形是 ,左面是 , 上面是 ,则可能是上图所示的( )号几何体。
要点回顾
1. 观察物体
用 5 个同样的小正方体搭成如图所示的3个几何体。
①
②
③
(1)如果从正面看到的图形是 ,则可能是上图所示的( )号几何体。
①
②
③
③
根据从一个方向观察到的图形摆小正方体,通常会有多种不同的摆法;根据从三个方向看到的图形摆几何体,它的摆法通常是确定(唯一)的。
①
②
③
(1)下面的图形是聪聪从上面看到的,它们分别是从哪个几何体的上面看到的?将序号写在括号里。
( )
( )
( )
③
②
①
教材第116页第2题
下面3个几何体都是由棱长1 cm的小正方体摆成的。
①
②
③
(2)①、②、③的体积分别是多少?①的体积是③的体积的几分之几。
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
棱长为1 cm的小正方体的体积是1 cm3。
数出小正方体的个数就可以了。
①
②
③
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
体积是6 cm
体积是10 cm
体积是11 cm
①的体积是③的体积的6÷11= 。
11
6
①
②
③
(3)如果要把①、②、③分别继续补搭成一个大正方体,每个几何体至少还需要多少个小正方体?
下面3个几何体都是由棱长1 cm的小正方体摆成的。
教材第116页第2题
图形①:4×4×4-6=58(个)
图形②:4×4×4-10=54(个)
图形③:3×3×3-11=16(个)
①
②
③
(4)你还能提出其他数学问题并解答吗?
(5+3+5)×2=26(cm )
①的表面积是多少?
答:①的表面积是26平方厘米。
教材第116页第2题
下面3个几何体都是由棱长1 cm的小正方体摆成的。
2. 长方体和正方体的特征
填一填,说一说长方体和正方体的异同。
图形 相同点 不同点
面 棱 顶点 面的形状 面的大小 棱长
长方体
正方体
6个
12条
8个
6 个面都是长方形 ( 特殊情况有两个相对的面是正方形)
相对的面
完全相同
相对的棱长度相等 ( 特殊情况有 8 条棱长长度相等)
6 个面都
是正方形
6 个面
完全相同
12 条棱长度都相等
3. 长方体和正方体的表面积
如图是一个立体图形的展开图(单位:厘米)
10
10
10
5
5
(1)这个展开图可以折成( )体。
(2)折成的立体图形中长度是10cm的棱有( )条,棱长总和是( )cm。
(3)这个立体图形的表面积是( )cm 。
长方
8
120
240
长方体或正方体6个面的总面积,叫做它的表面积。长方体的表面积=(长×宽+长×高+宽×高)×2;正方体的表面积=棱长×棱长×6。
4. 体积与容积
物体所占空间的大小叫做物体的体积。常用的体积单位有m 、dm 、cm 。
容器所能容纳物体的体积,通常叫做它的容积。常用的容积单位有L和mL。
1 m =1000 dm 1 dm =1000 cm
1 L =1000 mL 1 dm = 1 L 1 cm = 1 mL
(2)小长方体的个数 = 每行的个数×行数×层数
长方体的体积 = ( ) × ( ) × ( )
5. 体积(容积)计算公式
填一填,再说一说长方体体积公式的推导过程?
(1)如图所示的长方体是由棱长 1 cm的小正方体拼成的。这个长方体是由( )个这样的小正方体拼成的,它的长是( )cm,宽是( )cm,高是( )cm,它的体积是( )cm 。
30
5
3
2
30
5
3
2
长方体的体积=长×宽×高,用字母表示为:V=abh;正方体的体积=棱长×棱长×棱长,用字母表示:V=a·a·a=a 。长方体(或正方体)的体积=底面积×高,用字母表示: V=Sh。
在解决表面积的实际问题中,要注意求的面的个数。
6. 表面积、体积(容积)的应用
挖一个长8米、宽6米、深2米的蓄水池。
(1)如果给这个蓄水池的底面和四周抹上水泥,抹水泥部分的面积是多少平方米?
思路引导
抹水泥的面积=底面的面积+侧面的面积
规范解答
8×6+(8×2+6×2)×2=104(m )
答:抹水泥部分的面积是104平方米。
在解决体积(容积)的实际问题中,要注意分清求的是体积还是容积。
6. 表面积、体积(容积)的应用
(2)挖这个蓄水池,要挖土多少立方米?
思路引导
挖土的体积 = 蓄水池的容积 = 长×宽×高
规范解答
8×6×2=96(m )
答:要挖土96立方米。
挖一个长8米、宽6米、深2米的蓄水池。
6. 表面积、体积(容积)的应用
(3)蓄水时,当水面离蓄水池顶部还剩0.2 m时就停止进水,这时已经蓄水多少吨?(1 m 的水重1吨)
思路引导
池内水的体积×1吨/m = 已经蓄水的吨数
规范解答
8×6×(2-0.2)×1=86.4(吨)
答:这时已经蓄水86.4吨。
挖一个长8米、宽6米、深2米的蓄水池。
7. 不规则物体体积
说一说,怎样求下面两种物体的体积。
可以把橡皮泥捏成长方体或正方体的形状,再测出相应的长、宽、高或棱长,然后计算出体积。
可以用排水法求出梨的体积。
水面上升的那部分的体
积就是梨的体积。
(1)说一说左图可以通过怎样的变换得到右图。
答:左图可以通过旋转得到右图:
8. 图形的运动
下面的“鱼”可以绕着“鱼嘴”逆时针转动 90°得到;
上面的“鱼”可以绕着“鱼嘴”顺时针转动90°得到。
右边的“鱼”可以绕着“鱼嘴”逆时针转动 180°得到;
图形旋转的三要素:旋转中心、旋转方向和旋转角度。
图形旋转的特征:旋转中心的位置不变,过旋转中心的所有边旋转的方向和角度相同。
图形旋转的性质:旋转后图形的形状、大小不变,只是位置变了。
教材第117页第3题
(2)右图中绿色部分占整个图案的几分之几?红色部分占整个图案的几分之几?红色部分比绿色部分多占整个图案的几分之几?。
答:绿色部分占整个图案的 ,红色部分占整个图案的 ,红色部分比绿色部分多占整个图形的 。
3
1
3
2
3
1
8. 图形的运动
教材第117页第3题
练习巩固
1. 填一填。
(1)在( )填上合适的数。
1.06 dm =( )mL 0.08 m =( )dm
3.5 m =( ) L 600 cm =( ) L
1060
80
(2)做一个长8 cm、宽6 cm、高5 cm的长方体框架,至少要用( )厘米的铁丝;如果用彩纸把这个框架包起来,至少需要( )平方厘米的彩纸。
(3)一个正方体容器,从里面量,棱长总和是48厘米,这个容器最多能装水( )毫升。
3500
0.6
76
236
64
2. 选一选。
(1)一个正方体木块,表面积是6平方分米,它的体积是( )。
A. 216立方分米 B. 18立方分米 C. 1立方分米
(2)一个长方体的长、宽、高分别是a米、b米、h米,如果高增加 2 米,新长方体的体积比原来增加( )立方米。
A. 2 ab B. 2 bh C. ab(h+2)
(3)下面三个体积中,与其他两个体积不同的是( )。
6.08 m B. 6080000 cm C. 608 dm
C
C
A
3. 爸爸在一个底面长12分米、宽6分米的鱼缸里放了一个假山石,这时水面上升了3厘米。这个假山石的体积有多大?
思路引导
上升部分的水的体积就是假山石的体积,而上升部分水的体积可以用底面积×上升部分水的高。
规范解答
3厘米=0.3分米
12×6×0.3=21.6(立方分米)
答:这个假山石的体积有21.6立方分米大。
