小学数学人教版五年级下8.2 稍复杂的找次品问题课件(24张PPT)
文档属性
| 名称 | 小学数学人教版五年级下8.2 稍复杂的找次品问题课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 11:04:58 | ||
图片预览





文档简介
(共24张PPT)
人教版数学五年级(下)
第2课时 稍复杂的找次品问题
数学广角——找次品
8
1. 通过探究,进一步掌握较复杂的找次品的方法,了解稍复杂的找次品问题的解题策略。
2. 运用数学的方法解决生活中的简单问题,培养观察、分析、概括和推理能力。
3. 体会解决问题策略的多样性,初步培养应用意识和解决实际问题的能力,渗透优化思想。
学习目标
【重点】
进一步掌握找次品的方法,运用数学
的方法解决生活中的简单问题。
【难点】
灵活运用找次品的方法解决类似问题。
课堂导入
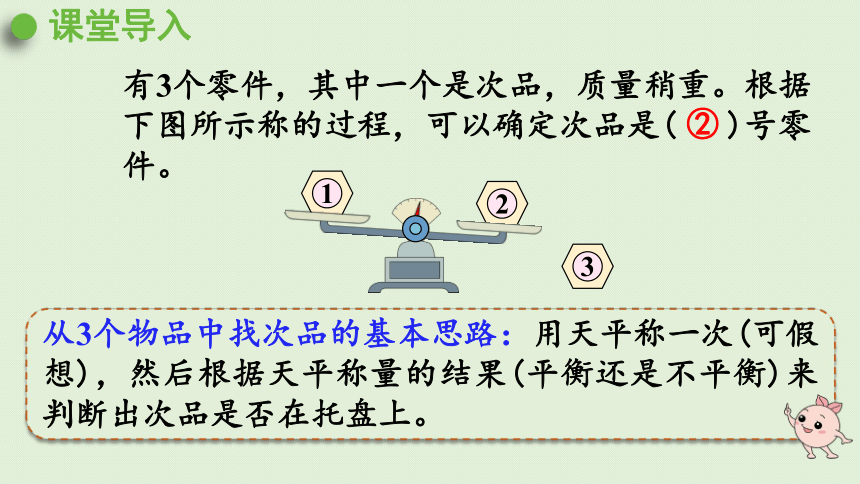
有3个零件,其中一个是次品,质量稍重。根据下图所示称的过程,可以确定次品是( )号零件。
从3个物品中找次品的基本思路:用天平称一次(可假想),然后根据天平称量的结果(平衡还是不平衡)来判断出次品是否在托盘上。
1
2
3
②
新知探究
2
教材第112页例2
8个零件里有1个次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
对,“至少”是指在保证一定能找出次品的各种方法中,称量次数最少的那种方案,不是“运气好”情况下称量的次数。
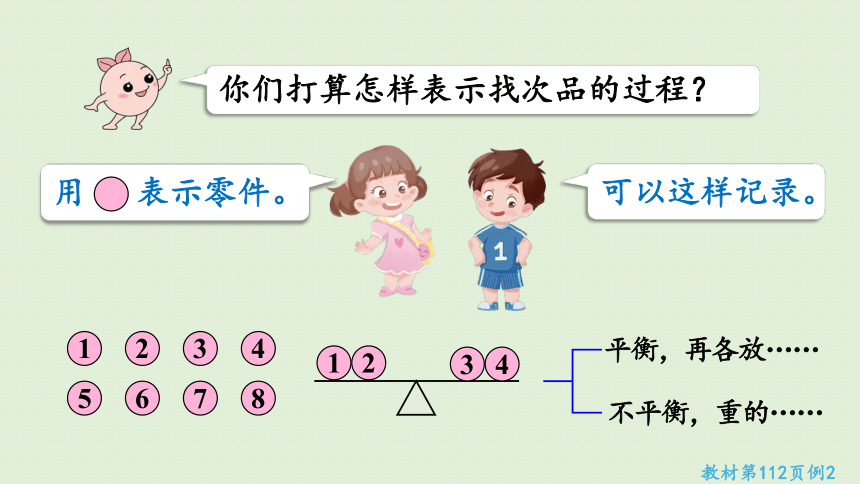
你们打算怎样表示找次品的过程?
可以这样记录。
用 表示零件。
1
2
3
4
5
6
7
8
1
2
3
4
平衡,再各放……
不平衡,重的……
教材第112页例2
小组合作:怎样表示找次品的过程?
合作要求
1.先各自画画示意图,边画边想有哪些不同的方法。
2.组内交流,说说自己的方法和发现。
3.归纳小结,准备全班汇报。
汇报交流。
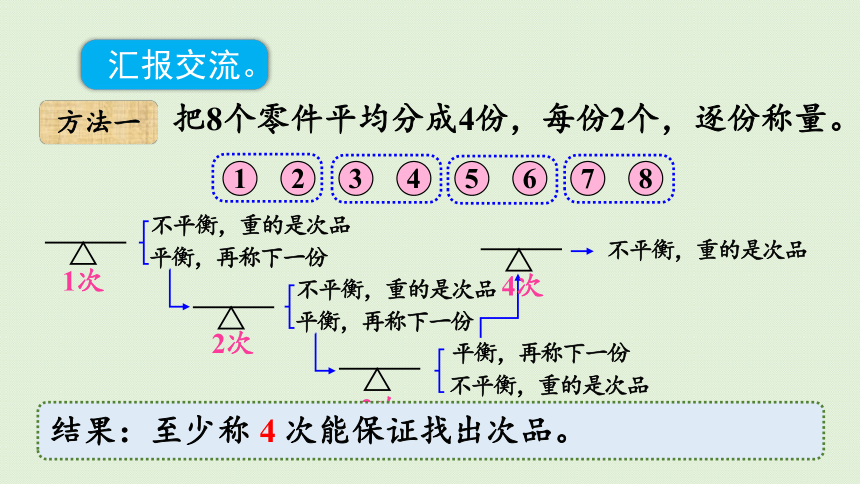
方法一
把8个零件平均分成4份,每份2个,逐份称量。
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
1
2
3
4
5
6
7
8
1次
2次
3次
4次
结果:至少称 4 次能保证找出次品。
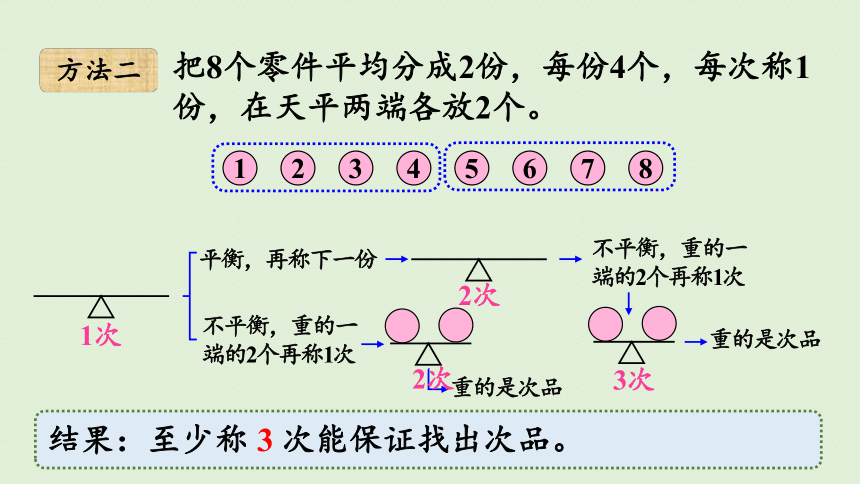
方法二
把8个零件平均分成2份,每份4个,每次称1份,在天平两端各放2个。
1
2
3
4
5
6
7
8
平衡,再称下一份
不平衡,重的一端的2个再称1次
不平衡,重的一端的2个再称1次
重的是次品
重的是次品
结果:至少称 3 次能保证找出次品。
1次
2次
3次
2次
方法三
把8个零件平均分成2份,每份4个,天平两端各放4个。
1
2
3
4
5
6
7
8
不平衡,重的一端的4个再称1次,在两端各放2个。
不平衡,重的一端的2个再称1次,在两端各放1个。
重的是次品
结果:至少称 3 次能保证找出次品。
1次
2次
3次
方法四
把8个零件分成3份:3个、3个、2个,先在天平两端各放3个。
1
2
3
4
5
6
7
8
平衡,次品在另外2个当中。
结果:至少称 2 次能保证找出次品。
不平衡,次品就在重的3个当中。
重的是次品
平衡,剩下的那个是次品。
不平衡,重的是次品。
1次
2次
2次
将称量的情况填入下表。
每次每边放的个数 分成的份数 至少要称的次数
1
4份(2,2,2,2)
4
2
2份(4,4)
3
4
3
2份(4,4)
3
3份(3,3,2)
2
(1)表中哪种方法需要称的次数最少?
把8个零件分成3份(3, 3 ,2)找次品时,需要称的次数最少。
(2)如果9个零件中有一个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?
方法一
把9个零件平均分成3份,每份3个,先在天平两端各放3个称一次。
9
(
3
3
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的3个当中。
(
1
1
,1)
2次
(
1
1
,1)
2次
至少称2次
(2)如果9个零件中有一个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?
方法二
把9个零件分成3份(4,4,1),先在天平两端各放4个称一次。
9
(
4
4
,1)
平衡,另外1个是次品。
不平衡,称重的一端的4个。
1次
(
2
2
,1)
3次
至少称3次
(
1
1
)
不平衡,称重的一端的2个。
平衡,另外1个是次品。
每次每边放的个数 分成的份数 至少要称的次数
每次每边放的个数 分成的份数 至少要称的次数
1
4份(2,2,2,2)
4
2
2份(4,4)
3
4
3
2份(4,4)
3
3份(3,3,2)
2
3
3份(3,3,3)
2
4
3份(4,4,1)
3
(1)你能发现什么?用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
对比从8个零件和9个零件中找次品的过程,发现:分成3份,且每份的数量尽可能相等找次品时,需要称的次数最少。
10
(
3
3
,4)
平衡,次品在另外4个当中。
不平衡,次品就在重的3个当中。
(
1
1
,2)
3次
(
1
1
,1)
2次
平衡,次品在另外2个当中。
(
1
1
)
不平衡,重的是次品
11
(
4
4
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的4个当中。
(
1
1
,1)
2次
(
1
1
,2)
3次
平衡,次品在另外2个当中。
(
1
1
)
不平衡,重的是次品
2次
2次
验证规律。
回顾小结。
利用天平找次品的最优策略:
(1)把待测的物品分成3份;
(2)要分得尽量平均。
能够平均分的就平均分,不能平均分的,也应使最多的一份和最少的一份只相差1。这样能保证找出次品时称量的次数最少。
课堂练习
教材第112页“做一做”
1.
有28瓶水,其中27瓶质量相同,另外1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
做一做
28瓶水
(
9
9
,10)
平衡,盐水在另外10瓶当中。
不平衡,盐水在重的9瓶当中。
至少称3次找出盐水
至少称2次找出盐水
4次
3次
至少称4次
依据上面的结果。
答:至少称4次能保证找出这瓶盐水。
2. 填一填。
(1)用尽可能少的次数找出次品,你会对待测物品进行分组吗?
待测物品个数 6 12 19 25
分组 (2, 2, 2) ( , , ) ( , , ) ( , , )
(2)有5个零件,其中有1个是次品,质量稍重,根据如图所示可以推断出( )号零件一定是正品。
5
1
2
3
4
4
4
4
6
6
7
8
8
9
③
④
⑤
3. 1箱糖果有12袋,其中11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
接着把找的过程表示出来。
称剩下的4袋(1,1,2)
平衡
称剩下的2袋(1,1)
不平衡
轻的一端是次品
称轻的4袋(1,1,2)
平衡
称剩下的2袋(1,1)
不平衡
轻的一端是次品
答:至少称3次能保证找出这袋糖果来。
教材第114页第5题
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
思路引导
可分两步思考:
第一步:找到次品在哪一筒里。
根据3个物品中找1个次品的方法,称1次可确定次品在哪一筒里。
平衡,剩下的那个是次品。
不平衡,重的是次品。
根据12个物品中找1个次品的方法,至少称3次可确定次品是哪一个。
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
思路引导
可分两步思考:
第二步:找到次品网球是哪个。
12个网球
(4, 4, 4)
平衡,称剩下的4个(1, 1, 2)。
平衡,称剩下的2个(1, 1)。
不平衡,重的是次品。
不平衡,称重的4个(1, 1, 2)。
平衡,称剩下的2个(1, 1)。
不平衡,重的是次品。
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
规范解答
根据3个物品中找1个次品的方法,称1次可确定次品在哪一筒里;
根据12个物品中找1个次品的方法,至少称3次可确定次品是哪一个。
所以,至少需要称4次,称3次不能保证找到这个次品。
课堂小结
这节课你有什么收获?
利用天平找次品的最优策略:
(1)把待测物品分成3份,要尽量分得平均,不能够平均分的,也应该使多的一份与少的一份只相差 1 。
(2)用图形、符号等直观方式表示找次品的过程简单、明了。
人教版数学五年级(下)
第2课时 稍复杂的找次品问题
数学广角——找次品
8
1. 通过探究,进一步掌握较复杂的找次品的方法,了解稍复杂的找次品问题的解题策略。
2. 运用数学的方法解决生活中的简单问题,培养观察、分析、概括和推理能力。
3. 体会解决问题策略的多样性,初步培养应用意识和解决实际问题的能力,渗透优化思想。
学习目标
【重点】
进一步掌握找次品的方法,运用数学
的方法解决生活中的简单问题。
【难点】
灵活运用找次品的方法解决类似问题。
课堂导入
有3个零件,其中一个是次品,质量稍重。根据下图所示称的过程,可以确定次品是( )号零件。
从3个物品中找次品的基本思路:用天平称一次(可假想),然后根据天平称量的结果(平衡还是不平衡)来判断出次品是否在托盘上。
1
2
3
②
新知探究
2
教材第112页例2
8个零件里有1个次品(次品重一些)。假如用天平称,至少称几次能保证找出次品?
“至少称几次能保证……”是什么意思?
是指肯定能找出次品的最少次数吧。
对,“至少”是指在保证一定能找出次品的各种方法中,称量次数最少的那种方案,不是“运气好”情况下称量的次数。
你们打算怎样表示找次品的过程?
可以这样记录。
用 表示零件。
1
2
3
4
5
6
7
8
1
2
3
4
平衡,再各放……
不平衡,重的……
教材第112页例2
小组合作:怎样表示找次品的过程?
合作要求
1.先各自画画示意图,边画边想有哪些不同的方法。
2.组内交流,说说自己的方法和发现。
3.归纳小结,准备全班汇报。
汇报交流。
方法一
把8个零件平均分成4份,每份2个,逐份称量。
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
平衡,再称下一份
不平衡,重的是次品
1
2
3
4
5
6
7
8
1次
2次
3次
4次
结果:至少称 4 次能保证找出次品。
方法二
把8个零件平均分成2份,每份4个,每次称1份,在天平两端各放2个。
1
2
3
4
5
6
7
8
平衡,再称下一份
不平衡,重的一端的2个再称1次
不平衡,重的一端的2个再称1次
重的是次品
重的是次品
结果:至少称 3 次能保证找出次品。
1次
2次
3次
2次
方法三
把8个零件平均分成2份,每份4个,天平两端各放4个。
1
2
3
4
5
6
7
8
不平衡,重的一端的4个再称1次,在两端各放2个。
不平衡,重的一端的2个再称1次,在两端各放1个。
重的是次品
结果:至少称 3 次能保证找出次品。
1次
2次
3次
方法四
把8个零件分成3份:3个、3个、2个,先在天平两端各放3个。
1
2
3
4
5
6
7
8
平衡,次品在另外2个当中。
结果:至少称 2 次能保证找出次品。
不平衡,次品就在重的3个当中。
重的是次品
平衡,剩下的那个是次品。
不平衡,重的是次品。
1次
2次
2次
将称量的情况填入下表。
每次每边放的个数 分成的份数 至少要称的次数
1
4份(2,2,2,2)
4
2
2份(4,4)
3
4
3
2份(4,4)
3
3份(3,3,2)
2
(1)表中哪种方法需要称的次数最少?
把8个零件分成3份(3, 3 ,2)找次品时,需要称的次数最少。
(2)如果9个零件中有一个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?
方法一
把9个零件平均分成3份,每份3个,先在天平两端各放3个称一次。
9
(
3
3
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的3个当中。
(
1
1
,1)
2次
(
1
1
,1)
2次
至少称2次
(2)如果9个零件中有一个次品(次品重一些),至少称几次能保证找出次品?是怎么称的?
方法二
把9个零件分成3份(4,4,1),先在天平两端各放4个称一次。
9
(
4
4
,1)
平衡,另外1个是次品。
不平衡,称重的一端的4个。
1次
(
2
2
,1)
3次
至少称3次
(
1
1
)
不平衡,称重的一端的2个。
平衡,另外1个是次品。
每次每边放的个数 分成的份数 至少要称的次数
每次每边放的个数 分成的份数 至少要称的次数
1
4份(2,2,2,2)
4
2
2份(4,4)
3
4
3
2份(4,4)
3
3份(3,3,2)
2
3
3份(3,3,3)
2
4
3份(4,4,1)
3
(1)你能发现什么?用你发现的方法找出10个、11个零件中的1个次品(次品重一些),看看是不是保证找出次品的次数也是最少的。
对比从8个零件和9个零件中找次品的过程,发现:分成3份,且每份的数量尽可能相等找次品时,需要称的次数最少。
10
(
3
3
,4)
平衡,次品在另外4个当中。
不平衡,次品就在重的3个当中。
(
1
1
,2)
3次
(
1
1
,1)
2次
平衡,次品在另外2个当中。
(
1
1
)
不平衡,重的是次品
11
(
4
4
,3)
平衡,次品在另外3个当中。
不平衡,次品就在重的4个当中。
(
1
1
,1)
2次
(
1
1
,2)
3次
平衡,次品在另外2个当中。
(
1
1
)
不平衡,重的是次品
2次
2次
验证规律。
回顾小结。
利用天平找次品的最优策略:
(1)把待测的物品分成3份;
(2)要分得尽量平均。
能够平均分的就平均分,不能平均分的,也应使最多的一份和最少的一份只相差1。这样能保证找出次品时称量的次数最少。
课堂练习
教材第112页“做一做”
1.
有28瓶水,其中27瓶质量相同,另外1瓶是盐水,比其他的水略重一些。至少称几次能保证找出这瓶盐水?
做一做
28瓶水
(
9
9
,10)
平衡,盐水在另外10瓶当中。
不平衡,盐水在重的9瓶当中。
至少称3次找出盐水
至少称2次找出盐水
4次
3次
至少称4次
依据上面的结果。
答:至少称4次能保证找出这瓶盐水。
2. 填一填。
(1)用尽可能少的次数找出次品,你会对待测物品进行分组吗?
待测物品个数 6 12 19 25
分组 (2, 2, 2) ( , , ) ( , , ) ( , , )
(2)有5个零件,其中有1个是次品,质量稍重,根据如图所示可以推断出( )号零件一定是正品。
5
1
2
3
4
4
4
4
6
6
7
8
8
9
③
④
⑤
3. 1箱糖果有12袋,其中11袋质量相同,另有1袋质量不足,轻一些。至少称几次能保证找出这袋糖果来?
接着把找的过程表示出来。
称剩下的4袋(1,1,2)
平衡
称剩下的2袋(1,1)
不平衡
轻的一端是次品
称轻的4袋(1,1,2)
平衡
称剩下的2袋(1,1)
不平衡
轻的一端是次品
答:至少称3次能保证找出这袋糖果来。
教材第114页第5题
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
思路引导
可分两步思考:
第一步:找到次品在哪一筒里。
根据3个物品中找1个次品的方法,称1次可确定次品在哪一筒里。
平衡,剩下的那个是次品。
不平衡,重的是次品。
根据12个物品中找1个次品的方法,至少称3次可确定次品是哪一个。
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
思路引导
可分两步思考:
第二步:找到次品网球是哪个。
12个网球
(4, 4, 4)
平衡,称剩下的4个(1, 1, 2)。
平衡,称剩下的2个(1, 1)。
不平衡,重的是次品。
不平衡,称重的4个(1, 1, 2)。
平衡,称剩下的2个(1, 1)。
不平衡,重的是次品。
有3筒网球,每筒12个,其中有1个次品比正品重一些。若用没有砝码的天平只称3次,找出这个次品,能保证找到吗?
拓展提升
规范解答
根据3个物品中找1个次品的方法,称1次可确定次品在哪一筒里;
根据12个物品中找1个次品的方法,至少称3次可确定次品是哪一个。
所以,至少需要称4次,称3次不能保证找到这个次品。
课堂小结
这节课你有什么收获?
利用天平找次品的最优策略:
(1)把待测物品分成3份,要尽量分得平均,不能够平均分的,也应该使多的一份与少的一份只相差 1 。
(2)用图形、符号等直观方式表示找次品的过程简单、明了。
