函数的概念第一课时

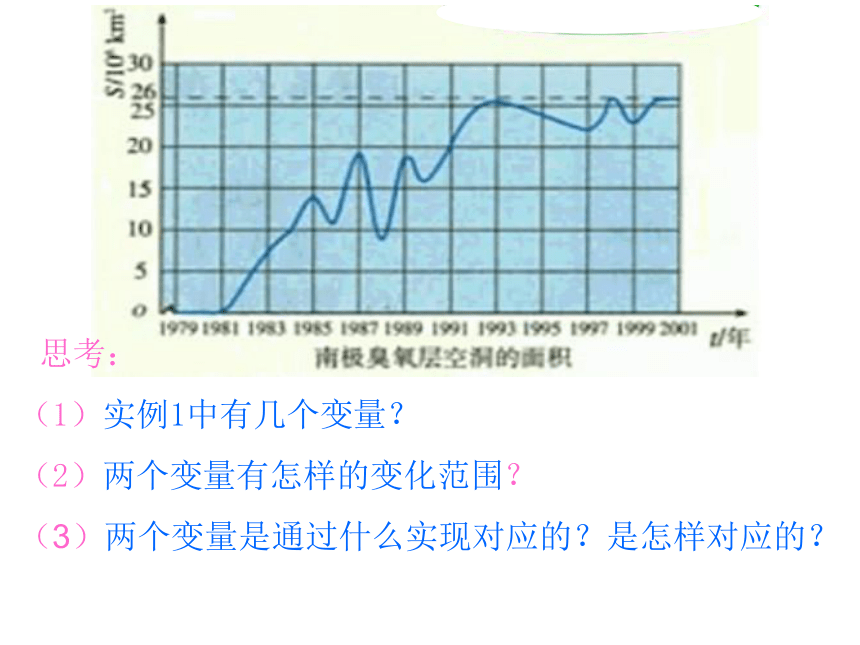
课件18张PPT。函数的概念莱布尼茨（1646-1716）康托尔（1845-1918）李善兰(1811-1882)伟大的数学家1.初中学过的函数的概念是什么？ 设在一个变化过程中有两个变量x和y，如果对于x的每一个取值，y都有唯一确定的值与它对应，则称x是自变量，y是x的函数;其中自变量x的取值集合叫做函数的定义域，和自变量x的值对应的y的值叫做函数值，函数值的取值集合叫做函数的值域。思考：（1）实例1中有几个变量？（2）两个变量有怎样的变化范围？（3）两个变量是通过什么实现对应的？
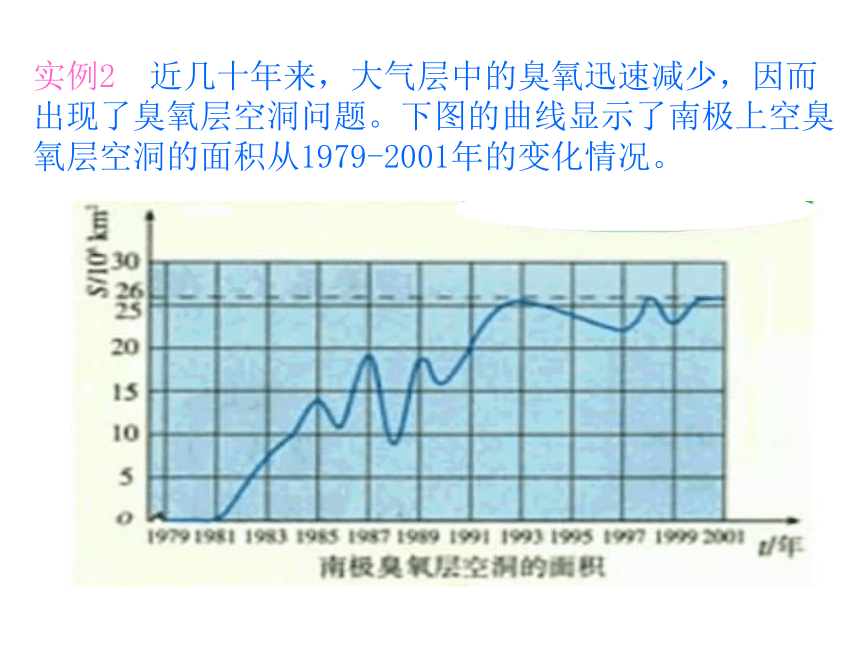
是怎样对应的？实例1。 一枚炮弹发射后，经过26s落到地面击中目标，炮弹的射高为845m，且炮弹距地面的高度h（单位:m）随时间t（单位：s）变化的规律是 。 若变量t的变化范围确定，关系式 也确定，那么高度h的值能确定吗？ 若只有关系式 ，而没有变量t的变化范围，能求出高度h的值吗？ 实例1。 一枚炮弹发射后，经过26s落到地面击中目标，炮弹的射高为845m，且炮弹距地面的高度h（单位:m）随时间t（单位：s）变化的规律是 。不能确定不能实例2 近几十年来，大气层中的臭氧迅速减少，因而出现了臭氧层空洞问题。下图的曲线显示了南极上空臭氧层空洞的面积从1979-2001年的变化情况。（1）实例1中有几个变量？（2）两个变量有怎样的变化范围？（3）两个变量是通过什么实现对应的？是怎样对应的？思考： 若变量t的变化范围确定，图像也确定，那么面积s的值能确定吗？ 若只有图像，而没有确定变量t的值，能求出面积s的值吗？ （4）若只有变量t的变化范围，没有图像，能求出面积s的值吗？不能确定不能实例3 国际上常用恩格尔系数反映一个国家人民生活质量的高低，恩格尔系数越低，生活质量越高。
“八五”计划以来我国城镇居民恩格尔系数变化情况表如下：（1）实例1中有几个变量？（2）两个变量有怎样的变化范围？（3）两个变量是通过什么实现对应的？是怎样对应的？思考： 通过对三个实例的分析，你能说出它们有什么共同点与不同点吗？三个实例中变量之间的关系可以这样来描述： 对于数集A中的每一个x，按照某种对应关系f，在数集B中都有唯一确定的y与之对应，
记作 f:A→B函数的定义：
一般地，设A、B是两个非空数集，如果按照某种对应关系f，对于集合A中的每一个元素x，在集合B中都有唯一确定的元素y与之对应，那么这样的对应叫做从A到B的一个函数，通常记为其中，x叫做自变量，x的取值范围A叫做函数的定义域;与x的值对应的y的值叫做函数值，函数值组成的集合叫做函数y=f(x)的值域。值域是集合B的子集。
理解函数定义1.定义中集合A、B都是非空数集。特别的，定
义域不能为空集，自变量x必须取有意义的值。 2.对应关系f的形式可以是解析式、图像、表格。3.定义域中x的每一个取值，按照确定的对应关系f，都有唯一确定的y值与之对应。 4.集合B中可能存在元素没有对应的x的值，因而值域是集合B的子集。5.函数的三个要素：定义域、对应关系、值域
定义域和对应关系确定了值域6.函数新定义与初中函数定义的区别在于：明确了变量取值范围，强调对应关系；应用集合语言刻画函数的概念。例1 下列说法中，不正确的是（ ）
A.函数值域中的每一个数都有定义域中的一个数与它对应
B.函数的定义域和值域一定是无限集合
C.定义域和对应关系确定后，值域也就确定
D.若函数的定义域中只有一个元素，则值域也只有一个元素.
点评 判断给定的两个变量之间是否具有函数关系的方法
? 定义域和对应关系是否给出？
? 根据所给对应关系，自变量x在定义域中的每一个值，是否都有唯一确定的一个函数值y与之对应？BD1.函数的定义；
2.感知两个变量的依赖关系；
3.对应关系的三种形式；
4.函数的三个要素。