人教版数学四年级下册9数学广角——鸡兔同笼课件(31张PPT)
文档属性
| 名称 | 人教版数学四年级下册9数学广角——鸡兔同笼课件(31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 13:43:24 | ||
图片预览







文档简介
(共31张PPT)
人教版数学四年级(下)
数学广角—鸡兔同笼
9
1.了解“鸡兔同笼”问题的结构特点,掌握用列表法、假设法、方程法解决问题,初步形成解决此类问题的一般性策略。
2.经历猜测的过程,尝试用列表、假设的方法解决“鸡兔同笼”问题。
3.在解决问题的过程中,培养迁移思维能力,感受古代数学问题的趣味性。
学习目标
【重点】
渗透化繁为简的思想,体会用假设法的逻
辑性和一般性。
【难点】
理解用假设法解决“鸡兔同笼”
问题的算理。
课堂导入
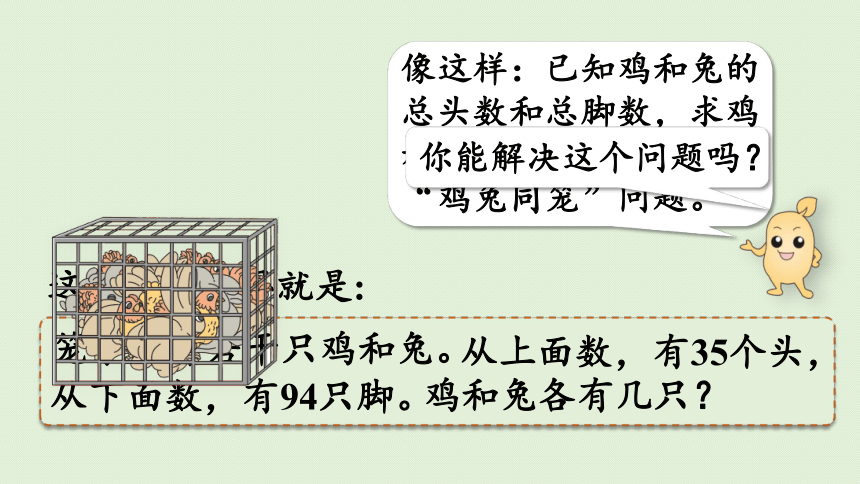
大约一千五百年前,我国古代数学名著《孙子算经》中记载一道数学趣题—“鸡兔同笼”问题。
这道题的意思就是:
从上面数,有35个头,
从下面数,有94只脚。
鸡和兔各有几只?
笼子里有若干只鸡和兔。
像这样:已知鸡和兔的总头数和总脚数,求鸡和兔各有多少只,就是“鸡兔同笼”问题。
你能解决这个问题吗?
想一想:请你试一试,大概有多少只鸡,多少只兔?
100只脚
20只脚
10只鸡
25只兔
+
= 120只脚
×
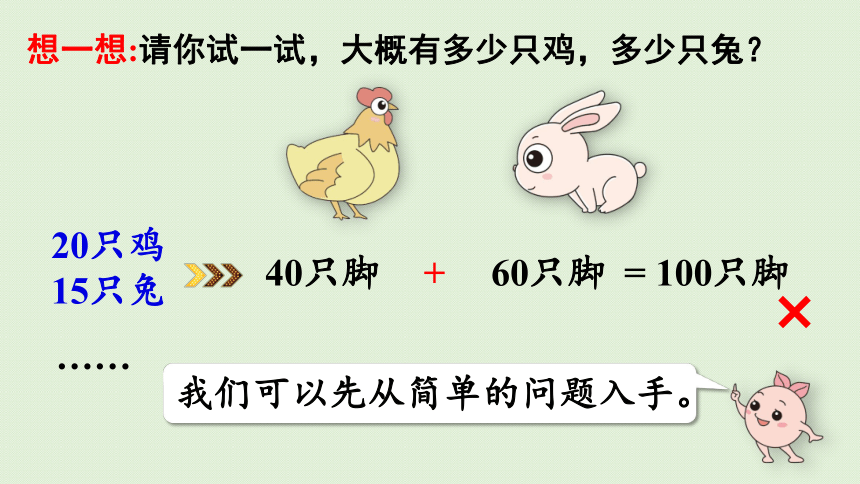
想一想:请你试一试,大概有多少只鸡,多少只兔?
60只脚
40只脚
+
= 100只脚
×
20只鸡
15只兔
我们可以先从简单的问题入手。
……
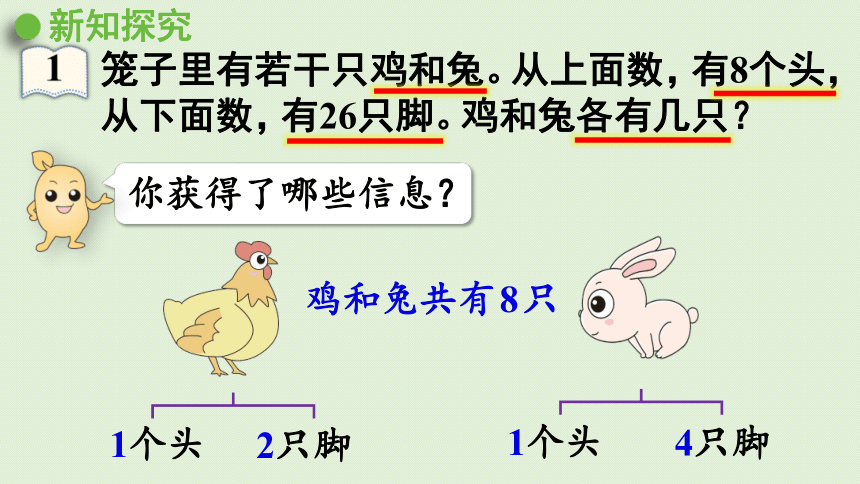
新知探究
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
2只脚
1个头
4只脚
1
鸡和兔共有8只
你获得了哪些信息?
1个头
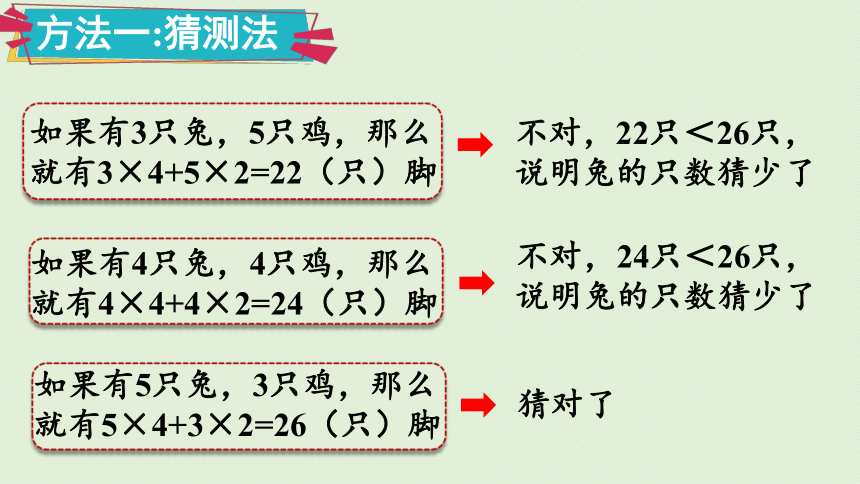
方法一:猜测法
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
不对,22只<26只,说明兔的只数猜少了
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
不对,24只<26只,说明兔的只数猜少了
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
猜对了
鸡
兔
脚
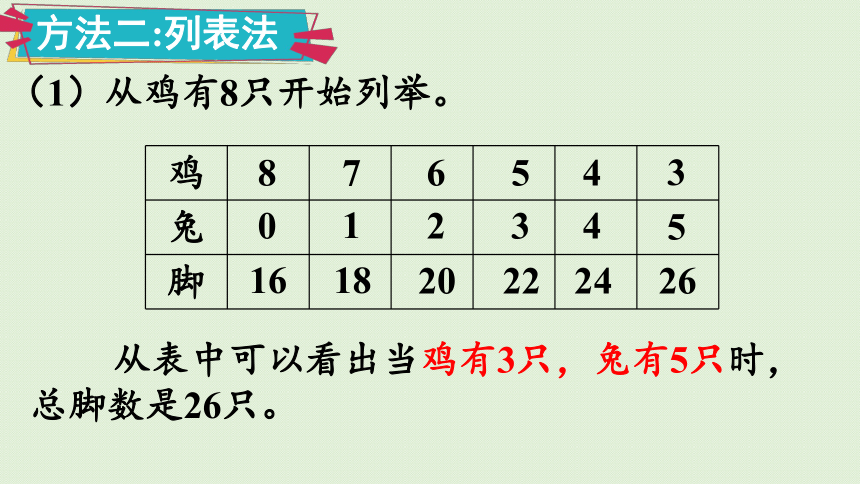
(1)从鸡有8只开始列举。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
方法二:列表法
鸡
兔
脚
(2)从兔有8只开始列举。
8
0
32
1
7
30
2
6
28
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
从鸡和兔分别是总只数的一半(鸡4只、兔4只)开始列举。
鸡
兔
脚
(3)
4
4
24
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
(1)假设笼子里全是鸡。
用 表示头,用 表示脚。
还差26 - 16 = 10(只)脚。
兔有5只,鸡有3只只。
方法三:假设法
每次加2只脚,可以把鸡变成兔。
方法三:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
(2)假设笼子里全是兔。
方法三:假设法
用 表示头,用 表示脚。
还多32 - 26 = 6(只)脚。
鸡有3只,兔有5只。
每次减2只脚,可以把兔变成鸡。
方法三:假设法
设兔得鸡法
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
方法四:抬脚法
鸡抬起一只脚
兔抬起两只脚
1只脚
1个头
2只脚
1个头
这时,每只鸡一只脚,每只兔子两只脚。笼子里只要有一只兔子,脚的总数就比头的总数多1。
方法四:抬脚法
脚的数量是原来的一半
还有94÷2=47只脚
脚的总数-头的数量=兔子的只数。
47-35=12(只)
有35-12=13(只)鸡
方法四:抬脚法
兔的只数:
26÷2-8
=13-8
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”来解决。
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是兔的只数。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
兔的只数:
(94-35×2)÷(4-2)
=24÷2
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法一:假设全是鸡
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
答:兔有12只,鸡有23只。
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法二:假设全是兔
鸡的只数:
(35×4-94)÷(4-2)
=46÷2
=23(只)
兔的只数:
35-23=12(只)
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法三:抬腿法
兔的只数:
94÷2-35
=47-35
=12(只)
鸡的只数:
35-12=23(只)
鸡抬起一只脚,兔子抬起两只脚。
答:兔有12只,鸡有23只。
1.猜测法和列表法:适用于解决数据较小的“鸡兔同笼”问题。
怎样解决“鸡兔同笼”问题?
2.假设法:解决“鸡兔同笼”问题普遍适用的方法。基本数量关系是:
①假设全部是鸡时,兔的只数=(实际总脚数-鸡兔总只数×2)÷(4-2),鸡的总只数=鸡兔总只数-兔的只数。
②假设全部是兔时,鸡的只数=(鸡兔总只数×4-实际总脚数)÷(4-2),兔的总只数=鸡兔总只数-鸡的只数。
3.抬腿法:鸡抬起一只脚,兔子抬起两只脚。
笼子里有一只兔子,脚的总数就比头的总数多1。
脚的总数与头的总数之差就是兔子的只数。
头的总数-兔子的只数=鸡的只数。
课堂练习
1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。
龟、鹤各有多少只?
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
假设全是鹤,鹤的总脚数
鹤的总脚数与实际相差的脚数
每只龟少算了2只脚
龟的只数
(40×4-112)÷(4-2)
=(160-112)÷2
=48÷2
=24(只)
龟的数量:40-24=16 (只)
答:鹤有24只,龟有16只。
假设全是龟,龟的总脚数
龟的总脚数与实际相差的脚数
每只鹤多算了2只脚
鹤的只数
1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。
龟、鹤各有多少只?
2.新星小学“环保小卫士”小分队12人参加植树活动。
男生每人栽了3棵树,女生每人栽了2棵树,一共栽了
32棵树。男、女生各有几人?
(32-12×2)÷(3-2)
=(32-24)÷1
=8÷1
=8(人)
答:男生有8人,女生有4人。
假设全是女生,女生植树的总数
女生植树总棵数与实际相差的棵数
每个男生少算了1棵树
男生的人数
女生的人数:12-8=4 (人)
2.新星小学“环保小卫士”小分队12人参加植树活动。
男生每人栽了3棵树,女生每人栽了2棵树,一共栽了
32棵树。男、女生各有几人?
(12×3-32)÷(3-2)
=(36-32)÷1
=4÷1
=4(人)
假设全是男生,男生植树的总数
男生植树总棵数与实际相差的棵数
每个女生多算了1棵树
女生的人数
男生的人数:12-4=8 (人)
答:男生有8人,女生有4人。
3.全班有54人去公园划船,一共租用了10只船,每只大
船坐6人,每只小船坐4人,且所有的船刚好坐满。租
用的大船和小船分别有多少只?
小船的数量:10-7=3(人)
答:租用的大船有7只,小船有3只。
方法一:假设全是小船
大船的数量:(54-10×4)÷(6-4)
=(54-40)÷2
=14÷2
=7(只)
3.全班有54人去公园划船,一共租用了10只船,每只大
船坐6人,每只小船坐4人,且所有的船刚好坐满。租
用的大船和小船分别有多少只?
答:租用的大船有7只,小船有3只。
方法二:假设全是大船
小船的数量:(10×6-54)÷(6-4)
=(60-54)÷2
=6÷2
=3(只)
大船的数量:10-3=7(人)
课堂小结
鸡兔同笼问题的解题方法
数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量得数量。
还可以用抬腿法解决。
数据较小时,可以用猜想法、列表法解决。
人教版数学四年级(下)
数学广角—鸡兔同笼
9
1.了解“鸡兔同笼”问题的结构特点,掌握用列表法、假设法、方程法解决问题,初步形成解决此类问题的一般性策略。
2.经历猜测的过程,尝试用列表、假设的方法解决“鸡兔同笼”问题。
3.在解决问题的过程中,培养迁移思维能力,感受古代数学问题的趣味性。
学习目标
【重点】
渗透化繁为简的思想,体会用假设法的逻
辑性和一般性。
【难点】
理解用假设法解决“鸡兔同笼”
问题的算理。
课堂导入
大约一千五百年前,我国古代数学名著《孙子算经》中记载一道数学趣题—“鸡兔同笼”问题。
这道题的意思就是:
从上面数,有35个头,
从下面数,有94只脚。
鸡和兔各有几只?
笼子里有若干只鸡和兔。
像这样:已知鸡和兔的总头数和总脚数,求鸡和兔各有多少只,就是“鸡兔同笼”问题。
你能解决这个问题吗?
想一想:请你试一试,大概有多少只鸡,多少只兔?
100只脚
20只脚
10只鸡
25只兔
+
= 120只脚
×
想一想:请你试一试,大概有多少只鸡,多少只兔?
60只脚
40只脚
+
= 100只脚
×
20只鸡
15只兔
我们可以先从简单的问题入手。
……
新知探究
笼子里有若干只鸡和兔。从上面数,有8个头,从下面数,有26只脚。鸡和兔各有几只?
2只脚
1个头
4只脚
1
鸡和兔共有8只
你获得了哪些信息?
1个头
方法一:猜测法
如果有3只兔,5只鸡,那么就有3×4+5×2=22(只)脚
不对,22只<26只,说明兔的只数猜少了
如果有4只兔,4只鸡,那么就有4×4+4×2=24(只)脚
不对,24只<26只,说明兔的只数猜少了
如果有5只兔,3只鸡,那么就有5×4+3×2=26(只)脚
猜对了
鸡
兔
脚
(1)从鸡有8只开始列举。
8
0
16
7
1
18
6
2
20
5
3
22
4
4
24
3
5
26
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
方法二:列表法
鸡
兔
脚
(2)从兔有8只开始列举。
8
0
32
1
7
30
2
6
28
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
从鸡和兔分别是总只数的一半(鸡4只、兔4只)开始列举。
鸡
兔
脚
(3)
4
4
24
3
5
26
方法二:列表法
从表中可以看出当鸡有3只,兔有5只时,总脚数是26只。
(1)假设笼子里全是鸡。
用 表示头,用 表示脚。
还差26 - 16 = 10(只)脚。
兔有5只,鸡有3只只。
方法三:假设法
每次加2只脚,可以把鸡变成兔。
方法三:假设法
设鸡得兔法
兔的只数:
(26-8×2)÷(4-2)
=10÷2
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
(2)假设笼子里全是兔。
方法三:假设法
用 表示头,用 表示脚。
还多32 - 26 = 6(只)脚。
鸡有3只,兔有5只。
每次减2只脚,可以把兔变成鸡。
方法三:假设法
设兔得鸡法
答:兔有5只,鸡有3只。
(1)假设笼子里全是鸡。
鸡的只数:
(8×4-26)÷(4-2)
=6÷2
=3(只)
兔的只数:
8 - 3 = 5(只)
方法四:抬脚法
鸡抬起一只脚
兔抬起两只脚
1只脚
1个头
2只脚
1个头
这时,每只鸡一只脚,每只兔子两只脚。笼子里只要有一只兔子,脚的总数就比头的总数多1。
方法四:抬脚法
脚的数量是原来的一半
还有94÷2=47只脚
脚的总数-头的数量=兔子的只数。
47-35=12(只)
有35-12=13(只)鸡
方法四:抬脚法
兔的只数:
26÷2-8
=13-8
=5(只)
鸡的只数:
8 - 5 = 3(只)
答:兔有5只,鸡有3只。
猜测法和列表法效率低。对于数据较大的“鸡兔同笼”问题,一般用假设法来解决,也可以用“抬脚法”来解决。
当用假设法解决“鸡兔同笼”问题时,假设全是鸡,先算出的是兔的只数;假设全是兔,先算出的是兔的只数。
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
兔的只数:
(94-35×2)÷(4-2)
=24÷2
=12(只)
鸡的只数:
35-12=23(只)
答:兔有12只,鸡有23只。
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法一:假设全是鸡
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
答:兔有12只,鸡有23只。
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法二:假设全是兔
鸡的只数:
(35×4-94)÷(4-2)
=46÷2
=23(只)
兔的只数:
35-23=12(只)
笼子里有若干只鸡和兔。从上面数,有35个头,从下面数,有94只脚。鸡和兔各有几只?
你能竖着用上面的方法解决前面的“鸡兔同笼”问题吗?
方法三:抬腿法
兔的只数:
94÷2-35
=47-35
=12(只)
鸡的只数:
35-12=23(只)
鸡抬起一只脚,兔子抬起两只脚。
答:兔有12只,鸡有23只。
1.猜测法和列表法:适用于解决数据较小的“鸡兔同笼”问题。
怎样解决“鸡兔同笼”问题?
2.假设法:解决“鸡兔同笼”问题普遍适用的方法。基本数量关系是:
①假设全部是鸡时,兔的只数=(实际总脚数-鸡兔总只数×2)÷(4-2),鸡的总只数=鸡兔总只数-兔的只数。
②假设全部是兔时,鸡的只数=(鸡兔总只数×4-实际总脚数)÷(4-2),兔的总只数=鸡兔总只数-鸡的只数。
3.抬腿法:鸡抬起一只脚,兔子抬起两只脚。
笼子里有一只兔子,脚的总数就比头的总数多1。
脚的总数与头的总数之差就是兔子的只数。
头的总数-兔子的只数=鸡的只数。
课堂练习
1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。
龟、鹤各有多少只?
(112-40×2)÷(4-2)
=(112-80)÷2
=32÷2
=16(只)
鹤的数量:40-16=24(只)
假设全是鹤,鹤的总脚数
鹤的总脚数与实际相差的脚数
每只龟少算了2只脚
龟的只数
(40×4-112)÷(4-2)
=(160-112)÷2
=48÷2
=24(只)
龟的数量:40-24=16 (只)
答:鹤有24只,龟有16只。
假设全是龟,龟的总脚数
龟的总脚数与实际相差的脚数
每只鹤多算了2只脚
鹤的只数
1.有龟和鹤共40只,龟的腿和鹤的腿共有112条。
龟、鹤各有多少只?
2.新星小学“环保小卫士”小分队12人参加植树活动。
男生每人栽了3棵树,女生每人栽了2棵树,一共栽了
32棵树。男、女生各有几人?
(32-12×2)÷(3-2)
=(32-24)÷1
=8÷1
=8(人)
答:男生有8人,女生有4人。
假设全是女生,女生植树的总数
女生植树总棵数与实际相差的棵数
每个男生少算了1棵树
男生的人数
女生的人数:12-8=4 (人)
2.新星小学“环保小卫士”小分队12人参加植树活动。
男生每人栽了3棵树,女生每人栽了2棵树,一共栽了
32棵树。男、女生各有几人?
(12×3-32)÷(3-2)
=(36-32)÷1
=4÷1
=4(人)
假设全是男生,男生植树的总数
男生植树总棵数与实际相差的棵数
每个女生多算了1棵树
女生的人数
男生的人数:12-4=8 (人)
答:男生有8人,女生有4人。
3.全班有54人去公园划船,一共租用了10只船,每只大
船坐6人,每只小船坐4人,且所有的船刚好坐满。租
用的大船和小船分别有多少只?
小船的数量:10-7=3(人)
答:租用的大船有7只,小船有3只。
方法一:假设全是小船
大船的数量:(54-10×4)÷(6-4)
=(54-40)÷2
=14÷2
=7(只)
3.全班有54人去公园划船,一共租用了10只船,每只大
船坐6人,每只小船坐4人,且所有的船刚好坐满。租
用的大船和小船分别有多少只?
答:租用的大船有7只,小船有3只。
方法二:假设全是大船
小船的数量:(10×6-54)÷(6-4)
=(60-54)÷2
=6÷2
=3(只)
大船的数量:10-3=7(人)
课堂小结
鸡兔同笼问题的解题方法
数据较大时,用假设法比较普遍,假设全部是某一种量,先求出的就是另一种量得数量。
还可以用抬腿法解决。
数据较小时,可以用猜想法、列表法解决。
