2020-2021学年高二下学期数学人教版(2019)选择性必修第二册4.1数列的概念(第二课时)课件册(共20张PPT)
文档属性
| 名称 | 2020-2021学年高二下学期数学人教版(2019)选择性必修第二册4.1数列的概念(第二课时)课件册(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 525.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 15:58:18 | ||
图片预览







文档简介
(共20张PPT)
第四章 数列
4.1 数列的概念(第二课时)
数列的通项公式与递推公式
复习旧知
情境引入
例3 如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
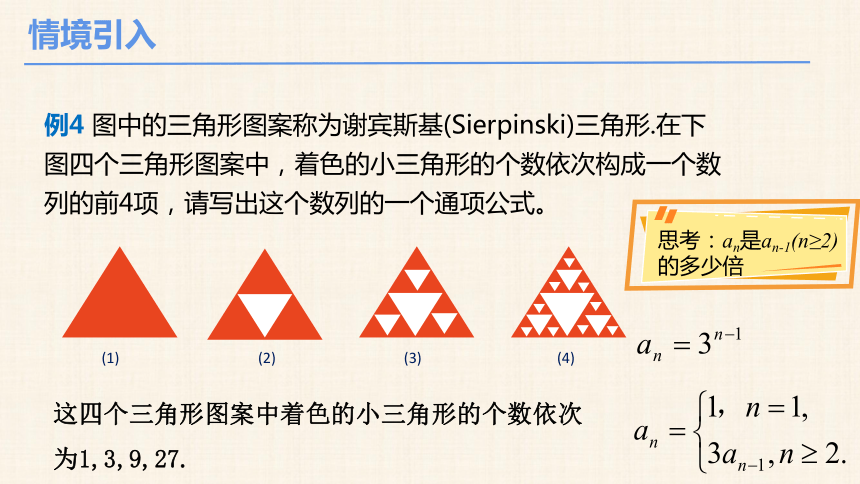
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
情境引入
思考:an是an-1(n≥2)的多少倍
像 这样,如果一个数列的相邻两项或多项之间可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项和递推公式,就能求出数列的每一项了
一、递推公式定义:
相同点 不同点
通项公式 均可确定一个数列,求出数列中的任意一项 给出n的值,可求出数列中的第n项an
递推公式 由前一项(或前几项),通过一次(或多次)运算,可求出第n项an
思考:数列的递推公式与其通项公式有何异同?
二、 由递推公式写出数列的项
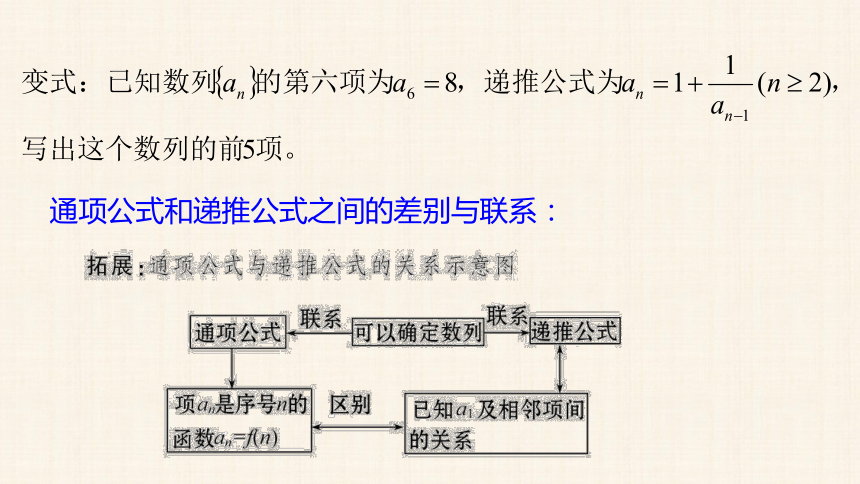
通项公式和递推公式之间的差别与联系:
例1:已知下列数列的递推公式,写出此数列的前 4 项,并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
题型一 已知数列的递推公式,求前几项并猜出通项公式
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,
可归纳出an=(n-1)2.
课本P8练习2
三、 数列的前n项和
注意:(1)已知数列{an}的前n项和Sn,求an,一般使用公式an=Sn-Sn-1(n≥2),
但必须注意它成立的条件(n≥2且n∈N*).
(2)由Sn-Sn-1求得的an,若当n=1时,a1的值不等于S1的值,
则数列的通项公式应采用分段表示,即
练:已知数列{an}的前n项和Sn=n2+2,求数列{an}的通项公式.
解:a1=S1=1+2=3,①
而n≥2时,an=Sn-Sn-1=(n2+2)-[(n-1)2+2]=2n-1.②
在②中,当n=1时,2×1-1=1,故a1不适合②式.∴数列{an}的通项公式为
已知数列{an}的前n项和Sn,求通项公式的步骤:
(1)当n=1时,a1=S1.
(2)当n≥2时,根据Sn写出Sn-1,化简an=Sn-Sn-1.
(3)如果a1也满足当n≥2时,an=Sn-Sn-1的式子,
那么数列{an}的通项公式为an=Sn-Sn-1;
如果a1不满足当n≥2时,an=Sn-Sn-1的式子,
那么数列{an}的通项公式要分段表示为
类题通法
当堂检测
答案:C
B
2.已知数列{an},an-1=man+1(n>1),且a2=3,a3=5,则实数m等于( )
A.0 B.
C.2 D.5
3.若数列{an}的通项公式为an=-2n2+25n,则数列{an}的各项中最大项是( )
A.第4项 B.第5项
C.第6项 D.第7项
答案:C
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数列{an}的通项公式.
题型二 已知数列的递推公式,用累加法求通项公式
an=3n+2.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
a2=a1+3
a3=a2+3
a4=a3+3
…………
an-1=an-2+3(n≥2)
an=an-1+3
累加得:
a2+a3+a4+…+an-1+an=a1+a2+a3+an-1+3(n-1)
例3:已知a1=2,an+1=2an,求an.
题型三 已知数列的递推公式,用累乘法求通项公式
感 谢 聆 听
第四章 数列
4.1 数列的概念(第二课时)
数列的通项公式与递推公式
复习旧知
情境引入
例3 如果数列的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
例4 图中的三角形图案称为谢宾斯基(Sierpinski)三角形.在下图四个三角形图案中,着色的小三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式。
(1)
(2)
(3)
(4)
这四个三角形图案中着色的小三角形的个数依次为1,3,9,27.
情境引入
思考:an是an-1(n≥2)的多少倍
像 这样,如果一个数列的相邻两项或多项之间可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.知道了首项和递推公式,就能求出数列的每一项了
一、递推公式定义:
相同点 不同点
通项公式 均可确定一个数列,求出数列中的任意一项 给出n的值,可求出数列中的第n项an
递推公式 由前一项(或前几项),通过一次(或多次)运算,可求出第n项an
思考:数列的递推公式与其通项公式有何异同?
二、 由递推公式写出数列的项
通项公式和递推公式之间的差别与联系:
例1:已知下列数列的递推公式,写出此数列的前 4 项,并推测数列的通项公式.
(1)数列{an}满足 an+1=2an+1,n∈N*,且 a1=-1;
(2)在数列{an}中,a1=1,an=an-1+
1
n(n-1)
(n≥2).
题型一 已知数列的递推公式,求前几项并猜出通项公式
练习1 根据递推公式,分别写出它的前 5 项,并归纳出通项公式:
(1)a1=0,an+1=an+(2n-1)(n∈N*);
(2)a1=1,an+1=
2an
an+2
(n∈N*).
解:(1)a1=0,a2=a1+1=1,a3=a2+3=4,
a4=a3+5=9,a5=a4+7=16.
由a1=02,a2=12,a3=22,a4=32,a5=42,
可归纳出an=(n-1)2.
课本P8练习2
三、 数列的前n项和
注意:(1)已知数列{an}的前n项和Sn,求an,一般使用公式an=Sn-Sn-1(n≥2),
但必须注意它成立的条件(n≥2且n∈N*).
(2)由Sn-Sn-1求得的an,若当n=1时,a1的值不等于S1的值,
则数列的通项公式应采用分段表示,即
练:已知数列{an}的前n项和Sn=n2+2,求数列{an}的通项公式.
解:a1=S1=1+2=3,①
而n≥2时,an=Sn-Sn-1=(n2+2)-[(n-1)2+2]=2n-1.②
在②中,当n=1时,2×1-1=1,故a1不适合②式.∴数列{an}的通项公式为
已知数列{an}的前n项和Sn,求通项公式的步骤:
(1)当n=1时,a1=S1.
(2)当n≥2时,根据Sn写出Sn-1,化简an=Sn-Sn-1.
(3)如果a1也满足当n≥2时,an=Sn-Sn-1的式子,
那么数列{an}的通项公式为an=Sn-Sn-1;
如果a1不满足当n≥2时,an=Sn-Sn-1的式子,
那么数列{an}的通项公式要分段表示为
类题通法
当堂检测
答案:C
B
2.已知数列{an},an-1=man+1(n>1),且a2=3,a3=5,则实数m等于( )
A.0 B.
C.2 D.5
3.若数列{an}的通项公式为an=-2n2+25n,则数列{an}的各项中最大项是( )
A.第4项 B.第5项
C.第6项 D.第7项
答案:C
例2:已知在数列{an}中,a1=5,an=an-1+3(n≥2),求数列{an}的通项公式.
题型二 已知数列的递推公式,用累加法求通项公式
an=3n+2.
总结归纳:若数列有形如an+1=an+f(n)的递推公式,且可求 f(1)+f(2)+…+f(n),可用累加法求通项公式.
a2=a1+3
a3=a2+3
a4=a3+3
…………
an-1=an-2+3(n≥2)
an=an-1+3
累加得:
a2+a3+a4+…+an-1+an=a1+a2+a3+an-1+3(n-1)
例3:已知a1=2,an+1=2an,求an.
题型三 已知数列的递推公式,用累乘法求通项公式
感 谢 聆 听
