2021-2022学年高一上学期数学人教A版(2019)必修第一册5.5.1第三课时二倍角的正弦余弦正切公式课件(共21张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.5.1第三课时二倍角的正弦余弦正切公式课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-16 16:05:28 | ||
图片预览








文档简介
(共21张PPT)
5.5.1 二倍角的正弦、余弦、正切公式
回顾和引入
PART 01
复习回顾
前面我们学习了:
由以上公式,你能推导出?
新课讲授
PART 02
探究:探究公式
自主探究展示
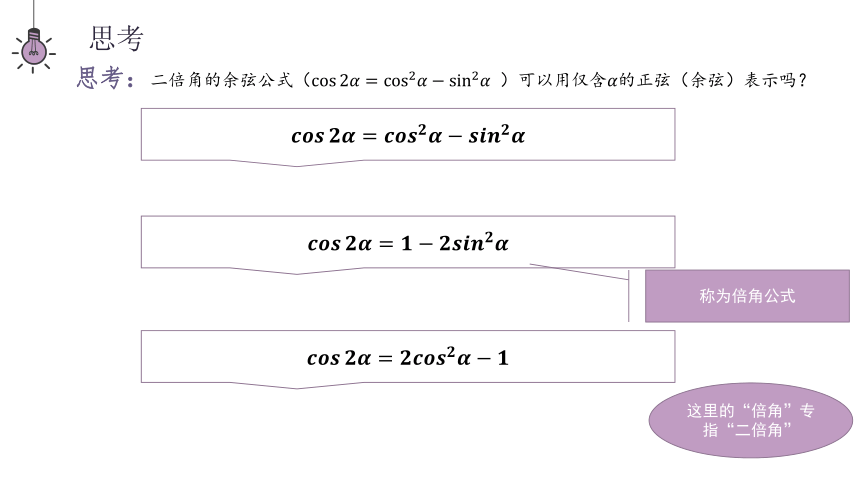
称为倍角公式
这里的“倍角”专指“二倍角”
思考:二倍角的余弦公式( )可以用仅含的正弦(余弦)表示吗?
思考
称为倍角公式
这里的“倍角”专指“二倍角”
例1.已知 , ,求,,的值.
解:由 ,得.(确定的象限以确定三角函数的正负)
又 ,
所以 .
于是
.
参考以上过程,独立将,求出.
例2.在△中,,,求(2A2B)的值.
2A+2B与A,B之间可以构成怎样的关系?
解法1:在 ABC中,由:
所以,
又
所以
于是
例2.在△中,,,求(2A2B)的值.
2A+2B与A,B之间可以构成怎样的关系?
解法2:在 ABC中,由:
所以,
又
所以
于是
1.已知.
变式训练
解:由:
所以,
2.已知.
利用倍角公式求值
解:由:
所以,
3.已知.
倍角公式的逆用
解:∵
∴ +6
∴
4..
(1); (2)
(3) (4)-1
倍角公式的逆用
解:(1)
课堂练习
PART 03
1.(1) ; (2) ; (3)
类型一:利用二倍角公式的简单应用
解:(1)原式
(2)原式
(3)原式
2.求sin6°·sin42°·sin66°·sin78°的值.
类型二:利用二倍角公式求非特殊角的三角函数值
解:方法一:原式
=
方法二:设所求为A,即A
则,
3.化简:.
类型三:利用二倍角公式化简三角函数式
解:方法一:原式
方法二:原式
4.求值:(1)已知;
(2)已知,求
类型四:二倍角公式在三角函数式给值求值题目中的应用
解:(1)
=
(2)
=
小结
PART 04
小结
谢谢
5.5.1 二倍角的正弦、余弦、正切公式
回顾和引入
PART 01
复习回顾
前面我们学习了:
由以上公式,你能推导出?
新课讲授
PART 02
探究:探究公式
自主探究展示
称为倍角公式
这里的“倍角”专指“二倍角”
思考:二倍角的余弦公式( )可以用仅含的正弦(余弦)表示吗?
思考
称为倍角公式
这里的“倍角”专指“二倍角”
例1.已知 , ,求,,的值.
解:由 ,得.(确定的象限以确定三角函数的正负)
又 ,
所以 .
于是
.
参考以上过程,独立将,求出.
例2.在△中,,,求(2A2B)的值.
2A+2B与A,B之间可以构成怎样的关系?
解法1:在 ABC中,由:
所以,
又
所以
于是
例2.在△中,,,求(2A2B)的值.
2A+2B与A,B之间可以构成怎样的关系?
解法2:在 ABC中,由:
所以,
又
所以
于是
1.已知.
变式训练
解:由:
所以,
2.已知.
利用倍角公式求值
解:由:
所以,
3.已知.
倍角公式的逆用
解:∵
∴ +6
∴
4..
(1); (2)
(3) (4)-1
倍角公式的逆用
解:(1)
课堂练习
PART 03
1.(1) ; (2) ; (3)
类型一:利用二倍角公式的简单应用
解:(1)原式
(2)原式
(3)原式
2.求sin6°·sin42°·sin66°·sin78°的值.
类型二:利用二倍角公式求非特殊角的三角函数值
解:方法一:原式
=
方法二:设所求为A,即A
则,
3.化简:.
类型三:利用二倍角公式化简三角函数式
解:方法一:原式
方法二:原式
4.求值:(1)已知;
(2)已知,求
类型四:二倍角公式在三角函数式给值求值题目中的应用
解:(1)
=
(2)
=
小结
PART 04
小结
谢谢
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
