人教版数学四年级下册10 总复习 四则运算的意义及其关系、运算定律课件(40张PPT)
文档属性
| 名称 | 人教版数学四年级下册10 总复习 四则运算的意义及其关系、运算定律课件(40张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览









文档简介
(共40张PPT)
人教版数学四年级(下)
第1课时 四则运算的意义及其关系、
运算定律
总复习
10
1.关注对四则运算的意义和各部分间的关系理解和运用。
2.掌握含有中括号的四则混合运算、运算定律和运算性质。
3.能熟练运用四则混合运算解决一些简单的实际问题。
学习目标
【重点】
能够灵活合理地选择乘法分配律、减法以及除法的运算性质进行简算。
【难点】
能熟练运用四则混合运算解决一些
简单的实际问题。
知识回顾
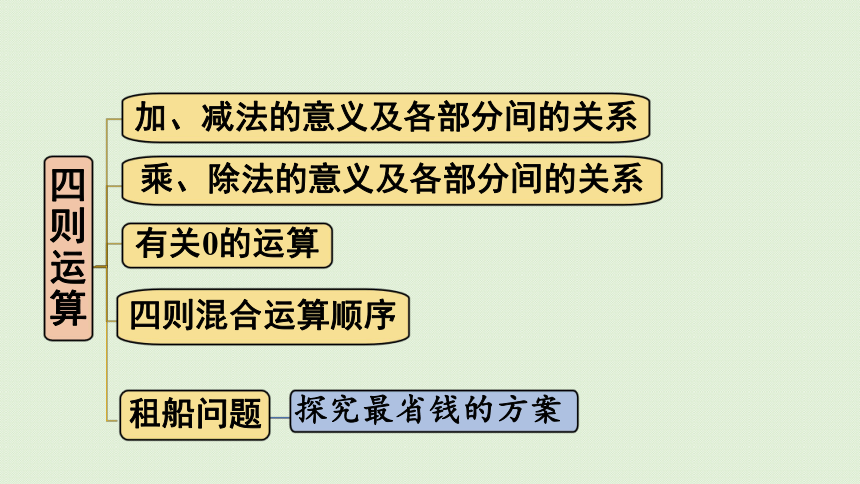
你还记得我们学过四则运算的哪些知识吗?
四则运算
加、减法的意义及各部分间的关系
乘、除法的意义及各部分间的关系
有关0的运算
四则混合运算顺序
租船问题
探究最省钱的方案
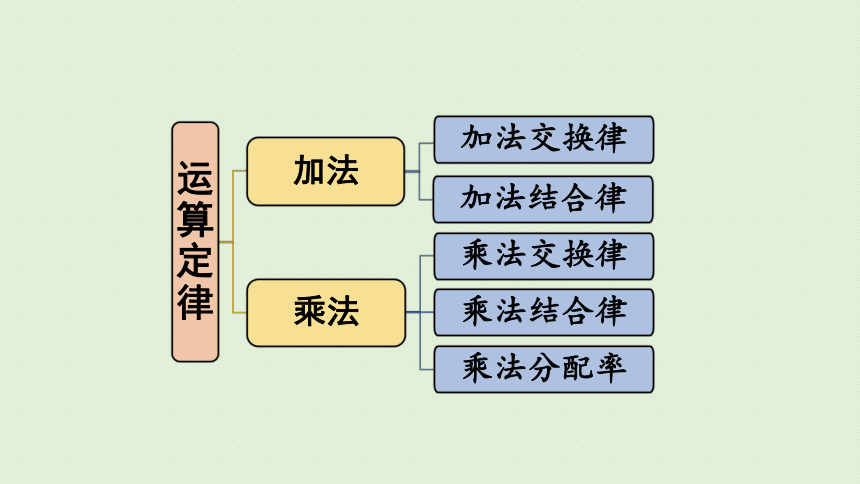
运算定律
加法
加法交换律
加法结合律
乘法
乘法交换律
乘法结合律
乘法分配率
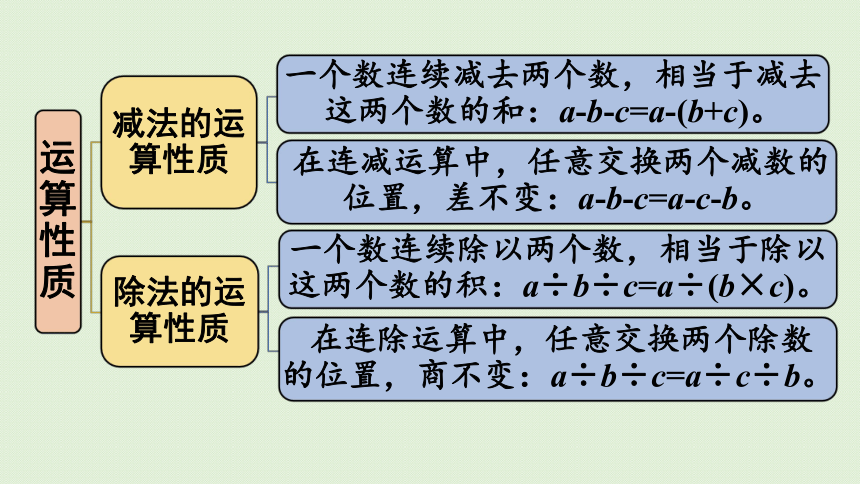
运算性质
减法的运算性质
一个数连续减去两个数,相当于减去这两个数的和:a-b-c=a-(b+c)。
在连减运算中,任意交换两个减数的位置,差不变:a-b-c=a-c-b。
除法的运算性质
一个数连续除以两个数,相当于除以这两个数的积:a÷b÷c=a÷(b×c)。
在连除运算中,任意交换两个除数的位置,商不变:a÷b÷c=a÷c÷b。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(1)根据第①个式子,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
(一)四则运算的意义和各部分之间的关系
重点解析
教材第109页第1(1)题
加法的意义和各部分的关系:
①意义:把两个数合并成一个数的运算,叫做
加法。
②各部分的关系:
316 + 59 = 375
加数+加数=和
(一)四则运算的意义和各部分之间的关系
和-加数=另一个加数
减法的意义和各部分的关系:
①意义:已知两个数的和与其中一个加数,求
另一个加数的运算,叫做减法。
②各部分的关系:
375 - 59 = 316
被减数-减数=差
(一)四则运算的意义和各部分之间的关系
被减数-差=减数
差+减数=被减数
加、减法的关系:减法是加法的逆运算。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(1)根据第①个式子,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
(一)四则运算的意义和各部分之间的关系
加法算式:59+316=375
减法算式:375-59=316或375-316=59
1.①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个式子,先说说乘法与除法的关系,再分别写出一个乘法算式和一个除法算式。
(一)四则运算的意义和各部分之间的关系
教材第109页第1(2)题
乘法的意义和各部分的关系:
①意义:求几个相同加数的和的简便运算,叫
做乘法。
②各部分的关系:
25 × 8 = 200
因数×因数=积
(一)四则运算的意义和各部分之间的关系
积÷因数=另一个因数
除法的意义和各部分的关系:
①意义:已知两个数的积与其中一个因数,求
另一个因数的运算,叫做除法。
②各部分的关系:
375 ÷ 3 = 125
被除数-除数=商
(一)四则运算的意义和各部分之间的关系
被除数÷商=除数
商×除数=被除数
乘除法的关系:除法是乘法的逆运算。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个式子,先说说乘法与除法的关系,再分别写出一个乘法算式和一个除法算式。
(一)四则运算的意义和各部分之间的关系
乘法算式:125×3=375或3×125=375
除法算式:375÷125=3
(二)有关0的运算
(1)一个数加上(或减去)0,还得原数。
(2)被减数等于减数,差是0。
(3)一个数和0相乘,仍得0。
(4)0除以一个非0的数,还得0。
1.①316+59=375 ②375÷3=125 ③125×16=200
(3)你会根据第①个和第②个算式列出一个综合算式吗?再根据第①个、第②个和第③个算式列出一个综合算式。
(三)四则混合运算
教材第109页第1(3)题
(三)四则混合运算
◎没有括号,只有加、减法或只有乘、除法,
按从左往右的顺序依次计算。
◎没有括号,既有乘、除法,又有加、减法,
要先算乘、除法,后算加、减法。
◎有括号的,要先算小括号里面的,再算中
括号里面的,最后算中括号外面的。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(3)你会根据第①个和第②个算式列出一个综合算式吗?再根据第①个、第②个和第③个算式列出一个综合算式。
(三)四则混合运算
375
316+59=375
316+59
÷3=125
( )
①②综合算式:(316+59)÷3=125
(316+59)÷3
125
×16=2000
①②③综合算式:(316+59)÷3×16=2000
1.①316+59=375 ②375÷3=125 ③125×16=200
(4)下面是小明和小兵的计算方法,说说他们各用了什么运算定律。
(四)运算定律和运算性质
教材第109页第1(4)题
小明
小兵
316+59
=316+(50+9)
=316+50+9
=366+9
=375
125×16
=125×(8×2)
=125×8×2
=1000×2
=2000
(四)运算定律和运算性质
运算定律:
◎加法交换律:a+b=b+a
◎加法结合律:(a+b)+c=a+(b+c)
◎乘法交换律:a×b=b×a
◎乘法结合律:(a×b)×c=a×(b×c)
◎乘法分配率:(a+b)×c=a×b+a×c)
(四)运算定律和运算性质
运算性质:
◎减法的运算性质:
①一个数连续减去两个数,相当于减去这两
个数的和:a-b-c=a-(b+c)。
②在连减运算中,任意交换两个减数的位置,
差不变:a-b-c=a-c-b。
(四)运算定律和运算性质
运算性质:
◎除法的运算性质:
①一个数连续除以两个数,相当于除以这两
个数的积:a÷b÷c=a÷(b×c)。
②在连除运算中,任意交换两个除数的位置,
商不变:a÷b÷c=a÷c÷b。
1.①316+59=375 ②375÷3=125 ③125×16=200
(4)下面是小明和小兵的计算方法,说说他们各用了什么运算定律。
(四)运算定律和运算性质
小明
小兵
316+59
=316+(50+9)
=316+50+9
=366+9
=375
125×16
=125×(8×2)
=125×8×2
=1000×2
=2000
加法结合律
乘法结合律
(五)租船问题
探究最省钱方案:
◎基本方法:先假设,再确定。
课堂练习
1.在括号中填入合适的数。
365-( )=185 ( )÷15=23
365-185=180
180
15×23=345
345
380-( )×8=140 ( )÷22=42……16
=
380-140=240
( )×8=240
240÷8=30
30
22×42+16=940
940
1.在括号中填入合适的数。
2.在 里填上“>”“<”或“=”。
(1)40×3×6 40×(3×6)
(2)360-120+40 360-(120+40)
(3)40+50+(12-8) (40+50)×(12-8)
(4)(150×8-480)÷24 150×8-480÷24
(a×b)×c=a×(b×c)
=
=360-120-40
>
=94
=360
<
=30
=1180
<
3.列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
456+328=
1000-275=
4 5 6
+ 3 2 8
4
1
8
7
验算
7 8 4
- 3 2 8
.
6
5
4
1 0 0 0
- 2 7 5
.
5
2
7
.
.
784
验算
7 2 5
+ 2 7 5
0
1
0
0
1
1
725
3.列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
32×125=
324÷12=
3 2
× 1 2 5
0
1
6
1
4
6
2
3
0
1
0
1
0
4
验算
4 0 0 0
3 2
1
3 2
8
0
2
6 4
1 6
0
5
1 6 0
0
27
3 2 4
1 2
2
2 4
8
4
7
8 4
0
验算
1 2
× 2 7
4
1
8
4
2
4
1
2
3
4000
4.先说一说运算顺序,再进行计算。
125+25×6
(135+75)÷(14×5)
=125+150
=275
=210+70
=3
乘法 加法
加法、乘法 加法
100÷[80÷(68-48)]
206+108÷(61-49)
=100÷[80÷20]
=100÷4
=25
=206+108÷12
=206+9
=215
减法 除法 除法
减法 除法 加法
4.先说一说运算顺序,再进行计算。
5.怎样简便怎样算。
837+261+163
476-129-71
287×36-87×36
=837+163+261
=1000+261
=1261
=476-(129+71)
=476-200
=276
=36×(287-87)
=36×200
=7200
加法交换律
减法的性质
乘法分配律
5.怎样简便怎样算。
56×125
125×8÷125×8
63000÷25÷4
=7×(8×125)
=7×1000
=7000
=125÷125×8×8
=1×8×8
=64
=63000÷(25×4)
=63000÷100
=630
乘法结合律
除法的运算性质
6.妈妈带了500元去超市,买了一条裤子,用去
了148元,又买了一件羊毛衫,用去了152元,
还剩下多少钱?(用两种方法解答)
方法一:
500-148-152
=352-152
=200(元)
方法二:
500-148-152
=500-(148+152)
=500-300
=200(元)
答:还剩下200元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
1000÷40 =25(元)
650÷25=26(元)
25<26 租大车便宜。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
方案一:全租大车。
115÷40 =2(辆)……35(人)
2+1=3(元)
3×1000=3000(元)
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
方案二:尽量租大车,剩余人乘小车。
115÷40 =2(辆)……35(人)
35÷25=1(辆)……10(人)
可以租2辆大车和2辆小车。
租金:1000×2+650×2=3300(元)
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
方案三:调整大车、小车数量,使空座最少。
115-40 =75(人)
75÷25=3(辆)
可以租1辆大车和3辆小车
租金:
1000+650×3=2950(元)
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
2950<3000<3300
答:租1辆大车和3辆小车最省钱。
人教版数学四年级(下)
第1课时 四则运算的意义及其关系、
运算定律
总复习
10
1.关注对四则运算的意义和各部分间的关系理解和运用。
2.掌握含有中括号的四则混合运算、运算定律和运算性质。
3.能熟练运用四则混合运算解决一些简单的实际问题。
学习目标
【重点】
能够灵活合理地选择乘法分配律、减法以及除法的运算性质进行简算。
【难点】
能熟练运用四则混合运算解决一些
简单的实际问题。
知识回顾
你还记得我们学过四则运算的哪些知识吗?
四则运算
加、减法的意义及各部分间的关系
乘、除法的意义及各部分间的关系
有关0的运算
四则混合运算顺序
租船问题
探究最省钱的方案
运算定律
加法
加法交换律
加法结合律
乘法
乘法交换律
乘法结合律
乘法分配率
运算性质
减法的运算性质
一个数连续减去两个数,相当于减去这两个数的和:a-b-c=a-(b+c)。
在连减运算中,任意交换两个减数的位置,差不变:a-b-c=a-c-b。
除法的运算性质
一个数连续除以两个数,相当于除以这两个数的积:a÷b÷c=a÷(b×c)。
在连除运算中,任意交换两个除数的位置,商不变:a÷b÷c=a÷c÷b。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(1)根据第①个式子,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
(一)四则运算的意义和各部分之间的关系
重点解析
教材第109页第1(1)题
加法的意义和各部分的关系:
①意义:把两个数合并成一个数的运算,叫做
加法。
②各部分的关系:
316 + 59 = 375
加数+加数=和
(一)四则运算的意义和各部分之间的关系
和-加数=另一个加数
减法的意义和各部分的关系:
①意义:已知两个数的和与其中一个加数,求
另一个加数的运算,叫做减法。
②各部分的关系:
375 - 59 = 316
被减数-减数=差
(一)四则运算的意义和各部分之间的关系
被减数-差=减数
差+减数=被减数
加、减法的关系:减法是加法的逆运算。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(1)根据第①个式子,先说说加法与减法的关系,再分别写出一个加法算式和一个减法算式。
(一)四则运算的意义和各部分之间的关系
加法算式:59+316=375
减法算式:375-59=316或375-316=59
1.①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个式子,先说说乘法与除法的关系,再分别写出一个乘法算式和一个除法算式。
(一)四则运算的意义和各部分之间的关系
教材第109页第1(2)题
乘法的意义和各部分的关系:
①意义:求几个相同加数的和的简便运算,叫
做乘法。
②各部分的关系:
25 × 8 = 200
因数×因数=积
(一)四则运算的意义和各部分之间的关系
积÷因数=另一个因数
除法的意义和各部分的关系:
①意义:已知两个数的积与其中一个因数,求
另一个因数的运算,叫做除法。
②各部分的关系:
375 ÷ 3 = 125
被除数-除数=商
(一)四则运算的意义和各部分之间的关系
被除数÷商=除数
商×除数=被除数
乘除法的关系:除法是乘法的逆运算。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(2)根据第②个式子,先说说乘法与除法的关系,再分别写出一个乘法算式和一个除法算式。
(一)四则运算的意义和各部分之间的关系
乘法算式:125×3=375或3×125=375
除法算式:375÷125=3
(二)有关0的运算
(1)一个数加上(或减去)0,还得原数。
(2)被减数等于减数,差是0。
(3)一个数和0相乘,仍得0。
(4)0除以一个非0的数,还得0。
1.①316+59=375 ②375÷3=125 ③125×16=200
(3)你会根据第①个和第②个算式列出一个综合算式吗?再根据第①个、第②个和第③个算式列出一个综合算式。
(三)四则混合运算
教材第109页第1(3)题
(三)四则混合运算
◎没有括号,只有加、减法或只有乘、除法,
按从左往右的顺序依次计算。
◎没有括号,既有乘、除法,又有加、减法,
要先算乘、除法,后算加、减法。
◎有括号的,要先算小括号里面的,再算中
括号里面的,最后算中括号外面的。
1.①316+59=375 ②375÷3=125 ③125×16=2000
(3)你会根据第①个和第②个算式列出一个综合算式吗?再根据第①个、第②个和第③个算式列出一个综合算式。
(三)四则混合运算
375
316+59=375
316+59
÷3=125
( )
①②综合算式:(316+59)÷3=125
(316+59)÷3
125
×16=2000
①②③综合算式:(316+59)÷3×16=2000
1.①316+59=375 ②375÷3=125 ③125×16=200
(4)下面是小明和小兵的计算方法,说说他们各用了什么运算定律。
(四)运算定律和运算性质
教材第109页第1(4)题
小明
小兵
316+59
=316+(50+9)
=316+50+9
=366+9
=375
125×16
=125×(8×2)
=125×8×2
=1000×2
=2000
(四)运算定律和运算性质
运算定律:
◎加法交换律:a+b=b+a
◎加法结合律:(a+b)+c=a+(b+c)
◎乘法交换律:a×b=b×a
◎乘法结合律:(a×b)×c=a×(b×c)
◎乘法分配率:(a+b)×c=a×b+a×c)
(四)运算定律和运算性质
运算性质:
◎减法的运算性质:
①一个数连续减去两个数,相当于减去这两
个数的和:a-b-c=a-(b+c)。
②在连减运算中,任意交换两个减数的位置,
差不变:a-b-c=a-c-b。
(四)运算定律和运算性质
运算性质:
◎除法的运算性质:
①一个数连续除以两个数,相当于除以这两
个数的积:a÷b÷c=a÷(b×c)。
②在连除运算中,任意交换两个除数的位置,
商不变:a÷b÷c=a÷c÷b。
1.①316+59=375 ②375÷3=125 ③125×16=200
(4)下面是小明和小兵的计算方法,说说他们各用了什么运算定律。
(四)运算定律和运算性质
小明
小兵
316+59
=316+(50+9)
=316+50+9
=366+9
=375
125×16
=125×(8×2)
=125×8×2
=1000×2
=2000
加法结合律
乘法结合律
(五)租船问题
探究最省钱方案:
◎基本方法:先假设,再确定。
课堂练习
1.在括号中填入合适的数。
365-( )=185 ( )÷15=23
365-185=180
180
15×23=345
345
380-( )×8=140 ( )÷22=42……16
=
380-140=240
( )×8=240
240÷8=30
30
22×42+16=940
940
1.在括号中填入合适的数。
2.在 里填上“>”“<”或“=”。
(1)40×3×6 40×(3×6)
(2)360-120+40 360-(120+40)
(3)40+50+(12-8) (40+50)×(12-8)
(4)(150×8-480)÷24 150×8-480÷24
(a×b)×c=a×(b×c)
=
=360-120-40
>
=94
=360
<
=30
=1180
<
3.列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
456+328=
1000-275=
4 5 6
+ 3 2 8
4
1
8
7
验算
7 8 4
- 3 2 8
.
6
5
4
1 0 0 0
- 2 7 5
.
5
2
7
.
.
784
验算
7 2 5
+ 2 7 5
0
1
0
0
1
1
725
3.列竖式计算并根据加、减法或乘、除法各部分之间的关系进行验算。
32×125=
324÷12=
3 2
× 1 2 5
0
1
6
1
4
6
2
3
0
1
0
1
0
4
验算
4 0 0 0
3 2
1
3 2
8
0
2
6 4
1 6
0
5
1 6 0
0
27
3 2 4
1 2
2
2 4
8
4
7
8 4
0
验算
1 2
× 2 7
4
1
8
4
2
4
1
2
3
4000
4.先说一说运算顺序,再进行计算。
125+25×6
(135+75)÷(14×5)
=125+150
=275
=210+70
=3
乘法 加法
加法、乘法 加法
100÷[80÷(68-48)]
206+108÷(61-49)
=100÷[80÷20]
=100÷4
=25
=206+108÷12
=206+9
=215
减法 除法 除法
减法 除法 加法
4.先说一说运算顺序,再进行计算。
5.怎样简便怎样算。
837+261+163
476-129-71
287×36-87×36
=837+163+261
=1000+261
=1261
=476-(129+71)
=476-200
=276
=36×(287-87)
=36×200
=7200
加法交换律
减法的性质
乘法分配律
5.怎样简便怎样算。
56×125
125×8÷125×8
63000÷25÷4
=7×(8×125)
=7×1000
=7000
=125÷125×8×8
=1×8×8
=64
=63000÷(25×4)
=63000÷100
=630
乘法结合律
除法的运算性质
6.妈妈带了500元去超市,买了一条裤子,用去
了148元,又买了一件羊毛衫,用去了152元,
还剩下多少钱?(用两种方法解答)
方法一:
500-148-152
=352-152
=200(元)
方法二:
500-148-152
=500-(148+152)
=500-300
=200(元)
答:还剩下200元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
1000÷40 =25(元)
650÷25=26(元)
25<26 租大车便宜。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
方案一:全租大车。
115÷40 =2(辆)……35(人)
2+1=3(元)
3×1000=3000(元)
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
方案二:尽量租大车,剩余人乘小车。
115÷40 =2(辆)……35(人)
35÷25=1(辆)……10(人)
可以租2辆大车和2辆小车。
租金:1000×2+650×2=3300(元)
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
方案三:调整大车、小车数量,使空座最少。
115-40 =75(人)
75÷25=3(辆)
可以租1辆大车和3辆小车
租金:
1000+650×3=2950(元)
7. 育英小学115人准备去博物院观看华夏古乐
团演出,有两种可以租用的车型,怎样租车
最省钱呢?请你设计一个租车方案。
大车:限乘客40人,每辆租金1000元。
小车:限乘客25人,每辆租金650元。
2950<3000<3300
答:租1辆大车和3辆小车最省钱。
