【人教版】数学九年级下册 27.2.1第2课时-相似三角形的判定(1)习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 27.2.1第2课时-相似三角形的判定(1)习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 676.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览




文档简介
(共15张PPT)
下页
上页
N课前预习\习新知
相似三角形的判定定理:
1.三边成比例的两个三角形相似
2.两边成比例且夹角相等的两个三角
形相似
当堂训练巩国基
知织点1三边成比例的两个三角形相似
1.已知△ABC的三边长分别为2,5,6,若要使
△DEF∽△ABC,则△DEF的三边长可以是
(B)
A.3,6,7
B.6,15,18
0
2.如图,小正方形的边长均为1,则下列图中的
三角形(阴影部分)与△ABC相似的是(B)
A
B
C
D
3.已知△ABC的三边长分别是6cm,7.5cm,
9cm,△DEF的一边长为4cm.若△DEF与
△ABC相似,则△DEF的另外两边长可能为
(C)
A. 2 cm,3 cm
B. 4 cm.5 cm
C.5 cm. 6 cm
D. 6 cm. 7 cm
4.△ABC的三边长分别为3,3,15,△ABC'的
两边长分别为1和√5,当△AB'C的第三边
长为3时,△ABC与△ABC′相似
知织点2两边成比例且夹角相等的两个三角
形相似
5.如图,在△ABC与△ADE中,∠BAD=
∠CAE,要使△ABC∽△AED,还需满足下列
条件中的
(A)
A. AC_AB
AC BC
AD AE
AD DE
AC AB
D
AC BC
AD DE
AD AE
E
D
B
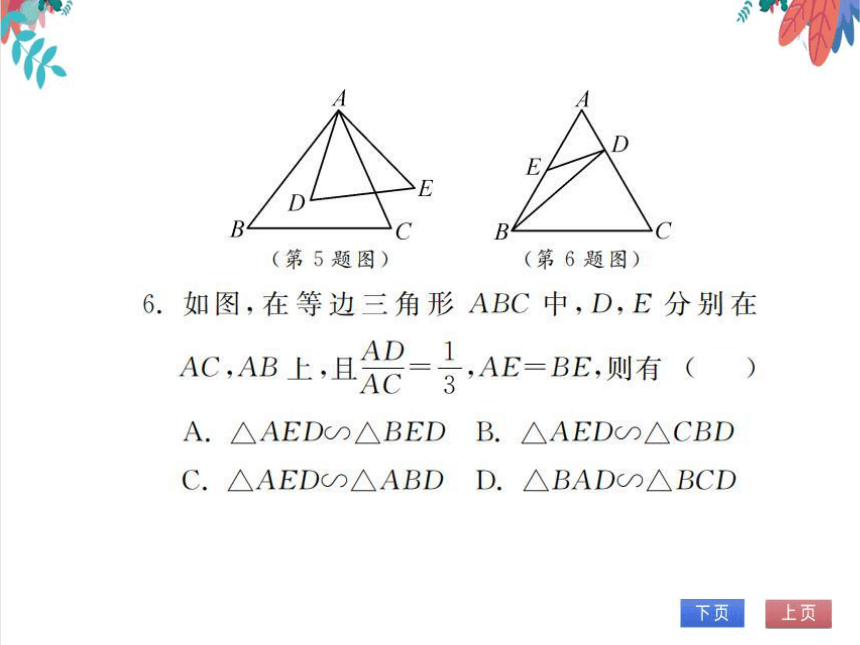
(第5题图)
(第6题图)
6.如图,在等边三角形ABC中,D,E分别在
AD 1
AC,AB上,且
ac 3
,AE=BE,则有(B)
A.△AED∽△BEDB.△AED∽△CBD
C.△AED∽△ABDD.△BAD∽△BCD
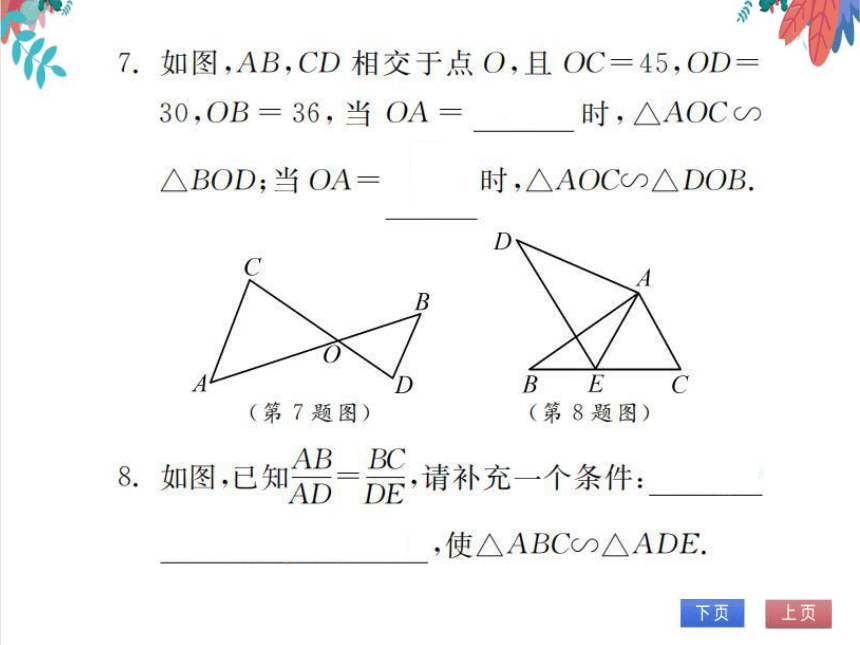
7.如图,AB,CD相交于点O,且OC=45,OD
30,OB=36,当OA
54时,△AOC∽
△BOD;当OA=2时,△AOCO△DOB
D
(第7题图)
(第8题图)
8.如图,已知AD=DE,请补充一个条件:∠B
∠D(答案不唯一),使△ABC∽△ADE
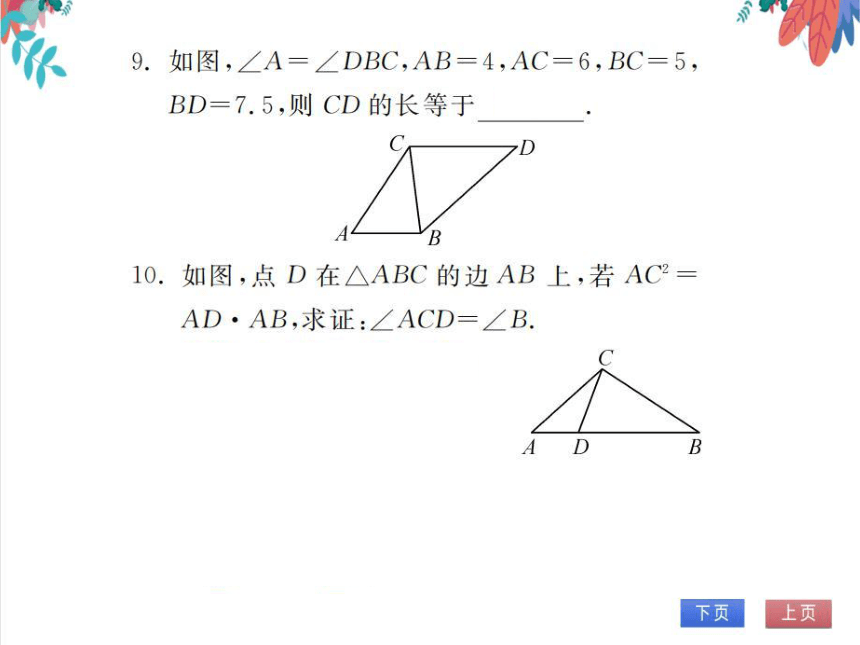
9.如图,∠A=∠DBC,AB=4,AC=6,BC=5,
BD=7.5,则CD的长等于6.25
D
10.如图,点D在△ABC的边AB上,若AC
AD·AB,求证:∠ACD=∠B
证明:∵AC=AD·AB,
AC AB
AD AC
B
又∵∠A=∠A,
∴△ACD∽△ABC
∴∠ACD=∠B
课后作业全面提升
1.如图,在大小为4×4的正方形网格中各有
个三角形,其中是相似三角形的是
(C)
A.①和②
B.②和③
C.①和③
D.②和④
2.如图,在等腰三角形ABC中,AB=AC,D是
CB的延长线上一点,E是BC的延长线上
点,且AB2=DB·CE,若∠BAC=40°,则
∠DAE的度数是
(D)
A.100°B.120°C.130°D.110°
下页
上页
N课前预习\习新知
相似三角形的判定定理:
1.三边成比例的两个三角形相似
2.两边成比例且夹角相等的两个三角
形相似
当堂训练巩国基
知织点1三边成比例的两个三角形相似
1.已知△ABC的三边长分别为2,5,6,若要使
△DEF∽△ABC,则△DEF的三边长可以是
(B)
A.3,6,7
B.6,15,18
0
2.如图,小正方形的边长均为1,则下列图中的
三角形(阴影部分)与△ABC相似的是(B)
A
B
C
D
3.已知△ABC的三边长分别是6cm,7.5cm,
9cm,△DEF的一边长为4cm.若△DEF与
△ABC相似,则△DEF的另外两边长可能为
(C)
A. 2 cm,3 cm
B. 4 cm.5 cm
C.5 cm. 6 cm
D. 6 cm. 7 cm
4.△ABC的三边长分别为3,3,15,△ABC'的
两边长分别为1和√5,当△AB'C的第三边
长为3时,△ABC与△ABC′相似
知织点2两边成比例且夹角相等的两个三角
形相似
5.如图,在△ABC与△ADE中,∠BAD=
∠CAE,要使△ABC∽△AED,还需满足下列
条件中的
(A)
A. AC_AB
AC BC
AD AE
AD DE
AC AB
D
AC BC
AD DE
AD AE
E
D
B
(第5题图)
(第6题图)
6.如图,在等边三角形ABC中,D,E分别在
AD 1
AC,AB上,且
ac 3
,AE=BE,则有(B)
A.△AED∽△BEDB.△AED∽△CBD
C.△AED∽△ABDD.△BAD∽△BCD
7.如图,AB,CD相交于点O,且OC=45,OD
30,OB=36,当OA
54时,△AOC∽
△BOD;当OA=2时,△AOCO△DOB
D
(第7题图)
(第8题图)
8.如图,已知AD=DE,请补充一个条件:∠B
∠D(答案不唯一),使△ABC∽△ADE
9.如图,∠A=∠DBC,AB=4,AC=6,BC=5,
BD=7.5,则CD的长等于6.25
D
10.如图,点D在△ABC的边AB上,若AC
AD·AB,求证:∠ACD=∠B
证明:∵AC=AD·AB,
AC AB
AD AC
B
又∵∠A=∠A,
∴△ACD∽△ABC
∴∠ACD=∠B
课后作业全面提升
1.如图,在大小为4×4的正方形网格中各有
个三角形,其中是相似三角形的是
(C)
A.①和②
B.②和③
C.①和③
D.②和④
2.如图,在等腰三角形ABC中,AB=AC,D是
CB的延长线上一点,E是BC的延长线上
点,且AB2=DB·CE,若∠BAC=40°,则
∠DAE的度数是
(D)
A.100°B.120°C.130°D.110°
