【人教版】数学九年级下册 27.2.1第3课时-相似三角形的判定(2)习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 27.2.1第3课时-相似三角形的判定(2)习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 694.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览






文档简介
(共18张PPT)
下页
上页
Ⅲ课前预习
1.相似三角形的判定定理:两角分别相等的
两个三角形相似
2.两个直角三角形相似的判定方法:
(1)有一个锐角相等的两个直角三角形相似;
(2)有两组直角边成比例的两个直角三角形
相似;
(3)斜边与一直角边对应成比例的两个直角三
角形相似
当堂训练\巩基
知织点1两角分别相等的两个三角形相似
1.下列各条件中,不能判定△ABC与△A'B'C′
相似的是
(C)
A.∠A=∠A,∠B=∠B
B.∠C=∠C=90°,∠A=35°,∠B=55°
C.∠A=∠B,∠A′=∠B
D.∠A+∠B=∠A+∠B,∠A-∠B
∠A-∠B
2.已知等腰△ABC的底角为75°,则下列三角形
定与△ABC相似的是
(A)
A.顶角为30°的等腰三角形
B.顶角为40°的等腰三角形
C.等边三角形
D.顶角为75°的等腰三角形
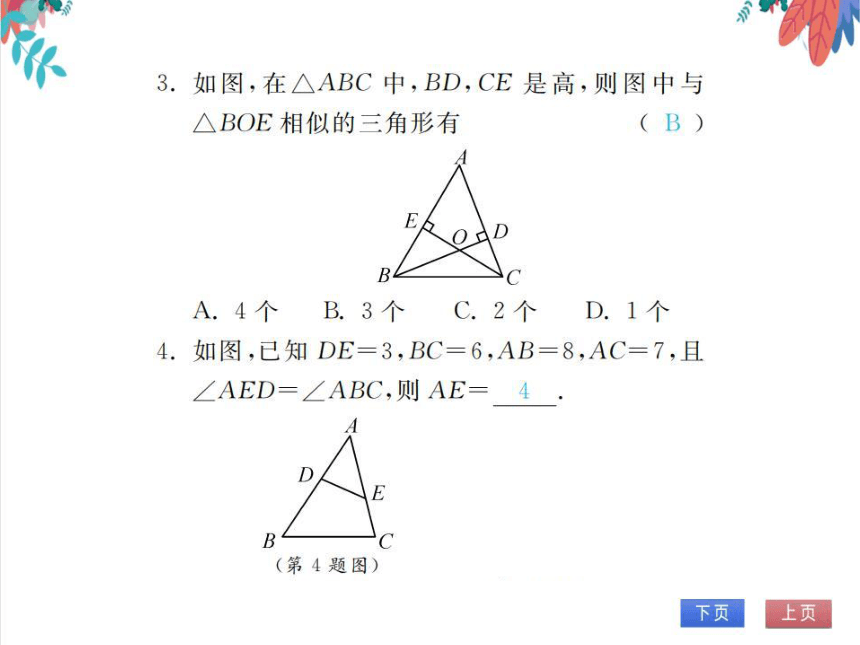
3.如图,在△ABC中,BD,CE是高,则图中与
△BOE相似的三角形有
( B
D
B
A.4个B.3个C.2个D.1个
4.如图,已知DE=3,BC=6,AB=8,AC=7,且
∠AED=∠ABC,则AE=4
E
B
B D
(第4题图)
(第5题图)
知识点2直角三角形相似的判定
6.如图,在Rt△ABC中,∠C=90°,D是BC上
点,已知CD=1,AD=√5,若要证明
Rt△ADC∽Rt△BAC,则AB的长应为(D)
A.2
D.2√5
(第6题图)
(第7题图)
7.如图,AD∥BC,AD⊥CD,∠BAC=90°,已知
AD=4,BC=9,则AC=6
8.如图,正方形ABCD的边长为2,BE=CE,
MN=1,线段MN的端点分别在CD,AD上
滑动,当DM=
或
时,△ABE与以
D,M,N为顶点的三角形相似
BE O
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB
于点D.求证
(1)CD2=AD·BD;
(2)AC2=AD·AB
证明:(1)如图,
∴CD⊥AB,
∴∠1=∠2=90°
∵∠ACB=90
A
∴∠A+∠3=∠3+∠4=90°
∴∠A=∠4
△ADC△CDB.∴AD=CD
CD BD
∴CD2=AD·BD.
课后作业
全面提升
1.如图,在△ABC中,D,E两点分别在BC,AC
上,且AD平分∠BAC,若∠ABE=∠C,BE
与AD相交于点F,则图中相似三角形的对数
是
A.1
B.2
D.4
E
F
B
(第1题图)
(第2题图)
2.如图,∠1=∠2=∠3,则下列结论不正确的是
(C)
A.△DEC∽△ABCB.△ADE∽△BEA
C.△ACE∽△BEAD.△ACE∽△BCA
下页
上页
Ⅲ课前预习
1.相似三角形的判定定理:两角分别相等的
两个三角形相似
2.两个直角三角形相似的判定方法:
(1)有一个锐角相等的两个直角三角形相似;
(2)有两组直角边成比例的两个直角三角形
相似;
(3)斜边与一直角边对应成比例的两个直角三
角形相似
当堂训练\巩基
知织点1两角分别相等的两个三角形相似
1.下列各条件中,不能判定△ABC与△A'B'C′
相似的是
(C)
A.∠A=∠A,∠B=∠B
B.∠C=∠C=90°,∠A=35°,∠B=55°
C.∠A=∠B,∠A′=∠B
D.∠A+∠B=∠A+∠B,∠A-∠B
∠A-∠B
2.已知等腰△ABC的底角为75°,则下列三角形
定与△ABC相似的是
(A)
A.顶角为30°的等腰三角形
B.顶角为40°的等腰三角形
C.等边三角形
D.顶角为75°的等腰三角形
3.如图,在△ABC中,BD,CE是高,则图中与
△BOE相似的三角形有
( B
D
B
A.4个B.3个C.2个D.1个
4.如图,已知DE=3,BC=6,AB=8,AC=7,且
∠AED=∠ABC,则AE=4
E
B
B D
(第4题图)
(第5题图)
知识点2直角三角形相似的判定
6.如图,在Rt△ABC中,∠C=90°,D是BC上
点,已知CD=1,AD=√5,若要证明
Rt△ADC∽Rt△BAC,则AB的长应为(D)
A.2
D.2√5
(第6题图)
(第7题图)
7.如图,AD∥BC,AD⊥CD,∠BAC=90°,已知
AD=4,BC=9,则AC=6
8.如图,正方形ABCD的边长为2,BE=CE,
MN=1,线段MN的端点分别在CD,AD上
滑动,当DM=
或
时,△ABE与以
D,M,N为顶点的三角形相似
BE O
9.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB
于点D.求证
(1)CD2=AD·BD;
(2)AC2=AD·AB
证明:(1)如图,
∴CD⊥AB,
∴∠1=∠2=90°
∵∠ACB=90
A
∴∠A+∠3=∠3+∠4=90°
∴∠A=∠4
△ADC△CDB.∴AD=CD
CD BD
∴CD2=AD·BD.
课后作业
全面提升
1.如图,在△ABC中,D,E两点分别在BC,AC
上,且AD平分∠BAC,若∠ABE=∠C,BE
与AD相交于点F,则图中相似三角形的对数
是
A.1
B.2
D.4
E
F
B
(第1题图)
(第2题图)
2.如图,∠1=∠2=∠3,则下列结论不正确的是
(C)
A.△DEC∽△ABCB.△ADE∽△BEA
C.△ACE∽△BEAD.△ACE∽△BCA
