【人教版】数学九年级下册 27.2.2相似三角形的性质 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 27.2.2相似三角形的性质 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 715.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览






文档简介
(共16张PPT)
下页
上页
课前预习习新如
1.相似三角形对应高的比等于相似比,对应
角平分线的比等于相似比,对应中线的比
等于相似比
2.相似三角形周长的比等于相似比
3.相似三角形面积的比等于相似比的平方
当堂训练巩基础
知识点1相似三角形对应线段的比等于相似比
1.(兰州改编)已知△ABC∽△ABC,AB=8,
A'B′=6,则△ABC与△A'BC对应高的比是
(B)
A.2
B.
C.3
D
16
2.已知△ABC∽△AB'C",相似比为3:4,AD
AD分别是边BC,BC上的中线,则AD:AD
3:4.若AD=9cm,则AD′=12cm
3.已知△ABC∽△A'BC′,AB=3cm,A'B
8cm,AE是△ABC的角平分线,且AE
2.1cm,则△ABC'中对应角平分线A'E'的
长是5.6cm
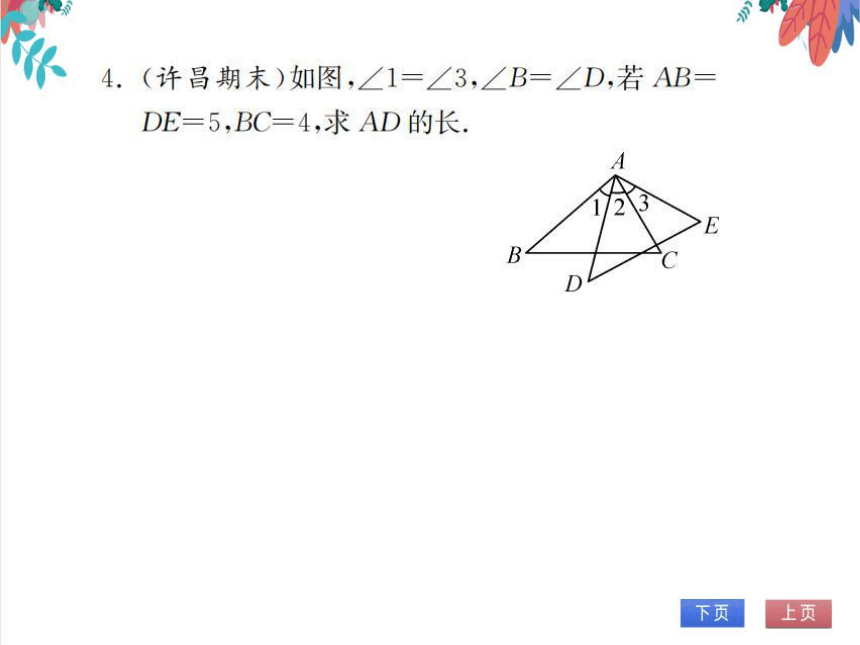
4.(许昌期末)如图,∠1=∠3,∠B=∠D,若AB
DE=5,BC=4,求AD的长
解:∵∠1=∠3
∴∠1+∠2=∠3+∠2
E
即∠BAC=∠DAE
B
∵∠B=∠D
∴△ABC∽△ADE
AB BC
AD DE
又∵AB=DE=5,BC=4
∴AD=25
AD 5
6.已知△ABC∽△DEF,若AB=3,AC=4
BC=5,△DEF的最长边长为15,则△DEF
的周长为36
7.(武汉模拟)若△ABC∽△DEF,且相似比是
2:3,它们的周长之和为40,则△ABC的周长
是16
知识点3相似三角形面积的比等于相似比的
平方
8.(玉林)两三角形的相似比是2:3,则其面积之
比是
(C)
A.√2:3B.2:
C.4:9D.8:27
9.如图,在梯形ABCD中,AB∥CD,△DCE的
面积与△DCB的面积之比为1:3,则△DCE
的面积与△BEA的面积之比为
(B)
A.1:3B.1:4C.1:5D.1:9
E
B
C
(第9题图)
(第10题图)
10.(教材P43习题T12变式)如图,平行于BC
的直线DE把△ABC分成面积相等的两部
BD
分,则的值为
(C)
2
B
1D.√2+1
11.已知△ABCC△DEF,相似比为2,且△ABC
的面积为16,则△DEF的面积为4
2.(荆门改编)如图,四边形ABCD为平行四边
形,E,F为CD边的两个三等分点,连接AF,
BE交于点G,若S△ABG=12,求S△EFG
解:∵E,F为CD边的两
DE F C
个三等分点,
∴EF=CD.
∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴EF=1
AB,△EFG∽△BAG
3
∴≌△EFG
EF\2Z
AB
°△EFG
下页
上页
课前预习习新如
1.相似三角形对应高的比等于相似比,对应
角平分线的比等于相似比,对应中线的比
等于相似比
2.相似三角形周长的比等于相似比
3.相似三角形面积的比等于相似比的平方
当堂训练巩基础
知识点1相似三角形对应线段的比等于相似比
1.(兰州改编)已知△ABC∽△ABC,AB=8,
A'B′=6,则△ABC与△A'BC对应高的比是
(B)
A.2
B.
C.3
D
16
2.已知△ABC∽△AB'C",相似比为3:4,AD
AD分别是边BC,BC上的中线,则AD:AD
3:4.若AD=9cm,则AD′=12cm
3.已知△ABC∽△A'BC′,AB=3cm,A'B
8cm,AE是△ABC的角平分线,且AE
2.1cm,则△ABC'中对应角平分线A'E'的
长是5.6cm
4.(许昌期末)如图,∠1=∠3,∠B=∠D,若AB
DE=5,BC=4,求AD的长
解:∵∠1=∠3
∴∠1+∠2=∠3+∠2
E
即∠BAC=∠DAE
B
∵∠B=∠D
∴△ABC∽△ADE
AB BC
AD DE
又∵AB=DE=5,BC=4
∴AD=25
AD 5
6.已知△ABC∽△DEF,若AB=3,AC=4
BC=5,△DEF的最长边长为15,则△DEF
的周长为36
7.(武汉模拟)若△ABC∽△DEF,且相似比是
2:3,它们的周长之和为40,则△ABC的周长
是16
知识点3相似三角形面积的比等于相似比的
平方
8.(玉林)两三角形的相似比是2:3,则其面积之
比是
(C)
A.√2:3B.2:
C.4:9D.8:27
9.如图,在梯形ABCD中,AB∥CD,△DCE的
面积与△DCB的面积之比为1:3,则△DCE
的面积与△BEA的面积之比为
(B)
A.1:3B.1:4C.1:5D.1:9
E
B
C
(第9题图)
(第10题图)
10.(教材P43习题T12变式)如图,平行于BC
的直线DE把△ABC分成面积相等的两部
BD
分,则的值为
(C)
2
B
1D.√2+1
11.已知△ABCC△DEF,相似比为2,且△ABC
的面积为16,则△DEF的面积为4
2.(荆门改编)如图,四边形ABCD为平行四边
形,E,F为CD边的两个三等分点,连接AF,
BE交于点G,若S△ABG=12,求S△EFG
解:∵E,F为CD边的两
DE F C
个三等分点,
∴EF=CD.
∵四边形ABCD为平行四边形
∴AB∥CD,AB=CD
∴EF=1
AB,△EFG∽△BAG
3
∴≌△EFG
EF\2Z
AB
°△EFG
