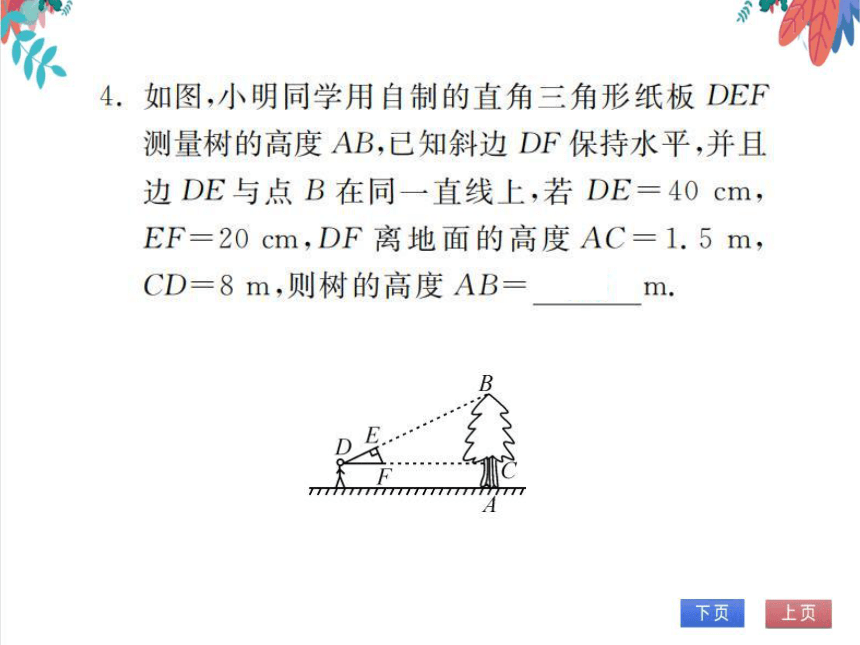
【人教版】数学九年级下册 27.2.3相似三角形应用举例 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 27.2.3相似三角形应用举例 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 849.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览





文档简介
(共16张PPT)
下页
上页
N课前预习
预习新知
利用三角形相似解决实际问题的一般步骤:(1)根据
题意画出示意图;(2)将题目中的已知量或已知
关系转化为示意图中的已知线段、已知角或它们
之间的关系;(3)利用相似三角形建立线段之间
的关系,求出未知量;(4)写出答案
知识点1利用相似测量物体的高度
1.如图,小明在地面上放了一个平面镜,选择合
适的位置,刚好在平面镜中看到旗杆的顶部
此时小明与平面镜的水平距离为2m,旗杆底
部与平面镜的水平距离为16m,若小明的眼睛与
地面的距离为1.5m,则旗杆的高度为(B
m B 12 m C.9 m D
16
(第1题图)
第2题图)
2.(天水)如图,某校数学兴趣小组利用标杆BE
测量建筑物的高度,已知标杆BE高1.5m,测
得AB=1.2m,BC=12.8m,则建筑物CD的
高是
(A)
A.17.5mB.17mC.16.5mD.18m
3.(绍兴)学校门口的栏杆如图所示,栏杆从水平
位置BD绕O点旋转到AC位置,已知AB⊥
BD,CD⊥BD,垂足分别为B,D,AO=4m,
AB=1.6m,CO=1m,则栏杆C端应下降的
垂直距离CD为0.4m
(第3题图
(第4题图
5.如图,有两堵墙AB,CD,AB墙高2m,两墙之
间的距离BC为8m,小明将一架木梯放在距
B点3m的E处靠向墙AB时,木梯有很多露
出墙外.将木梯绕点E旋转90°靠向墙CD时,
木梯刚好达到墙的顶点D,求墙CD的高
解:由题意可知∠B=∠C
D
90°,∠AED=90°,BE=3m,
:.CE-BC-BE==(m),B E
∠BAE+∠AEB=90°,∠AEB+∠DEC
90.∴∠BAE=∠DEC.∴△ABE∽△ECD
AB BE 2 3
EC DC
解得DC=7.5
因此墙CD的高为7.5m
知织点2利用相似测量物体的宽度
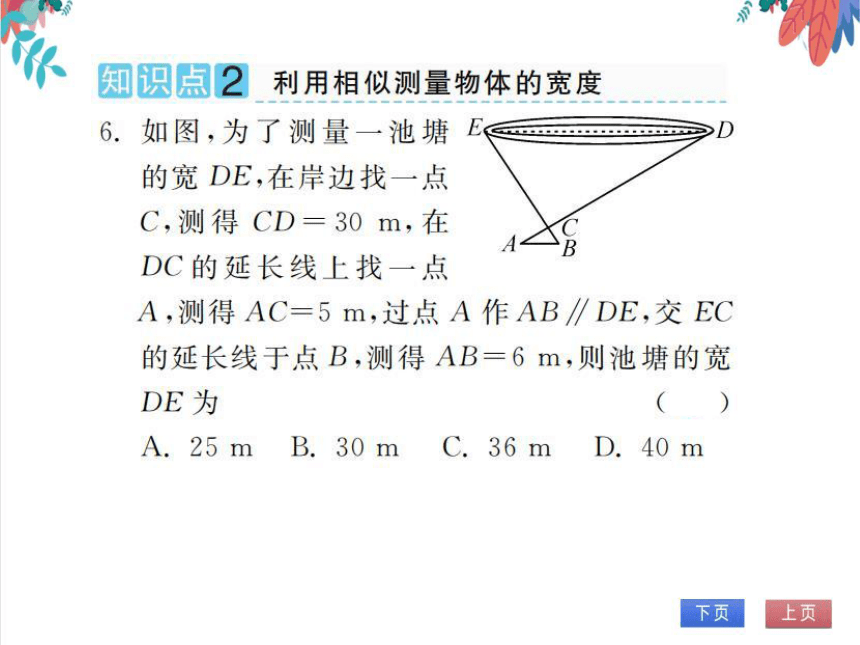
6.如图,为了测量一池塘F少D
的宽DE,在岸边找一点
C,测得CD=30m,在
DC的延长线上找一点
A,测得AC=5m,过点A作AB∥DE,交EC
的延长线于点B,测得AB=6m,则池塘的宽
DE为
(C)
A.25mB.30mC.36mD.40m
7.(陕西)周末,小华和小亮想用所学的数学知识
测量家门前小河的宽.测量时,他们选择了河
对岸边的一棵大树,将其底部作为点A,在他
们所在的岸边选择了点B,使得AB与河岸垂
直,并在B点竖起标杆BC,再在AB的延长线
上选择点D竖起标杆DE,使得点E与点C,A
共线.已知CB⊥AD,DE⊥AD,测得BC
1m,DE=1.5m,BD=8.5m,测量示意图如
图所示,请根据相关测量信息,求河宽AB
解:∵CB⊥AD,
ED⊥AD,
D
∠CBA=∠EDA=
90.∵∠CAB=∠EAD,
下页
上页
N课前预习
预习新知
利用三角形相似解决实际问题的一般步骤:(1)根据
题意画出示意图;(2)将题目中的已知量或已知
关系转化为示意图中的已知线段、已知角或它们
之间的关系;(3)利用相似三角形建立线段之间
的关系,求出未知量;(4)写出答案
知识点1利用相似测量物体的高度
1.如图,小明在地面上放了一个平面镜,选择合
适的位置,刚好在平面镜中看到旗杆的顶部
此时小明与平面镜的水平距离为2m,旗杆底
部与平面镜的水平距离为16m,若小明的眼睛与
地面的距离为1.5m,则旗杆的高度为(B
m B 12 m C.9 m D
16
(第1题图)
第2题图)
2.(天水)如图,某校数学兴趣小组利用标杆BE
测量建筑物的高度,已知标杆BE高1.5m,测
得AB=1.2m,BC=12.8m,则建筑物CD的
高是
(A)
A.17.5mB.17mC.16.5mD.18m
3.(绍兴)学校门口的栏杆如图所示,栏杆从水平
位置BD绕O点旋转到AC位置,已知AB⊥
BD,CD⊥BD,垂足分别为B,D,AO=4m,
AB=1.6m,CO=1m,则栏杆C端应下降的
垂直距离CD为0.4m
(第3题图
(第4题图
5.如图,有两堵墙AB,CD,AB墙高2m,两墙之
间的距离BC为8m,小明将一架木梯放在距
B点3m的E处靠向墙AB时,木梯有很多露
出墙外.将木梯绕点E旋转90°靠向墙CD时,
木梯刚好达到墙的顶点D,求墙CD的高
解:由题意可知∠B=∠C
D
90°,∠AED=90°,BE=3m,
:.CE-BC-BE==(m),B E
∠BAE+∠AEB=90°,∠AEB+∠DEC
90.∴∠BAE=∠DEC.∴△ABE∽△ECD
AB BE 2 3
EC DC
解得DC=7.5
因此墙CD的高为7.5m
知织点2利用相似测量物体的宽度
6.如图,为了测量一池塘F少D
的宽DE,在岸边找一点
C,测得CD=30m,在
DC的延长线上找一点
A,测得AC=5m,过点A作AB∥DE,交EC
的延长线于点B,测得AB=6m,则池塘的宽
DE为
(C)
A.25mB.30mC.36mD.40m
7.(陕西)周末,小华和小亮想用所学的数学知识
测量家门前小河的宽.测量时,他们选择了河
对岸边的一棵大树,将其底部作为点A,在他
们所在的岸边选择了点B,使得AB与河岸垂
直,并在B点竖起标杆BC,再在AB的延长线
上选择点D竖起标杆DE,使得点E与点C,A
共线.已知CB⊥AD,DE⊥AD,测得BC
1m,DE=1.5m,BD=8.5m,测量示意图如
图所示,请根据相关测量信息,求河宽AB
解:∵CB⊥AD,
ED⊥AD,
D
∠CBA=∠EDA=
90.∵∠CAB=∠EAD,
