【人教版】数学九年级下册 28.1 锐角三角函数 第1课时 正弦 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 28.1 锐角三角函数 第1课时 正弦 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 648.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览





文档简介
(共13张PPT)
下页
上页
课前预习
如图,在Rt△ABC中,∠C=90°,把锐角A的对
边与斜边的比叫做∠A的正弦,记作sinA,
即sinA=∠4的对边
斜边
当堂训练
巩固基
知识点1已知直角三角形的边长,求锐角的
正弦值
1.在Rt△ABC中,∠C=90°,若把各边的长都扩
大到原来的5倍,则∠A的正弦值
(C)
A.扩大到原来的5倍
B.缩小到原来的
C.不变
D.不能确定
2.在Rt△ABC中,∠C=90°,AB=5,AC=3,那
么sinA的值为
(B)
C
D
3.在△ABC中,∠C=90°,若AC=2BC,则sinA
的值为
(C)
B.2
5D.2
4.(聊城)如图,在4×5的正方形网格中,每个小
正方形的边长都是1,△ABC的顶点都在这些
小正方形的顶点上,那么sin∠ACB的值为
35
17
C
D
A
B
(第4题图)
(第5题图)
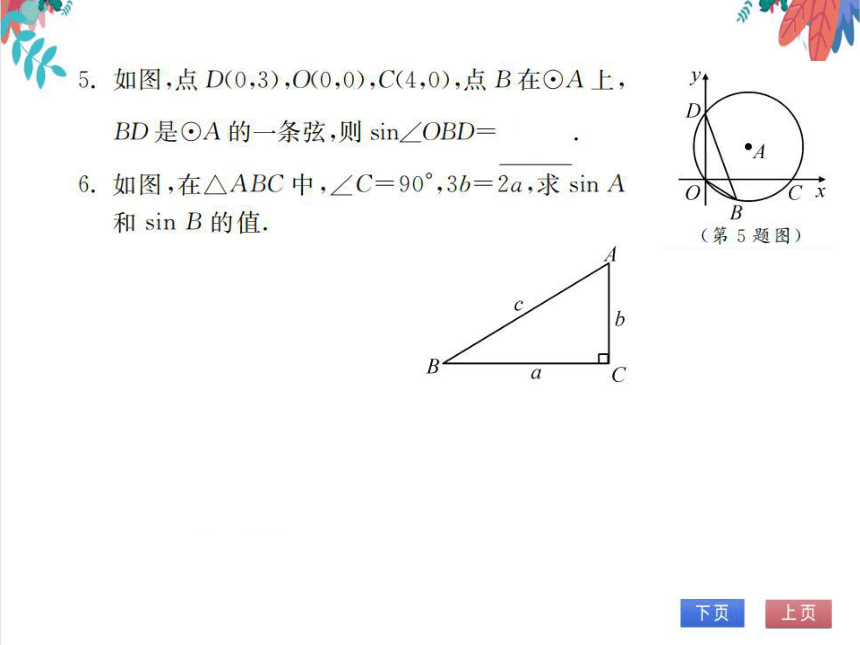
5.如图,点D(0,3),O(0,0),C(4,0),点B在⊙A上,
BD是⊙A的一条弦,则sin∠OBD=3
6.如图,在△ABC中,∠C=90°,3b=2a,求sinA
和sinB的值
解:∵3b=2a,∴a:b=3:2
设a=3x,b=2x
∵∠C=90°
tb
B
∴sinA=a
3
13
B
知织点2已知锐角的正弦值,求直角三角形
的边长
7.在△ABC中,∠C=90°,BC=6,sinA3
则
AB的值为
(C)
A.8
B.9
C.10
D.12
8.在Rt△ABC中,∠C=90°,sinB=0.5,若
AC=6,则BC=63
9.如图,在Rt△ABC中,∠C=90°,BC=4,sinA
求AC的长
解:在△ABC中,∠C=90°,B
∵sinA=BC_2
AB=2,BC=4,
∴AB=6.
在Rt△ABC中,
AC=√AB2BC=√62-42=25.
课后作业
全面提升
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB
于点D,若AC=√5,BC=2,则sin∠ACD的
值是
(A)
A
B
(第1题图)
(第2题图
2.如图,P是∠a的边OA上一点,点P的坐标
为(2,1),则sina的值为
(A)
A
B
3.如图,在矩形ABCD中,AB=3,AD=5,点E
在DC上,将矩形ABCD沿AE折叠,点D恰
好落在BC边上的点F处,那么sin∠EFC的
值为
C B
A
E
B
B
(第3题图)
第4题图)
4.(牡丹江)如图,△ABC内接于⊙O,若
sin∠BAC=1,BC=26,则⊙O的半径为
CA
A.3
B.6√6
下页
上页
课前预习
如图,在Rt△ABC中,∠C=90°,把锐角A的对
边与斜边的比叫做∠A的正弦,记作sinA,
即sinA=∠4的对边
斜边
当堂训练
巩固基
知识点1已知直角三角形的边长,求锐角的
正弦值
1.在Rt△ABC中,∠C=90°,若把各边的长都扩
大到原来的5倍,则∠A的正弦值
(C)
A.扩大到原来的5倍
B.缩小到原来的
C.不变
D.不能确定
2.在Rt△ABC中,∠C=90°,AB=5,AC=3,那
么sinA的值为
(B)
C
D
3.在△ABC中,∠C=90°,若AC=2BC,则sinA
的值为
(C)
B.2
5D.2
4.(聊城)如图,在4×5的正方形网格中,每个小
正方形的边长都是1,△ABC的顶点都在这些
小正方形的顶点上,那么sin∠ACB的值为
35
17
C
D
A
B
(第4题图)
(第5题图)
5.如图,点D(0,3),O(0,0),C(4,0),点B在⊙A上,
BD是⊙A的一条弦,则sin∠OBD=3
6.如图,在△ABC中,∠C=90°,3b=2a,求sinA
和sinB的值
解:∵3b=2a,∴a:b=3:2
设a=3x,b=2x
∵∠C=90°
tb
B
∴sinA=a
3
13
B
知织点2已知锐角的正弦值,求直角三角形
的边长
7.在△ABC中,∠C=90°,BC=6,sinA3
则
AB的值为
(C)
A.8
B.9
C.10
D.12
8.在Rt△ABC中,∠C=90°,sinB=0.5,若
AC=6,则BC=63
9.如图,在Rt△ABC中,∠C=90°,BC=4,sinA
求AC的长
解:在△ABC中,∠C=90°,B
∵sinA=BC_2
AB=2,BC=4,
∴AB=6.
在Rt△ABC中,
AC=√AB2BC=√62-42=25.
课后作业
全面提升
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB
于点D,若AC=√5,BC=2,则sin∠ACD的
值是
(A)
A
B
(第1题图)
(第2题图
2.如图,P是∠a的边OA上一点,点P的坐标
为(2,1),则sina的值为
(A)
A
B
3.如图,在矩形ABCD中,AB=3,AD=5,点E
在DC上,将矩形ABCD沿AE折叠,点D恰
好落在BC边上的点F处,那么sin∠EFC的
值为
C B
A
E
B
B
(第3题图)
第4题图)
4.(牡丹江)如图,△ABC内接于⊙O,若
sin∠BAC=1,BC=26,则⊙O的半径为
CA
A.3
B.6√6
