【人教版】数学九年级下册 28.2.2 应用举例 第3课时 坡度(或坡比)与解直角三角形 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 28.2.2 应用举例 第3课时 坡度(或坡比)与解直角三角形 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 820.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览




文档简介
(共16张PPT)
下页
上页
课前预习
预习新知
1.如图,坡度(或坡比)是坡面铅直高度与
水平距离的比,通常用i表示,一般写成
h,坡角a与坡度的关系是tana=/=n
坡面距离
铅直高度
l水平距离
(第1题图)
(第2题图)
2.如图,解与梯形有关的工程问题时,通常作
高,把它转化成直角三角形和矩形,
进而解决问题
当堂训练巩面基础
知织点1坡度(或坡比)的认识
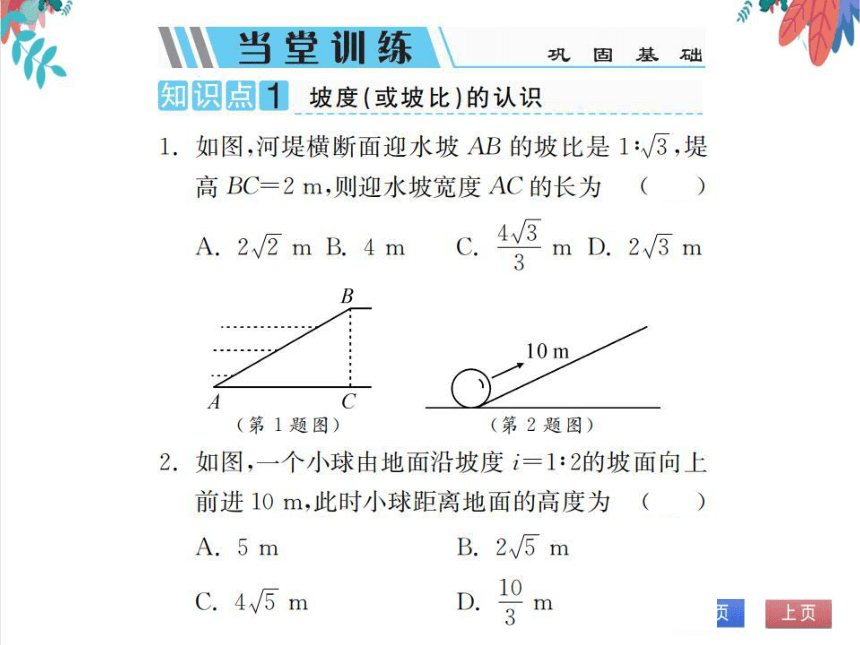
1.如图,河堤横断面迎水坡AB的坡比是1:3,堤
高BC=2m,则迎水坡宽度AC的长为(D)
A.2√2mB.4mC
3mD.2√3m
10
(第1题图)
(第2题图)
2.如图,一个小球由地面沿坡度i=1:2的坡面向上
前进10m,此时小球距离地面的高度为(B)
B.2
C.4
10
m
知织点2坡度(或坡比)与实际问题
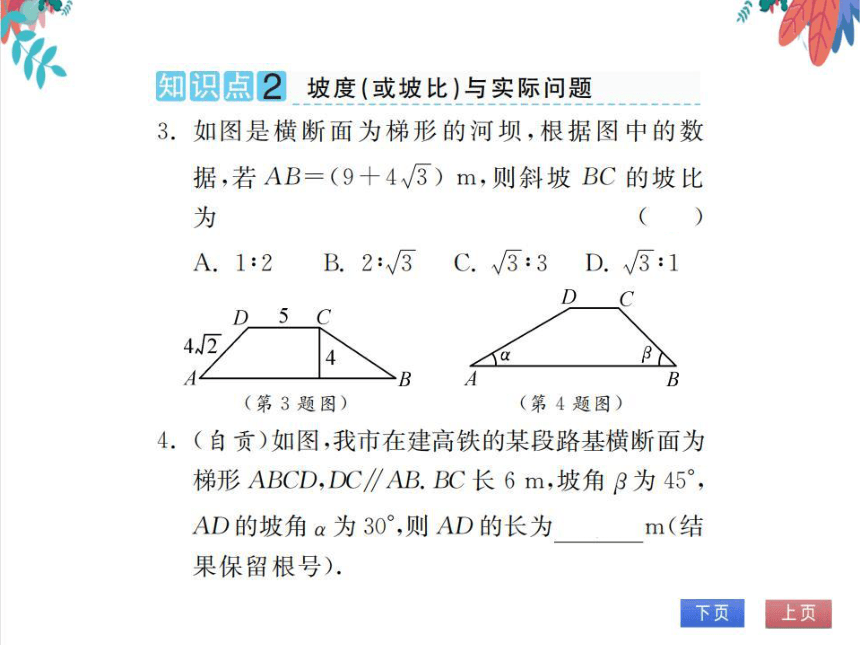
如图是横断面为梯形的河坝,根据图中的数
据,若AB=(9+43)m,则斜坡BC的坡比
为
(C)
A.1:2B.2:3C.√3:3D.√3:1
42
4
B
B
(第3题图)
(第4题图)
4.(自贡)如图,我市在建高铁的某段路基横断面为
梯形ABCD,DC∥AB.BC长6m,坡角B为45°,
AD的坡角a为30°,则AD的长为62m(结
果保留根号)
5.(湘潭)为了学生的安全,某校决定把一段如图
所示的步梯路段进行改造.已知四边形ABCD
为矩形,DE=10m,其坡度为i1=1:3,将步
梯DE改造为斜坡AF,其坡度为i2=1:4,求
斜坡AF的长度(结果精确到0.1m,参考数
据:3≈1.732,√17≈4.123)
解:∵DE=10m,其坡度
为i1=1:3,
∴在Rt△DCE中,
DE=DC2+CE2=2DC=10
∴解得DC=5.∵四边形ABCD为矩形,
∴AB=CD=5.∵斜坡AF的坡度为i2=1:4
6.如图,某仓储中心有一斜坡AB,其坡度为i
1:2,矩形DEFG为长方体货柜的侧面图,其
中DE=2.5m,EF=2m.将该货柜沿斜坡向
上运送,当BF=3.5m时,求点D离地面的高
(5≈2.236,结果精确到0.1m)
解:如图,过点D作
DN⊥BC分别交AB,
E
BC于点M,N
证∠GDM=∠MBN,
GM 1
tan/GDM
∴GM=1m,求得DM=√5m
∴FM=2.5-1=1.5(m).∴BM=5m.
在Rt△BNM中,tan∠MBN
MN 1
bN2
设MN=xm,BN=2xm,
∴BM=√5xm.∴x=√5
∴MN=5m.∴DN=2√5≈4.5m
答:点D离地面的高为4.5m
下页
上页
课前预习
预习新知
1.如图,坡度(或坡比)是坡面铅直高度与
水平距离的比,通常用i表示,一般写成
h,坡角a与坡度的关系是tana=/=n
坡面距离
铅直高度
l水平距离
(第1题图)
(第2题图)
2.如图,解与梯形有关的工程问题时,通常作
高,把它转化成直角三角形和矩形,
进而解决问题
当堂训练巩面基础
知织点1坡度(或坡比)的认识
1.如图,河堤横断面迎水坡AB的坡比是1:3,堤
高BC=2m,则迎水坡宽度AC的长为(D)
A.2√2mB.4mC
3mD.2√3m
10
(第1题图)
(第2题图)
2.如图,一个小球由地面沿坡度i=1:2的坡面向上
前进10m,此时小球距离地面的高度为(B)
B.2
C.4
10
m
知织点2坡度(或坡比)与实际问题
如图是横断面为梯形的河坝,根据图中的数
据,若AB=(9+43)m,则斜坡BC的坡比
为
(C)
A.1:2B.2:3C.√3:3D.√3:1
42
4
B
B
(第3题图)
(第4题图)
4.(自贡)如图,我市在建高铁的某段路基横断面为
梯形ABCD,DC∥AB.BC长6m,坡角B为45°,
AD的坡角a为30°,则AD的长为62m(结
果保留根号)
5.(湘潭)为了学生的安全,某校决定把一段如图
所示的步梯路段进行改造.已知四边形ABCD
为矩形,DE=10m,其坡度为i1=1:3,将步
梯DE改造为斜坡AF,其坡度为i2=1:4,求
斜坡AF的长度(结果精确到0.1m,参考数
据:3≈1.732,√17≈4.123)
解:∵DE=10m,其坡度
为i1=1:3,
∴在Rt△DCE中,
DE=DC2+CE2=2DC=10
∴解得DC=5.∵四边形ABCD为矩形,
∴AB=CD=5.∵斜坡AF的坡度为i2=1:4
6.如图,某仓储中心有一斜坡AB,其坡度为i
1:2,矩形DEFG为长方体货柜的侧面图,其
中DE=2.5m,EF=2m.将该货柜沿斜坡向
上运送,当BF=3.5m时,求点D离地面的高
(5≈2.236,结果精确到0.1m)
解:如图,过点D作
DN⊥BC分别交AB,
E
BC于点M,N
证∠GDM=∠MBN,
GM 1
tan/GDM
∴GM=1m,求得DM=√5m
∴FM=2.5-1=1.5(m).∴BM=5m.
在Rt△BNM中,tan∠MBN
MN 1
bN2
设MN=xm,BN=2xm,
∴BM=√5xm.∴x=√5
∴MN=5m.∴DN=2√5≈4.5m
答:点D离地面的高为4.5m
