【人教版】数学九年级下册 第27章 专题九 专题十 相似三角形与面积、动点问题中的相似 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第27章 专题九 专题十 相似三角形与面积、动点问题中的相似 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 756.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览




文档简介
(共18张PPT)
下页
上页
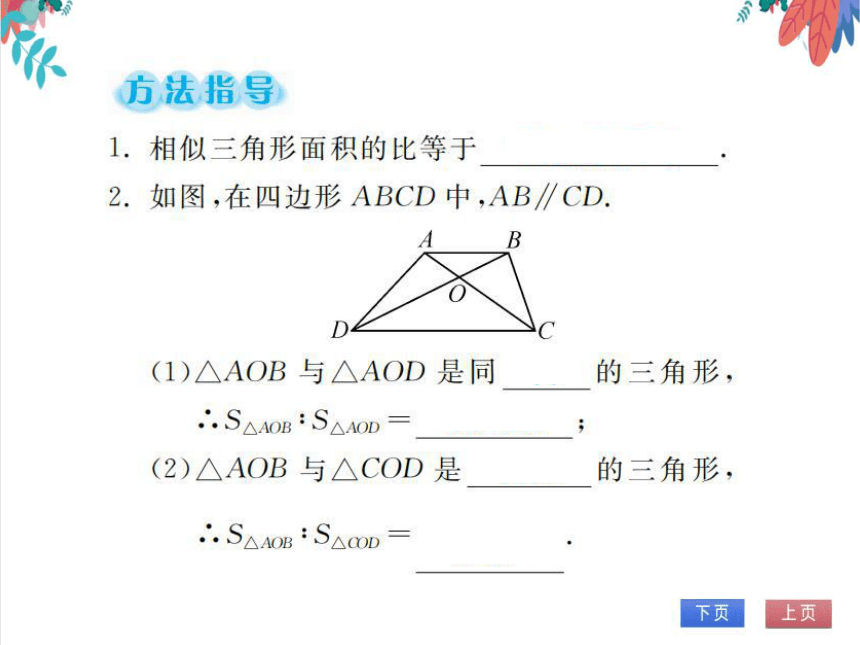
方法指导
相似三角形面积的比等于相似比的平方
2.如图,在四边形ABCD中,AB∥CD
D
(1)△AOB与△AOD是同高的三角形,
∴S△AOB:S
△AOD
OB: OD
(2)△AOB与△COD是相似的三角形,
AB
·△AOB"△OOD
CD
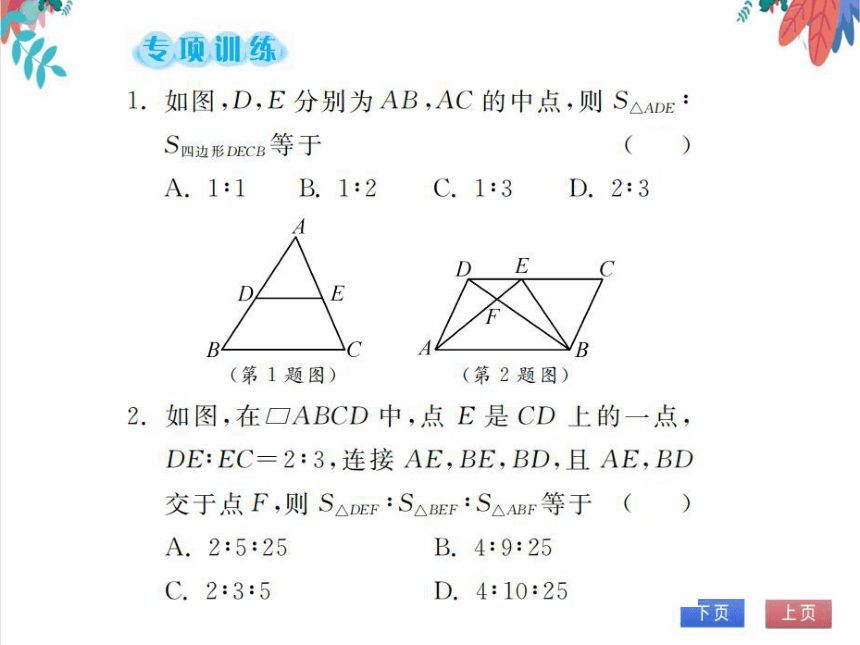
专顶训练
1.如图,D,E分别为AB,AC的中点,则S
△ADE
四边形DECB
等于
(C)
A.1:1B.1:2C.1:3D.2:3
(第1题图)
(第2题图)
2.如图,在□ABCD中,点E是CD上的一点,
DE:EC=2:3,连接AE,BE,BD,且AE,BD
交于点F,则S△DEF:S△BF:S△ABF等于(D)
A.2:5:25
B.4:9:25
C.2:3:5
D.4:10:25
3.(包头)如图,在□ABCD中,AC是对角线,点E
在边AB上,EF∥BC交AC于点F,若3AE
2EB,S△AEF=1,则S△ADF=5
D
F
BE C
(第3题图)
(第4题图)
4.(泸州)如图,在边长为4的正方形ABCD中,
点E是BC的中点,点F在CD上,且CF
3DF,AE,BF相交于点G,则△AGF的面积
56
是
5.如图,D,E分别是AB,AC的中点,DF过EC
的中点G,且交BE于点O,若S△ADE=a
(1)求证:OD=OG;
(2)求四边形BOGC的面积
(1)证明:∵D,E分别是AB,
AC的中点,
∴DE∥BF,BC=2DE
E
△DEGC△FCG
DG EG DE
F
GF GC CF
∵EG=CG,∴.DG=GF,DE=CF
同理△DOE∽△FOB,∴
DE OE OD
BF OB OF
OE OD
DG 1
OBOF3··GF1
∴OD=+DF,即OD=OG.
(2)解:∵DO=GO,…∴S△aE=S△oE.∵OE:OB=1:3,
DE
设S△Bx1=S,∴S△BE=S.∴S△BD=3S
△BOD
△BDE
4S.∴S
△ABE
8S
△BEC
8S
四边形BOGC
△BEC
△OOE
8S-S=75
∵:S△AME=a=4S,∴S=.∴.S四边形B=4a
6.如图,在△ABC中,点P是BC边上任意一点
(点P与点B,C不重合),□AFPE的顶点F
E分别在AB,AC上.已知BC=2,S△ABC=1
设BP=x,□AFPE的面积为y
(1)求y与x的函数关系式;
(2)上述函数有最大值或最小值吗 若有,则
当x取何值时,y有这样的值,并求出该
值;若没有,请说明理由
下页
上页
方法指导
相似三角形面积的比等于相似比的平方
2.如图,在四边形ABCD中,AB∥CD
D
(1)△AOB与△AOD是同高的三角形,
∴S△AOB:S
△AOD
OB: OD
(2)△AOB与△COD是相似的三角形,
AB
·△AOB"△OOD
CD
专顶训练
1.如图,D,E分别为AB,AC的中点,则S
△ADE
四边形DECB
等于
(C)
A.1:1B.1:2C.1:3D.2:3
(第1题图)
(第2题图)
2.如图,在□ABCD中,点E是CD上的一点,
DE:EC=2:3,连接AE,BE,BD,且AE,BD
交于点F,则S△DEF:S△BF:S△ABF等于(D)
A.2:5:25
B.4:9:25
C.2:3:5
D.4:10:25
3.(包头)如图,在□ABCD中,AC是对角线,点E
在边AB上,EF∥BC交AC于点F,若3AE
2EB,S△AEF=1,则S△ADF=5
D
F
BE C
(第3题图)
(第4题图)
4.(泸州)如图,在边长为4的正方形ABCD中,
点E是BC的中点,点F在CD上,且CF
3DF,AE,BF相交于点G,则△AGF的面积
56
是
5.如图,D,E分别是AB,AC的中点,DF过EC
的中点G,且交BE于点O,若S△ADE=a
(1)求证:OD=OG;
(2)求四边形BOGC的面积
(1)证明:∵D,E分别是AB,
AC的中点,
∴DE∥BF,BC=2DE
E
△DEGC△FCG
DG EG DE
F
GF GC CF
∵EG=CG,∴.DG=GF,DE=CF
同理△DOE∽△FOB,∴
DE OE OD
BF OB OF
OE OD
DG 1
OBOF3··GF1
∴OD=+DF,即OD=OG.
(2)解:∵DO=GO,…∴S△aE=S△oE.∵OE:OB=1:3,
DE
设S△Bx1=S,∴S△BE=S.∴S△BD=3S
△BOD
△BDE
4S.∴S
△ABE
8S
△BEC
8S
四边形BOGC
△BEC
△OOE
8S-S=75
∵:S△AME=a=4S,∴S=.∴.S四边形B=4a
6.如图,在△ABC中,点P是BC边上任意一点
(点P与点B,C不重合),□AFPE的顶点F
E分别在AB,AC上.已知BC=2,S△ABC=1
设BP=x,□AFPE的面积为y
(1)求y与x的函数关系式;
(2)上述函数有最大值或最小值吗 若有,则
当x取何值时,y有这样的值,并求出该
值;若没有,请说明理由
