【人教版】数学九年级下册 第27章 专题六 相似三角形中的基本模型 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第27章 专题六 相似三角形中的基本模型 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 631.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览





文档简介
(共15张PPT)
下页
上页
类型1“A”字型
E
B
c B
C B
C
1.如图,AD,BE是△ABC的两条高
(1)求证:CE·CA=CD·CB;
(2)若EC=5,BC=13,求的值.
(1)证明:∵AD,BE是△ABC
的两条高,
E
∴∠ADC=∠BEC=90
又∵∠C=∠C,
∴△ACDC△BCE
CD=CA,即CE·CA=CD·CB
(2)解
CE CB CE CD
CD CA CB CA
又∵∠C=∠C,EC=5,BC=13,
∴△CDE∽△CAB.、DECE5
AB BC 13
2.(贵港改编)如图,在△ABC中,点D,E分别在
AB,AC边上,DE∥BC,AD=2BD,BC=6
(1)求DE的长
(2)连接CD,若∠ACD=∠B,求CD的长
解:(1)∵AD=2BD,∴AB=
AD+BD=3BD.∵DE∥BC,
∴△ADE∽△ABC.…∴E
BC
B
AE AD 2 DE
∴DE=4
AC AB 3
(2)∵DE∥BC,∴∠CDE=∠BCD
又∵∠ACD=∠B,∴△BCD∽△CDE
CD BC
DEC∴CD2=DE·BC=4×6=24
∴CD=2√6
类型2“X”字型
B
△D
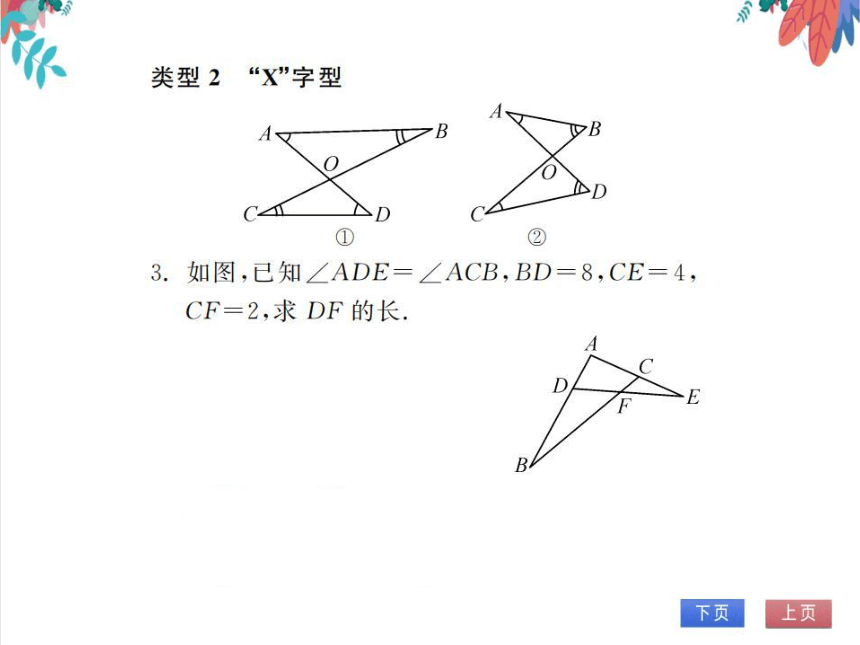
3.如图,已知∠ADE=∠ACB,BD=8,CE=4,
CF=2,求DF的长
解:∵∠ADE+∠BDE
180°,∠ACB+∠ECB
E
180°,∠ADE=∠ACB,
∴∠BDE=∠ECB
又∵∠DFB=∠EFC,∴△BDF∽△ECF
.BD=DF,即8=DF
EC CF
,解得DF=4
4.(张家界)如图,在平行四边形ABCD中,连接
对角线AC,延长AB至点E,使BE=AB,连
接DE分别交BC,AC于点F,G
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长
(1)证明:∵四边形ABCD
D
是平行四边形,∴AD∥CB,
AD=BC
∴△EBF∽△EAD
BFEB=1.∴BF=2AD=2
AD EA
BC
∴BF=CF
类型3“双垂直”型
如图,直角三角形被斜边上的高分成的两个直角三
角形与原三角形相似,即△ACD△ABC△CBD
相关结论
CD2=AD·BD;
AC2=AD·AB;
BC2=BD·AB
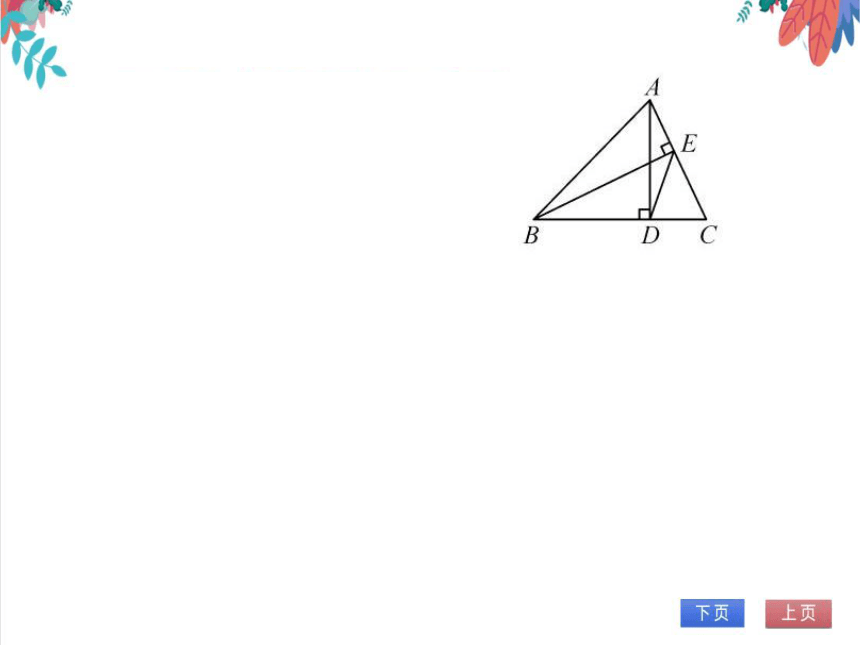
5.如图,在Rt△ABC中,∠BAC=90,AD⊥BC
于点D,DE⊥AC于点E,DF⊥AB于点F,请
说明△AEF∽△ABC的理由
下页
上页
类型1“A”字型
E
B
c B
C B
C
1.如图,AD,BE是△ABC的两条高
(1)求证:CE·CA=CD·CB;
(2)若EC=5,BC=13,求的值.
(1)证明:∵AD,BE是△ABC
的两条高,
E
∴∠ADC=∠BEC=90
又∵∠C=∠C,
∴△ACDC△BCE
CD=CA,即CE·CA=CD·CB
(2)解
CE CB CE CD
CD CA CB CA
又∵∠C=∠C,EC=5,BC=13,
∴△CDE∽△CAB.、DECE5
AB BC 13
2.(贵港改编)如图,在△ABC中,点D,E分别在
AB,AC边上,DE∥BC,AD=2BD,BC=6
(1)求DE的长
(2)连接CD,若∠ACD=∠B,求CD的长
解:(1)∵AD=2BD,∴AB=
AD+BD=3BD.∵DE∥BC,
∴△ADE∽△ABC.…∴E
BC
B
AE AD 2 DE
∴DE=4
AC AB 3
(2)∵DE∥BC,∴∠CDE=∠BCD
又∵∠ACD=∠B,∴△BCD∽△CDE
CD BC
DEC∴CD2=DE·BC=4×6=24
∴CD=2√6
类型2“X”字型
B
△D
3.如图,已知∠ADE=∠ACB,BD=8,CE=4,
CF=2,求DF的长
解:∵∠ADE+∠BDE
180°,∠ACB+∠ECB
E
180°,∠ADE=∠ACB,
∴∠BDE=∠ECB
又∵∠DFB=∠EFC,∴△BDF∽△ECF
.BD=DF,即8=DF
EC CF
,解得DF=4
4.(张家界)如图,在平行四边形ABCD中,连接
对角线AC,延长AB至点E,使BE=AB,连
接DE分别交BC,AC于点F,G
(1)求证:BF=CF;
(2)若BC=6,DG=4,求FG的长
(1)证明:∵四边形ABCD
D
是平行四边形,∴AD∥CB,
AD=BC
∴△EBF∽△EAD
BFEB=1.∴BF=2AD=2
AD EA
BC
∴BF=CF
类型3“双垂直”型
如图,直角三角形被斜边上的高分成的两个直角三
角形与原三角形相似,即△ACD△ABC△CBD
相关结论
CD2=AD·BD;
AC2=AD·AB;
BC2=BD·AB
5.如图,在Rt△ABC中,∠BAC=90,AD⊥BC
于点D,DE⊥AC于点E,DF⊥AB于点F,请
说明△AEF∽△ABC的理由
