【人教版】数学九年级下册 第27章 专题七 、专题八 等级式或比例式的证明、圆与相似三角形 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第27章 专题七 、专题八 等级式或比例式的证明、圆与相似三角形 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 698.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览






文档简介
(共17张PPT)
下页
上页
专顶训练
类型1三点定形法
1.(上海改编)如图,在菱形ABCD中,点E,F分
别在边AB,AD上,BE=DF,CE的延长线交
DA的延长线于点G,CF的延长线交BA的延
长线于点H.求证:BC2=BE·BH.
证明:∵四边形ABCD是
菱形,∴CD=CB,∠D=D
B
∠B.∵∴DF=BE,
∴△CDF≌CBE(SAS)
∴∠DCF=∠BCE.∵CD∥BH
∴∠H=∠DCF.∴∠BCE=∠H
∵∠B=∠B,∴△BEC∽△BCH
BE BC
BCB.∴BC2=BE·BH
类型2等线段代换法
2.(泰安改编)如图,在矩形ABCD中,AE⊥BD
于点E,点P是边AD上一点.若PE⊥EC,求
证:AE·AB=DE·AP
证明:∵四边形ABCD是矩
形,∴∠BAD=∠ADC
90°,AB=CD
B
AE⊥BD,PE⊥EC,
∴∠AED=∠PEC=90°.
∠AEP=∠DEC
∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,
∴∠EAP=∠EDC.∴△AEPC△DEC
AE AP
DEn∴∵AB=CD,
∴AE·AB=DE·AP
3.如图,已知AD平分∠BAC,AD的垂直平分
线EP交BC的延长线于点P.求证:PD2
PB·PC
证明:如图,连接PA.由
AD的中垂线得PA=PD,
∴∠PDA=∠PAD
∵∠PDA=∠B+∠BAD,
∠PAD=∠PAC+∠DAC,
AD平分∠BAC,∴∠BAD=∠CAD
∴∠B=∠PAC.∵∠APC=∠BPA
△PAC∽△PBA∴APC
PB PA
∴PA2=PB·PC.
∴PA=PD,PD2=PB·PC
类型3等比代换法
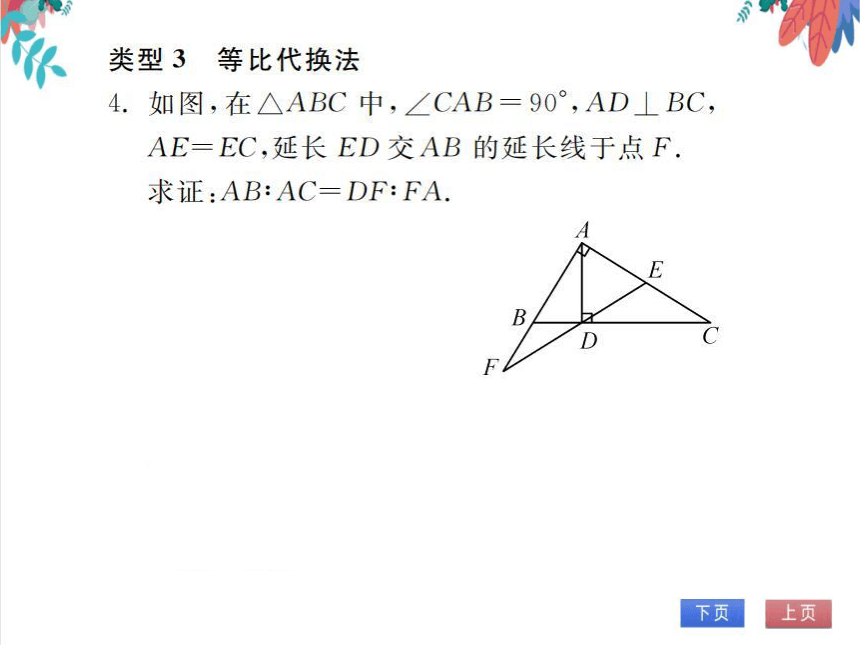
4.如图,在△ABC中,∠CAB=90°,AD⊥BC,
AE=EC,延长ED交AB的延长线于点F
求证:AB:AC=DF:FA
证明:证△BAD△ACD,
AB BD
得
AC AD
D
证∠BAD=∠C=
∠CDE=∠FDB,
DE BD
得△FBD∽△FDA,∴
AF AD
AB
AC=FA,即AB:AC=DF:FA
类型4等积过渡法
5.如图,AD是△ABC的高,DE⊥AB于点E,
DF⊥AC于点F.求证:AE·AB=AF·AC.
证明:∵AD是△ABC的高,
DE⊥AB,
∴∠AED=∠ADB=∠ADC
F
90.∵∠BAD=∠EAD,
∴△AED△ADB.EAAD
AD AB
∴AD2=AE·AB.同理可证明AD2=AF
AC,∴AE·AB=AF·AC
下页
上页
专顶训练
类型1三点定形法
1.(上海改编)如图,在菱形ABCD中,点E,F分
别在边AB,AD上,BE=DF,CE的延长线交
DA的延长线于点G,CF的延长线交BA的延
长线于点H.求证:BC2=BE·BH.
证明:∵四边形ABCD是
菱形,∴CD=CB,∠D=D
B
∠B.∵∴DF=BE,
∴△CDF≌CBE(SAS)
∴∠DCF=∠BCE.∵CD∥BH
∴∠H=∠DCF.∴∠BCE=∠H
∵∠B=∠B,∴△BEC∽△BCH
BE BC
BCB.∴BC2=BE·BH
类型2等线段代换法
2.(泰安改编)如图,在矩形ABCD中,AE⊥BD
于点E,点P是边AD上一点.若PE⊥EC,求
证:AE·AB=DE·AP
证明:∵四边形ABCD是矩
形,∴∠BAD=∠ADC
90°,AB=CD
B
AE⊥BD,PE⊥EC,
∴∠AED=∠PEC=90°.
∠AEP=∠DEC
∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,
∴∠EAP=∠EDC.∴△AEPC△DEC
AE AP
DEn∴∵AB=CD,
∴AE·AB=DE·AP
3.如图,已知AD平分∠BAC,AD的垂直平分
线EP交BC的延长线于点P.求证:PD2
PB·PC
证明:如图,连接PA.由
AD的中垂线得PA=PD,
∴∠PDA=∠PAD
∵∠PDA=∠B+∠BAD,
∠PAD=∠PAC+∠DAC,
AD平分∠BAC,∴∠BAD=∠CAD
∴∠B=∠PAC.∵∠APC=∠BPA
△PAC∽△PBA∴APC
PB PA
∴PA2=PB·PC.
∴PA=PD,PD2=PB·PC
类型3等比代换法
4.如图,在△ABC中,∠CAB=90°,AD⊥BC,
AE=EC,延长ED交AB的延长线于点F
求证:AB:AC=DF:FA
证明:证△BAD△ACD,
AB BD
得
AC AD
D
证∠BAD=∠C=
∠CDE=∠FDB,
DE BD
得△FBD∽△FDA,∴
AF AD
AB
AC=FA,即AB:AC=DF:FA
类型4等积过渡法
5.如图,AD是△ABC的高,DE⊥AB于点E,
DF⊥AC于点F.求证:AE·AB=AF·AC.
证明:∵AD是△ABC的高,
DE⊥AB,
∴∠AED=∠ADB=∠ADC
F
90.∵∠BAD=∠EAD,
∴△AED△ADB.EAAD
AD AB
∴AD2=AE·AB.同理可证明AD2=AF
AC,∴AE·AB=AF·AC
