【人教版】数学九年级下册 第27章 专题十一 相似与函数 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第27章 专题十一 相似与函数 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 766.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
下页
上页
方法指导
相似与函数是近年来中考命题的一个热点.一般
需要作垂线,构造直角三角形,得到线段之间的
关系,进一步转化为坐标关系,再列方程求解.解
题的关键是要正确处理点的坐标与线段的长度
之间的关系
专顶训练
类型1相似与一次函数
1.直线y=x+3交x轴、y轴于点A,B.动点
P从点A出发以每秒2个单位长度的速度向
点B运动,动点Q从点B出发以每秒1个单
位长度的速度向点O运动,其中一个动点到
达终点时,另一个动点也随之停止运动.当t
113时,△BPQ与△BAO相似
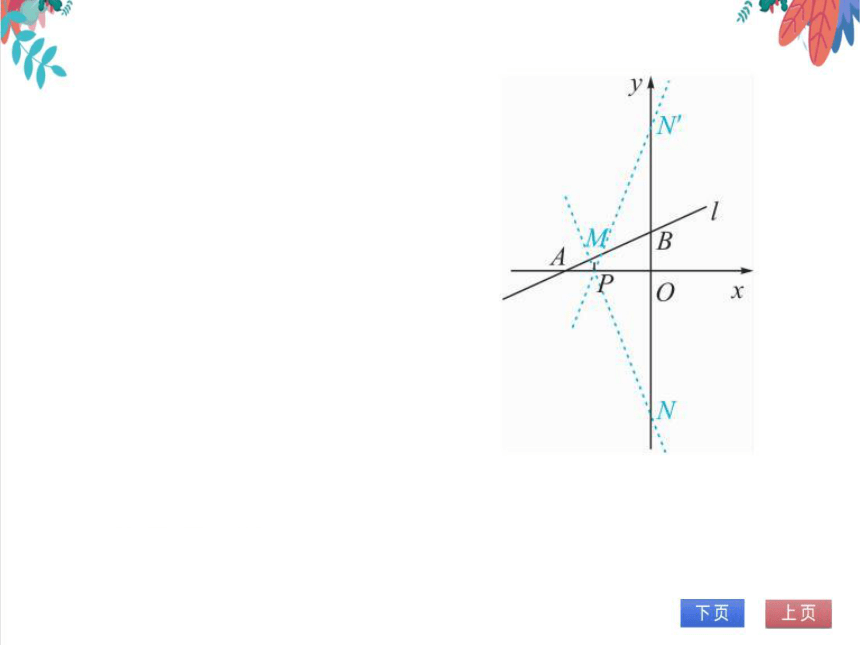
2.设一次函数y=2x+2的图象为直线l,直线l
与x轴、y轴分别交于点A,B,如图
(1)求点A和点B的坐标;
(2)直线m过点P(-3,0),若直线l,m与x轴
围成的三角形和直线l,m与y轴围成的
角形相似,求直线m与y轴的交点N的
坐标
解:(1)当x=0时,y=2
当y=0时,x=-4
故A(-4,0),B(0,2)
(2)①设直线m与直线l的交点
B
为M,与y轴的交点为N.
P
∵△APMo△NBM,
ON
∴△PON∽△BOA.∴
OA
OP ON 3
OB
∴ON=6
∴N(0,-6)
类型2相似与反比例函数
3.(鄂尔多斯)如图,点A(-2,0),B(0,1),以线
段AB为边在第二象限作矩形ABCD,双曲线
y=(k<0)过点D,连接BD,若四边形
OADB的面积为6,则k的值是
(C)
B.-12C.-16D.-18
y
P
(第3题图)
(第4题图)
4.(遵义)如图,△ABO的顶点A在函数y
k
(x>0)的图象上,∠ABO=90°,过AO边的三
等分点M,N分别作x轴的平行线交AB于点
P,Q.若四边形MNQP的面积为3,则k的值
为
(D)
A.9
B.12
D.18
5.如图,等边△OAB的边AB与y轴交于点C,
点A是反比例函数y=5(x>0)的图象上
点,且BC=2AC,则等边△OAB的边长为
2√7
B
(第5题图)
(第6题图)
7.(枣庄)如图,一次函数y=kx+b(k,b为常数
k≠0)的图象与x轴、y轴分别交于A,B两
点,且与反比例函数y=(n为常数,n≠0)的
图象在第二象限交于点C.CD⊥x轴,垂足为
D,若OB=2OA=3OD=12
(1)求一次函数与反比例函数的解析式;
下页
上页
方法指导
相似与函数是近年来中考命题的一个热点.一般
需要作垂线,构造直角三角形,得到线段之间的
关系,进一步转化为坐标关系,再列方程求解.解
题的关键是要正确处理点的坐标与线段的长度
之间的关系
专顶训练
类型1相似与一次函数
1.直线y=x+3交x轴、y轴于点A,B.动点
P从点A出发以每秒2个单位长度的速度向
点B运动,动点Q从点B出发以每秒1个单
位长度的速度向点O运动,其中一个动点到
达终点时,另一个动点也随之停止运动.当t
113时,△BPQ与△BAO相似
2.设一次函数y=2x+2的图象为直线l,直线l
与x轴、y轴分别交于点A,B,如图
(1)求点A和点B的坐标;
(2)直线m过点P(-3,0),若直线l,m与x轴
围成的三角形和直线l,m与y轴围成的
角形相似,求直线m与y轴的交点N的
坐标
解:(1)当x=0时,y=2
当y=0时,x=-4
故A(-4,0),B(0,2)
(2)①设直线m与直线l的交点
B
为M,与y轴的交点为N.
P
∵△APMo△NBM,
ON
∴△PON∽△BOA.∴
OA
OP ON 3
OB
∴ON=6
∴N(0,-6)
类型2相似与反比例函数
3.(鄂尔多斯)如图,点A(-2,0),B(0,1),以线
段AB为边在第二象限作矩形ABCD,双曲线
y=(k<0)过点D,连接BD,若四边形
OADB的面积为6,则k的值是
(C)
B.-12C.-16D.-18
y
P
(第3题图)
(第4题图)
4.(遵义)如图,△ABO的顶点A在函数y
k
(x>0)的图象上,∠ABO=90°,过AO边的三
等分点M,N分别作x轴的平行线交AB于点
P,Q.若四边形MNQP的面积为3,则k的值
为
(D)
A.9
B.12
D.18
5.如图,等边△OAB的边AB与y轴交于点C,
点A是反比例函数y=5(x>0)的图象上
点,且BC=2AC,则等边△OAB的边长为
2√7
B
(第5题图)
(第6题图)
7.(枣庄)如图,一次函数y=kx+b(k,b为常数
k≠0)的图象与x轴、y轴分别交于A,B两
点,且与反比例函数y=(n为常数,n≠0)的
图象在第二象限交于点C.CD⊥x轴,垂足为
D,若OB=2OA=3OD=12
(1)求一次函数与反比例函数的解析式;
