【人教版】数学九年级下册 第28章 整合与提高 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第28章 整合与提高 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 789.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
下页
上页
考点专训
考点1锐角三角函数的意义
例1如图,在△ABC中,∠C=90°,AD是中线,
BD=4,AD=25,则tan∠CAD的值为(A)
A.2
B.√2
C.√3
D
例2(广州)在Rt△ABC中,∠C=90°,tanA
15
,BC=15,则AB=17
【点拨】解决此类问题要注意:(1)必须在直角三
角形中;(2)明确直角三角形边之间关系所表示
的锐角三角函数;(3)运用锐角三角函数求边长
或求三角函数值时常需结合勾股定理来解答.
考点2特殊角的三角函数值
例3(安徽)如图,O的半径为1,△ABC内接
于⊙O.若∠A=60°,∠B=75°,则AB=√2.
例4(广元改编)计算:2sin45°
1-2+(2020-x)+2sin60
解:原式=2Xy
2-4-(2-1)+1+2×3
解:在Rt△ABC中,∠C=90°,B1
an A
3……·∠A=30°,
∠ABC=60.∵BD是∠ABC的平分线
∴∠CBD=∠ABD=30°.又∵CD=√3
∴BC=CD
tan 30
在Rt△ABC中,∠C=90°,∠A=30°,
BO
∴AB
sin30°6
考点4解直角三角形的实际应用
例6(泰安)如图,为了测量
某建筑物BC的高度,小颖采
E D
用了如下的方法:先从与建筑
物底端B在同一水平线上的B
A点出发,沿斜坡AD行走130m至坡顶D处,
再从D处沿水平方向继续前行若干米后至点E
处,在E点测得该建筑物顶端C的仰角为60°,建
筑物底端B的俯角为45°,点A,B,C,D,E在同
平面内,斜坡AD的坡度i=1:2.4.根据小颖的
测量数据,计算出建筑物BC的高度约为(参考数
据:3≈1.732)
(A)
A.136.6m
B.86.7m
C.186.7m
D.86.6m
【点拨】利用解直角三角形知识解决实际问题的
关键是将实际问题转化为数学问题,选择或构造
合适的直角三角形进行求解
2.如图,在菱形ABCD中,DE⊥AB,cosA3
BE=2,则tan∠DBE的值为
(B)
A.1
(第2题图)
(第3题图)
3.如图,⊙O的直径AB垂直于弦CD于点E,
∠A=22.5°,OC=4,则CD的长为(C)
A.22B.4
C.4
D.8
4.如图,小明要测量河内小岛B到河边公路L的
距离,在A点测得∠BAD=30°,在C点测得
∠BCD=60°,又测得AC=50m,则小岛B到
公路l的距离为
(B)
A.25m
B
100√3
m
D.(25+253)m
B
C
D
B
(第4题图)
(第6题图)
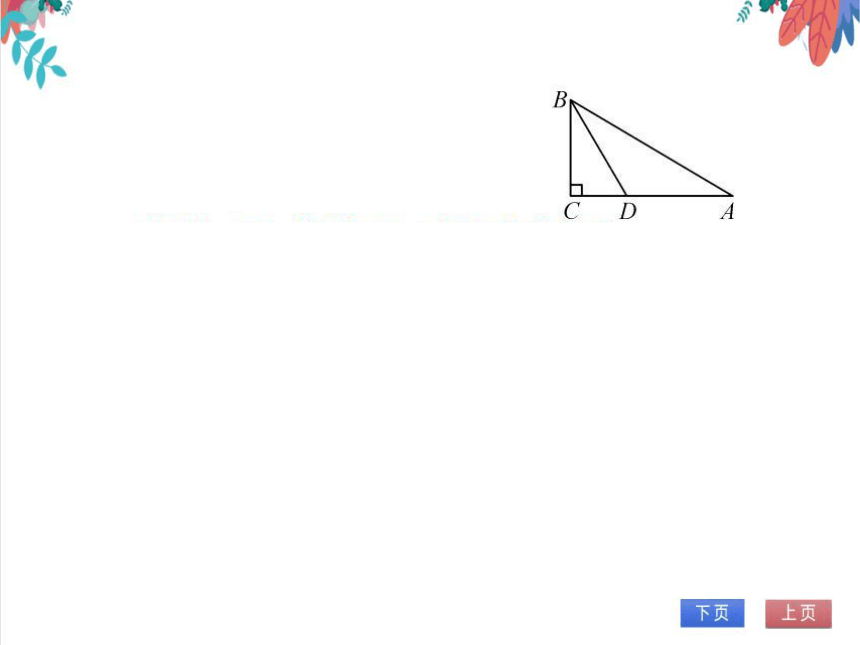
5.(易错题)已知AD是△ABC的高,CD=1,AD=
BD=3,则∠BAC的度数是75°或15°
下页
上页
考点专训
考点1锐角三角函数的意义
例1如图,在△ABC中,∠C=90°,AD是中线,
BD=4,AD=25,则tan∠CAD的值为(A)
A.2
B.√2
C.√3
D
例2(广州)在Rt△ABC中,∠C=90°,tanA
15
,BC=15,则AB=17
【点拨】解决此类问题要注意:(1)必须在直角三
角形中;(2)明确直角三角形边之间关系所表示
的锐角三角函数;(3)运用锐角三角函数求边长
或求三角函数值时常需结合勾股定理来解答.
考点2特殊角的三角函数值
例3(安徽)如图,O的半径为1,△ABC内接
于⊙O.若∠A=60°,∠B=75°,则AB=√2.
例4(广元改编)计算:2sin45°
1-2+(2020-x)+2sin60
解:原式=2Xy
2-4-(2-1)+1+2×3
解:在Rt△ABC中,∠C=90°,B1
an A
3……·∠A=30°,
∠ABC=60.∵BD是∠ABC的平分线
∴∠CBD=∠ABD=30°.又∵CD=√3
∴BC=CD
tan 30
在Rt△ABC中,∠C=90°,∠A=30°,
BO
∴AB
sin30°6
考点4解直角三角形的实际应用
例6(泰安)如图,为了测量
某建筑物BC的高度,小颖采
E D
用了如下的方法:先从与建筑
物底端B在同一水平线上的B
A点出发,沿斜坡AD行走130m至坡顶D处,
再从D处沿水平方向继续前行若干米后至点E
处,在E点测得该建筑物顶端C的仰角为60°,建
筑物底端B的俯角为45°,点A,B,C,D,E在同
平面内,斜坡AD的坡度i=1:2.4.根据小颖的
测量数据,计算出建筑物BC的高度约为(参考数
据:3≈1.732)
(A)
A.136.6m
B.86.7m
C.186.7m
D.86.6m
【点拨】利用解直角三角形知识解决实际问题的
关键是将实际问题转化为数学问题,选择或构造
合适的直角三角形进行求解
2.如图,在菱形ABCD中,DE⊥AB,cosA3
BE=2,则tan∠DBE的值为
(B)
A.1
(第2题图)
(第3题图)
3.如图,⊙O的直径AB垂直于弦CD于点E,
∠A=22.5°,OC=4,则CD的长为(C)
A.22B.4
C.4
D.8
4.如图,小明要测量河内小岛B到河边公路L的
距离,在A点测得∠BAD=30°,在C点测得
∠BCD=60°,又测得AC=50m,则小岛B到
公路l的距离为
(B)
A.25m
B
100√3
m
D.(25+253)m
B
C
D
B
(第4题图)
(第6题图)
5.(易错题)已知AD是△ABC的高,CD=1,AD=
BD=3,则∠BAC的度数是75°或15°
