【人教版】数学九年级下册 第28章 专题十二 求锐角三角函数的常用方法 习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 第28章 专题十二 求锐角三角函数的常用方法 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 639.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 15:06:38 | ||
图片预览





文档简介
(共16张PPT)
下页
上页
法指导
求锐角三角函数值需要谨记三角函数的基础条
件是直角三角形,所以有直角用好直角,没有直
角要构造直角,一般是通过作高来构造直角的,
如果不易构造适当的直角三角形,也可以通过等
角进行转化
专顶训练
类型1定义法
1.如图,平面直角坐标系中的点P的坐标为
(2,4),OP与x轴正半轴的夹角为a,则sina
的值为
(D)
/3
E
P
D
(第1题图)
(第2题图)
2.如图,在△ABC中,DE是BC的垂直平分线
DE交AC于点E,连接BE,若BE=9,BC
12,则cosC的值为
(B)
A
B
4
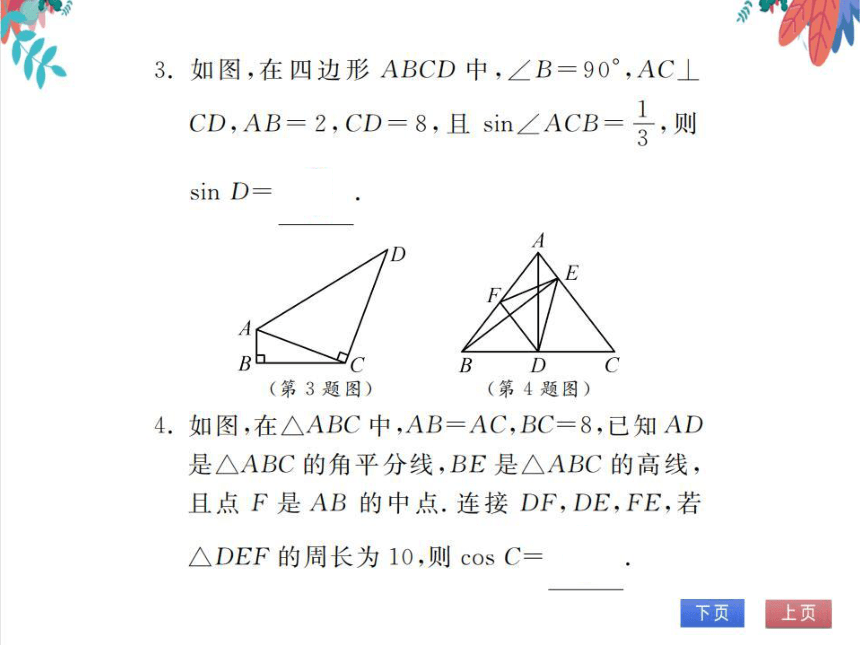
3.如图,在四边形ABCD中,∠B=90°,AC⊥
CD,AB=2,CD=8,且sin∠ACBl
则
D
B
(第3题图)
(第4题图)
4.如图,在△ABC中,AB=AC,BC=8,已知AD
是△ABC的角平分线,BE是△ABC的高线,
且点F是AB的中点.连接DF,DE,FE,若
△DEF的周长为10,则cosC=2
(1)BC的长;
(2)tan∠DAE的值
解:(1)∵AD是BC边
上的高,
∴∠ADB=∠ADC=90°.B
在Rt△ABD和Rt△ADC中,
∵ sin ral1
ab 3
,AD=1,AB=3.
∴BD=√AB2-AD=2√2
tan C-AD
AD
CD
即tan45
CD
∴AD=CD=1.∴BC=BD+CD=2√2+1
(2)∵AE是BC边上的中线,
BE I
BC=√2+
∴DE=BD-BE=_1
∴tan∠ DAE DE
AD
类型2巧设参数法
6.在R△ABC中,∠C=90°,mD_,那么
cOsA的值为
(B)
A
√5
2
B
D
7.如图,延长Rt△ABC的斜边AB到点D,使
BD=AB,连接CD,若tan∠BCD=1,则
3
tanA的值为
(A)
B.1
D
B
B
(第7题图
(第8题图)
9.如图,已知AD是等腰△ABC底边上的高,且
tan b-4
AC上有一点E,满足AE:CE
2:3,求tan∠ADE的值.
解:如图,过点E作EF⊥AD
于点F
∴△ABC是等腰三角形,
∴∠B=∠C
C
∴tanC=tanB≈AD4
CD 3
设AD=4k,则DC=3k,在Rt△ACD中,AC=5k
∵AE:CE=2:3,∴AE=2k,CE=3k.
EF⊥AD,AD为BC边上的高,∴EF∥CD
∴△AEF∽△ACD.· AF AE EF
AD AC CD
下页
上页
法指导
求锐角三角函数值需要谨记三角函数的基础条
件是直角三角形,所以有直角用好直角,没有直
角要构造直角,一般是通过作高来构造直角的,
如果不易构造适当的直角三角形,也可以通过等
角进行转化
专顶训练
类型1定义法
1.如图,平面直角坐标系中的点P的坐标为
(2,4),OP与x轴正半轴的夹角为a,则sina
的值为
(D)
/3
E
P
D
(第1题图)
(第2题图)
2.如图,在△ABC中,DE是BC的垂直平分线
DE交AC于点E,连接BE,若BE=9,BC
12,则cosC的值为
(B)
A
B
4
3.如图,在四边形ABCD中,∠B=90°,AC⊥
CD,AB=2,CD=8,且sin∠ACBl
则
D
B
(第3题图)
(第4题图)
4.如图,在△ABC中,AB=AC,BC=8,已知AD
是△ABC的角平分线,BE是△ABC的高线,
且点F是AB的中点.连接DF,DE,FE,若
△DEF的周长为10,则cosC=2
(1)BC的长;
(2)tan∠DAE的值
解:(1)∵AD是BC边
上的高,
∴∠ADB=∠ADC=90°.B
在Rt△ABD和Rt△ADC中,
∵ sin ral1
ab 3
,AD=1,AB=3.
∴BD=√AB2-AD=2√2
tan C-AD
AD
CD
即tan45
CD
∴AD=CD=1.∴BC=BD+CD=2√2+1
(2)∵AE是BC边上的中线,
BE I
BC=√2+
∴DE=BD-BE=_1
∴tan∠ DAE DE
AD
类型2巧设参数法
6.在R△ABC中,∠C=90°,mD_,那么
cOsA的值为
(B)
A
√5
2
B
D
7.如图,延长Rt△ABC的斜边AB到点D,使
BD=AB,连接CD,若tan∠BCD=1,则
3
tanA的值为
(A)
B.1
D
B
B
(第7题图
(第8题图)
9.如图,已知AD是等腰△ABC底边上的高,且
tan b-4
AC上有一点E,满足AE:CE
2:3,求tan∠ADE的值.
解:如图,过点E作EF⊥AD
于点F
∴△ABC是等腰三角形,
∴∠B=∠C
C
∴tanC=tanB≈AD4
CD 3
设AD=4k,则DC=3k,在Rt△ACD中,AC=5k
∵AE:CE=2:3,∴AE=2k,CE=3k.
EF⊥AD,AD为BC边上的高,∴EF∥CD
∴△AEF∽△ACD.· AF AE EF
AD AC CD
