【人教版】数学九年级下册 26.1.2.2第2课时 反比例函数的图像和性质(2)习题课件
文档属性
| 名称 | 【人教版】数学九年级下册 26.1.2.2第2课时 反比例函数的图像和性质(2)习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 829.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-01 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
00
下页
上页
下页上页
课前预习预习新知
k
1.过双曲线y=上的一点向两坐标轴作垂线,
与两坐标轴围成的矩形面积等于k;连
接该点与原点,还可得到两个直角三角形,它
们的面积分别为k
2.求两个函数的图象的交点坐标,就是把这两个
函数的解析式组成方程组并求解;利用函
数图象求不等式的解集,首先求出两图象的
交点坐标,再利用图象写出不等式的解集
当堂训练孔面基础
知识点1反比例函数中k的几何意义
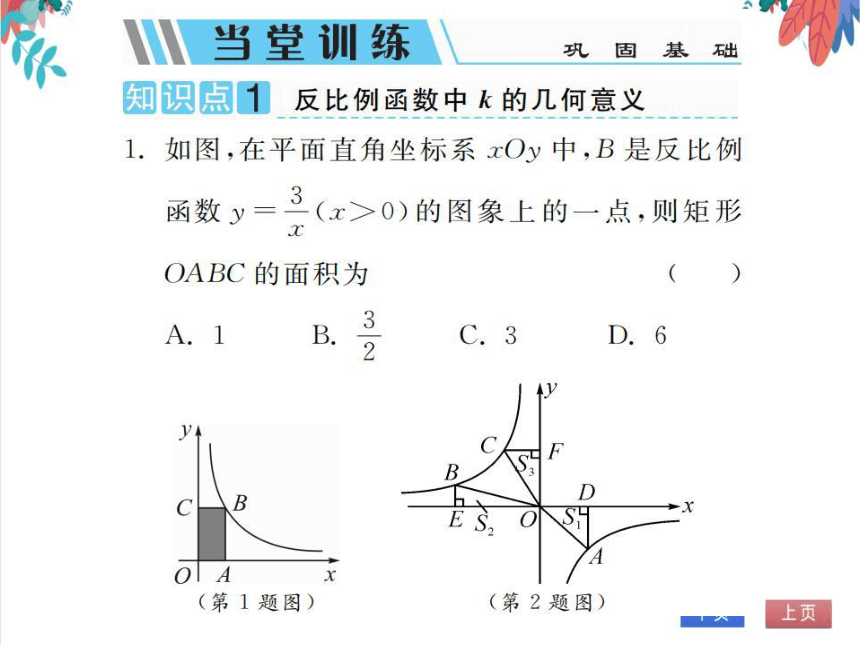
1.如图,在平面直角坐标系xOy中,B是反比例
函数y=-(x>0)的图象上的一点,则矩形
OABC的面积为
(C)
3
B
D.6
2
F
B
OI A
(第1题图)
(第2题图)
如图,在平面直角坐标系xOy中,反比例函数
k
的图象上有三点A,B,C,过点A作
AD⊥x轴于点D,过点B作BE⊥x轴于点
E,过点C作CF⊥y轴于点F,连接OA,OB,
OC,记△OAD,△OBE,△OCF的面积分别为
S1,S2,S3,则S1,S2和S3的大小关系为(C)
B.S1C. S
4.如图,反比例函数y=的图象经过点A(4,
b),过点A作AB⊥x轴于点B,△AOB的面
积为2
(1)求k和b的值;
(2)若一次函数y=ax-3的图象经过点A,求
这个一次函数的解析式
解:(1)∵反比例函数y
k
的
图象经过点A(4,b),AB⊥x
轴于点B,△AOB的面积为2,
OB·AB=2,即。×4·b=2
∴b=1.…∴A点的坐标为(4,1).∴k=xy=4.
k=4,b=
(2)∵A(4,1)在一次函数y=ax-3的图象
上,∴1=4a-3.∴a=1
∴这个一次函数的解析式为y=x-3
知识点2反比例函数图象与性质的综合运用
5.(天津)若点A(-5,y1),B(1,y2),C(5,y3)都
在反比例函数y
的图象上,则y,y2,y
的大小关系是
(B)
A. y1B. y2 C.y16.如图,正比例函数y1=k1x(k1<0)的图象与反
比例函数y2=(k2<0)的图象相交于A,B
两点,点B的横坐标为2,当y1>y2时,x的取
值范围是
(C)
或x>2
B.-22
C.x<-2或0D.-27.(龙东改编)已知反比例函数y=,当13时,y的最小整数值是3
00
下页
上页
下页上页
课前预习预习新知
k
1.过双曲线y=上的一点向两坐标轴作垂线,
与两坐标轴围成的矩形面积等于k;连
接该点与原点,还可得到两个直角三角形,它
们的面积分别为k
2.求两个函数的图象的交点坐标,就是把这两个
函数的解析式组成方程组并求解;利用函
数图象求不等式的解集,首先求出两图象的
交点坐标,再利用图象写出不等式的解集
当堂训练孔面基础
知识点1反比例函数中k的几何意义
1.如图,在平面直角坐标系xOy中,B是反比例
函数y=-(x>0)的图象上的一点,则矩形
OABC的面积为
(C)
3
B
D.6
2
F
B
OI A
(第1题图)
(第2题图)
如图,在平面直角坐标系xOy中,反比例函数
k
的图象上有三点A,B,C,过点A作
AD⊥x轴于点D,过点B作BE⊥x轴于点
E,过点C作CF⊥y轴于点F,连接OA,OB,
OC,记△OAD,△OBE,△OCF的面积分别为
S1,S2,S3,则S1,S2和S3的大小关系为(C)
B.S1
4.如图,反比例函数y=的图象经过点A(4,
b),过点A作AB⊥x轴于点B,△AOB的面
积为2
(1)求k和b的值;
(2)若一次函数y=ax-3的图象经过点A,求
这个一次函数的解析式
解:(1)∵反比例函数y
k
的
图象经过点A(4,b),AB⊥x
轴于点B,△AOB的面积为2,
OB·AB=2,即。×4·b=2
∴b=1.…∴A点的坐标为(4,1).∴k=xy=4.
k=4,b=
(2)∵A(4,1)在一次函数y=ax-3的图象
上,∴1=4a-3.∴a=1
∴这个一次函数的解析式为y=x-3
知识点2反比例函数图象与性质的综合运用
5.(天津)若点A(-5,y1),B(1,y2),C(5,y3)都
在反比例函数y
的图象上,则y,y2,y
的大小关系是
(B)
A. y1
比例函数y2=(k2<0)的图象相交于A,B
两点,点B的横坐标为2,当y1>y2时,x的取
值范围是
(C)
或x>2
B.-2
C.x<-2或0
