小学数学 人教版 五年级下册 4 分数的意义和性质 通分 最小公倍数的应用课件(21张PPT)
文档属性
| 名称 | 小学数学 人教版 五年级下册 4 分数的意义和性质 通分 最小公倍数的应用课件(21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 14:42:25 | ||
图片预览







文档简介
(共21张PPT)
人教版数学五年级(下)
第2课时 最小公倍数的应用
分数的意义和性质
4
5. 通分
1. 初步了解两个数的公倍数和最小公倍数在生活中的实际应用。
2. 培养独立思考、分析推理、自主提出问题和解决问题的能力。
3. 联系相关经验,激发学习数学的兴趣。
学习目标
【重点】
能够运用两个数的公倍数和最小公倍数的知识解决简单的实际问题。
【难点】
理解将实际问题转化成求两个数的公倍数问题的道理。
课堂导入
丁丁家装修时又遇到了一个问题,你能帮忙解决吗
新知探究
(教材第70页例3)
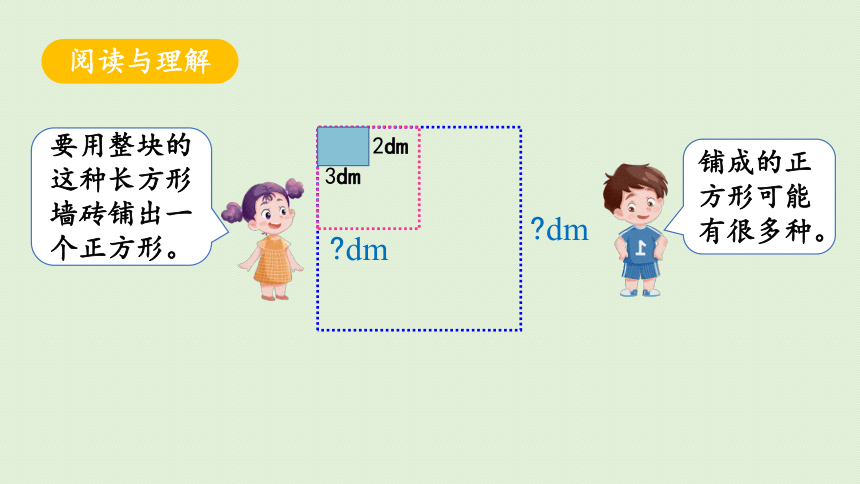
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
3
阅读与理解
你知道哪些信息?
3dm
2dm
dm
dm
边长可以是多少分米?
边长最小是多少分米?
3dm
2dm
dm
dm
3dm
2dm
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能有很多种。
阅读与理解
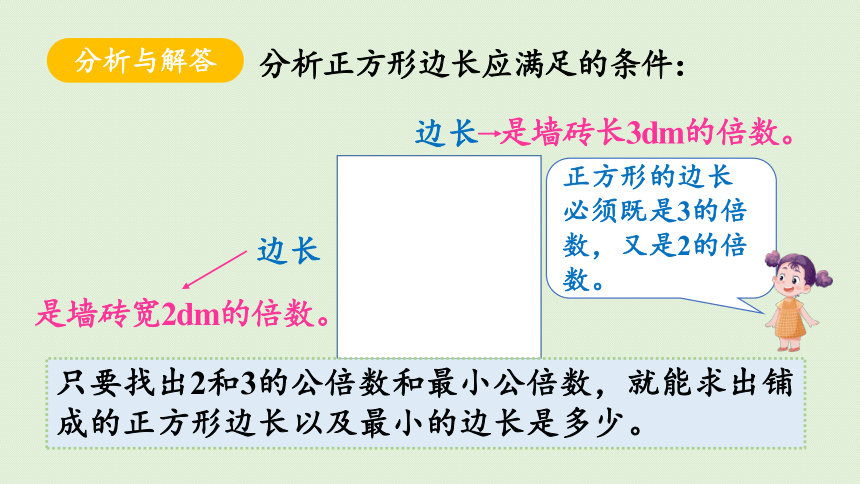
分析与解答
边长
是墙砖长3dm的倍数。
边长
是墙砖宽2dm的倍数。
分析正方形边长应满足的条件:
正方形的边长必须既是3的倍数,又是2的倍数。
只要找出2和3的公倍数和最小公倍数,就能求出铺成的正方形边长以及最小的边长是多少。
分析与解答
2的倍数有:2, 4, 6, 8, 10, 12, 14, 16, 18, …
3的倍数有:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6, 12, 18, …,最小公倍数是6。
所以,正方形的边长可以是6dm,12dm,18dm, …;边长最小是6dm。
回顾与反思
在边长6dm的正方形上画一画,看找得对不对。
可以画图来验证。
6 dm
6 dm
上边:6÷3=2(块)
3 dm
2 dm
左边:6÷2=3(块)
回顾与反思
在边长12dm的正方形上画一画,看找得对不对。
12 dm
12 dm
上边:12÷3=4(块)
左边:12÷2=6(块)
3 dm
2 dm
3
2和3的公倍数:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6 , 12, 18, …, 最小公倍数是6。
答:正方形的边长可以是6dm、12dm、18dm …,最小是6dm。
规范解答
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
回顾小结
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。要使用的墙砖必须都是整块,则铺成的正方形边长必须是墙砖长和宽的公倍数。要求最小的正方形边长就是求墙砖长与宽的最小公倍数。
当所求量分别与两个(或几个)已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
课堂练习
(教材第71页第6题)
同时浇水的时间必须是4和6的公倍数。
就是求4和6的最小公倍数。
4和6的公倍数有6,12,18,24,30,36, …
月季每 4 天浇一次水,君子兰每 6 天浇一次水。
1.
李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日
4和6的最小公倍数是12,5月1日过12天是5月13日。
答:下一次再给这两种花同时浇水应是5月13日。
(2)两个连续自然数的和是13,这两个数的最大公因数是( ),最小公倍数是( )。
(1)15和45的最大公因数是( ),最小公倍数是( )。
2. 填一填。
(3)如果a÷b=4(a、b为非0自然数),那么a与b的最大公因数是( ),最小公倍数是( ) 。
15
1
b
42
a
45
(2)75是15和25的( )。
A.倍数 B.公因数 C.最小公倍数
(1)两个数的( )是有限的。
A.公因数 B.公倍数 C.倍数
3. 选一选。
(3)甲数和乙数的差是1(甲、乙为非0自然数),它们的最小公倍数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
C
D
(教材第71页第7题)
就是求6和9在40以内的公倍数。
思路引导
先找出6和9 的公倍数,再与40人作比较。
4.
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
总人数必须是6和9的公倍数。
规范解答
4.
6和9的公倍数有9, 18, 27, 36, 45, 54,…
18<40, 36<40, 54>40, …
答:可能是18人或36人。
(教材第71页第7题)
提升练习
1. 甲、乙、丙为三个相咬合的齿轮,使甲轮转6圈时,乙轮转7圈,丙轮转2圈。这三个齿轮的齿数最少应分别是多少齿?
三个齿轮转过的总齿数是6、7、2的公倍数。
三个齿轮转过的总齿数也应最少。
6、7和2的最小公倍数是42。
6、7和2的公倍数有:7, 14, 21, 28, 35, 42, 49, …
甲轮齿数:42÷6=7(齿)
乙轮齿数:42÷7=6(齿)
丙轮齿数:42÷2=21(齿)
答:甲、乙、丙三个齿轮最少分别是7齿、6齿和21齿。
2 . A和B都是自然数,分解质因数得到A = 2 × 3 × a, B = 2 × 7 × a,如果A和B的最小公倍数是168,那么a等于多少?
思路引导
A = 2×3×a
A和B公有的质因数是2和a, A独有的质因数是3, B独有的质因数是7。
B = 2×7×a
最小公倍数=全部公有的质因数与各自独有质因数之积。
2×a×3×7=168
可以求出a的值
2 . A和B都是自然数,分解质因数得到A = 2 × 3 × a, B = 2 × 7 × a,如果A和B的最小公倍数是168,那么a等于多少?
规范解答
A = 2×3×a
B = 2×7×a
2×a×3×7 = 168
A和B的最小公倍数是
42a = 168
a = 4
答:a等于4。
课堂小结
同学们,这节课你们学会了哪些知识?
公倍数和最小公倍数的应用
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一时间到达问题等等。
人教版数学五年级(下)
第2课时 最小公倍数的应用
分数的意义和性质
4
5. 通分
1. 初步了解两个数的公倍数和最小公倍数在生活中的实际应用。
2. 培养独立思考、分析推理、自主提出问题和解决问题的能力。
3. 联系相关经验,激发学习数学的兴趣。
学习目标
【重点】
能够运用两个数的公倍数和最小公倍数的知识解决简单的实际问题。
【难点】
理解将实际问题转化成求两个数的公倍数问题的道理。
课堂导入
丁丁家装修时又遇到了一个问题,你能帮忙解决吗
新知探究
(教材第70页例3)
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
3
阅读与理解
你知道哪些信息?
3dm
2dm
dm
dm
边长可以是多少分米?
边长最小是多少分米?
3dm
2dm
dm
dm
3dm
2dm
要用整块的这种长方形墙砖铺出一个正方形。
铺成的正方形可能有很多种。
阅读与理解
分析与解答
边长
是墙砖长3dm的倍数。
边长
是墙砖宽2dm的倍数。
分析正方形边长应满足的条件:
正方形的边长必须既是3的倍数,又是2的倍数。
只要找出2和3的公倍数和最小公倍数,就能求出铺成的正方形边长以及最小的边长是多少。
分析与解答
2的倍数有:2, 4, 6, 8, 10, 12, 14, 16, 18, …
3的倍数有:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6, 12, 18, …,最小公倍数是6。
所以,正方形的边长可以是6dm,12dm,18dm, …;边长最小是6dm。
回顾与反思
在边长6dm的正方形上画一画,看找得对不对。
可以画图来验证。
6 dm
6 dm
上边:6÷3=2(块)
3 dm
2 dm
左边:6÷2=3(块)
回顾与反思
在边长12dm的正方形上画一画,看找得对不对。
12 dm
12 dm
上边:12÷3=4(块)
左边:12÷2=6(块)
3 dm
2 dm
3
2和3的公倍数:3, 6, 9, 12, 15, 18, …
2和3的公倍数有:6 , 12, 18, …, 最小公倍数是6。
答:正方形的边长可以是6dm、12dm、18dm …,最小是6dm。
规范解答
如果用这种墙砖铺一个正方形(用的墙砖必须都是整块),正方形的边长可以是多少分米?最小是多少分米?
回顾小结
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。要使用的墙砖必须都是整块,则铺成的正方形边长必须是墙砖长和宽的公倍数。要求最小的正方形边长就是求墙砖长与宽的最小公倍数。
当所求量分别与两个(或几个)已知量的倍数有关时,可以用公倍数或最小公倍数的知识解决。
课堂练习
(教材第71页第6题)
同时浇水的时间必须是4和6的公倍数。
就是求4和6的最小公倍数。
4和6的公倍数有6,12,18,24,30,36, …
月季每 4 天浇一次水,君子兰每 6 天浇一次水。
1.
李阿姨5月1日给月季和君子兰同时浇了水,下一次再给这两种花同时浇水应是5月几日
4和6的最小公倍数是12,5月1日过12天是5月13日。
答:下一次再给这两种花同时浇水应是5月13日。
(2)两个连续自然数的和是13,这两个数的最大公因数是( ),最小公倍数是( )。
(1)15和45的最大公因数是( ),最小公倍数是( )。
2. 填一填。
(3)如果a÷b=4(a、b为非0自然数),那么a与b的最大公因数是( ),最小公倍数是( ) 。
15
1
b
42
a
45
(2)75是15和25的( )。
A.倍数 B.公因数 C.最小公倍数
(1)两个数的( )是有限的。
A.公因数 B.公倍数 C.倍数
3. 选一选。
(3)甲数和乙数的差是1(甲、乙为非0自然数),它们的最小公倍数是( )。
A. 1 B. 甲 C. 乙 D. 甲、乙两数的积
A
C
D
(教材第71页第7题)
就是求6和9在40以内的公倍数。
思路引导
先找出6和9 的公倍数,再与40人作比较。
4.
如果这些学生的总人数在40人以内,可能是多少人?
咱们可以分成6人一组,也可以分成9人一组,都正好分完。
总人数必须是6和9的公倍数。
规范解答
4.
6和9的公倍数有9, 18, 27, 36, 45, 54,…
18<40, 36<40, 54>40, …
答:可能是18人或36人。
(教材第71页第7题)
提升练习
1. 甲、乙、丙为三个相咬合的齿轮,使甲轮转6圈时,乙轮转7圈,丙轮转2圈。这三个齿轮的齿数最少应分别是多少齿?
三个齿轮转过的总齿数是6、7、2的公倍数。
三个齿轮转过的总齿数也应最少。
6、7和2的最小公倍数是42。
6、7和2的公倍数有:7, 14, 21, 28, 35, 42, 49, …
甲轮齿数:42÷6=7(齿)
乙轮齿数:42÷7=6(齿)
丙轮齿数:42÷2=21(齿)
答:甲、乙、丙三个齿轮最少分别是7齿、6齿和21齿。
2 . A和B都是自然数,分解质因数得到A = 2 × 3 × a, B = 2 × 7 × a,如果A和B的最小公倍数是168,那么a等于多少?
思路引导
A = 2×3×a
A和B公有的质因数是2和a, A独有的质因数是3, B独有的质因数是7。
B = 2×7×a
最小公倍数=全部公有的质因数与各自独有质因数之积。
2×a×3×7=168
可以求出a的值
2 . A和B都是自然数,分解质因数得到A = 2 × 3 × a, B = 2 × 7 × a,如果A和B的最小公倍数是168,那么a等于多少?
规范解答
A = 2×3×a
B = 2×7×a
2×a×3×7 = 168
A和B的最小公倍数是
42a = 168
a = 4
答:a等于4。
课堂小结
同学们,这节课你们学会了哪些知识?
公倍数和最小公倍数的应用
解决墙砖铺正方形问题的关键是把铺砖问题转化为求公倍数的问题。利用公倍数和最小公倍数可以解决生活中的很多问题,如铺地砖问题、学生排队问题、同一时间到达问题等等。
