人教版数学九年级上册 24.2.2直线与圆的位置关系 (共18张)
文档属性
| 名称 | 人教版数学九年级上册 24.2.2直线与圆的位置关系 (共18张) |  | |
| 格式 | zip | ||
| 文件大小 | 302.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 20:32:58 | ||
图片预览




文档简介
(共18张PPT)
24.2.2直线与圆的
位置关系
在太阳升起过程中,太阳和地平线会有几种位置关系?
我们把太阳看作一个圆,地平线看作一条直线,由此你能看出它们经历了哪些过程吗?
观 察
地平线
.O
l
.O
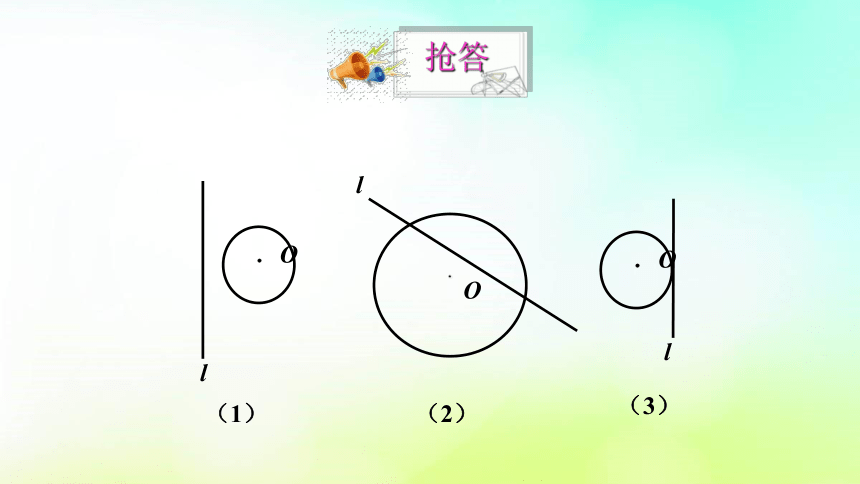
叫做直线和圆相离 .
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切 .
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交 .
这时的直线叫做圆的割线 .
直线和圆的位置关系
.A
.B
切点
割线
—— 用公共点的个数来区分
切线
这时的直线叫切线,
A
.O
l
.O
l
.
O
l
抢答
(1)
(2)
(3)
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线和圆的位置关系?
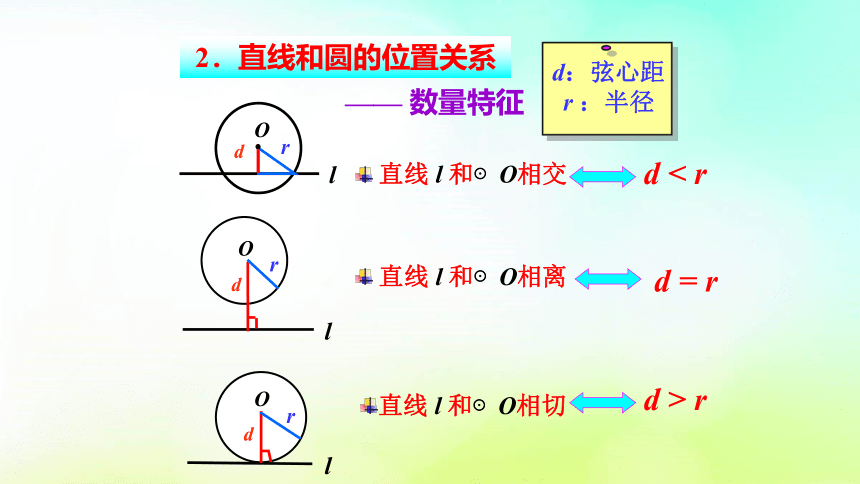
2.直线和圆的位置关系
—— 数量特征
r
d
直线 l 和⊙O相交
O
d
r
直线 l 和⊙O相离
d
r
直线 l 和⊙O相切
O
O
l
l
l
d < r
d = r
d > r
d:弦心距
r :半径
·
A
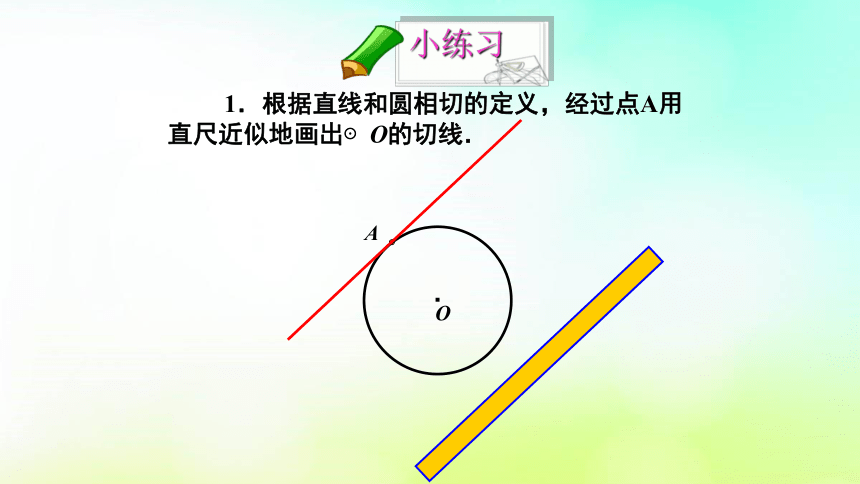
1.根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
O
小练习
2.圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线 与圆的公共点
圆心到直线的距离与半径
知识要点
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称 无
直线名称 无
课堂小结
相离
相切
相交
d < r
d = r
d > r
切点
交点
切线
割线
0
1
2
O
l
d
r
┐
┐
O
l
d
r
.
A
O
l
d
┐
r
C
B
.
.
1. 直线和圆的三种位置关系
.O
辨一辨
×
.C
1.若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
2.、直线与圆最多有两个公共
点 。…………………( )
√
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
2. 已知⊙O的直径是11cm,点O到直线a的距离是5.5cm,则⊙O与直线a的位置关系是 ______,直线a与⊙O的公共点个数是_______.
1. 已知⊙O的半径为5cm,点O到直线a的距离为3cm,则⊙O与直线a的位置关系是________;直线a与⊙O的公共点个数是_______.
相交
相切
两个
一个
随堂练习
3)若AB和⊙O相交,则 .
3、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
d > 5cm
d = 5cm
d < 5cm
0cm≤
4、直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
5.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与x 轴的位置关系是_____,⊙A与y 轴的位置关系是______。
相离
相切
O
X
Y
B
C
4
3
A
x
y
思考
例:圆的直径是12cm,如果圆心与直线的距离分别是
(1) r=4.5cm (2) r=6cm (3) r=8cm
那么直线和圆分别是什么位置关系?有几个公共点?
24.2.2直线与圆的
位置关系
在太阳升起过程中,太阳和地平线会有几种位置关系?
我们把太阳看作一个圆,地平线看作一条直线,由此你能看出它们经历了哪些过程吗?
观 察
地平线
.O
l
.O
叫做直线和圆相离 .
直线和圆没有公共点,
l
直线和圆有唯一的公共点,
叫做直线和圆相切 .
唯一的公共点叫切点.
.O
l
直线和圆有两个公共点,
叫做直线和圆相交 .
这时的直线叫做圆的割线 .
直线和圆的位置关系
.A
.B
切点
割线
—— 用公共点的个数来区分
切线
这时的直线叫切线,
A
.O
l
.O
l
.
O
l
抢答
(1)
(2)
(3)
除了用公共点的个数来区分直线与圆的位置关系外,能否像点和圆的位置关系一样用数量关系的方法来判断直线和圆的位置关系?
2.直线和圆的位置关系
—— 数量特征
r
d
直线 l 和⊙O相交
O
d
r
直线 l 和⊙O相离
d
r
直线 l 和⊙O相切
O
O
l
l
l
d < r
d = r
d > r
d:弦心距
r :半径
·
A
1.根据直线和圆相切的定义,经过点A用直尺近似地画出⊙O的切线.
O
小练习
2.圆的直径是13cm,如果直线与圆心的距离分别是
(1)4.5cm ; (2) 6.5cm ; (3) 8cm,
那么直线与圆分别是什么位置关系? 有几个公共点?
(3)圆心距 d=8cm>r = 6.5cm 直线与圆相离,
有两个公共点;
有一个公共点;
没有公共点.
A
B
·
6.5cm
d=4.5cm
O
M
(2)圆心距 d=6.5cm = r = 6.5cm 直线与圆相切,
·
N
O
6.5cm
d=6.5cm
解 (1) 圆心距 d=4.5cm< r = 6.5cm 直线与圆相交,
D
·
O
6.5cm
d=8cm
判定直线与圆的位置关系的方法有____种:
(1)根据定义,由__________________的个数来判断;
(2)根据性质,由_______________________的关系来判断.
(在实际应用中,常采用第二种方法判定)
两
直线 与圆的公共点
圆心到直线的距离与半径
知识要点
图形
直线与圆的位置关系
公共点的个数
圆心到直线的距离d与半径r的关系
公共点的名称 无
直线名称 无
课堂小结
相离
相切
相交
d < r
d = r
d > r
切点
交点
切线
割线
0
1
2
O
l
d
r
┐
┐
O
l
d
r
.
A
O
l
d
┐
r
C
B
.
.
1. 直线和圆的三种位置关系
.O
辨一辨
×
.C
1.若C为⊙O上的一点,则过点C的直线与⊙O相切。… … … …( )
2.、直线与圆最多有两个公共
点 。…………………( )
√
3 、若A、B是⊙O外两点, 则直线AB
与⊙O相离。… … … … …( )
×
.A1
.B1
.O
.A
.B
.B2
.A2
√
.
C
4、若C为⊙O内一点,则过点C的直线与⊙O相交。( )
.
O
2. 已知⊙O的直径是11cm,点O到直线a的距离是5.5cm,则⊙O与直线a的位置关系是 ______,直线a与⊙O的公共点个数是_______.
1. 已知⊙O的半径为5cm,点O到直线a的距离为3cm,则⊙O与直线a的位置关系是________;直线a与⊙O的公共点个数是_______.
相交
相切
两个
一个
随堂练习
3)若AB和⊙O相交,则 .
3、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d, 根据 条件填写d的范围:
1)若AB和⊙O相离, 则 ;
2)若AB和⊙O相切, 则 ;
d > 5cm
d = 5cm
d < 5cm
0cm≤
4、直线和圆有2个交点,则直线和圆_________;
直线和圆有1个交点,则直线和圆_________;
直线和圆有没有交点,则直线和圆_________;
相交
相切
相离
5.已知⊙A的直径为6,点A的坐标为(-3,-4),则⊙A与x 轴的位置关系是_____,⊙A与y 轴的位置关系是______。
相离
相切
O
X
Y
B
C
4
3
A
x
y
思考
例:圆的直径是12cm,如果圆心与直线的距离分别是
(1) r=4.5cm (2) r=6cm (3) r=8cm
那么直线和圆分别是什么位置关系?有几个公共点?
同课章节目录
