6.3.2 分数加减法的简便运算 课件(22张PPT)
文档属性
| 名称 | 6.3.2 分数加减法的简便运算 课件(22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-20 16:22:26 | ||
图片预览








文档简介
(共22张PPT)
人教版数学五年级(下)
分数的加法和减法
第2课时 分数加减法的简便运算
6
3. 分数加减混合运算
1. 理解整数加法的运算定律对分数加法同样适用,并能灵活运用加法运算定律进行简算;培养迁移、类推和归纳、概括的能力。
2. 养成用简明、灵活的方法解决问题的习惯。
3. 在探究的过程中体验成功的喜悦,提高对数学学习的兴趣。
学习目标
【重点】
正确应用加法运算定律进行简算。
【难点】
灵活运用运算定律进行简算。
课堂导入
怎样简便就怎样算。
478+156+122
1.95+1.4 +2.05+3.6
= 478+
= 600+156
= 1.95+
= 4 + 5
156
122
+
= 756
1.4
2.05
+
+3.6
(
)
(
)
= 9
说说各运用了什么运算定律?
加法交换律: a+b=b+a;
加法结合律:(a+b)+c=a+(b+c)
加法交换律
加法交换律和结合律
新知探究
2
先分别算算每组算式的得数?
教材第98页例2
下面每组算式的左右两边有什么样的关系?
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
7
2
3
7
+
=
7
5
7
3
2
7
+
=
7
5
=
4
1
+
4
3
2
3
+
(
)
=
12
9
11
12
+
=
20
12
=
3
5
4
1
+
4
3
2
3
+
(
)
=
1
2
3
+
=
3
5
=
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
=
=
调换到加号后
调换到加号前
=
3
7
2
7
调换了两个加数的位置,和不变。
(
)
①
②
①
②
=
改变了运算顺序,和不变。
加法交换律
加法结合律
发现:整数加法的交换律、结合律对分数加法同样适用。
2
下面每组算式的左右两边有什么样的关系?
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
=
=
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
算算看。
12
1
+
12
7
5
6
+
7
2
+
5
1
1
2
3
3
+
+
教材第98页例2
12
1
+
12
7
5
6
+
7
2
+
5
1
1
2
3
3
+
+
=
分母相同
12
1
+
12
7
5
6
+
(
)
运用加法结合律
=
6
4
5
6
+
灵活约分:
12
8
6
4
=
=
2
3
分母相同
=
3
2
+
7
2
1
1
3
5
+
+
运用加法交换律
=
35
10
+
35
7
1
+
(
)
运用加法结合律
=
35
17
1
发现:式子中有分母相同的分数,灵活地利用加法交换律、结合律先算,可以使计算简便。
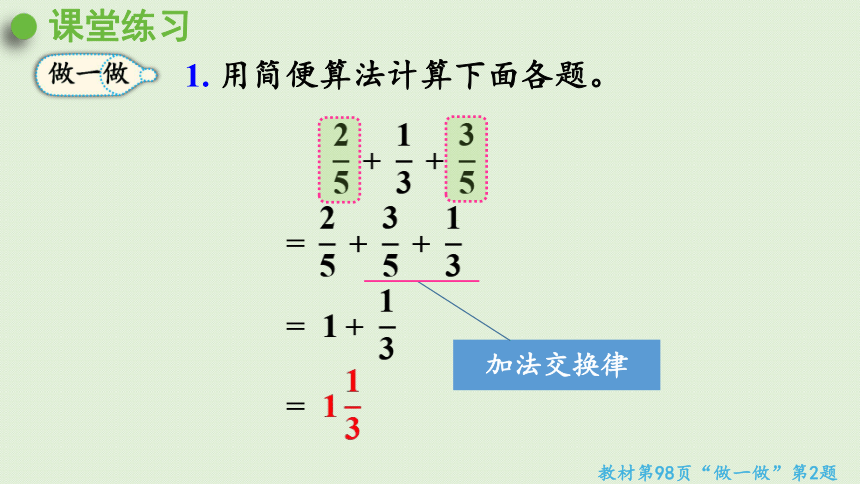
课堂练习
1. 用简便算法计算下面各题。
做一做
教材第98页“做一做”第2题
加法交换律
加法交换律和结合律
教材第98页“做一做”第2题
加法交换律和结合律
教材第98页“做一做”第2题
2. 把下面的算式填写完整。
(1)
6
1
2
1
3
6
+
=
+
(2)
7
5
2
3
( )
2
5
7
8
7
7
+
=
+
+
+
(3)
24
3
5
5
( )
5
3
5
24
12
24
24
12
-
=
-
-
○
(4)
11
3
6
7
( )
3
2
( )
11
9
11
9
+
=
+
+
+
+
+
2
3
3
8
6
11
7
9
2
9
+
加法交换律
加法结合律
加法交换律和结合律
连减的性质
3. 怎样简便怎样算。
4
1
这里可用连减的性质a–b–c=a-(b+c)进行简便。
胜利村修一条水渠,第一天修了 千米,第二天修了 千米,还剩 千米。这条水渠共长多少千米?
4.
9
2
9
7
5
2
水渠
9
2
km
5
2
km
9
7
km
?km
5
2
+
9
7
2
9
+
=
9
7
+
5
2
2
9
+
=
5
2
1
(km)
答:这条水渠共长 千米。
5
2
1
运用加法交换律
拓展提升
4
1
+
8
1
1
1
1
2
16
32
+
+
+
思路一
先通分,再计算:
1. 求 的值。
4
1
+
8
1
1
1
1
2
16
32
+
+
+
=
32
8
+
32
4
16
2
1
32
32
32
+
+
+
=
32
16+8+4+2+1
=
32
31
拓展提升
4
1
+
8
1
1
1
1
2
16
32
+
+
+
思路二
先画图,找规律,再计算:
1. 求 的值。
2
1
4
1
8
1
16
1
32
1
32
1
从图中可以看出:涂色部分的和就是 的值。所以,算式的值等于“1”减去剩下的空白部分,即1- 。
4
1
+
8
1
1
1
1
2
16
32
+
+
+
32
1
4
1
+
8
1
1
1
1
2
16
32
+
+
+
=
1 -
32
1
=
32
31
拓展延伸
4
1
+
8
1
1
1
1
1
2
16
1024
2048
+
+
+
+
+
…
求 的值。
4
1
+
8
1
1
1
1
1
2
16
1024
2048
+
+
+
+
+
…
=
1 -
2048
1
=
2048
2047
请认准算式的特征:一个连加算式,第一个加数是 ,之后每个加数的分母是前一个加数分母的2倍,且分子都是1。
2
1
用你的发现计算下面这道题。
6
1
+
12
1
1
1
2
20
+
+
你能发现什么?
思路引导
计算并发现规律:
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
2.
教材第101页第8*题
1-
2
1
2
1
=
2
1
3
1
( )
( )
-
=
3
1
4
1
( )
( )
-
=
4
1
5
1
( )
( )
-
=
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
分母是原来两分母的积
分子是原来两分母的差
分母为相邻的两个自然数,差为1。
6
1
+
12
1
1
1
2
20
+
+
1-
2
1
=
+
1
2
1
3
-
+
1
3
1
4
-
+
1
4
1
5
-
=
1-
5
1
4
5
=
应用规律
1×2
2×3
3×4
4×5
互相抵消
教材第101页第8*题
课堂小结
同学们,这节课你们学会了哪些知识?
分数加减法的简便运算:
(1)整数加法的交换律、结合律对分数加法同样适用。
(2)灵活地运用运算定律,可以使一些分数计算简便。
人教版数学五年级(下)
分数的加法和减法
第2课时 分数加减法的简便运算
6
3. 分数加减混合运算
1. 理解整数加法的运算定律对分数加法同样适用,并能灵活运用加法运算定律进行简算;培养迁移、类推和归纳、概括的能力。
2. 养成用简明、灵活的方法解决问题的习惯。
3. 在探究的过程中体验成功的喜悦,提高对数学学习的兴趣。
学习目标
【重点】
正确应用加法运算定律进行简算。
【难点】
灵活运用运算定律进行简算。
课堂导入
怎样简便就怎样算。
478+156+122
1.95+1.4 +2.05+3.6
= 478+
= 600+156
= 1.95+
= 4 + 5
156
122
+
= 756
1.4
2.05
+
+3.6
(
)
(
)
= 9
说说各运用了什么运算定律?
加法交换律: a+b=b+a;
加法结合律:(a+b)+c=a+(b+c)
加法交换律
加法交换律和结合律
新知探究
2
先分别算算每组算式的得数?
教材第98页例2
下面每组算式的左右两边有什么样的关系?
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
7
2
3
7
+
=
7
5
7
3
2
7
+
=
7
5
=
4
1
+
4
3
2
3
+
(
)
=
12
9
11
12
+
=
20
12
=
3
5
4
1
+
4
3
2
3
+
(
)
=
1
2
3
+
=
3
5
=
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
=
=
调换到加号后
调换到加号前
=
3
7
2
7
调换了两个加数的位置,和不变。
(
)
①
②
①
②
=
改变了运算顺序,和不变。
加法交换律
加法结合律
发现:整数加法的交换律、结合律对分数加法同样适用。
2
下面每组算式的左右两边有什么样的关系?
7
2
○
7
2
3
3
7
7
+
+
4
1
1
4
+
4
3
2
2
3
3
3
4
+
○
+
+
(
)
(
)
=
=
整数加法的交换律、结合律对分数加法同样适用。利用运算定律可以使一些分数计算变得简便。
算算看。
12
1
+
12
7
5
6
+
7
2
+
5
1
1
2
3
3
+
+
教材第98页例2
12
1
+
12
7
5
6
+
7
2
+
5
1
1
2
3
3
+
+
=
分母相同
12
1
+
12
7
5
6
+
(
)
运用加法结合律
=
6
4
5
6
+
灵活约分:
12
8
6
4
=
=
2
3
分母相同
=
3
2
+
7
2
1
1
3
5
+
+
运用加法交换律
=
35
10
+
35
7
1
+
(
)
运用加法结合律
=
35
17
1
发现:式子中有分母相同的分数,灵活地利用加法交换律、结合律先算,可以使计算简便。
课堂练习
1. 用简便算法计算下面各题。
做一做
教材第98页“做一做”第2题
加法交换律
加法交换律和结合律
教材第98页“做一做”第2题
加法交换律和结合律
教材第98页“做一做”第2题
2. 把下面的算式填写完整。
(1)
6
1
2
1
3
6
+
=
+
(2)
7
5
2
3
( )
2
5
7
8
7
7
+
=
+
+
+
(3)
24
3
5
5
( )
5
3
5
24
12
24
24
12
-
=
-
-
○
(4)
11
3
6
7
( )
3
2
( )
11
9
11
9
+
=
+
+
+
+
+
2
3
3
8
6
11
7
9
2
9
+
加法交换律
加法结合律
加法交换律和结合律
连减的性质
3. 怎样简便怎样算。
4
1
这里可用连减的性质a–b–c=a-(b+c)进行简便。
胜利村修一条水渠,第一天修了 千米,第二天修了 千米,还剩 千米。这条水渠共长多少千米?
4.
9
2
9
7
5
2
水渠
9
2
km
5
2
km
9
7
km
?km
5
2
+
9
7
2
9
+
=
9
7
+
5
2
2
9
+
=
5
2
1
(km)
答:这条水渠共长 千米。
5
2
1
运用加法交换律
拓展提升
4
1
+
8
1
1
1
1
2
16
32
+
+
+
思路一
先通分,再计算:
1. 求 的值。
4
1
+
8
1
1
1
1
2
16
32
+
+
+
=
32
8
+
32
4
16
2
1
32
32
32
+
+
+
=
32
16+8+4+2+1
=
32
31
拓展提升
4
1
+
8
1
1
1
1
2
16
32
+
+
+
思路二
先画图,找规律,再计算:
1. 求 的值。
2
1
4
1
8
1
16
1
32
1
32
1
从图中可以看出:涂色部分的和就是 的值。所以,算式的值等于“1”减去剩下的空白部分,即1- 。
4
1
+
8
1
1
1
1
2
16
32
+
+
+
32
1
4
1
+
8
1
1
1
1
2
16
32
+
+
+
=
1 -
32
1
=
32
31
拓展延伸
4
1
+
8
1
1
1
1
1
2
16
1024
2048
+
+
+
+
+
…
求 的值。
4
1
+
8
1
1
1
1
1
2
16
1024
2048
+
+
+
+
+
…
=
1 -
2048
1
=
2048
2047
请认准算式的特征:一个连加算式,第一个加数是 ,之后每个加数的分母是前一个加数分母的2倍,且分子都是1。
2
1
用你的发现计算下面这道题。
6
1
+
12
1
1
1
2
20
+
+
你能发现什么?
思路引导
计算并发现规律:
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
2.
教材第101页第8*题
1-
2
1
2
1
=
2
1
3
1
( )
( )
-
=
3
1
4
1
( )
( )
-
=
4
1
5
1
( )
( )
-
=
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
1-
2
1
=
1
1
1
2
-
=
2-1
1×2
1
2
=
1
2
1
3
-
=
3-2
2×3
1
6
=
1
3
1
4
-
=
4-3
3×4
1
12
=
1
4
1
5
-
=
5-4
4×5
1
20
=
分母是原来两分母的积
分子是原来两分母的差
分母为相邻的两个自然数,差为1。
6
1
+
12
1
1
1
2
20
+
+
1-
2
1
=
+
1
2
1
3
-
+
1
3
1
4
-
+
1
4
1
5
-
=
1-
5
1
4
5
=
应用规律
1×2
2×3
3×4
4×5
互相抵消
教材第101页第8*题
课堂小结
同学们,这节课你们学会了哪些知识?
分数加减法的简便运算:
(1)整数加法的交换律、结合律对分数加法同样适用。
(2)灵活地运用运算定律,可以使一些分数计算简便。
