☆综合实践活动——打电话课件(22张PPT)
文档属性
| 名称 | ☆综合实践活动——打电话课件(22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
人教版数学五年级(下)
综合实践活动
打 电 话
1. 从解决问题的多种方案中寻找“打电话”的最优方案,发现事物隐含的规律。
2. 通过画图、表格等多种方式,自主探究、合作交流,培养归纳推理和应用数学知识解决实际问题的能力。体会数形结合、推理、优化、模型等数学思想。
3. 进一步体验数学与生活的密切联系以及优化思想在生活中的应用。
活动目标
【重点】
探究和理解“打电话”的最优方法及隐含的规律。
【难点】
探究和理解“打电话”的最优方法中隐含的规律。
请你提取这个实际问题的关键信息,写在下面。
要通知的人数: ;
通知的方式及用时: ;
对于通知的要求: 。
情境导入
一个合唱队共有 15 人,暑假期间有一个紧急演出,老师需要尽快通知到每一个队员。如果用打电话的方式,每分钟通知 1 人,请帮助老师设计一个打电话的方案。
15 人
打电话,每分钟通知1人
尽快通知到每一个队员
活动过程
可以一个一个地通知。
这样太慢了……
师
生1
生2
生3
……
生13
生14
生15
思路引导
你打算怎么解决呢?
一共需要15分钟
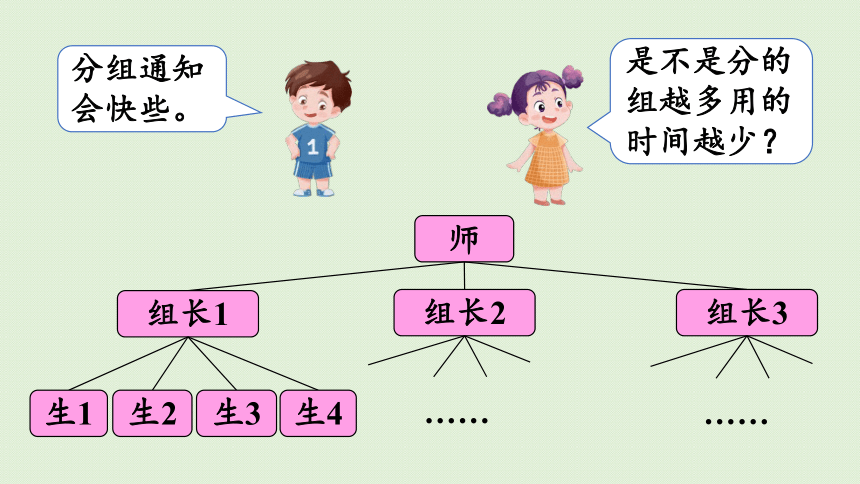
分组通知会快些。
师
组长1
生1
生2
生3
生4
组长2
……
组长3
……
是不是分的组越多用的时间越少?
想一想:还有更快的方法吗?
每个队员接到通知后马上通知别人。
接下来他(她)再继续通知其他人……
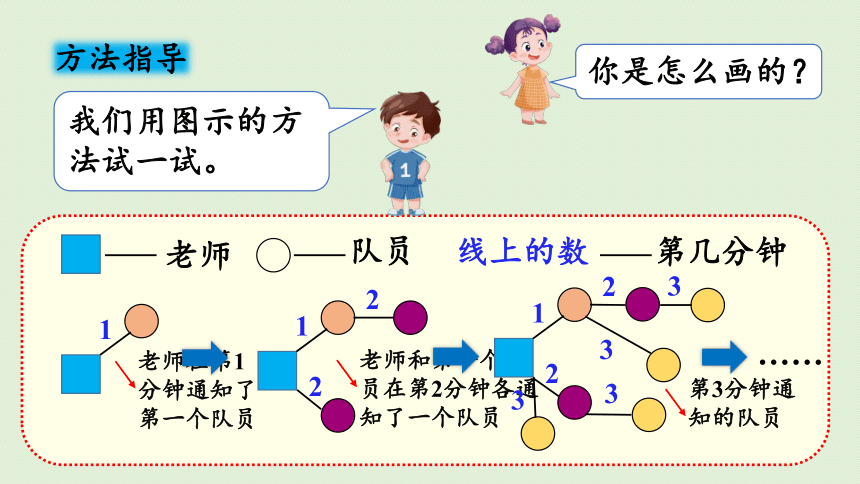
方法指导
我们用图示的方法试一试。
老师
队员
线上的数
第几分钟
1
老师在第1分钟通知了第一个队员
1
2
2
老师和第一个队员在第2分钟各通知了一个队员
1
2
2
3
3
3
3
……
第3分钟通知的队员
你是怎么画的?
小组合作:探究最省时的打电话方案。
合作要求
1.选一种方案在组内进行具体探讨,找出最优方案(可用画示意图、列表等)。
2.回顾研究过程,看其中有没有什么规律。
3.小结本组的发现,准备全班汇报。
发现规律
我们组探讨了分组通知方案。
(1)把15个队员分成3组,每组5人,每组设1个组长。老师先通知各组长,组长再通知组内其他4个队员。
师
组长1
生1
生2
生3
生4
组长2
……
组长3
……
生11
生12
①
②
③
②
③
③
④
④
④
⑤
⑤
⑤
⑥
⑥
⑦
共需要7分钟
发现规律
我们组探讨了分组通知方案。
(2)把15个队员分成4组,前3组每组4人,最后一组3人,每组设1个组长。老师先通知各组长,组长再通知组内其他队员。
师
组长1
生1
生2
生3
①
②
③
②
③
④
共需要6分钟
组长4
组长2
生5
生6
③
④
⑤
生4
组长3
生8
生9
④
⑥
生7
⑤
④
生10
生11
⑤
⑥
发现规律
我们组探讨了分组通知方案。
(3)把15个队员分成5组,每组3人,每组设1个组长。老师先通知各组长,组长再通知组内其他队员。
师
组长1
生1
生2
①
②
④
②
③
共需要7分钟
组长5
⑤
生9
生10
⑥
⑦
③
组长2
生3
生4
③
④
组长3
生5
生6
④
⑤
组长4
生7
生8
⑤
⑥
发现规律
我们组探讨了分组通知方案。
我们发现:并不是分的组越多,所用的时间就越少。
我们的结论:采用分组通知的方案,分4组最省时间。
上述方案好像总有人闲着哟!
发现规律
我们组探讨了全员参与通知方案。
老师依次通知4个队员,每个队员接到通知后马上再通知其他队员(不重复通知)。
1
2
2
3
3
3
3
4
4
4
4
4
4
4
我们的结论:采用全员参与通知的方案4分钟就可通知到每个人。
我们发现:每轮通知都没有空闲的人,所以花的时间最少。
4
发现规律
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
1
3
7
15
31
63
127
…
…
…
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
128
-1
-1
-1
-1
-1
-1
-1
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
128
1
3
7
15
31
63
127
…
…
…
×2
×2
×2
×2
×2
×2
每增加1分钟,新接到通知的队员数正好是前面所有接到通知的队员和老师的总数。
到第n分钟所有接到通知的队员和老师的总数是前(n-1)分钟所有接到通知的队员和老师总数的2倍。
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
128
1
3
7
15
31
63
127
…
…
…
4=2×2
8=2×2×2
16=2×2×2×2
2个2相乘
3个2相乘
4个2相乘
…
到第n分钟,所有接到通知的队员和老师的总数是n个2相乘的积;
所有接到通知的队员总数是n个2相乘的积-1。
-1
-1
-1
-1
应用规律
1. 按上面的方式,5分钟最多可以通知多少人?
方法一:推理法
到4分钟已经通知了15人,第6分钟,一共有16人在打电话,可以通知16人,所以最多可以通知15+16=31(人)。
方法二:计算法
到第5分钟,所有接到通知的总人数是5个2相乘的积-1,即2×2×2×2×2-1=32-1=31(人)。
2. 如果一个合唱团有50人,最多花多长时间就能通知
到每个人?
方法一:推理法
到5分钟已经通知了31人, 第6分钟, 一共有32人在打电话,可以通知32人, 所以最多可以通知31+32=63(人),
63>50,所以最少花6分钟就能通知到每个人。
方法二:计算法
到第5分钟,2×2×2×2×2-1=32-1=31(人);到第6分钟,2×2×2×2×2×2-1=64-1=63(人)。
31<50<63,所以最少花6分钟就能通知到每个人。
回顾与反思
设计最优方案时,我用到了图示的方法。
我用到了列表的方法。
我用到了对比分析的方法。
1. 回顾整个过程,你用到了哪些方法?
回顾反思
先画好电话通知的示意图。
再确定谁通知谁。
2. 你制订的方案在现实中可行吗?为使它切实可行,
还需要做些什么?
保证每个队员接到通知后都不闲着。
还得清楚接到电话后该继续通知谁。
活动小结
同学们,通过这次活动你有哪些收获?
探究“打电话”的最优方案:
(1)用图示的方法先画出电话通知的示意图,确定谁通知谁。
(2)保证每个人接到电话后都不闲着,且清楚自己要继续通知哪些人。
(3)到第n分钟,所有接到通知的队员总数是n个2相乘的积-1。
人教版数学五年级(下)
综合实践活动
打 电 话
1. 从解决问题的多种方案中寻找“打电话”的最优方案,发现事物隐含的规律。
2. 通过画图、表格等多种方式,自主探究、合作交流,培养归纳推理和应用数学知识解决实际问题的能力。体会数形结合、推理、优化、模型等数学思想。
3. 进一步体验数学与生活的密切联系以及优化思想在生活中的应用。
活动目标
【重点】
探究和理解“打电话”的最优方法及隐含的规律。
【难点】
探究和理解“打电话”的最优方法中隐含的规律。
请你提取这个实际问题的关键信息,写在下面。
要通知的人数: ;
通知的方式及用时: ;
对于通知的要求: 。
情境导入
一个合唱队共有 15 人,暑假期间有一个紧急演出,老师需要尽快通知到每一个队员。如果用打电话的方式,每分钟通知 1 人,请帮助老师设计一个打电话的方案。
15 人
打电话,每分钟通知1人
尽快通知到每一个队员
活动过程
可以一个一个地通知。
这样太慢了……
师
生1
生2
生3
……
生13
生14
生15
思路引导
你打算怎么解决呢?
一共需要15分钟
分组通知会快些。
师
组长1
生1
生2
生3
生4
组长2
……
组长3
……
是不是分的组越多用的时间越少?
想一想:还有更快的方法吗?
每个队员接到通知后马上通知别人。
接下来他(她)再继续通知其他人……
方法指导
我们用图示的方法试一试。
老师
队员
线上的数
第几分钟
1
老师在第1分钟通知了第一个队员
1
2
2
老师和第一个队员在第2分钟各通知了一个队员
1
2
2
3
3
3
3
……
第3分钟通知的队员
你是怎么画的?
小组合作:探究最省时的打电话方案。
合作要求
1.选一种方案在组内进行具体探讨,找出最优方案(可用画示意图、列表等)。
2.回顾研究过程,看其中有没有什么规律。
3.小结本组的发现,准备全班汇报。
发现规律
我们组探讨了分组通知方案。
(1)把15个队员分成3组,每组5人,每组设1个组长。老师先通知各组长,组长再通知组内其他4个队员。
师
组长1
生1
生2
生3
生4
组长2
……
组长3
……
生11
生12
①
②
③
②
③
③
④
④
④
⑤
⑤
⑤
⑥
⑥
⑦
共需要7分钟
发现规律
我们组探讨了分组通知方案。
(2)把15个队员分成4组,前3组每组4人,最后一组3人,每组设1个组长。老师先通知各组长,组长再通知组内其他队员。
师
组长1
生1
生2
生3
①
②
③
②
③
④
共需要6分钟
组长4
组长2
生5
生6
③
④
⑤
生4
组长3
生8
生9
④
⑥
生7
⑤
④
生10
生11
⑤
⑥
发现规律
我们组探讨了分组通知方案。
(3)把15个队员分成5组,每组3人,每组设1个组长。老师先通知各组长,组长再通知组内其他队员。
师
组长1
生1
生2
①
②
④
②
③
共需要7分钟
组长5
⑤
生9
生10
⑥
⑦
③
组长2
生3
生4
③
④
组长3
生5
生6
④
⑤
组长4
生7
生8
⑤
⑥
发现规律
我们组探讨了分组通知方案。
我们发现:并不是分的组越多,所用的时间就越少。
我们的结论:采用分组通知的方案,分4组最省时间。
上述方案好像总有人闲着哟!
发现规律
我们组探讨了全员参与通知方案。
老师依次通知4个队员,每个队员接到通知后马上再通知其他队员(不重复通知)。
1
2
2
3
3
3
3
4
4
4
4
4
4
4
我们的结论:采用全员参与通知的方案4分钟就可通知到每个人。
我们发现:每轮通知都没有空闲的人,所以花的时间最少。
4
发现规律
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
1
3
7
15
31
63
127
…
…
…
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
×2
128
-1
-1
-1
-1
-1
-1
-1
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
128
1
3
7
15
31
63
127
…
…
…
×2
×2
×2
×2
×2
×2
每增加1分钟,新接到通知的队员数正好是前面所有接到通知的队员和老师的总数。
到第n分钟所有接到通知的队员和老师的总数是前(n-1)分钟所有接到通知的队员和老师总数的2倍。
第n分钟 1 2 3 4 5 6 7 …
第n分钟新接到通知 的人数
到第n分钟所有接到通知 的队员和老师的总数
到第n分钟所有接到通知 的队员总数
1
2
4
8
16
32
64
2
4
8
16
32
64
128
1
3
7
15
31
63
127
…
…
…
4=2×2
8=2×2×2
16=2×2×2×2
2个2相乘
3个2相乘
4个2相乘
…
到第n分钟,所有接到通知的队员和老师的总数是n个2相乘的积;
所有接到通知的队员总数是n个2相乘的积-1。
-1
-1
-1
-1
应用规律
1. 按上面的方式,5分钟最多可以通知多少人?
方法一:推理法
到4分钟已经通知了15人,第6分钟,一共有16人在打电话,可以通知16人,所以最多可以通知15+16=31(人)。
方法二:计算法
到第5分钟,所有接到通知的总人数是5个2相乘的积-1,即2×2×2×2×2-1=32-1=31(人)。
2. 如果一个合唱团有50人,最多花多长时间就能通知
到每个人?
方法一:推理法
到5分钟已经通知了31人, 第6分钟, 一共有32人在打电话,可以通知32人, 所以最多可以通知31+32=63(人),
63>50,所以最少花6分钟就能通知到每个人。
方法二:计算法
到第5分钟,2×2×2×2×2-1=32-1=31(人);到第6分钟,2×2×2×2×2×2-1=64-1=63(人)。
31<50<63,所以最少花6分钟就能通知到每个人。
回顾与反思
设计最优方案时,我用到了图示的方法。
我用到了列表的方法。
我用到了对比分析的方法。
1. 回顾整个过程,你用到了哪些方法?
回顾反思
先画好电话通知的示意图。
再确定谁通知谁。
2. 你制订的方案在现实中可行吗?为使它切实可行,
还需要做些什么?
保证每个队员接到通知后都不闲着。
还得清楚接到电话后该继续通知谁。
活动小结
同学们,通过这次活动你有哪些收获?
探究“打电话”的最优方案:
(1)用图示的方法先画出电话通知的示意图,确定谁通知谁。
(2)保证每个人接到电话后都不闲着,且清楚自己要继续通知哪些人。
(3)到第n分钟,所有接到通知的队员总数是n个2相乘的积-1。
