人教版 五年级下册数学 6.3.3 用分数加减法解决问题课件 (共24张PPT)
文档属性
| 名称 | 人教版 五年级下册数学 6.3.3 用分数加减法解决问题课件 (共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 20:15:19 | ||
图片预览



文档简介
(共24张PPT)
人教版数学五年级(下)
第3课时 用分数加减法解决问题
分数的加法和减法
6
3. 分数加减混合运算
1. 体会图示在理解问题、分析和解决问题中的作用,学习用几何直观分析、解决问题的策略。
2. 经历问题解决的全过程,探索解决问题的途径、策略和方法。
3. 感受数学知识与日常生活的联系,养成用简明、灵活的方法解决问题的习惯。
学习目标
【重点】
分析数量关系,运用几何直观解决问题。
【难点】
掌握运用几何直观解决问题的策略。
课堂导入
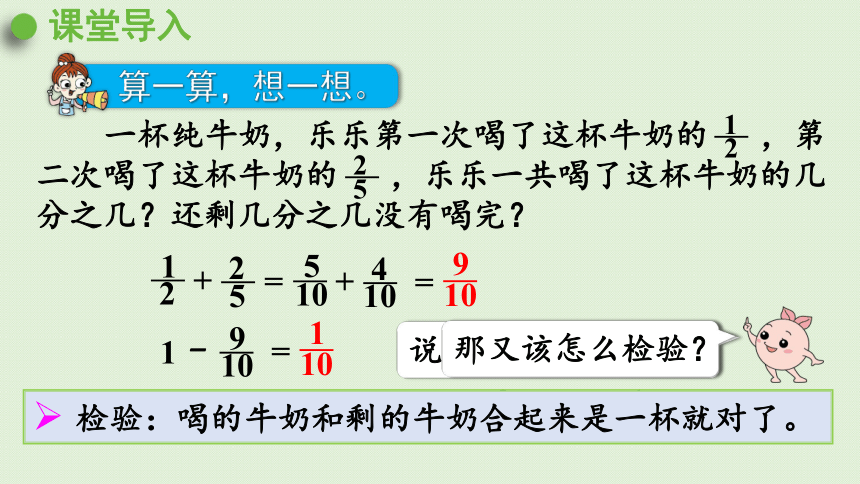
算一算,想一想。
一杯纯牛奶,乐乐第一次喝了这杯牛奶的 ,第二次喝了这杯牛奶的 ,乐乐一共喝了这杯牛奶的几分之几?还剩几分之几没有喝完?
2
1
5
2
2
1
5
2
+
=
10
5
10
4
+
=
10
9
1
10
9
-
=
10
1
答:乐乐一共喝了这杯牛奶的 ,还剩 没有喝完。
10
9
10
1
说说你是怎么想的?
检验:喝的牛奶和剩的牛奶合起来是一杯就对了。
那又该怎么检验?
新知探究
3
教材第99页例3
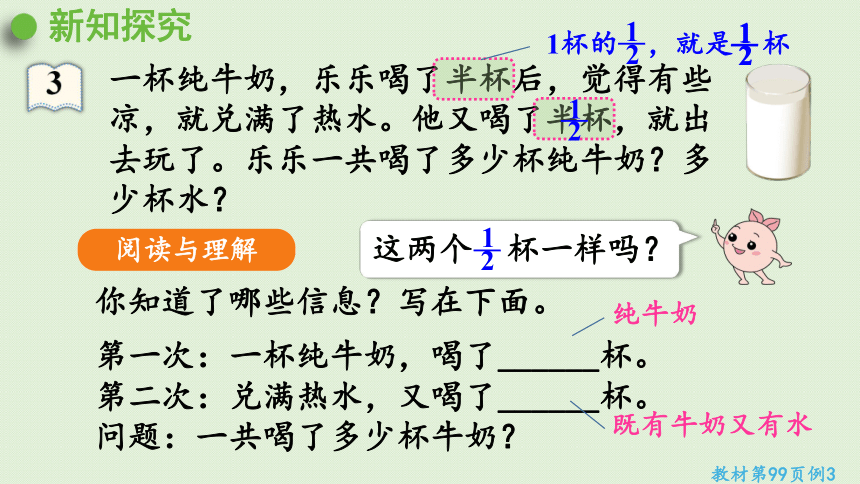
一杯纯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水。他又喝了半杯,就出去玩了。乐乐一共喝了多少杯纯牛奶?多少杯水?
阅读与理解
你知道了哪些信息?写在下面。
第一次:一杯纯牛奶,喝了______杯。
第二次:兑满热水,又喝了______杯。
问题:一共喝了多少杯牛奶?
1杯的 ,就是 杯
2
1
2
1
2
1
2
1
这两个 杯一样吗?
2
1
纯牛奶
既有牛奶又有水
分析与解答
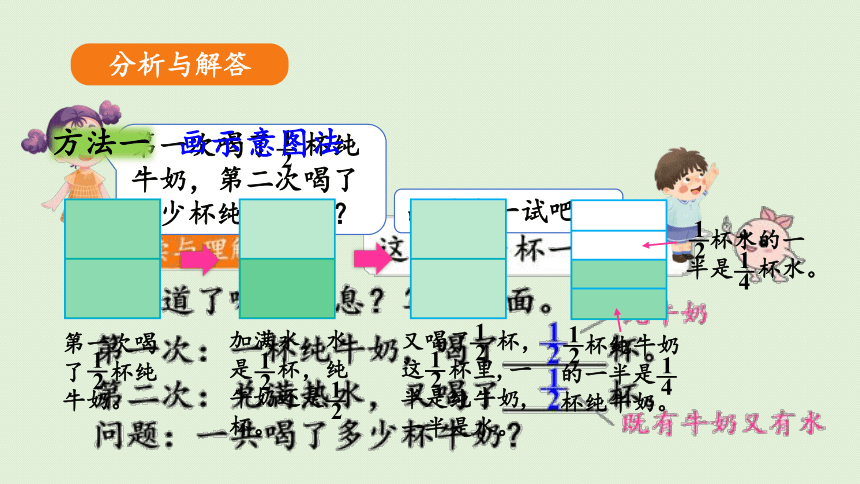
第一次喝了 杯纯牛奶,第二次喝了多少杯纯牛奶呢?
2
1
画图试一试吧。
第一次喝了 杯纯牛奶。
2
1
加满水,水是 杯,纯牛奶还是 杯。
2
1
2
1
又喝了 杯,这 杯里,一半是纯牛奶,一半是水。
2
1
2
1
杯纯牛奶的一半是 杯纯牛奶。
4
1
2
1
杯水的一半是 杯水。
4
1
2
1
方法一
画示意图法
分析与解答
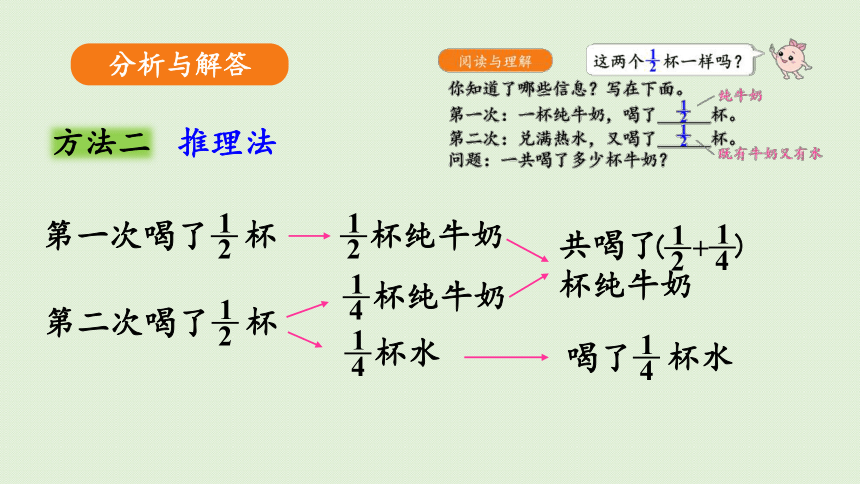
第一次喝了 杯
1
2
杯纯牛奶
1
2
第二次喝了 杯
1
2
杯纯牛奶
1
4
杯水
1
4
共喝了
杯纯牛奶
1
2
1
4
+
(
)
喝了 杯水
1
4
方法二
推理法
分析与解答
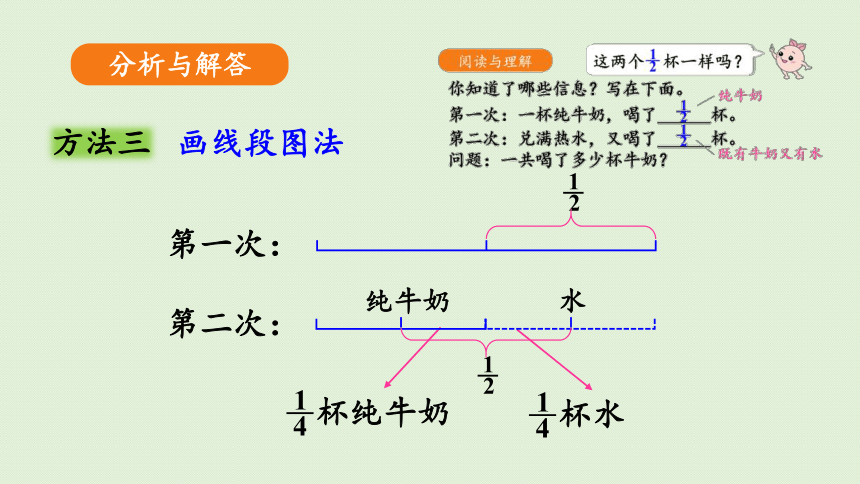
第一次:
杯纯牛奶
1
4
杯水
1
4
方法三
画线段图法
1
2
第二次:
纯牛奶
水
1
2
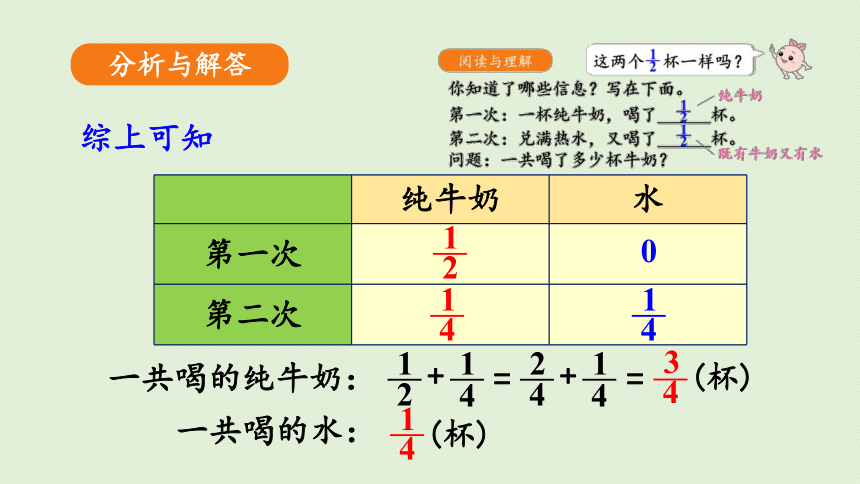
分析与解答
综上可知
纯牛奶 水
第一次
第二次
1
2
1
4
1
4
0
一共喝的纯牛奶:
1
2
1
4
+
=
3
4
(杯)
2
4
1
4
+
=
一共喝的水:
1
4
(杯)
回顾与反思
可以怎样检验?
检验
喝掉的加剩下的是否等于原来的。
杯
1
2
杯
1
4
第一次
纯牛奶
第二次
杯
1
4
4
1
+
4
1
1
2
+
1
(杯)
=
4
1
+
4
1
2
4
+
=
一杯纯牛奶
两次喝掉的纯牛奶和剩下的纯牛奶合起来正好是1杯,说明解答正确。
回顾与反思
可以怎样检验?
检验
喝掉的加剩下的是否等于原来的。
杯
1
2
杯
1
4
第一次
纯牛奶
第二次
杯
1
4
4
1
+
4
1
1
2
+
1
(杯)
=
4
1
+
4
1
2
4
+
=
一杯纯牛奶
答:乐乐一共喝了 杯纯牛奶, 杯水。
4
3
4
1
回顾与反思
解决这道题的关键是什么?
解决这道题的关键是要知道第二次喝了一杯纯牛奶的几分之几,也就是解决 杯纯牛奶的一半是多少。
2
1
水
奶
把 平均分成2份,就是把“1”平均分成4份,其中的1份就是 。
2
1
4
1
回顾与反思
关键步骤利用了什么知识?
在解决问题的关键步骤上,利用了画图法来分析理解题目的含义,灵活的运用了分数的意义,分数的加减法,画图法等知识点。
课堂练习
1. 用你喜欢的方式画一画,涂一涂,表示出下列算式和结果。
1
8
3
8
+
1
2
1
3
+
8
1
8
3
2
1
=
2
1
3
1
6
5
=
答案不唯一
2. 一瓶果汁,明明分四次喝完。第一次喝了这瓶果汁的 ,然后加满水,第二次喝了一瓶的 ,再加满水,第三次喝了半瓶,又加满水,第四次一饮而尽。明明喝的果汁多还是水多?你是怎样想的?
3
1
6
1
阅读与理解
你知道了哪些信息?
次数 喝了多少 加水多少
第一次
第二次
第三次
第四次
6
1
6
1
3
1
3
1
2
1
2
1
1
0
分析与解答
从表中可知:虽然明明每次喝的不一样多,但最后是一饮而尽的,所以他喝的果汁总共是 1 瓶,这是不变的。
分析与解答
从表中可知:虽然明明每次喝的不一样多,但最后是一饮而尽的,所以他和的果汁总共是 1 瓶,这是不变的。
先考虑明明喝果汁的量
分析与解答
再考虑明明喝水的量
从表中可知:明明三次加水的量分别是这瓶果汁的 ,
和 ,所以喝水的总量是
6
1
3
1
2
1
5
1
+
9
1
1
6
+
= 1(瓶)。
分析与解答
比较明明喝的果汁和水量
从上面的分析计算中可知,明明喝的果汁和水都是1 瓶。说明他喝的果汁和水同样多。
2. 一瓶果汁,明明分四次喝完。第一次喝了这瓶果汁的 ,然后加满水,第二次喝了一瓶的 ,再加满水,第三次喝了半瓶,又加满水,第四次一饮而尽。明明喝的果汁多还是水多?你是怎样想的?
3
1
6
1
规范解答
一共喝的果汁:
1
6
1
3
+
+
1
2
=
=
一共喝的水:
1
(瓶)
1
6
2
6
+
+
3
6
1
(瓶)
答:明明喝的果汁和水同样多。
拓展提升
思路引导
先考虑每个图形的面积各占几分之几
观察题图容易发现:图形1和图形2的面积各占正方形的 。剩下的图形面积与正方形面积的关系的判断有一定困难,可添加辅助线帮助理解。
4
1
教材第101页思考题
图形 1 2 3 4 5 6 7
面积(占正方形的几分之几)
每个图形的面积占正方形的几分之几见下表:
4
1
4
1
16
1
8
1
16
1
8
1
8
1
教材第101页思考题
图形 1 2 3 4 5 6 7
面积(占正方形的几分之几)
每个图形的面积占正方形的几分之几见下表:
4
1
4
1
16
1
8
1
16
1
8
1
8
1
教材第101页思考题
再求图形7和4,图形3、4、5共占几分之几。
图形7和4:
1
8
1
8
+
4
1
=
图形3、4、5:
1
16
1
8
+
+
1
16
=
1
16
2
16
+
+
1
16
4
1
=
课堂小结
同学们,这节课你们学会了哪些知识?
分数加减法的实际运用:
解决喝牛奶(或果汁)问题的关键是要先确定喝的次数,弄清每次喝的牛奶和水分别是多少;借助几何直观(画图)可以帮助我们分析数量关系,从而解决问题。
人教版数学五年级(下)
第3课时 用分数加减法解决问题
分数的加法和减法
6
3. 分数加减混合运算
1. 体会图示在理解问题、分析和解决问题中的作用,学习用几何直观分析、解决问题的策略。
2. 经历问题解决的全过程,探索解决问题的途径、策略和方法。
3. 感受数学知识与日常生活的联系,养成用简明、灵活的方法解决问题的习惯。
学习目标
【重点】
分析数量关系,运用几何直观解决问题。
【难点】
掌握运用几何直观解决问题的策略。
课堂导入
算一算,想一想。
一杯纯牛奶,乐乐第一次喝了这杯牛奶的 ,第二次喝了这杯牛奶的 ,乐乐一共喝了这杯牛奶的几分之几?还剩几分之几没有喝完?
2
1
5
2
2
1
5
2
+
=
10
5
10
4
+
=
10
9
1
10
9
-
=
10
1
答:乐乐一共喝了这杯牛奶的 ,还剩 没有喝完。
10
9
10
1
说说你是怎么想的?
检验:喝的牛奶和剩的牛奶合起来是一杯就对了。
那又该怎么检验?
新知探究
3
教材第99页例3
一杯纯牛奶,乐乐喝了半杯后,觉得有些凉,就兑满了热水。他又喝了半杯,就出去玩了。乐乐一共喝了多少杯纯牛奶?多少杯水?
阅读与理解
你知道了哪些信息?写在下面。
第一次:一杯纯牛奶,喝了______杯。
第二次:兑满热水,又喝了______杯。
问题:一共喝了多少杯牛奶?
1杯的 ,就是 杯
2
1
2
1
2
1
2
1
这两个 杯一样吗?
2
1
纯牛奶
既有牛奶又有水
分析与解答
第一次喝了 杯纯牛奶,第二次喝了多少杯纯牛奶呢?
2
1
画图试一试吧。
第一次喝了 杯纯牛奶。
2
1
加满水,水是 杯,纯牛奶还是 杯。
2
1
2
1
又喝了 杯,这 杯里,一半是纯牛奶,一半是水。
2
1
2
1
杯纯牛奶的一半是 杯纯牛奶。
4
1
2
1
杯水的一半是 杯水。
4
1
2
1
方法一
画示意图法
分析与解答
第一次喝了 杯
1
2
杯纯牛奶
1
2
第二次喝了 杯
1
2
杯纯牛奶
1
4
杯水
1
4
共喝了
杯纯牛奶
1
2
1
4
+
(
)
喝了 杯水
1
4
方法二
推理法
分析与解答
第一次:
杯纯牛奶
1
4
杯水
1
4
方法三
画线段图法
1
2
第二次:
纯牛奶
水
1
2
分析与解答
综上可知
纯牛奶 水
第一次
第二次
1
2
1
4
1
4
0
一共喝的纯牛奶:
1
2
1
4
+
=
3
4
(杯)
2
4
1
4
+
=
一共喝的水:
1
4
(杯)
回顾与反思
可以怎样检验?
检验
喝掉的加剩下的是否等于原来的。
杯
1
2
杯
1
4
第一次
纯牛奶
第二次
杯
1
4
4
1
+
4
1
1
2
+
1
(杯)
=
4
1
+
4
1
2
4
+
=
一杯纯牛奶
两次喝掉的纯牛奶和剩下的纯牛奶合起来正好是1杯,说明解答正确。
回顾与反思
可以怎样检验?
检验
喝掉的加剩下的是否等于原来的。
杯
1
2
杯
1
4
第一次
纯牛奶
第二次
杯
1
4
4
1
+
4
1
1
2
+
1
(杯)
=
4
1
+
4
1
2
4
+
=
一杯纯牛奶
答:乐乐一共喝了 杯纯牛奶, 杯水。
4
3
4
1
回顾与反思
解决这道题的关键是什么?
解决这道题的关键是要知道第二次喝了一杯纯牛奶的几分之几,也就是解决 杯纯牛奶的一半是多少。
2
1
水
奶
把 平均分成2份,就是把“1”平均分成4份,其中的1份就是 。
2
1
4
1
回顾与反思
关键步骤利用了什么知识?
在解决问题的关键步骤上,利用了画图法来分析理解题目的含义,灵活的运用了分数的意义,分数的加减法,画图法等知识点。
课堂练习
1. 用你喜欢的方式画一画,涂一涂,表示出下列算式和结果。
1
8
3
8
+
1
2
1
3
+
8
1
8
3
2
1
=
2
1
3
1
6
5
=
答案不唯一
2. 一瓶果汁,明明分四次喝完。第一次喝了这瓶果汁的 ,然后加满水,第二次喝了一瓶的 ,再加满水,第三次喝了半瓶,又加满水,第四次一饮而尽。明明喝的果汁多还是水多?你是怎样想的?
3
1
6
1
阅读与理解
你知道了哪些信息?
次数 喝了多少 加水多少
第一次
第二次
第三次
第四次
6
1
6
1
3
1
3
1
2
1
2
1
1
0
分析与解答
从表中可知:虽然明明每次喝的不一样多,但最后是一饮而尽的,所以他喝的果汁总共是 1 瓶,这是不变的。
分析与解答
从表中可知:虽然明明每次喝的不一样多,但最后是一饮而尽的,所以他和的果汁总共是 1 瓶,这是不变的。
先考虑明明喝果汁的量
分析与解答
再考虑明明喝水的量
从表中可知:明明三次加水的量分别是这瓶果汁的 ,
和 ,所以喝水的总量是
6
1
3
1
2
1
5
1
+
9
1
1
6
+
= 1(瓶)。
分析与解答
比较明明喝的果汁和水量
从上面的分析计算中可知,明明喝的果汁和水都是1 瓶。说明他喝的果汁和水同样多。
2. 一瓶果汁,明明分四次喝完。第一次喝了这瓶果汁的 ,然后加满水,第二次喝了一瓶的 ,再加满水,第三次喝了半瓶,又加满水,第四次一饮而尽。明明喝的果汁多还是水多?你是怎样想的?
3
1
6
1
规范解答
一共喝的果汁:
1
6
1
3
+
+
1
2
=
=
一共喝的水:
1
(瓶)
1
6
2
6
+
+
3
6
1
(瓶)
答:明明喝的果汁和水同样多。
拓展提升
思路引导
先考虑每个图形的面积各占几分之几
观察题图容易发现:图形1和图形2的面积各占正方形的 。剩下的图形面积与正方形面积的关系的判断有一定困难,可添加辅助线帮助理解。
4
1
教材第101页思考题
图形 1 2 3 4 5 6 7
面积(占正方形的几分之几)
每个图形的面积占正方形的几分之几见下表:
4
1
4
1
16
1
8
1
16
1
8
1
8
1
教材第101页思考题
图形 1 2 3 4 5 6 7
面积(占正方形的几分之几)
每个图形的面积占正方形的几分之几见下表:
4
1
4
1
16
1
8
1
16
1
8
1
8
1
教材第101页思考题
再求图形7和4,图形3、4、5共占几分之几。
图形7和4:
1
8
1
8
+
4
1
=
图形3、4、5:
1
16
1
8
+
+
1
16
=
1
16
2
16
+
+
1
16
4
1
=
课堂小结
同学们,这节课你们学会了哪些知识?
分数加减法的实际运用:
解决喝牛奶(或果汁)问题的关键是要先确定喝的次数,弄清每次喝的牛奶和水分别是多少;借助几何直观(画图)可以帮助我们分析数量关系,从而解决问题。
