八年级数学等腰三角形的性质
文档属性
| 名称 | 八年级数学等腰三角形的性质 |  | |
| 格式 | zip | ||
| 文件大小 | 239.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-23 16:40:39 | ||
图片预览


文档简介
课件26张PPT。九年级数学(上册)第一章 证明(二)1.你能证明它们吗(2)
等腰三角形的性质、判定这两个三角形的关系是——全等三角形全等的判定方法我们学过那些判定方法?SSS、SAS、ASA几何的三种语言公理:
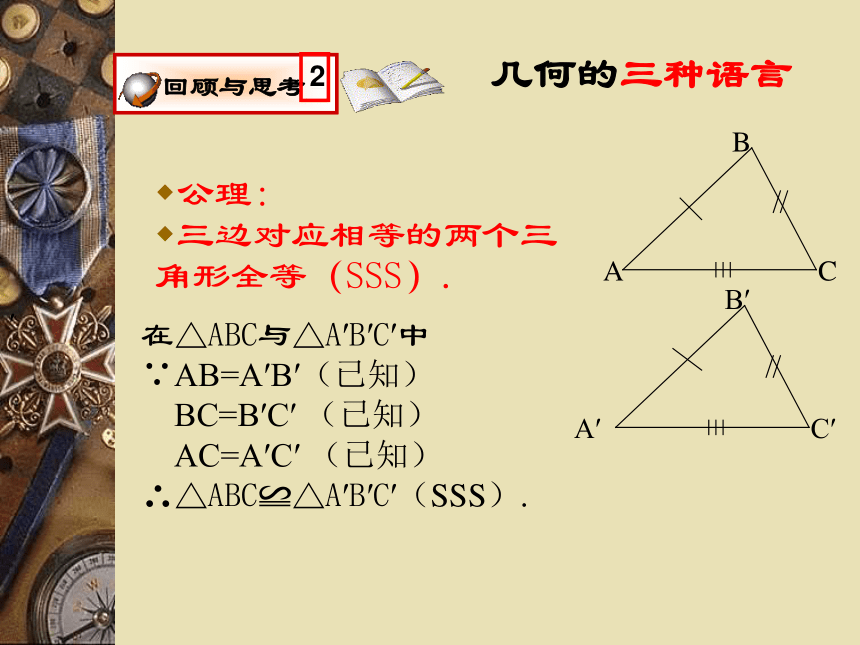
三边对应相等的两个三角形全等(SSS).在△ABC与△A′B′C′中
∵AB=A′B′(已知)
BC=B′C′ (已知)
AC=A′C′ (已知)∴△ABC≌△A′B′C′(SSS).′几何的三种语言公理:
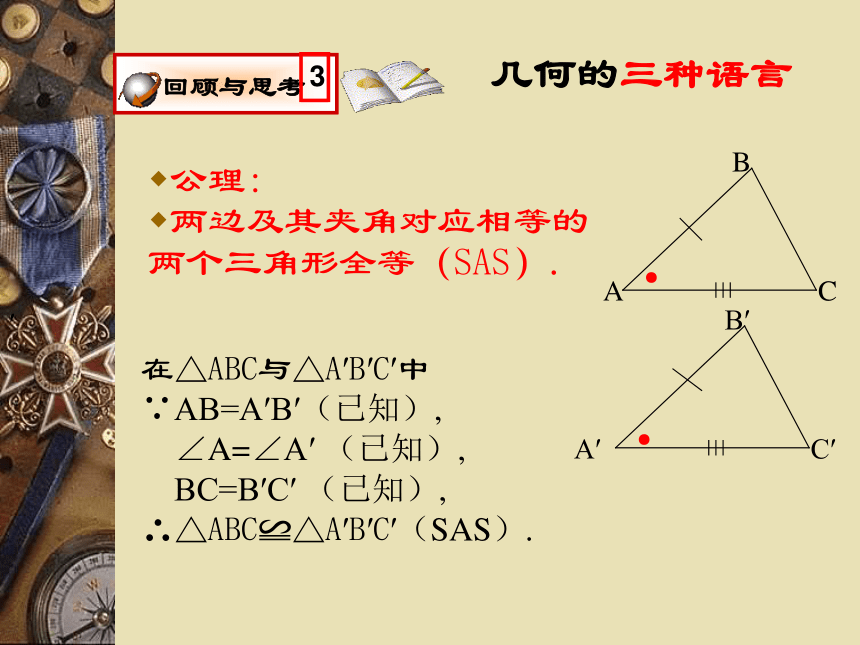
两边及其夹角对应相等的两个三角形全等(SAS).在△ABC与△A′B′C′中
∵AB=A′B′(已知),
∠A=∠A′ (已知),
BC=B′C′ (已知),
∴△ABC≌△A′B′C′(SAS).′几何的三种语言公理:
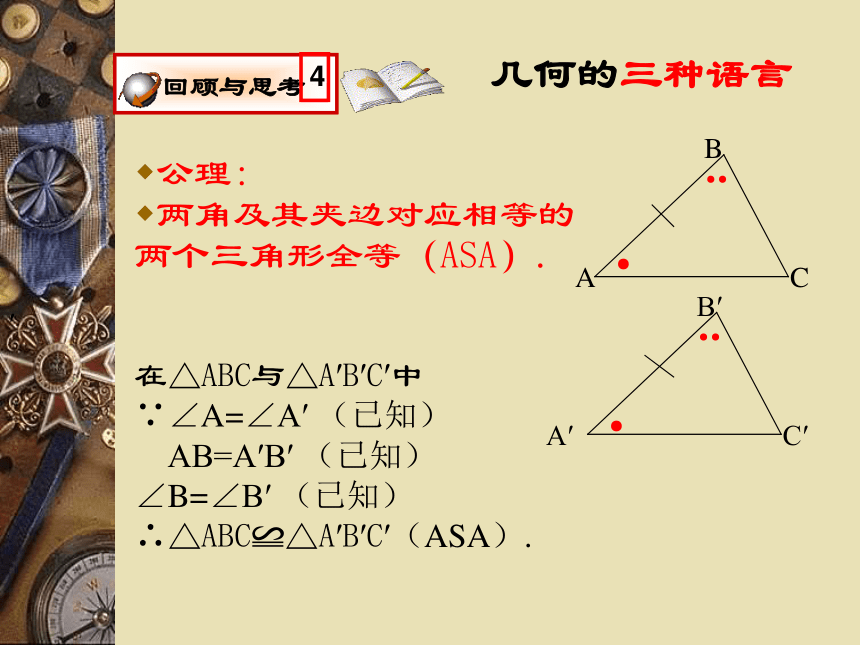
两角及其夹边对应相等的两个三角形全等(ASA).在△ABC与△A′B′C′中
∵∠A=∠A′ (已知)
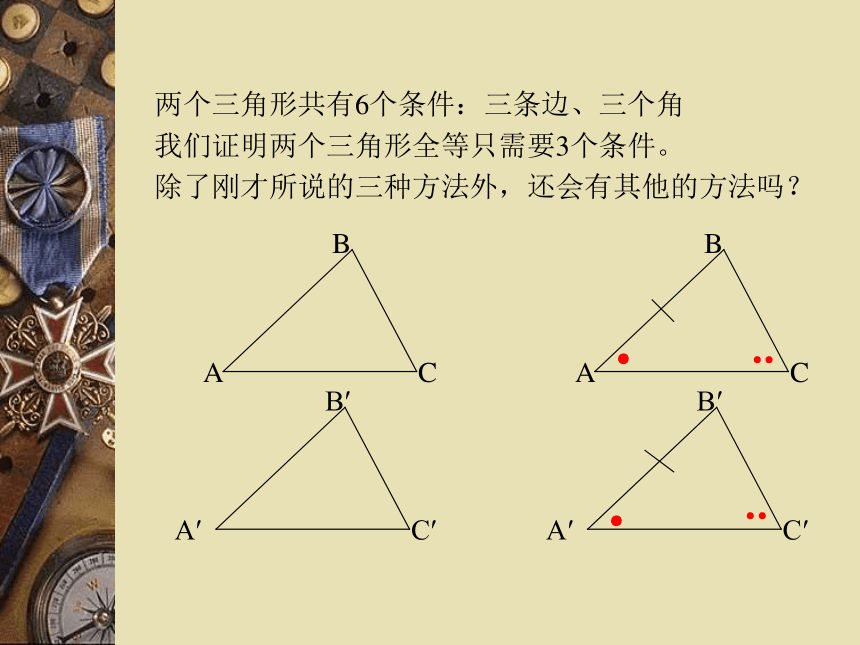
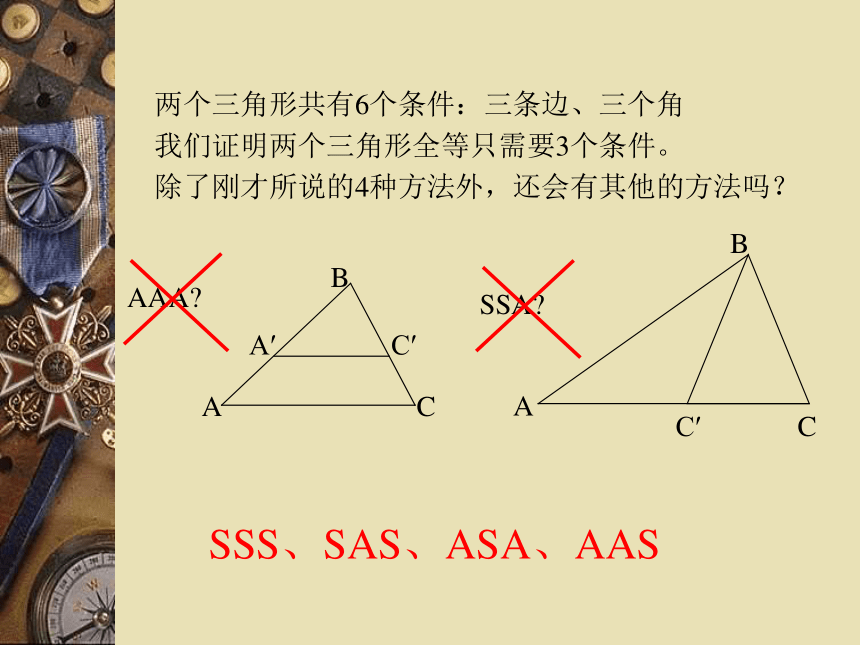
AB=A′B′ (已知) ∠B=∠B′ (已知) ∴△ABC≌△A′B′C′(ASA).′两个三角形共有6个条件:三条边、三个角
我们证明两个三角形全等只需要3个条件。
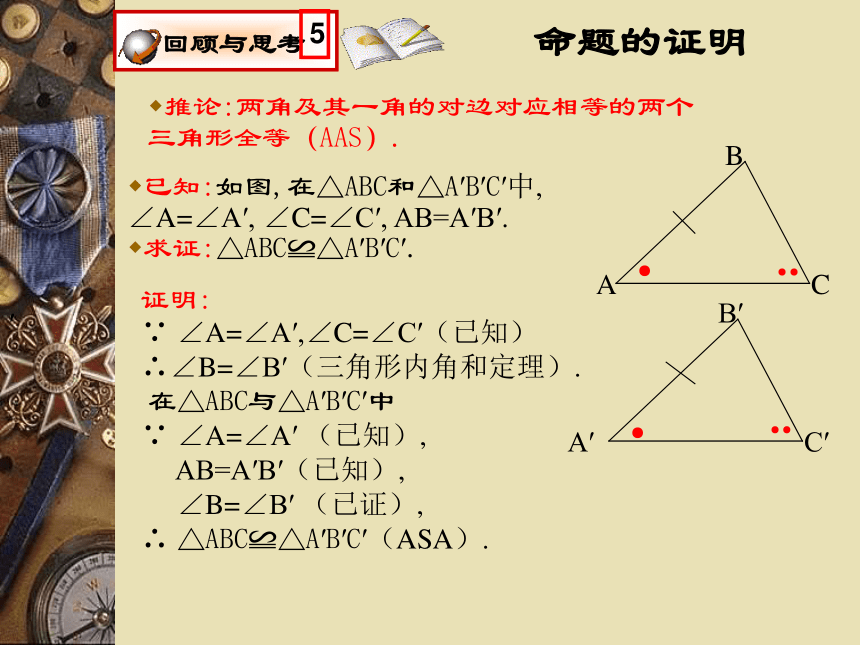
除了刚才所说的三种方法外,还会有其他的方法吗?命题的证明推论:两角及其一角的对边对应相等的两个三角形全等(AAS).证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理).
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).′已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
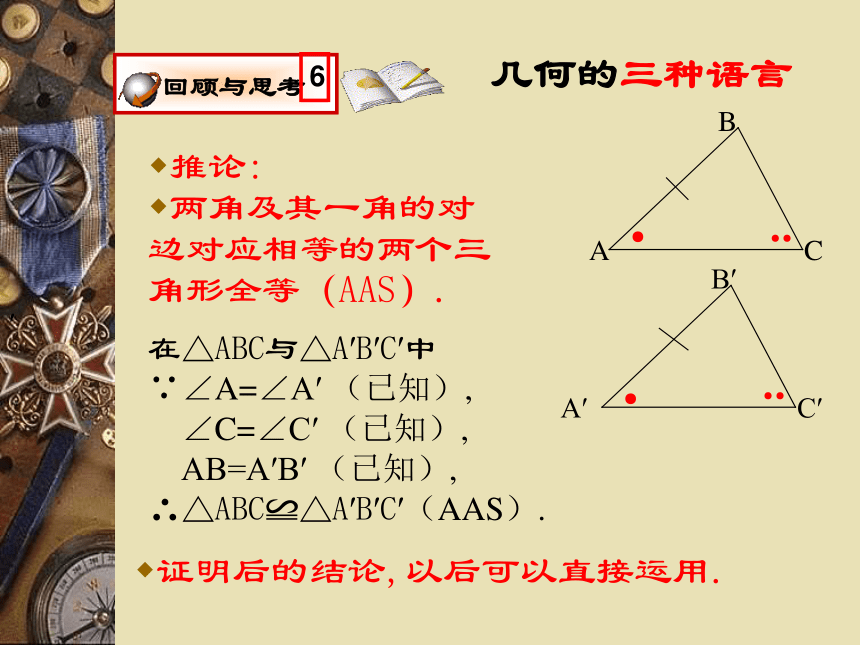
求证:△ABC≌△A′B′C′.几何的三种语言推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).在△ABC与△A′B′C′中
∵∠A=∠A′ (已知),
∠C=∠C′ (已知),
AB=A′B′ (已知),
∴△ABC≌△A′B′C′(AAS).′证明后的结论,以后可以直接运用. 两个三角形共有6个条件:三条边、三个角
我们证明两个三角形全等只需要3个条件。
除了刚才所说的4种方法外,还会有其他的方法吗?SSS、SAS、ASA、AAS快速回答如图:
若__________,∠B=∠B′,BC=B′C′,则 △ABC≌△A′B′C′
若∠B=∠B′,_______,∠C=∠C′,则 △ABC≌△A′B′C′
若∠B=∠B′, ∠C=∠C′,_______,则 △ABC≌△A′B′C′
若AB=A′B′ ,_______,_______,则 △ABC≌△A′B′C′
已知△ABC≌△A′B′C′,则∠A=__________, ∠B=__________, ∠C=__________,AB=__________, BC=__________, CA=__________,几何的三种语言公理:
全等三角形的对应边、对应角相等.在△ABC与△A′B′C′中
∵ △ABC≌△A′B′C′(已知) ∴ AB=A′B′,BC=B′C′,AC=A′C′ (全等三角形的对应边相等);
∠A=∠A′ ,∠B=∠B′,∠C=∠C′(全等三角形的对应角相等).′回味无穷证明两个三角形全等的4种方法,你可记得?要注意一一对应哦。
两个三角形全等的性质可作为证明的一种手段
几何的三种语言融会贯通的水平是否有所提高.要注意书写格式!这个三角形叫做——等腰三角形你知道它有什么特点吗?等腰三角形的性质等腰三角形的性质你能利用已有的公理和定理证明这个结论吗?定理:
等腰三角形的两个底角相等(等边对等角).几何的三种语言定理:
等腰三角形的两个底角相等(等边对等角).如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等角对等边).证明后的结论,以后可以直接运用. 练习:
已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC,求证:AB=AC等腰三角形经过对折,折痕AD有什么特点呢?推论:
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).你能利用已有的公理和定理证明这个结论吗?几何的三种语言推论:
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).如图,在△ABC中,
∵AB=AC, ∠1=∠2(已知).
∴BD=CD,AD⊥BC(三线合一).证明后的结论,以后可以直接运用. 如图,在△ABC中,
∵AB=AC, BD=CD (已知).
∴∠1=∠2,AD⊥BC(三线合一).如图,在△ABC中,
∵AB=AC, AD⊥BC(已知).
∴BD=CD, ∠1=∠2 (三线合一).轮换条件∠1=∠2,
BD=CD,AD⊥BC可得三线合一的三种不同形式的运用.你是如何思考的,请与同伴交流你的做法.′2.前面已经证明了“等边对等角”,反过来,“等角对等边”吗?
即有两个角相等的三角形是等腰三角形吗?已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.分析:要证明AB=AC,只要能构造出AB,AC所在的两个三角形全等就可以了.如:作BC边上的中线;作∠A的平分线或作BC边上的高.等腰三角形的判定几何的三种语言′定理:
有两个角相等的三角形是等腰三角形(等角对等边).在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).这又是一个判定两条线段相等根据之一.1.课堂小测.
2.证明:等边三角形的三个角都相等并且每个角都 等于600.
3. 如图,在△ABD中, C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1).求证:△ABD是等腰三角形;
(2). 求∠BAD的度数.成功者的摇篮5.等腰三角形的一个角等于30°,则它的顶角的度数为___________________________
6.练习24.课本第9页,习题回味无穷理解证明的必要性和规范性.
理解几何命题证明的方法,步骤,格式及注意事项.
你对“执果索因”,“由因导果”理解与运用有何进步.
规范性中的条理清晰,因果相应,言心有据的要求是否内化为一种技能.
几何的三种语言融会贯通的水平是否有所提高.
关注知识,经验,方法的积累和提高,是前进的推进器.
你准备如何提高证明命题的能力呢?学好几何标志是会“证明”证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
等腰三角形的性质、判定这两个三角形的关系是——全等三角形全等的判定方法我们学过那些判定方法?SSS、SAS、ASA几何的三种语言公理:
三边对应相等的两个三角形全等(SSS).在△ABC与△A′B′C′中
∵AB=A′B′(已知)
BC=B′C′ (已知)
AC=A′C′ (已知)∴△ABC≌△A′B′C′(SSS).′几何的三种语言公理:
两边及其夹角对应相等的两个三角形全等(SAS).在△ABC与△A′B′C′中
∵AB=A′B′(已知),
∠A=∠A′ (已知),
BC=B′C′ (已知),
∴△ABC≌△A′B′C′(SAS).′几何的三种语言公理:
两角及其夹边对应相等的两个三角形全等(ASA).在△ABC与△A′B′C′中
∵∠A=∠A′ (已知)
AB=A′B′ (已知) ∠B=∠B′ (已知) ∴△ABC≌△A′B′C′(ASA).′两个三角形共有6个条件:三条边、三个角
我们证明两个三角形全等只需要3个条件。
除了刚才所说的三种方法外,还会有其他的方法吗?命题的证明推论:两角及其一角的对边对应相等的两个三角形全等(AAS).证明:
∵ ∠A=∠A′,∠C=∠C′(已知)∴∠B=∠B′(三角形内角和定理).
在△ABC与△A′B′C′中
∵ ∠A=∠A′ (已知),
AB=A′B′(已知),
∠B=∠B′ (已证),
∴ △ABC≌△A′B′C′(ASA).′已知:如图,在△ABC和△A′B′C′中, ∠A=∠A′, ∠C=∠C′, AB=A′B′.
求证:△ABC≌△A′B′C′.几何的三种语言推论:
两角及其一角的对边对应相等的两个三角形全等(AAS).在△ABC与△A′B′C′中
∵∠A=∠A′ (已知),
∠C=∠C′ (已知),
AB=A′B′ (已知),
∴△ABC≌△A′B′C′(AAS).′证明后的结论,以后可以直接运用. 两个三角形共有6个条件:三条边、三个角
我们证明两个三角形全等只需要3个条件。
除了刚才所说的4种方法外,还会有其他的方法吗?SSS、SAS、ASA、AAS快速回答如图:
若__________,∠B=∠B′,BC=B′C′,则 △ABC≌△A′B′C′
若∠B=∠B′,_______,∠C=∠C′,则 △ABC≌△A′B′C′
若∠B=∠B′, ∠C=∠C′,_______,则 △ABC≌△A′B′C′
若AB=A′B′ ,_______,_______,则 △ABC≌△A′B′C′
已知△ABC≌△A′B′C′,则∠A=__________, ∠B=__________, ∠C=__________,AB=__________, BC=__________, CA=__________,几何的三种语言公理:
全等三角形的对应边、对应角相等.在△ABC与△A′B′C′中
∵ △ABC≌△A′B′C′(已知) ∴ AB=A′B′,BC=B′C′,AC=A′C′ (全等三角形的对应边相等);
∠A=∠A′ ,∠B=∠B′,∠C=∠C′(全等三角形的对应角相等).′回味无穷证明两个三角形全等的4种方法,你可记得?要注意一一对应哦。
两个三角形全等的性质可作为证明的一种手段
几何的三种语言融会贯通的水平是否有所提高.要注意书写格式!这个三角形叫做——等腰三角形你知道它有什么特点吗?等腰三角形的性质等腰三角形的性质你能利用已有的公理和定理证明这个结论吗?定理:
等腰三角形的两个底角相等(等边对等角).几何的三种语言定理:
等腰三角形的两个底角相等(等边对等角).如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等角对等边).证明后的结论,以后可以直接运用. 练习:
已知:如图,点D、E在△ABC的边BC上,AD=AE,BD=EC,求证:AB=AC等腰三角形经过对折,折痕AD有什么特点呢?推论:
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).你能利用已有的公理和定理证明这个结论吗?几何的三种语言推论:
等腰三角形顶角的平分线,底边上的中线,底边上的高互相重合(三线合一).如图,在△ABC中,
∵AB=AC, ∠1=∠2(已知).
∴BD=CD,AD⊥BC(三线合一).证明后的结论,以后可以直接运用. 如图,在△ABC中,
∵AB=AC, BD=CD (已知).
∴∠1=∠2,AD⊥BC(三线合一).如图,在△ABC中,
∵AB=AC, AD⊥BC(已知).
∴BD=CD, ∠1=∠2 (三线合一).轮换条件∠1=∠2,
BD=CD,AD⊥BC可得三线合一的三种不同形式的运用.你是如何思考的,请与同伴交流你的做法.′2.前面已经证明了“等边对等角”,反过来,“等角对等边”吗?
即有两个角相等的三角形是等腰三角形吗?已知:如图,在△ABC中,∠B=∠C.
求证:AB=AC.分析:要证明AB=AC,只要能构造出AB,AC所在的两个三角形全等就可以了.如:作BC边上的中线;作∠A的平分线或作BC边上的高.等腰三角形的判定几何的三种语言′定理:
有两个角相等的三角形是等腰三角形(等角对等边).在△ABC中
∵∠B=∠C(已知),
∴AB=AC(等角对等边).这又是一个判定两条线段相等根据之一.1.课堂小测.
2.证明:等边三角形的三个角都相等并且每个角都 等于600.
3. 如图,在△ABD中, C是BD上的一点,且AC⊥BD,AC=BC=CD.
(1).求证:△ABD是等腰三角形;
(2). 求∠BAD的度数.成功者的摇篮5.等腰三角形的一个角等于30°,则它的顶角的度数为___________________________
6.练习24.课本第9页,习题回味无穷理解证明的必要性和规范性.
理解几何命题证明的方法,步骤,格式及注意事项.
你对“执果索因”,“由因导果”理解与运用有何进步.
规范性中的条理清晰,因果相应,言心有据的要求是否内化为一种技能.
几何的三种语言融会贯通的水平是否有所提高.
关注知识,经验,方法的积累和提高,是前进的推进器.
你准备如何提高证明命题的能力呢?学好几何标志是会“证明”证明命题的一般步骤:(1)理解题意:分清命题的条件(已知),结论(求证);(2)根据题意,画出图形;(3)结合图形,用符号语言写出“已知”和“求证”;(4)分析题意,探索证明思路(由“因”导“果”,执“果”索“因”.);(5)依据思路,运用数学符号和数学语言条理清晰地写出证明过程;(6)检查表达过程是否正确,完善.结束寄语严格性之于数学家,犹如道德之于人.
证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.
