鲁教版(五四制)数学七年级上册 4.2 .2平方根课件(共20张PPT)
文档属性
| 名称 | 鲁教版(五四制)数学七年级上册 4.2 .2平方根课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 272.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
平方根
第二课时
Contents
目录
01
02
03
04
新知探究
基础练习
课堂小结
巩固新知
回顾思考
05
2.我们已经学习过哪些运算?它们中互为
逆运算的是什么?
答:加、减、乘、除、乘方五种运算。加与减互逆;乘与除互逆
1.什么叫算术平方根?
若一个正数的平方等于a 则这个数叫做a的算术平方根,表示为 。
0的平方根是0,即 。
已知折叠着的正方形ABCD面积为1,则边长为_____。将它展开面积变为原来的2倍,那么它的边长为______。若面积变为原来的3倍,则边长为______。若面积变为原来的n倍,则边长为_____。
复习平方与算术平方根之间的关系?
1
问题:乘方有没有逆运算?
(1)9的算术平方根是3,也就是说,3的平方是9。还有其他的数,它的平方也是9吗?
(2)平方等于 的数有几个?平方等于0。64的数呢?
想一想
一般地,如果一个数x的平方等于a,即x2=a,那么这个数叫做a的平方根或二次方根。而把正的平方根叫算术平方根。
例如:(±4)2=16,则+4和-4都是16的平方根;
即16的平方根是±4; +4是16的算术平方根。
平方根的表达式为:
若x2=a,那么x叫做a的平方根,记作: 。
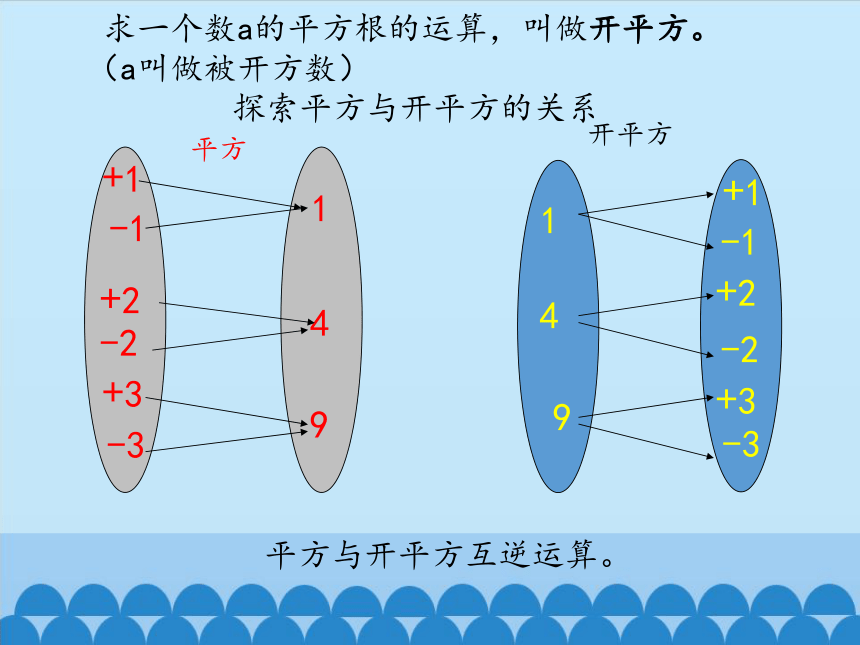
求一个数a的平方根的运算,叫做开平方。
(a叫做被开方数)
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方与开平方互逆运算。
探索平方与开平方的关系
联系:1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种。
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根。
3.0的平方根是0,算术平方根也是0。
区别:
1.个数不同:一个正数有两个平方根,但只有一个算术平方根。
2.表示法不同:平方根表示为 ,而算术平方根表示为 。
1.求下列各数的平方根:
(1)64
(3)0.0004
(5)11
(4)
(2)
1.求下列各数的平方根:
(1)64
(2)
, 的平方根 ,
即 。
解: 64的平方根为 ,
即 。
(3) 0.0004
(5) 11
(4)
, 0.0004的平方根
为 ,即 ;
的平方根
为 ,即 ;
11的平方根是 。
总结:
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数。
注意要弄清 , , 的意义, 不能用来表示a的平方根,如:64的平方根不要写成 。
议一议
一个正数有几个平方根?它们是什么关系?
0的平方根有几个?
负数有平方根吗?
一个正数有两个平方根,它们是互为相反数。
一个,0的平方根是0。
负数没有平方根。
1. 的平方根 , 的算术平方根
是_____, 的平方根是_____;
2 . =___, _____, ____,
_____;
3. _____, 当a ≥0时, ___。
±5
3
9
±8
0.2
a
5
二、下列说法不正确的是( )
A.0的平方根是0。 B. 的平方根是2。
C.非负数的平方根是互为相反数。
D.一个正整数的算术平方根一定大于这个数的相反数。
一、下列说法正确的是_________
① -3是的 平方根 ②25的平方根是5
③ -36的平方根是-6 ④平方根等于0的数是0
⑤6的算术平方根是8
① ④
B
三、已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是( )
A. a+1 B.
C. a2+1 D.
D
四、x为何值时, 有意义?
答:因为 ,所以 。
五、求 x 的值,
解:
,
,
,
或
,
或
。
知识总结
若 ,则x叫a的平方根, 。
正数有2个平方根,0的平方根是0。
负数没有平方根。
方法总结:
求一个数的平方根就是寻找哪个数平方等于这个数平方与开方的互逆关系。
作业布置
习题4.4 知识技能
谢 谢
平方根
第二课时
Contents
目录
01
02
03
04
新知探究
基础练习
课堂小结
巩固新知
回顾思考
05
2.我们已经学习过哪些运算?它们中互为
逆运算的是什么?
答:加、减、乘、除、乘方五种运算。加与减互逆;乘与除互逆
1.什么叫算术平方根?
若一个正数的平方等于a 则这个数叫做a的算术平方根,表示为 。
0的平方根是0,即 。
已知折叠着的正方形ABCD面积为1,则边长为_____。将它展开面积变为原来的2倍,那么它的边长为______。若面积变为原来的3倍,则边长为______。若面积变为原来的n倍,则边长为_____。
复习平方与算术平方根之间的关系?
1
问题:乘方有没有逆运算?
(1)9的算术平方根是3,也就是说,3的平方是9。还有其他的数,它的平方也是9吗?
(2)平方等于 的数有几个?平方等于0。64的数呢?
想一想
一般地,如果一个数x的平方等于a,即x2=a,那么这个数叫做a的平方根或二次方根。而把正的平方根叫算术平方根。
例如:(±4)2=16,则+4和-4都是16的平方根;
即16的平方根是±4; +4是16的算术平方根。
平方根的表达式为:
若x2=a,那么x叫做a的平方根,记作: 。
求一个数a的平方根的运算,叫做开平方。
(a叫做被开方数)
1
4
9
+1
-1
+2
-2
+3
-3
1
4
9
+1
-1
+2
-2
+3
-3
开平方
平方
平方与开平方互逆运算。
探索平方与开平方的关系
联系:1.包含关系:平方根包含算术平方根,算术平方根是平方根的一种。
平方根与算术平方根的联系与区别:
2.只有非负数才有平方根和算术平方根。
3.0的平方根是0,算术平方根也是0。
区别:
1.个数不同:一个正数有两个平方根,但只有一个算术平方根。
2.表示法不同:平方根表示为 ,而算术平方根表示为 。
1.求下列各数的平方根:
(1)64
(3)0.0004
(5)11
(4)
(2)
1.求下列各数的平方根:
(1)64
(2)
, 的平方根 ,
即 。
解: 64的平方根为 ,
即 。
(3) 0.0004
(5) 11
(4)
, 0.0004的平方根
为 ,即 ;
的平方根
为 ,即 ;
11的平方根是 。
总结:
运用平方运算求一个非负数的平方根是常用的方法,如被开方数是小数,要注意小数点的位置,也可先将小数化为分数,再求它的平方根,如被开方数是带分数,先要把它化为假分数。
注意要弄清 , , 的意义, 不能用来表示a的平方根,如:64的平方根不要写成 。
议一议
一个正数有几个平方根?它们是什么关系?
0的平方根有几个?
负数有平方根吗?
一个正数有两个平方根,它们是互为相反数。
一个,0的平方根是0。
负数没有平方根。
1. 的平方根 , 的算术平方根
是_____, 的平方根是_____;
2 . =___, _____, ____,
_____;
3. _____, 当a ≥0时, ___。
±5
3
9
±8
0.2
a
5
二、下列说法不正确的是( )
A.0的平方根是0。 B. 的平方根是2。
C.非负数的平方根是互为相反数。
D.一个正整数的算术平方根一定大于这个数的相反数。
一、下列说法正确的是_________
① -3是的 平方根 ②25的平方根是5
③ -36的平方根是-6 ④平方根等于0的数是0
⑤6的算术平方根是8
① ④
B
三、已知一个自然数的算术平方根是a,则该自然数的下一个自然数的算术平方根是( )
A. a+1 B.
C. a2+1 D.
D
四、x为何值时, 有意义?
答:因为 ,所以 。
五、求 x 的值,
解:
,
,
,
或
,
或
。
知识总结
若 ,则x叫a的平方根, 。
正数有2个平方根,0的平方根是0。
负数没有平方根。
方法总结:
求一个数的平方根就是寻找哪个数平方等于这个数平方与开方的互逆关系。
作业布置
习题4.4 知识技能
谢 谢
