人教A版必修二 1.1.1 空间几何体的结构特征(第二课时)
文档属性
| 名称 | 人教A版必修二 1.1.1 空间几何体的结构特征(第二课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-23 00:00:00 | ||
图片预览


文档简介
课件28张PPT。1.1.1 棱柱、棱锥和棱台湖南省耒阳市振兴学校
高中数学老师欧阳文丰
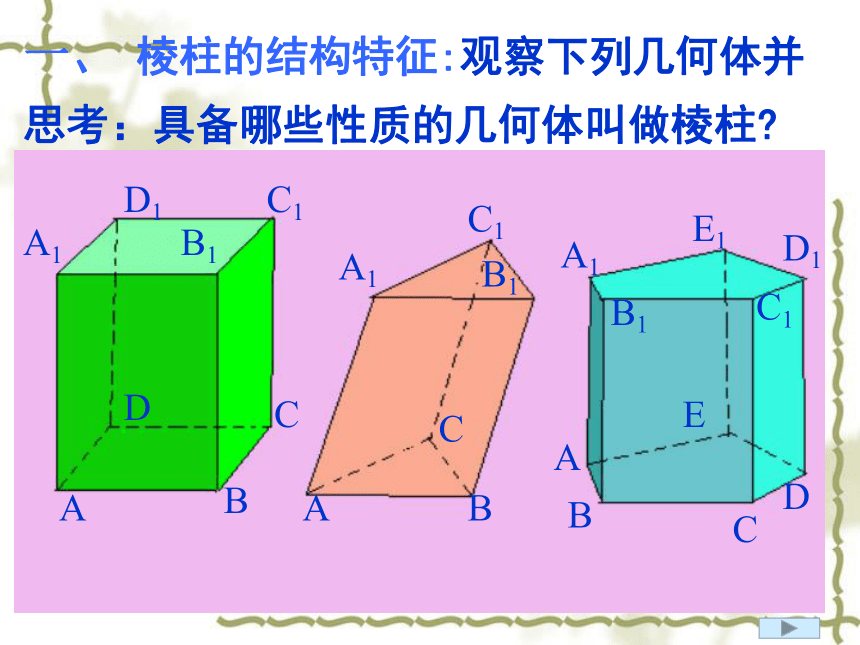
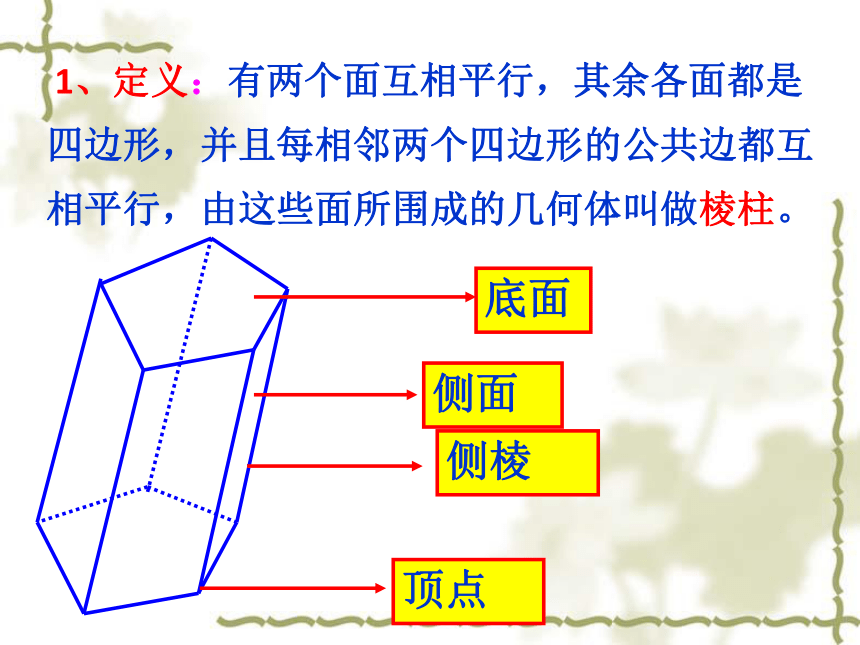
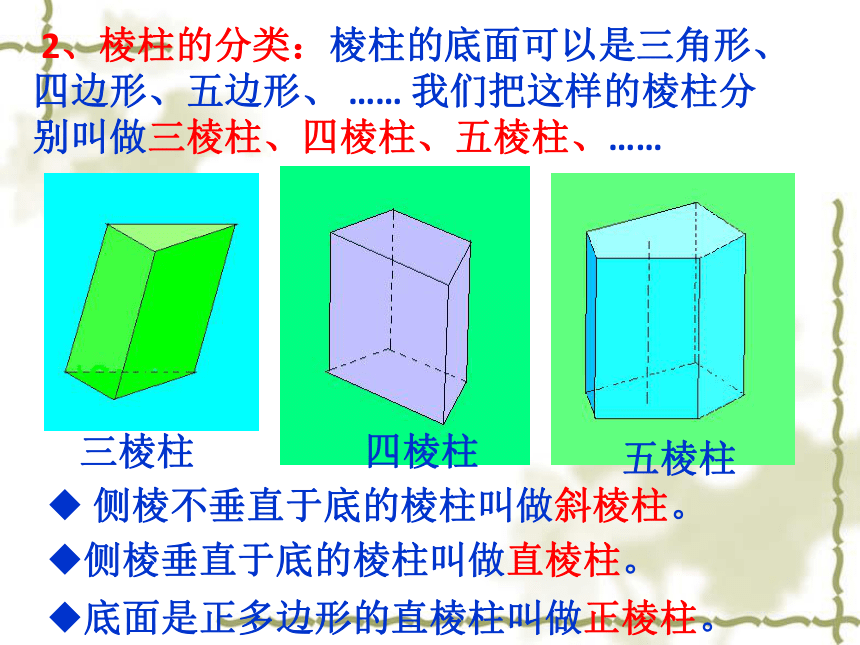
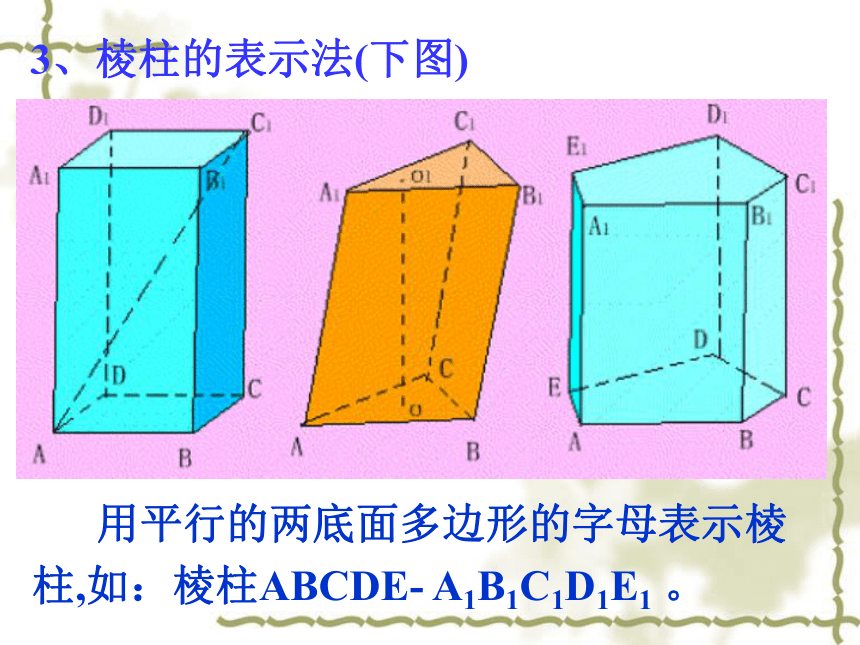
制作于2012年10月23日一、 棱柱的结构特征:观察下列几何体并思考:具备哪些性质的几何体叫做棱柱?ABCDA1A1B1B1C1C1D1ABC 1、定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。三棱柱四棱柱五棱柱 侧棱不垂直于底的棱柱叫做斜棱柱。侧棱垂直于底的棱柱叫做直棱柱。底面是正多边形的直棱柱叫做正棱柱。 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。观察下列几何体,回答①两个底面多边形间的关系?②上下底面对应边间的关系?
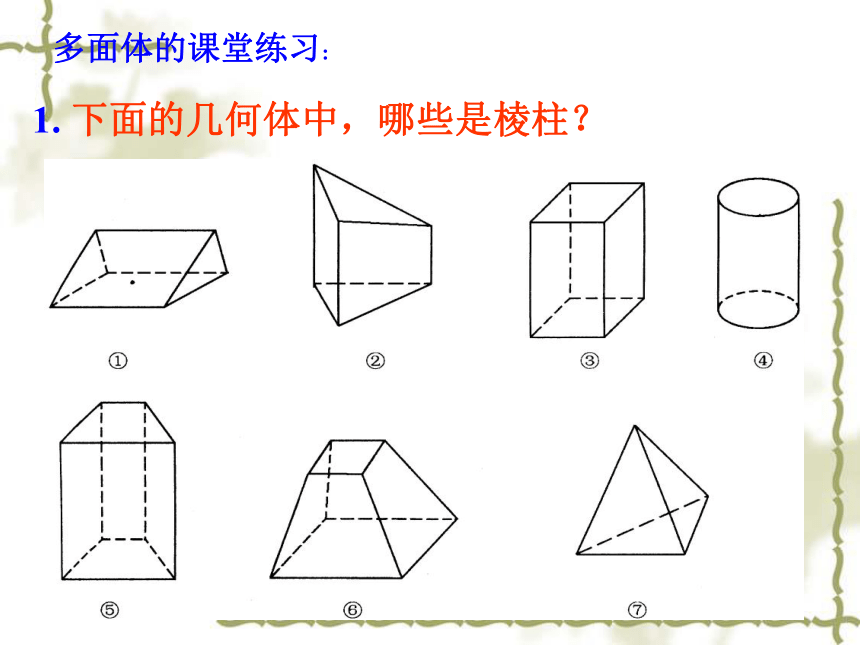
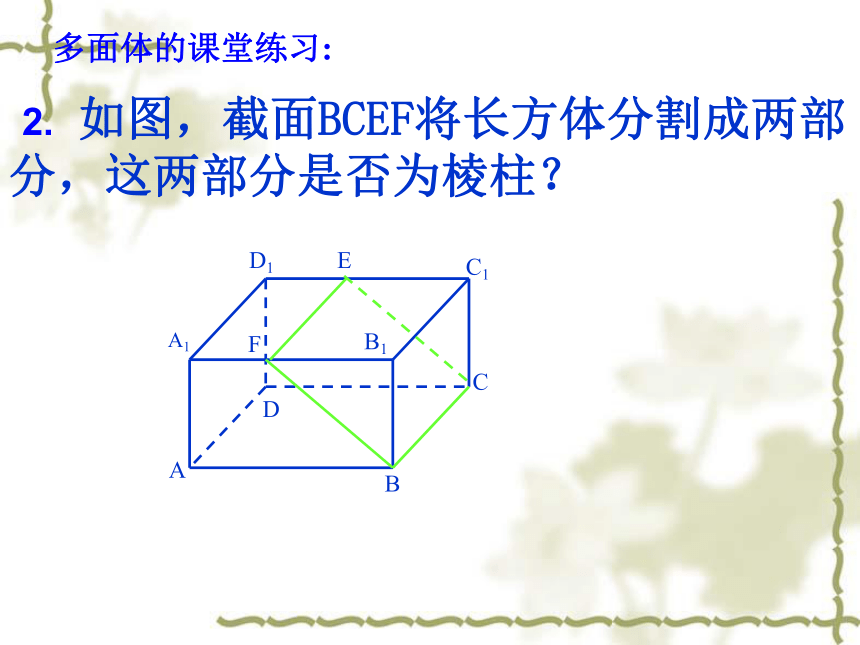
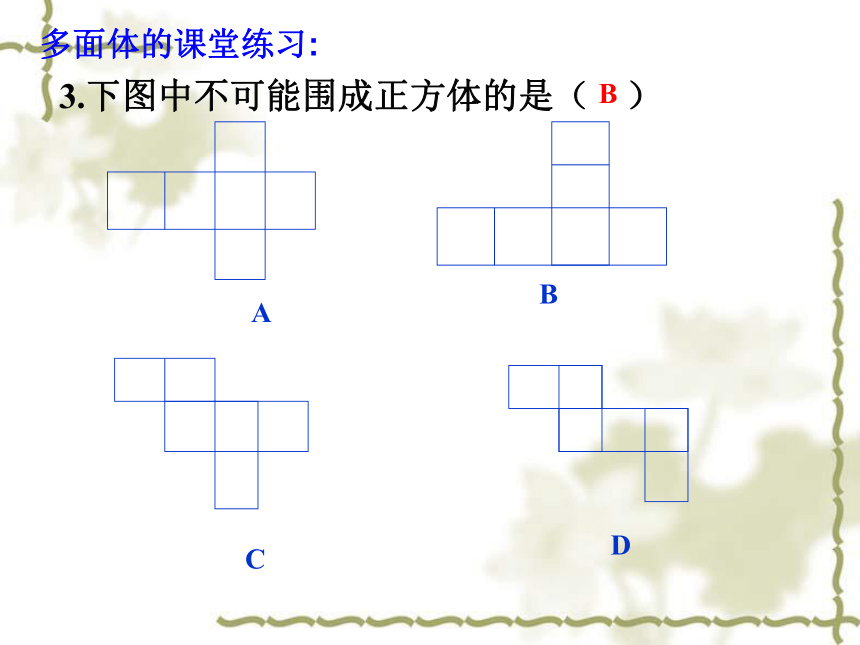
④侧棱之间的关系?③侧面是什么平面图形?全等平行平行平行四边形棱柱的性质:两个底面是全等的多边形,对应边互相平行,侧面都是平行四边形, 侧棱平行.4.棱柱的性质多面体的课堂练习:1. 下面的几何体中,哪些是棱柱? 2. 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱? 多面体的课堂练习:3.下图中不可能围成正方体的是( )B多面体的课堂练习:4.在棱柱中………………..( )A . 只有两个面平行B . 所有的棱都相等C . 所有的面都是平行四边形D . 两底面平行,并且各侧棱也平行D5. 已知长方体的长、宽、高之比为4∶3∶12,对角线长为26cm, 则长、宽、高分别为多少?6、 长方体AC1中,AB=3,BC=2,BB1=1,由A到C1在长方体表面上的最短距离是多少?7、长方体按如图截去一角后所得的两部分还是棱柱吗?ABCDA’B’C’D’EFGHF’E’H’G’ 答:都是棱柱.二、棱锥的结构特征观察下列几何体,有什么相同点?1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。SABCDE下列命题是否正确?
有一个面是多边形,其余各面都是三角形的立体图形一定是棱锥.思考明矾晶体2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。4、如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.观察下列棱锥,归纳它们的底面和侧面各有什么特征?棱锥的性质:①底面是多边形(如三角形、四边形、五边形等)在同一个棱锥中的各个侧面三角形有什么共同特征?②侧面是三角形有一个公共顶点的5、棱锥的性质6、正棱锥的性质 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥. 各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。多面体的课堂练习: 8.一个三棱柱可以分割成几个三棱锥?三、棱台的结构特征BCADSB1A1C1D11、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。4、用正棱锥截得的棱台叫作正棱台。斜高用正棱锥截得的棱台叫作正棱台。正棱台正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。正棱锥正四棱台判断:下列几何体是不是棱台,为什么?(1)(2)辨析1.判断:有一个面是多边形,其余各面都是三角形的几何
体是棱锥. ( )2.如图,四棱柱的六个面都是平行四边形,这个四棱柱可以
由哪个平面图形按怎样的方向平移得到?3.将下列几何体按结构特征分类填空
①集装箱 ②魔方 ③金字塔 ④三棱镜
⑤一个四棱锥形的建筑物被台风刮走了一个顶,
剩下的上底面与地面平行(1)棱柱结构特征的有:
(2)棱锥结构特征的有:
(3)棱台结构特征的有:
①②④③⑤课堂练习×棱柱、棱锥、棱台的结构特征比较两底面是全等的多边形平行四边形平行且相等与两底面是全等的多边形平行四边形多边形三角形相交于顶点与底面是相似的多边形三角形两底面是相似的多边形梯形延长线交于一点与两底面是相似的多边形梯形思考问题:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点(1)棱柱、棱锥、棱台的定义和性质
(2)运动变化、类比联想的观点
(3)将空间问题转化成平面问题的转化思想回顾小结
高中数学老师欧阳文丰
制作于2012年10月23日一、 棱柱的结构特征:观察下列几何体并思考:具备哪些性质的几何体叫做棱柱?ABCDA1A1B1B1C1C1D1ABC 1、定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。三棱柱四棱柱五棱柱 侧棱不垂直于底的棱柱叫做斜棱柱。侧棱垂直于底的棱柱叫做直棱柱。底面是正多边形的直棱柱叫做正棱柱。 2、棱柱的分类:棱柱的底面可以是三角形、四边形、五边形、 …… 我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱、…… 3、棱柱的表示法(下图) 用平行的两底面多边形的字母表示棱柱,如:棱柱ABCDE- A1B1C1D1E1 。观察下列几何体,回答①两个底面多边形间的关系?②上下底面对应边间的关系?
④侧棱之间的关系?③侧面是什么平面图形?全等平行平行平行四边形棱柱的性质:两个底面是全等的多边形,对应边互相平行,侧面都是平行四边形, 侧棱平行.4.棱柱的性质多面体的课堂练习:1. 下面的几何体中,哪些是棱柱? 2. 如图,截面BCEF将长方体分割成两部分,这两部分是否为棱柱? 多面体的课堂练习:3.下图中不可能围成正方体的是( )B多面体的课堂练习:4.在棱柱中………………..( )A . 只有两个面平行B . 所有的棱都相等C . 所有的面都是平行四边形D . 两底面平行,并且各侧棱也平行D5. 已知长方体的长、宽、高之比为4∶3∶12,对角线长为26cm, 则长、宽、高分别为多少?6、 长方体AC1中,AB=3,BC=2,BB1=1,由A到C1在长方体表面上的最短距离是多少?7、长方体按如图截去一角后所得的两部分还是棱柱吗?ABCDA’B’C’D’EFGHF’E’H’G’ 答:都是棱柱.二、棱锥的结构特征观察下列几何体,有什么相同点?1、棱锥的概念 有一个面是多边形,其余各面是有一个公共顶点的三角形, 由这些面所围成的几何体叫做棱锥。SABCDE下列命题是否正确?
有一个面是多边形,其余各面都是三角形的立体图形一定是棱锥.思考明矾晶体2、棱锥的分类:
按底面多边形的边数,可以分为三棱锥、四棱锥、五棱锥、……3、棱锥的表示方法:用表示顶点和底面的字母表示,如四棱锥S-ABCD。4、如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥.观察下列棱锥,归纳它们的底面和侧面各有什么特征?棱锥的性质:①底面是多边形(如三角形、四边形、五边形等)在同一个棱锥中的各个侧面三角形有什么共同特征?②侧面是三角形有一个公共顶点的5、棱锥的性质6、正棱锥的性质 如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥是正棱锥. 各侧棱相等,各侧面 是全等的等腰三角形,各等腰 三角形底边上的高相等(它叫做正棱锥的斜高)。多面体的课堂练习: 8.一个三棱柱可以分割成几个三棱锥?三、棱台的结构特征BCADSB1A1C1D11、棱台的概念:用一个平行于棱锥底面的平面去截棱锥,底面和截面之间的部分叫做棱台。2、由三棱锥、四棱锥、五棱锥…截得的棱台,分别叫做三棱台,四棱台,五棱台…3、棱台的表示法:棱台用表示上、下底面各顶点的字母来表示,如右图,棱台ABCD-A1B1C1D1 。4、用正棱锥截得的棱台叫作正棱台。斜高用正棱锥截得的棱台叫作正棱台。正棱台正棱台的侧面是全等的等腰梯形,
它的高叫作正棱台的斜高。正棱锥正四棱台判断:下列几何体是不是棱台,为什么?(1)(2)辨析1.判断:有一个面是多边形,其余各面都是三角形的几何
体是棱锥. ( )2.如图,四棱柱的六个面都是平行四边形,这个四棱柱可以
由哪个平面图形按怎样的方向平移得到?3.将下列几何体按结构特征分类填空
①集装箱 ②魔方 ③金字塔 ④三棱镜
⑤一个四棱锥形的建筑物被台风刮走了一个顶,
剩下的上底面与地面平行(1)棱柱结构特征的有:
(2)棱锥结构特征的有:
(3)棱台结构特征的有:
①②④③⑤课堂练习×棱柱、棱锥、棱台的结构特征比较两底面是全等的多边形平行四边形平行且相等与两底面是全等的多边形平行四边形多边形三角形相交于顶点与底面是相似的多边形三角形两底面是相似的多边形梯形延长线交于一点与两底面是相似的多边形梯形思考问题:既然棱柱、棱锥、棱台都是多面体,那么它们之间有怎样的关系?当底面发生变化时,它们能否相互转化?棱台的上底面扩大
上下底面全等棱台的上底面缩小
为一个点(1)棱柱、棱锥、棱台的定义和性质
(2)运动变化、类比联想的观点
(3)将空间问题转化成平面问题的转化思想回顾小结
