人教A版必修二 1.1.1 空间几何体的结构特征(第三课时)
文档属性
| 名称 | 人教A版必修二 1.1.1 空间几何体的结构特征(第三课时) |  | |
| 格式 | zip | ||
| 文件大小 | 309.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-10-23 18:20:32 | ||
图片预览



文档简介
课件25张PPT。圆柱、圆锥、
圆台的结构特征湖南省耒阳市振兴学校
高中数学老师欧阳文丰
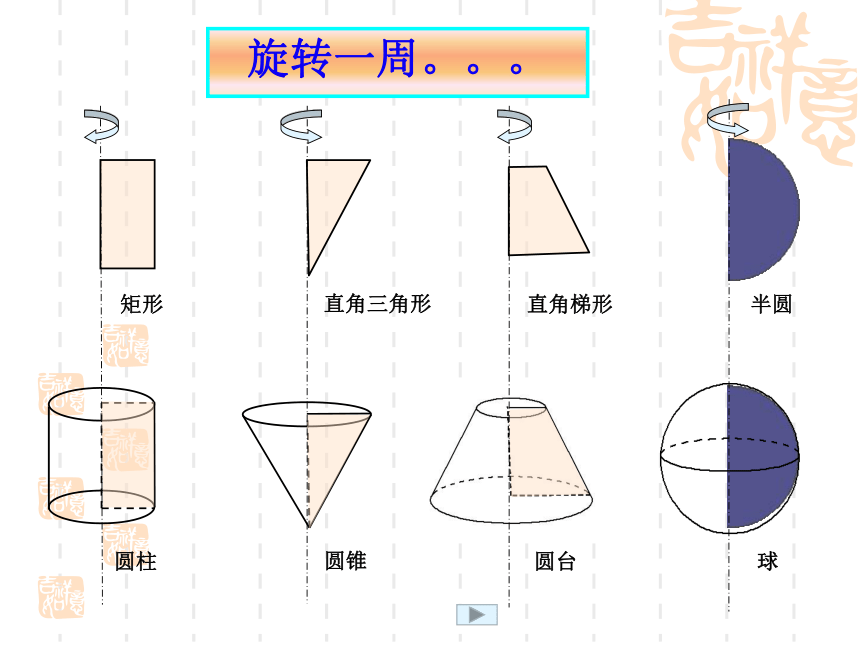
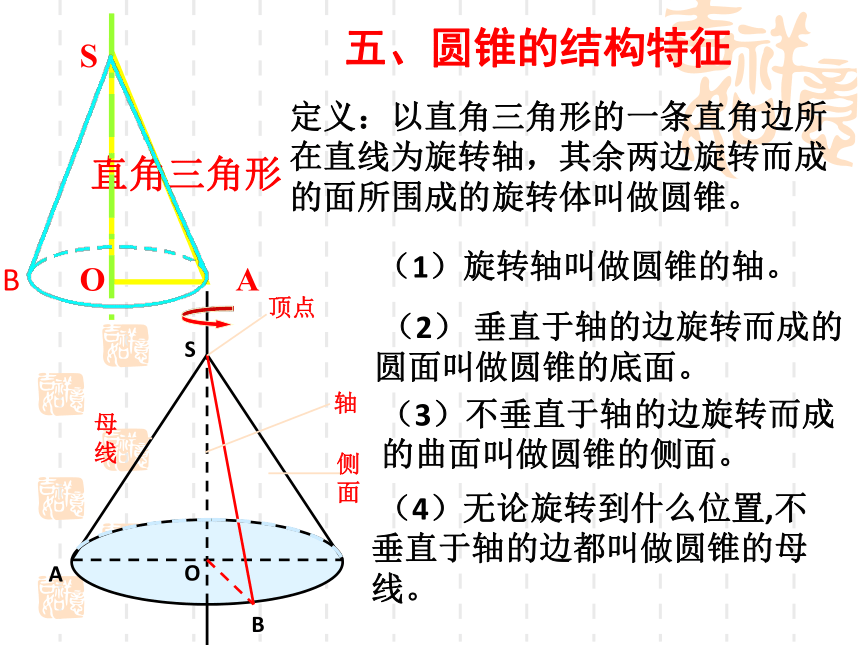
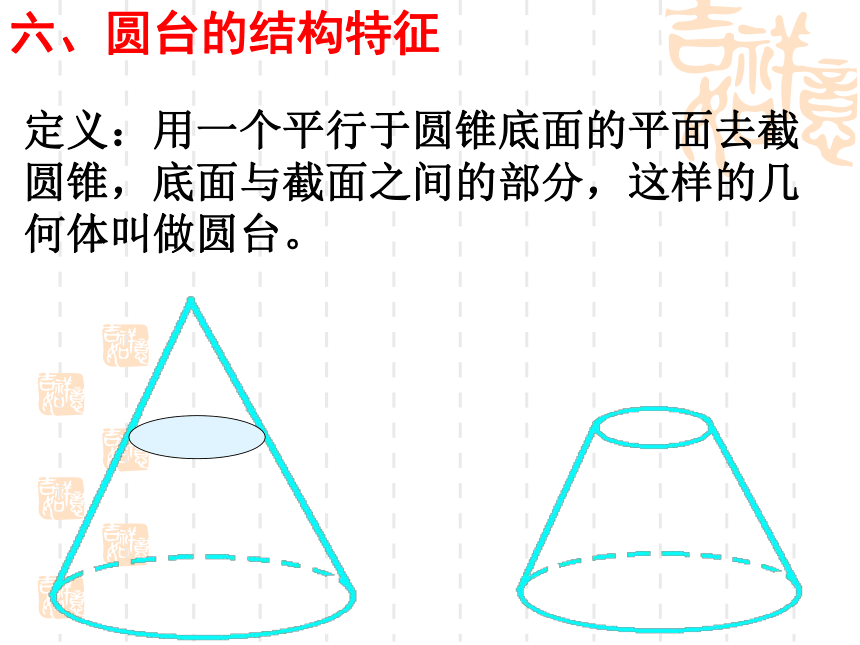
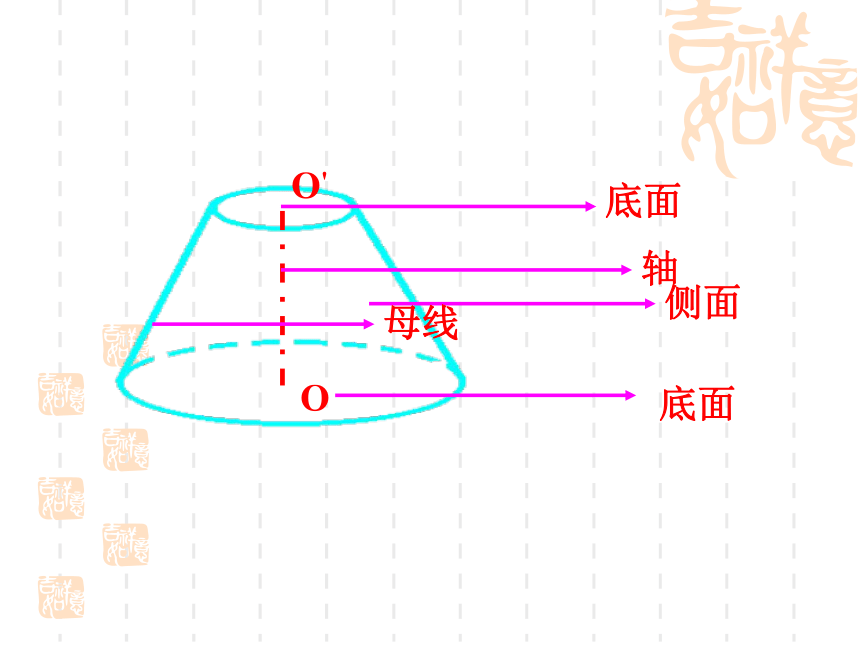
制作于2012年10月23日旋转一周。。。矩形直角三角形半圆直角梯形圆柱圆锥球圆台四、圆柱的结构特征矩 形O1O 定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱。 (4)无论旋转到什么位置,不垂直于轴的边都叫做圆柱的母线。 (3)平行于轴的边旋转而成的曲面 叫做圆柱的侧面。 (2) 垂直于轴的边旋转而成的圆面叫做圆柱的底面。(1)旋转轴叫做圆柱的轴。A’B’AA’OBO’五、圆锥的结构特征直角三角形SAO (4)无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线。(3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。 (2) 垂直于轴的边旋转而成的圆面叫做圆锥的底面。(1)旋转轴叫做圆锥的轴。定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转而成的面所围成的旋转体叫做圆锥。SABOB六、圆台的结构特征定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台。 1.平行于圆柱,圆锥,圆台的
底面的截面是什么图形?
2.过圆柱,圆锥,圆台的旋转
轴的截面是什么图形?性质1:平行于底面的截面都是圆。性质2:过轴的截面(轴截面)分别是全等的矩
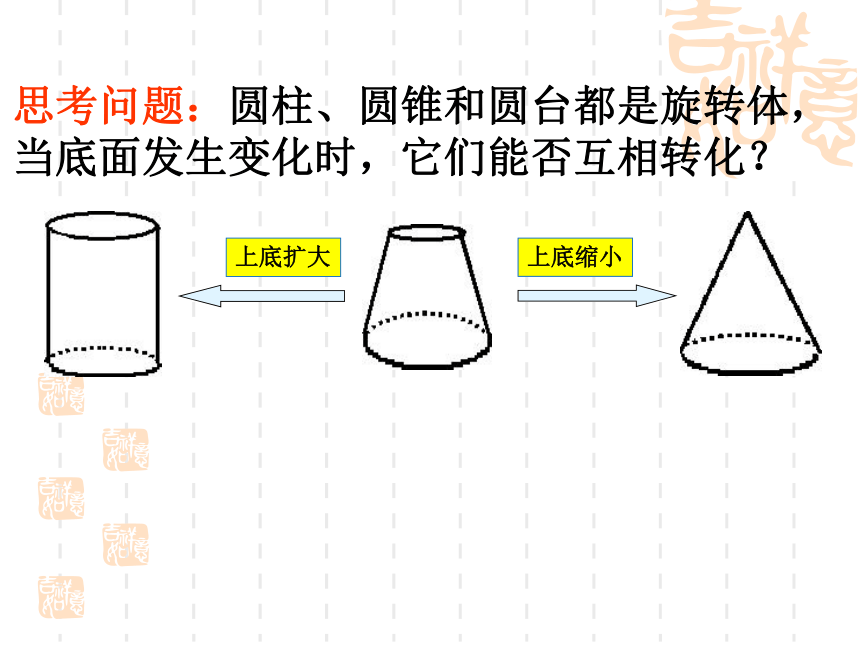
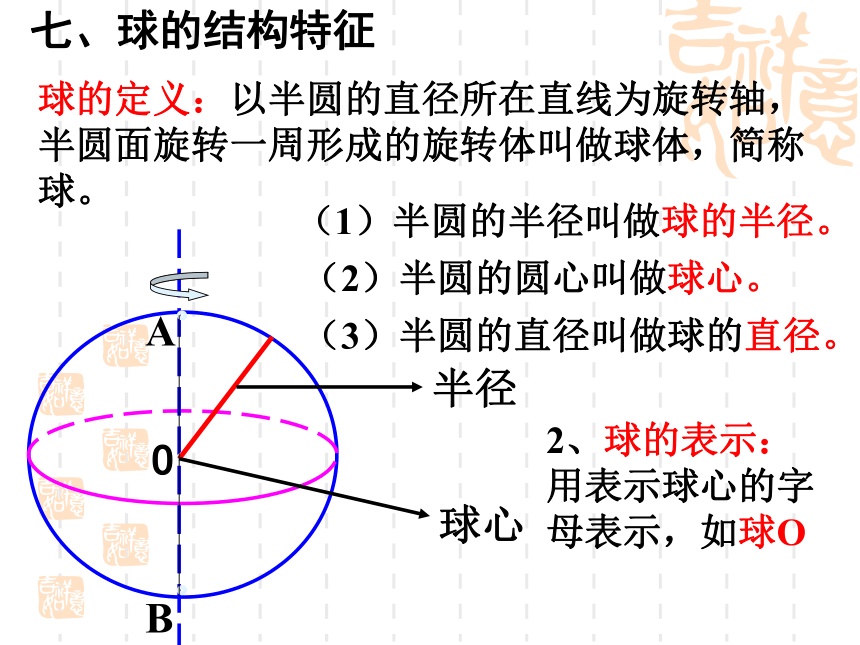
形,等腰三角形,等腰梯形。思考问题:圆柱、圆锥和圆台都是旋转体,当底面发生变化时,它们能否互相转化?七、球的结构特征O球心半径AB球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心。(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球球面:半圆弧旋转所成的曲面.轴其中半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径。用一个平面去截球体得到的截面是什么图形? 性质3:用一个平面去截球体得到的截面是一个圆。想一想:用一个平面去截一个球,截面是什么?O 用一个截面去截一个球,截面是圆面。球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的截面截得的圆叫球的小圆。思考问题:设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系如何?球、圆柱、圆锥、圆台过轴的截面(轴截面)分别是什么图形? 例1 将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?[例题讲解]例2 把一个圆锥截成 圆台,已知圆台的上、
下底面半径的比是1:4,母线长为10cm,
求圆锥的母线长。设圆锥的母线长为 y ,则有解: (y-10):y= 4(y-10)=y8cm课堂练习:1、下列命题是正确的是( )A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。A2、过球面上的两点作球的大圆,可以作( )个。1或无数多3. 说出下列图形绕虚线旋转一周,可以形成怎样的几何体? 1、一个等腰梯形绕着两底边中点的连线所在的直线旋转180度形成的封闭曲面所围成的几何体是______圆台 3、一个等腰三角形绕着底边上的高所在的直线旋转180度形成的封闭曲面所围成的几何体是__圆锥 2.一个矩形绕着一边的中垂线旋转
180度形成的封闭曲面所围成的几何体
是____圆柱补充练习4.下列表达不正确的是 ( )
A 以矩形的一边所在直线为旋转轴,其余 三边旋转形成的曲面所围成的几何体叫圆柱
B 以直角三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
C 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
D 以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成的曲面围成的几何体叫圆锥B5、下列表达不正确的是( )
A 用平行于圆锥底面的平面截圆锥,
截面和底面之间的部分是圆台
B 以直角梯形的一腰为旋转轴,
另一腰为母线的旋转面是圆台的侧面
C 圆柱、圆锥、圆台的底面都是圆.
D 圆台的母线延长后与轴交于同一点B6、有下列命题:
(1)在圆柱的上下底面圆周上各取一点,
则这两点的连线是圆柱的母线;
(2)圆锥顶点与底面圆周上任意一点的
连线是圆锥的母线;
(3)在圆台上下底面的圆周上各取一点,
则这两点的连线是圆台的母线;
(4)圆柱的任意两条母线所在的直线
是互相平行的。
其中正确的是( )
A(1)(2) B(2)(3)
C(1)(3) D (2)(4)D 课后练习已知圆锥的轴截面等腰三角形的腰长为 5cm,面积为12cm,求圆锥的底面半径.
2.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.
3、把一个圆锥截成圆台,截去的圆锥与圆台的母线长比为2:1,圆台的上底面半径为6cm,问下底面半径比上底面半径多多少?
几何体的分类柱体锥体台体球多面体旋转体
圆台的结构特征湖南省耒阳市振兴学校
高中数学老师欧阳文丰
制作于2012年10月23日旋转一周。。。矩形直角三角形半圆直角梯形圆柱圆锥球圆台四、圆柱的结构特征矩 形O1O 定义:以矩形的一边所在直线为旋转轴,其余三边旋转形成的曲面所围成的旋转体叫做圆柱。 (4)无论旋转到什么位置,不垂直于轴的边都叫做圆柱的母线。 (3)平行于轴的边旋转而成的曲面 叫做圆柱的侧面。 (2) 垂直于轴的边旋转而成的圆面叫做圆柱的底面。(1)旋转轴叫做圆柱的轴。A’B’AA’OBO’五、圆锥的结构特征直角三角形SAO (4)无论旋转到什么位置,不垂直于轴的边都叫做圆锥的母线。(3)不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。 (2) 垂直于轴的边旋转而成的圆面叫做圆锥的底面。(1)旋转轴叫做圆锥的轴。定义:以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转而成的面所围成的旋转体叫做圆锥。SABOB六、圆台的结构特征定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分,这样的几何体叫做圆台。 1.平行于圆柱,圆锥,圆台的
底面的截面是什么图形?
2.过圆柱,圆锥,圆台的旋转
轴的截面是什么图形?性质1:平行于底面的截面都是圆。性质2:过轴的截面(轴截面)分别是全等的矩
形,等腰三角形,等腰梯形。思考问题:圆柱、圆锥和圆台都是旋转体,当底面发生变化时,它们能否互相转化?七、球的结构特征O球心半径AB球的定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的旋转体叫做球体,简称球。(1)半圆的半径叫做球的半径。(2)半圆的圆心叫做球心。(3)半圆的直径叫做球的直径。2、球的表示:用表示球心的字母表示,如球O球球面:半圆弧旋转所成的曲面.轴其中半圆的圆心叫做球的球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径。用一个平面去截球体得到的截面是什么图形? 性质3:用一个平面去截球体得到的截面是一个圆。想一想:用一个平面去截一个球,截面是什么?O 用一个截面去截一个球,截面是圆面。球面被经过球心的平面截得的圆叫做大圆。
球面被不过球心的截面截得的圆叫球的小圆。思考问题:设球的半径为R,截面圆半径为r,球心与截面圆圆心的距离为d,则R、r、d三者之间的关系如何?球、圆柱、圆锥、圆台过轴的截面(轴截面)分别是什么图形? 例1 将下列平面图形绕直线AB旋转一周,所得的几何体分别是什么?[例题讲解]例2 把一个圆锥截成 圆台,已知圆台的上、
下底面半径的比是1:4,母线长为10cm,
求圆锥的母线长。设圆锥的母线长为 y ,则有解: (y-10):y= 4(y-10)=y8cm课堂练习:1、下列命题是正确的是( )A 以直角三角形的一直角边所在的直线为轴旋转所得的几何体为圆锥;
B 以直角梯形的一腰所在的直线为轴旋转所得的旋转体为圆柱;
C 圆柱、圆锥、棱锥的底面都是圆;
D 有一个面为多边形,其他各面都是三角形的几何体是棱锥。A2、过球面上的两点作球的大圆,可以作( )个。1或无数多3. 说出下列图形绕虚线旋转一周,可以形成怎样的几何体? 1、一个等腰梯形绕着两底边中点的连线所在的直线旋转180度形成的封闭曲面所围成的几何体是______圆台 3、一个等腰三角形绕着底边上的高所在的直线旋转180度形成的封闭曲面所围成的几何体是__圆锥 2.一个矩形绕着一边的中垂线旋转
180度形成的封闭曲面所围成的几何体
是____圆柱补充练习4.下列表达不正确的是 ( )
A 以矩形的一边所在直线为旋转轴,其余 三边旋转形成的曲面所围成的几何体叫圆柱
B 以直角三角形的一条边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
C 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面围成的几何体叫圆锥
D 以等腰三角形的底边上的高所在直线为旋转轴,其余各边旋转形成的曲面围成的几何体叫圆锥B5、下列表达不正确的是( )
A 用平行于圆锥底面的平面截圆锥,
截面和底面之间的部分是圆台
B 以直角梯形的一腰为旋转轴,
另一腰为母线的旋转面是圆台的侧面
C 圆柱、圆锥、圆台的底面都是圆.
D 圆台的母线延长后与轴交于同一点B6、有下列命题:
(1)在圆柱的上下底面圆周上各取一点,
则这两点的连线是圆柱的母线;
(2)圆锥顶点与底面圆周上任意一点的
连线是圆锥的母线;
(3)在圆台上下底面的圆周上各取一点,
则这两点的连线是圆台的母线;
(4)圆柱的任意两条母线所在的直线
是互相平行的。
其中正确的是( )
A(1)(2) B(2)(3)
C(1)(3) D (2)(4)D 课后练习已知圆锥的轴截面等腰三角形的腰长为 5cm,面积为12cm,求圆锥的底面半径.
2.已知圆柱的底面半径为3cm,,轴截面面积为24cm,求圆柱的母线长.
3、把一个圆锥截成圆台,截去的圆锥与圆台的母线长比为2:1,圆台的上底面半径为6cm,问下底面半径比上底面半径多多少?
几何体的分类柱体锥体台体球多面体旋转体
