阶段综合练(范围6.1线段、射线、直线~6.2角)2021-2022学年苏科版七年级数学上册(word版含解析)
文档属性
| 名称 | 阶段综合练(范围6.1线段、射线、直线~6.2角)2021-2022学年苏科版七年级数学上册(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 08:32:34 | ||
图片预览



文档简介
阶段综合练(范围6.1线段、射线、直线~6.2角)
2021-2022学年苏科版七年级数学上册
一、选择题
1、在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( ).
A.①③ B.②③ C.③④ D.②④
2、下列四个图形中,能用、、三种方法表示同一角的图形是( )
A.B.C. D.
3、将化成度分秒表示,结果是( )
A. B. C. D.
4、下列说法中正确的是( )
A.8时45分,时针与分针的夹角是30° B.6时30分,时针与分针重合
C.3时30分,时针与分针的夹角是90° D.3时整,时针与分针的夹角是90°
5、对于题目:“如图1,已知A,B为两个海岛,点B在点A的正东方向,若灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,请画出灯塔C的位置.”甲、乙两人分别作出了如下解答:
甲:先以A为参照点,作南偏东25°,再以B为参照点,作南偏西65°,画出图形如图2.
乙:先以A为参照点,作东偏北25°,再以B为参照点,作西偏北55°,画出图形如图3.
下列判断正确的是( )
A.甲的说法和画图都正确 B.乙的说法正确,画图错误
C.乙的说法和画图都正确 D.甲乙的说法都错误
6、如图,已知D是线段中点,延长线段至C使,则下列结论中①:②;③;④;⑤;⑥,正确的有( )
A.①③④⑥ B.①②⑤⑥ C.①②③④ D.②③⑤⑥
7、如图,是线段上两点,若且是的中点,则的长等于( )
A. B. C. D.
8、已知线段AB=6,C是直线AB上一点,BC=3,则线段AC长为( )
A.6 B.3 C.6或9 D.3或9
9、已知,都是钝角,甲、乙、丙、丁四名同学计算的结果依次是,,,,
其中 有一名同学计算错误,这名同学是( )
A.甲 B.乙 C.丙 D.丁
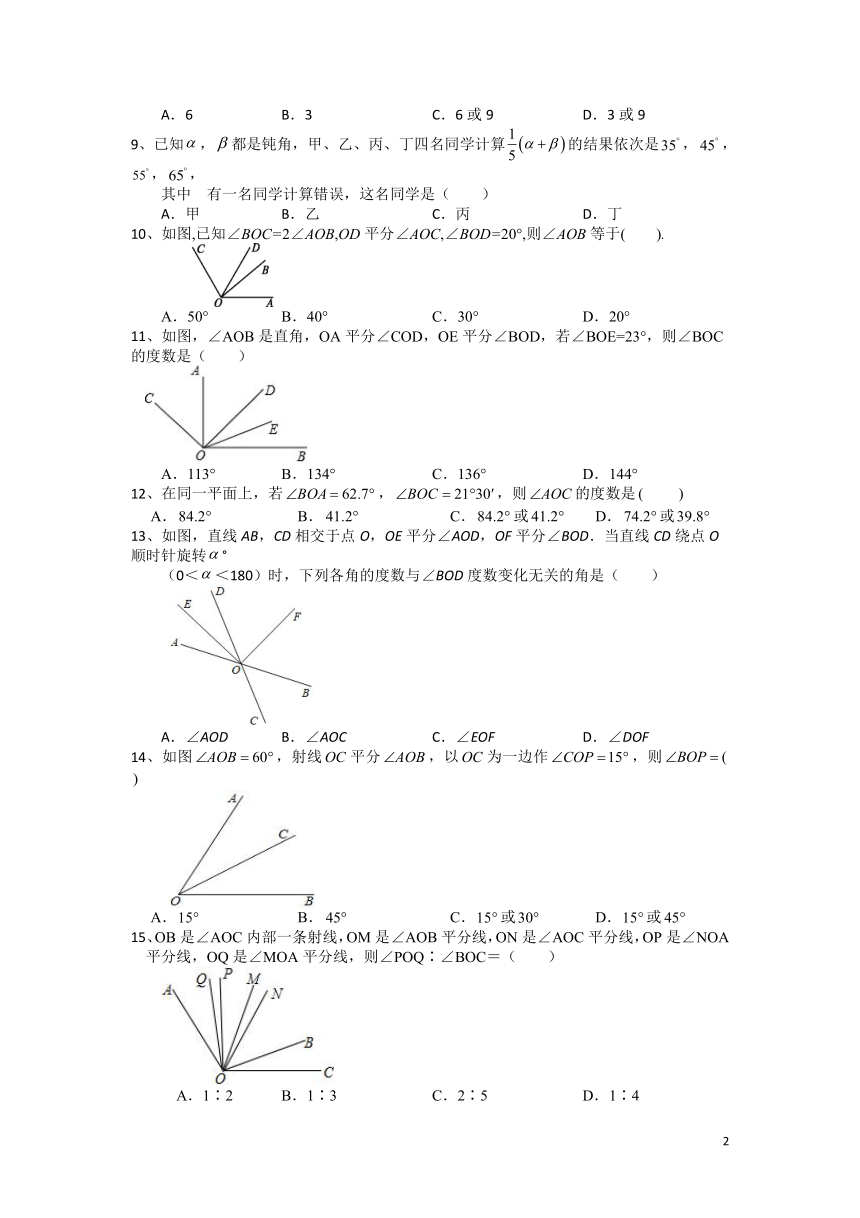
10、如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
A.50° B.40° C.30° D.20°
11、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
12、在同一平面上,若,,则的度数是
A. B. C.或 D.或
13、如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°
(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
14、如图,射线平分,以为一边作,则
A. B. C.或 D.或
15、OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )
A.1∶2 B.1∶3 C.2∶5 D.1∶4
二、填空题
16、如图,甲、乙两地之间有多条路可走,其中最短路线的走法序号是②④,其理由是 .
17、用度分秒表示:______;用度表示: =________
18、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
19、如图,已知线段AB和CD的公共部分,E、F分别为线段AB、CD的中点,EF=20,则AB的长为___________
20、如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
三、解答题
21、如图,已如A,B两点.
(1)画线段AB;
(2)延长线段AB到点C,使;
(3)反向延长线段AB到点D,使;
(4)点A,B分别是哪条线段的中点?若,请求出线段CD的长.
22、如图,已知、在线段上.
(1)图中共有 条线段;
(2)若.
①比较线段的大小: (填:“”、“ ”或“” ;
②若,,求的长.
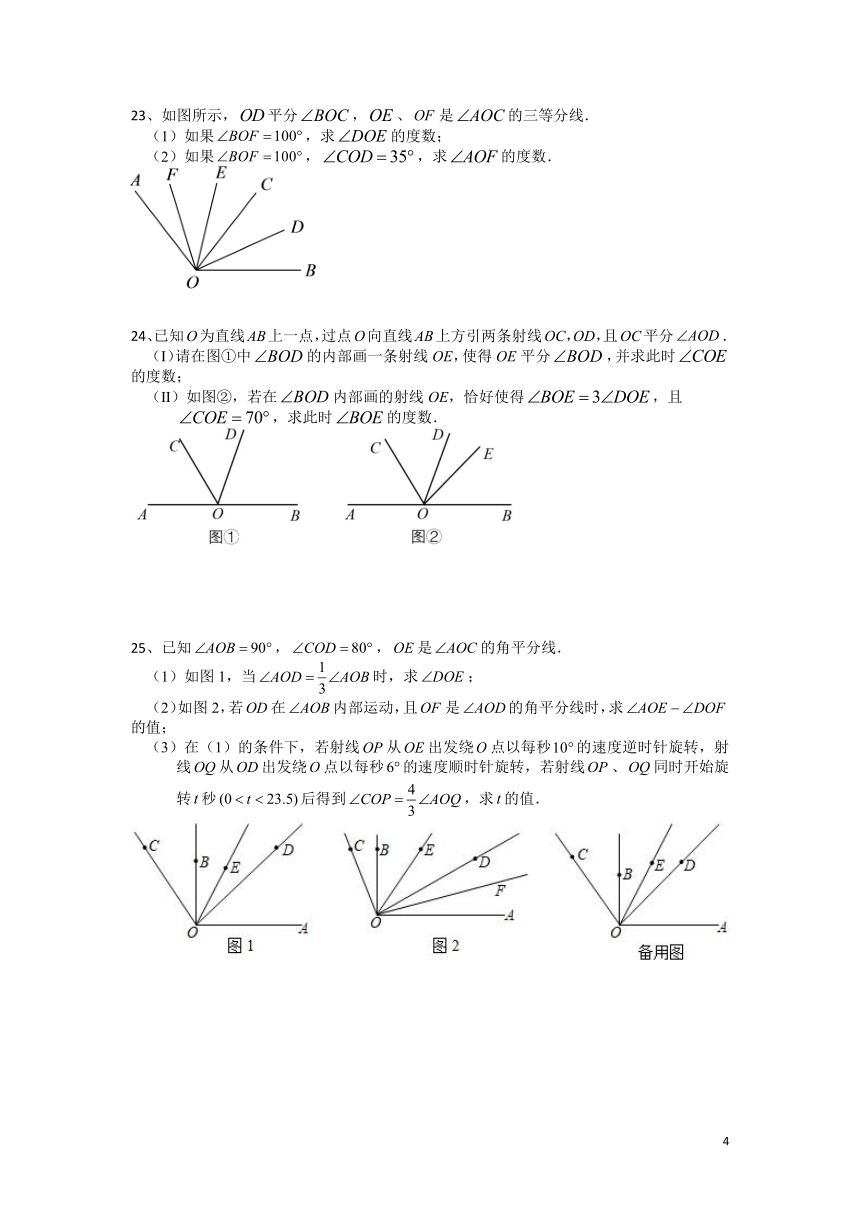
23、如图所示,平分,、是的三等分线.
(1)如果,求的度数;
(2)如果,,求的度数.
24、已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分.
(Ⅰ)请在图①中的内部画一条射线OE,使得OE平分,并求此时的度数;
(Ⅱ)如图②,若在内部画的射线OE,恰好使得,且,求此时的度数.
25、已知,,是的角平分线.
(1)如图1,当时,求;
(2)如图2,若在内部运动,且是的角平分线时,求的值;
(3)在(1)的条件下,若射线从出发绕点以每秒的速度逆时针旋转,射线从出发绕点以每秒的速度顺时针旋转,若射线、同时开始旋转秒后得到,求的值.
26、已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足
CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
阶段综合练(范围6.1线段、射线、直线~6.2角)
2021-2022学年苏科版七年级数学上册(解析)
一、选择题
1、在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( ).
A.①③ B.②③ C.③④ D.②④
【答案】C
【分析】
根据垂线段最短、直线和线段的性质即可得到结论.
【详解】
解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,依据的是两点之间线段最短;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,依据的是两点之间线段最短;
∴能用“两点之间,线段最短”的数学依据来解释的现象有:③④;
故选:C.
2、下列四个图形中,能用、、三种方法表示同一角的图形是( )
A.B.C. D.
【答案】B
【分析】
根据角的表示方法逐项判断即可得.
【详解】
A、、是同一个角,但不是,此项不符题意;
B、能用、、表示同一角,此项符合题意;
C、、是同一个角,但不是,此项不符题意;
D、图中、、分别表示三个不同的角,此项不符题意;
故选:B.
3、将化成度分秒表示,结果是( )
A. B. C. D.
【答案】B
【分析】
根据角的单位制换算法则即可得.
【详解】
故选:B.
4、下列说法中正确的是( )
A.8时45分,时针与分针的夹角是30° B.6时30分,时针与分针重合
C.3时30分,时针与分针的夹角是90° D.3时整,时针与分针的夹角是90°
【答案】D
【分析】
画出图形,利用钟表表盘的特征解答.分别计算出四个选项中时针和分针的夹角,进行判断即可.
【详解】
8时45分时,时针与分针的夹角是30°×=7.5°,故A选项错误,
6时30分时,时针在6和7的中间,分针在6的位置,时针与分针不重合,故B选项错误,
3时30分时,时针与分针的夹角为30°×2.5=75°,不为直角,故C选项错误,
3时整,时针与分针的夹角是90°
故选D.
5、对于题目:“如图1,已知A,B为两个海岛,点B在点A的正东方向,若灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,请画出灯塔C的位置.”甲、乙两人分别作出了如下解答:
甲:先以A为参照点,作南偏东25°,再以B为参照点,作南偏西65°,画出图形如图2.
乙:先以A为参照点,作东偏北25°,再以B为参照点,作西偏北55°,画出图形如图3.
下列判断正确的是( )
A.甲的说法和画图都正确 B.乙的说法正确,画图错误
C.乙的说法和画图都正确 D.甲乙的说法都错误
【解题思路】根据方向角定义即可进行判断.
【解答过程】解:根据方向角定义可知:
灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,画出灯塔C的位置如图3.
故选:D.
6、如图,已知D是线段中点,延长线段至C使,则下列结论中①:②;③;④;⑤;⑥,正确的有( )
A.①③④⑥ B.①②⑤⑥ C.①②③④ D.②③⑤⑥
【答案】B
【分析】
根据线段中点的定义即可得到结论.
【详解】
解:∵D是线段AB中点,
∴AB=2AD,故①正确;
∵BC=AB,
∴AC=2BC,故②正确;
∴,故③④错误;
∵D是线段AB中点,
∴,故⑤正确;
∵AC=2AB,AB=2BD,
∴AC=4BD,故⑥正确;
故选:B.
7、如图,是线段上两点,若且是的中点,则的长等于( )
A. B. C. D.
【答案】B
【分析】
首先求出线段CD,根据AC=2CD,求出AC即可解决问题.
【详解】
解:∵DB=7cm,CB=4cm,
∴CD=DB-CB=3cm,
∵D是AC的中点,
∴AC=2CD=6cm,
∴AB=AC+BC=10cm,
故选:B.
8、已知线段AB=6,C是直线AB上一点,BC=3,则线段AC长为( )
A.6 B.3 C.6或9 D.3或9
【答案】D
【分析】
本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意正确地画出图形解题.
【详解】
解:本题有两种情形:
①当点C在线段AB上时,如图1,
∵AC=AB-BC,
又∵AB=6,BC=3,
∴AC=6-3=3;
②当点C在线段AB的延长线上时,如图2,
∵AC=AB+BC,
又∵AB=6,BC=3,
∴AC=6+3=9.
综上可得:AC=3或9.
故选:D.
9、已知,都是钝角,甲、乙、丙、丁四名同学计算的结果依次是,,,,
其中 有一名同学计算错误,这名同学是( )
A.甲 B.乙 C.丙 D.丁
【答案】A
【分析】
根据钝角的概念进行解答,大于直角()小于平角()的角叫做钝角,求出的取值范围,然后作出判断.
【详解】
∵大于直角()小于平角()的角叫做钝角,
∴,,
∴,
∴,
∴不符合条件,
故选:A.
10、如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
A.50° B.40° C.30° D.20°
【答案】B
【分析】
由题意,根据角平分线的性质可知∠AOD= ∠COD=∠AOC ,根据角之间的等量关系∠BOC=2∠AOB ,∠BOC=∠COD+∠ BOD以及∠AOB=∠AOD- ∠BOD ,进行求解即可.
【详解】
因为OD平分∠AOC ,所以∠COD =∠AOD =∠AOC ;
又因为∠BOC=2∠AOB ,所以∠COD+∠BOD=2(∠AOD-∠BOD) ,
所以3∠BOD=2 ∠AOD-∠COD =∠AOD =∠COD ;
因为∠BOD=20°,所以∠AOB= ∠AOD- ∠BOD =2∠BOD =40°.
11、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
【答案】B
【分析】
首先根据OE平分∠BOD,∠BOE=23°,求出∠BOD的度数是多少;然后根据∠AOB是直角,求出∠AOD的度数,再根据OA平分∠COD,求出∠COD的度数,据此求出∠BOC的度数是多少即可.
【详解】
∵OE平分∠BOD,∠BOE=23°,
∴∠BOD=23°×2=46°;
∵∠AOB是直角,
∴∠AOD=90°-46°=44°,
又∵OA平分∠COD,
∴∠COD=2∠AOD=2×44°=88°,
∴∠BOC=∠BOD+∠COD=46°+88°=134°.
故选B.
12、在同一平面上,若,,则的度数是
A. B. C.或 D.或
【分析】根据角的和差,可得答案.
【解析】,
.
的度数是或.
故选:.
13、如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°
(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
【答案】C
【分析】
根据角平分线的定义可得∠AOD=2∠EOD,∠BOD=2∠DOF,结合平角的定义可求解∠EOF=90°,由∠EOF的度数为定值可判定求解.
【详解】
解:∵OE平分∠AOD,OF平分∠BOD,
∴∠AOD=2∠EOD,∠BOD=2∠DOF,
∵∠AOD+∠BOD=180°,
∴∠EOD+∠DOF=90°,即∠EOF=90°,
∴直线CD绕点O顺时针旋转α°(0<α<180)时,∠EOF的度数与∠BOD度数变化无关.
故选:C.
14、如图,射线平分,以为一边作,则
A. B. C.或 D.或
【分析】根据,射线平分,可得,分在内,在内,两种情况讨论求解即可.
【解析】,射线平分,
,
又
①当在内,
,
②当在内,
,
综上所述:或.
故选:.
15、OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )
A.1∶2 B.1∶3 C.2∶5 D.1∶4
【答案】D
【分析】
依据OM是∠AOB平分线,OQ是∠MOA平分线,可得∠AOQ=∠AOM=∠AOB,依据ON是∠AOC平分线,OP是∠NOA平分线,可得∠AOP=∠AON=∠AOC=(∠AOB+∠BOC),进而得出∠POQ:∠BOC=1:4.
【详解】
解:∵OM是∠AOB平分线,OQ是∠MOA平分线,
∴∠AOQ=∠AOM=∠AOB,
∵ON是∠AOC平分线,OP是∠NOA平分线,
∴∠AOP=∠AON=∠AOC=(∠AOB+∠BOC),
∴∠POQ=∠AOP-∠AOQ
=(∠AOB+∠BOC)-∠AOB,
=∠BOC,
∴∠POQ:∠BOC=1:4,
故选D.
二、填空题
16、如图,甲、乙两地之间有多条路可走,其中最短路线的走法序号是②④,其理由是 .
【分析】两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.根据线段的性质进行解答即可.
【解析】两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.即两点之间,线段最短.
故答案为:两点之间,线段最短.
17、用度分秒表示:______;用度表示: =________
【答案】 36.46°
【分析】
利用度、分、秒的换算即可,注意运算过程中秒的结果若满60,则转化为1分,分的结果若满60,则转化为1度.
【详解】
解:∵,,
∴;
∵,,
∴.
故答案为:;36.46°
18、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
【答案】75°
【分析】
依据OD是∠AOC的平分线,即可得到∠AOC=2∠COD=50°,再根据OC是∠AOB的平分线,即可得到∠BOC=∠AOC=50°,进而得出∠BOD=75°.
【详解】
解:∵OD是∠AOC的平分线,且∠COD=25°,
∴∠AOC=2∠COD=50°,
又∵OC是∠AOB的平分线,
∴∠BOC=∠AOC=50°,
∴∠BOD=∠BOC+∠COD=50°+25°=75°,
故答案为:75°.
19、如图,已知线段AB和CD的公共部分,E、F分别为线段AB、CD的中点,EF=20,则AB的长为___________
【答案】24
【分析】
(1)根据,可得AB,CD的长,根据线段和差,可得BC,AC的长,根据线段中点的性质,可得AE,CF的长,根据线段的和差,可得关于BD的方程,根据解方程,可得BD的值,即可求出AB的长度.
【详解】
解:(1)由,得
AB=3BD,CD=4BD,
由线段的和差,得
BC=CDBD=4BDBD=3BD,
AC=AB+BC=3BD+3BD=6BD.
由线段AB,CD的中点分别为E,F,得
,,
由线段的和差,得
EF=ACAECF,
即,
化简,得,
解得BD=8;
∴;
故答案为:24.
20、如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
【答案】15s或12s或24s
【分析】
由题意易得∠BON=6t°,∠MOA=3t°,则有OA与OB重合时,时间为t=20s,进而分①当OA与OB相遇前,又分当∠MON=2∠BON时和当∠AON=2∠BON时;②当OA与OB相遇后,∠AOM=2∠BOM,最后分类列方程进行求解即可.
【详解】
解:由题意得:∠BON=6t°,∠MOA=3t°,
∴当OA与OB重合时,则有,解得:,
∴①当OA与OB相遇前,即时,
当OB是∠MON的角平分线时,如图所示:
∵∠MON=180°,
∴,
∴,
当OB是∠AON的角平分线时,如图所示:
∴,
∵OB是∠AON的角平分线,
∴,
解得:;
②当OA与OB相遇后,即,
当OB是∠AOM的角平分线时,如图所示:
∴,
∵OB是∠AOM的角平分线,
∴,
解得:;
综上所述:以射线中两条为边组成一个角,使射线为该角的角平分线,此时的值为15s或12s或24s;
故答案为15s或12s或24s.
三、解答题
21、如图,已如A,B两点.
(1)画线段AB;
(2)延长线段AB到点C,使;
(3)反向延长线段AB到点D,使;
(4)点A,B分别是哪条线段的中点?若,请求出线段CD的长.
【答案】(1)见解析;(2)见解析;(3)见解析;(4)点A是线段BD的中点,点B是线段AC的中点;CD=9cm.
【分析】
(1)(2)(3)根据线段的定义和几何语言画出对应的几何图形;
(4)根据线段的中点的定义可判断点A是线段BD的中点;点B是线段AC的中点;然后利用CD=3AB求解.
【详解】
解:(1)如图,线段AB为所作;
(2)如图,点C为所作;
(3)如图,点D为所作;
(4)点A是线段BD的中点;点B是线段AC的中点;
所以(cm).
22、如图,已知、在线段上.
(1)图中共有 条线段;
(2)若.
①比较线段的大小: (填:“”、“ ”或“” ;
②若,,求的长.
【分析】(1)根据图形依次数出线段的条数即可;
(2)①根据等式的性质即可得到答案;
②依据线段的和差关系进行计算,即可得出的长;
【解析】(1)图中有线段:、、、、、,共6条,
故答案为:6.
(2)①,
,
即,
故答案为:.
②,,
,
,
,
,
23、如图所示,平分,、是的三等分线.
(1)如果,求的度数;
(2)如果,,求的度数.
【答案】(1);(2).
【分析】
(1)根据角平分线的定义及角的和差关系直接进行求解即可;
(2)由已知条件易得,然后可求解.
【详解】
解:(1)∵平分,、是的三等分线,
∴,,
∵,
∴即,
∴,
∴;
(2)∵、是的三等分线,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
24、已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分.
(Ⅰ)请在图①中的内部画一条射线OE,使得OE平分,并求此时的度数;
(Ⅱ)如图②,若在内部画的射线OE,恰好使得,且,求此时的度数.
【答案】(Ⅰ);(Ⅱ)的度数为.
【分析】
由角平分线的定义得出,,.
(2)设,则,,根据平角的定义列等式求出结果即可.
【详解】
(Ⅰ)如图,
∵OC平分,OE平分,
∴,,
∴.
(Ⅱ)如下图,设,
根据题意得.
∵,
∴.
∵OC平分,
∴,
∵,
∴.
解得:.∴.
∴的度数为.
25、已知,,是的角平分线.
(1)如图1,当时,求;
(2)如图2,若在内部运动,且是的角平分线时,求的值;
(3)在(1)的条件下,若射线从出发绕点以每秒的速度逆时针旋转,射线从出发绕点以每秒的速度顺时针旋转,若射线、同时开始旋转秒后得到,求的值.
【分析】(1)由题意得,再求出,即可得出答案;
(2)先由角平分线定义得,,再证,即可得出答案;
(3)分三种情况:①当射线、在内部时,即时,则,,由角的关系得,解得(舍去);
②当射线在外部时,射线在外部时,即时,由角的关系得,解得;
③当射线在外部时,即时,由角的关系得,解得.
【解析】(1),
,
,
,
平分,
,
;
(2)平分,
,
平分,
,
,
又,
;
(3)分三种情况:
①当射线、在内部时,即时,
由题意得:,,
,,
,
,
解得:(舍去);
②当射线在外部时,射线在外部时,即时,
则,,
,
解得:;
③当射线在外部时,即时,
则,,
,
解得:;
综上所述,的值为秒或秒.
26、已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足
CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
【答案】(1)4;(2)PQ是一个常数,即是常数m;(3)2AP+CQ﹣2PQ<1,见解析.
【分析】
(1)根据已知AB=6,CQ=2AQ,CP=2BP,以及线段的中点的定义解答;
(2)由题意根据已知条件AB=m(m为常数),CQ=2AQ,CP=2BP进行分析即可;
(3)根据题意,画出图形,求得2AP+CQ﹣2PQ=0,即可得出2AP+CQ﹣2PQ与1的大小关系.
【详解】
解:(1)∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵点C恰好在线段AB中点,
∴AC=BC=AB,
∵AB=6,
∴PQ=CQ+CP=AC+BC=×AB+×AB=×AB=×6=4;
故答案为:4;
(2)①点C在线段AB上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CQ+CP=AC+BC=×(AC+BC)=AB=m;
②点C在线段BA的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CP﹣CQ=BC﹣AC=×(BC﹣AC)=AB=m;
③点C在线段AB的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CQ﹣CP=AC﹣BC=×(AC﹣BC)=AB=m;
故PQ是一个常数,即是常数m;
(3)如图:
∵CQ=2AQ,
∴2AP+CQ﹣2PQ
=2AP+CQ﹣2(AP+AQ)
=2AP+CQ﹣2AP﹣2AQ
=CQ﹣2AQ
=2AQ﹣2AQ
=0,
∴2AP+CQ﹣2PQ<1.
2021-2022学年苏科版七年级数学上册
一、选择题
1、在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( ).
A.①③ B.②③ C.③④ D.②④
2、下列四个图形中,能用、、三种方法表示同一角的图形是( )
A.B.C. D.
3、将化成度分秒表示,结果是( )
A. B. C. D.
4、下列说法中正确的是( )
A.8时45分,时针与分针的夹角是30° B.6时30分,时针与分针重合
C.3时30分,时针与分针的夹角是90° D.3时整,时针与分针的夹角是90°
5、对于题目:“如图1,已知A,B为两个海岛,点B在点A的正东方向,若灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,请画出灯塔C的位置.”甲、乙两人分别作出了如下解答:
甲:先以A为参照点,作南偏东25°,再以B为参照点,作南偏西65°,画出图形如图2.
乙:先以A为参照点,作东偏北25°,再以B为参照点,作西偏北55°,画出图形如图3.
下列判断正确的是( )
A.甲的说法和画图都正确 B.乙的说法正确,画图错误
C.乙的说法和画图都正确 D.甲乙的说法都错误
6、如图,已知D是线段中点,延长线段至C使,则下列结论中①:②;③;④;⑤;⑥,正确的有( )
A.①③④⑥ B.①②⑤⑥ C.①②③④ D.②③⑤⑥
7、如图,是线段上两点,若且是的中点,则的长等于( )
A. B. C. D.
8、已知线段AB=6,C是直线AB上一点,BC=3,则线段AC长为( )
A.6 B.3 C.6或9 D.3或9
9、已知,都是钝角,甲、乙、丙、丁四名同学计算的结果依次是,,,,
其中 有一名同学计算错误,这名同学是( )
A.甲 B.乙 C.丙 D.丁
10、如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
A.50° B.40° C.30° D.20°
11、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
12、在同一平面上,若,,则的度数是
A. B. C.或 D.或
13、如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°
(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
14、如图,射线平分,以为一边作,则
A. B. C.或 D.或
15、OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )
A.1∶2 B.1∶3 C.2∶5 D.1∶4
二、填空题
16、如图,甲、乙两地之间有多条路可走,其中最短路线的走法序号是②④,其理由是 .
17、用度分秒表示:______;用度表示: =________
18、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
19、如图,已知线段AB和CD的公共部分,E、F分别为线段AB、CD的中点,EF=20,则AB的长为___________
20、如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
三、解答题
21、如图,已如A,B两点.
(1)画线段AB;
(2)延长线段AB到点C,使;
(3)反向延长线段AB到点D,使;
(4)点A,B分别是哪条线段的中点?若,请求出线段CD的长.
22、如图,已知、在线段上.
(1)图中共有 条线段;
(2)若.
①比较线段的大小: (填:“”、“ ”或“” ;
②若,,求的长.
23、如图所示,平分,、是的三等分线.
(1)如果,求的度数;
(2)如果,,求的度数.
24、已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分.
(Ⅰ)请在图①中的内部画一条射线OE,使得OE平分,并求此时的度数;
(Ⅱ)如图②,若在内部画的射线OE,恰好使得,且,求此时的度数.
25、已知,,是的角平分线.
(1)如图1,当时,求;
(2)如图2,若在内部运动,且是的角平分线时,求的值;
(3)在(1)的条件下,若射线从出发绕点以每秒的速度逆时针旋转,射线从出发绕点以每秒的速度顺时针旋转,若射线、同时开始旋转秒后得到,求的值.
26、已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足
CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
阶段综合练(范围6.1线段、射线、直线~6.2角)
2021-2022学年苏科版七年级数学上册(解析)
一、选择题
1、在下列生活实例中:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”的数学依据来解释的现象有( ).
A.①③ B.②③ C.③④ D.②④
【答案】C
【分析】
根据垂线段最短、直线和线段的性质即可得到结论.
【详解】
解:①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上,依据的是两点确定一条直线;
②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标,依据的是两点确定一条直线;
③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程,依据的是两点之间线段最短;
④从A地到B地架设电线,总是尽可能沿着线段AB架设,依据的是两点之间线段最短;
∴能用“两点之间,线段最短”的数学依据来解释的现象有:③④;
故选:C.
2、下列四个图形中,能用、、三种方法表示同一角的图形是( )
A.B.C. D.
【答案】B
【分析】
根据角的表示方法逐项判断即可得.
【详解】
A、、是同一个角,但不是,此项不符题意;
B、能用、、表示同一角,此项符合题意;
C、、是同一个角,但不是,此项不符题意;
D、图中、、分别表示三个不同的角,此项不符题意;
故选:B.
3、将化成度分秒表示,结果是( )
A. B. C. D.
【答案】B
【分析】
根据角的单位制换算法则即可得.
【详解】
故选:B.
4、下列说法中正确的是( )
A.8时45分,时针与分针的夹角是30° B.6时30分,时针与分针重合
C.3时30分,时针与分针的夹角是90° D.3时整,时针与分针的夹角是90°
【答案】D
【分析】
画出图形,利用钟表表盘的特征解答.分别计算出四个选项中时针和分针的夹角,进行判断即可.
【详解】
8时45分时,时针与分针的夹角是30°×=7.5°,故A选项错误,
6时30分时,时针在6和7的中间,分针在6的位置,时针与分针不重合,故B选项错误,
3时30分时,时针与分针的夹角为30°×2.5=75°,不为直角,故C选项错误,
3时整,时针与分针的夹角是90°
故选D.
5、对于题目:“如图1,已知A,B为两个海岛,点B在点A的正东方向,若灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,请画出灯塔C的位置.”甲、乙两人分别作出了如下解答:
甲:先以A为参照点,作南偏东25°,再以B为参照点,作南偏西65°,画出图形如图2.
乙:先以A为参照点,作东偏北25°,再以B为参照点,作西偏北55°,画出图形如图3.
下列判断正确的是( )
A.甲的说法和画图都正确 B.乙的说法正确,画图错误
C.乙的说法和画图都正确 D.甲乙的说法都错误
【解题思路】根据方向角定义即可进行判断.
【解答过程】解:根据方向角定义可知:
灯塔C在海岛A北偏东65°的方向上,在海岛B北偏西35°的方向上,画出灯塔C的位置如图3.
故选:D.
6、如图,已知D是线段中点,延长线段至C使,则下列结论中①:②;③;④;⑤;⑥,正确的有( )
A.①③④⑥ B.①②⑤⑥ C.①②③④ D.②③⑤⑥
【答案】B
【分析】
根据线段中点的定义即可得到结论.
【详解】
解:∵D是线段AB中点,
∴AB=2AD,故①正确;
∵BC=AB,
∴AC=2BC,故②正确;
∴,故③④错误;
∵D是线段AB中点,
∴,故⑤正确;
∵AC=2AB,AB=2BD,
∴AC=4BD,故⑥正确;
故选:B.
7、如图,是线段上两点,若且是的中点,则的长等于( )
A. B. C. D.
【答案】B
【分析】
首先求出线段CD,根据AC=2CD,求出AC即可解决问题.
【详解】
解:∵DB=7cm,CB=4cm,
∴CD=DB-CB=3cm,
∵D是AC的中点,
∴AC=2CD=6cm,
∴AB=AC+BC=10cm,
故选:B.
8、已知线段AB=6,C是直线AB上一点,BC=3,则线段AC长为( )
A.6 B.3 C.6或9 D.3或9
【答案】D
【分析】
本题没有给出图形,在画图时,应考虑到A、B、C三点之间的位置关系的多种可能,再根据题意正确地画出图形解题.
【详解】
解:本题有两种情形:
①当点C在线段AB上时,如图1,
∵AC=AB-BC,
又∵AB=6,BC=3,
∴AC=6-3=3;
②当点C在线段AB的延长线上时,如图2,
∵AC=AB+BC,
又∵AB=6,BC=3,
∴AC=6+3=9.
综上可得:AC=3或9.
故选:D.
9、已知,都是钝角,甲、乙、丙、丁四名同学计算的结果依次是,,,,
其中 有一名同学计算错误,这名同学是( )
A.甲 B.乙 C.丙 D.丁
【答案】A
【分析】
根据钝角的概念进行解答,大于直角()小于平角()的角叫做钝角,求出的取值范围,然后作出判断.
【详解】
∵大于直角()小于平角()的角叫做钝角,
∴,,
∴,
∴,
∴不符合条件,
故选:A.
10、如图,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=20°,则∠AOB等于( ).
A.50° B.40° C.30° D.20°
【答案】B
【分析】
由题意,根据角平分线的性质可知∠AOD= ∠COD=∠AOC ,根据角之间的等量关系∠BOC=2∠AOB ,∠BOC=∠COD+∠ BOD以及∠AOB=∠AOD- ∠BOD ,进行求解即可.
【详解】
因为OD平分∠AOC ,所以∠COD =∠AOD =∠AOC ;
又因为∠BOC=2∠AOB ,所以∠COD+∠BOD=2(∠AOD-∠BOD) ,
所以3∠BOD=2 ∠AOD-∠COD =∠AOD =∠COD ;
因为∠BOD=20°,所以∠AOB= ∠AOD- ∠BOD =2∠BOD =40°.
11、如图,∠AOB是直角,OA平分∠COD,OE平分∠BOD,若∠BOE=23°,则∠BOC的度数是( )
A.113° B.134° C.136° D.144°
【答案】B
【分析】
首先根据OE平分∠BOD,∠BOE=23°,求出∠BOD的度数是多少;然后根据∠AOB是直角,求出∠AOD的度数,再根据OA平分∠COD,求出∠COD的度数,据此求出∠BOC的度数是多少即可.
【详解】
∵OE平分∠BOD,∠BOE=23°,
∴∠BOD=23°×2=46°;
∵∠AOB是直角,
∴∠AOD=90°-46°=44°,
又∵OA平分∠COD,
∴∠COD=2∠AOD=2×44°=88°,
∴∠BOC=∠BOD+∠COD=46°+88°=134°.
故选B.
12、在同一平面上,若,,则的度数是
A. B. C.或 D.或
【分析】根据角的和差,可得答案.
【解析】,
.
的度数是或.
故选:.
13、如图,直线AB,CD相交于点O,OE平分∠AOD,OF平分∠BOD.当直线CD绕点O顺时针旋转°
(0<<180)时,下列各角的度数与∠BOD度数变化无关的角是( )
A.∠AOD B.∠AOC C.∠EOF D.∠DOF
【答案】C
【分析】
根据角平分线的定义可得∠AOD=2∠EOD,∠BOD=2∠DOF,结合平角的定义可求解∠EOF=90°,由∠EOF的度数为定值可判定求解.
【详解】
解:∵OE平分∠AOD,OF平分∠BOD,
∴∠AOD=2∠EOD,∠BOD=2∠DOF,
∵∠AOD+∠BOD=180°,
∴∠EOD+∠DOF=90°,即∠EOF=90°,
∴直线CD绕点O顺时针旋转α°(0<α<180)时,∠EOF的度数与∠BOD度数变化无关.
故选:C.
14、如图,射线平分,以为一边作,则
A. B. C.或 D.或
【分析】根据,射线平分,可得,分在内,在内,两种情况讨论求解即可.
【解析】,射线平分,
,
又
①当在内,
,
②当在内,
,
综上所述:或.
故选:.
15、OB是∠AOC内部一条射线,OM是∠AOB平分线,ON是∠AOC平分线,OP是∠NOA平分线,OQ是∠MOA平分线,则∠POQ∶∠BOC=( )
A.1∶2 B.1∶3 C.2∶5 D.1∶4
【答案】D
【分析】
依据OM是∠AOB平分线,OQ是∠MOA平分线,可得∠AOQ=∠AOM=∠AOB,依据ON是∠AOC平分线,OP是∠NOA平分线,可得∠AOP=∠AON=∠AOC=(∠AOB+∠BOC),进而得出∠POQ:∠BOC=1:4.
【详解】
解:∵OM是∠AOB平分线,OQ是∠MOA平分线,
∴∠AOQ=∠AOM=∠AOB,
∵ON是∠AOC平分线,OP是∠NOA平分线,
∴∠AOP=∠AON=∠AOC=(∠AOB+∠BOC),
∴∠POQ=∠AOP-∠AOQ
=(∠AOB+∠BOC)-∠AOB,
=∠BOC,
∴∠POQ:∠BOC=1:4,
故选D.
二、填空题
16、如图,甲、乙两地之间有多条路可走,其中最短路线的走法序号是②④,其理由是 .
【分析】两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.根据线段的性质进行解答即可.
【解析】两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.即两点之间,线段最短.
故答案为:两点之间,线段最短.
17、用度分秒表示:______;用度表示: =________
【答案】 36.46°
【分析】
利用度、分、秒的换算即可,注意运算过程中秒的结果若满60,则转化为1分,分的结果若满60,则转化为1度.
【详解】
解:∵,,
∴;
∵,,
∴.
故答案为:;36.46°
18、如图,OC是∠AOB的平分线,OD是∠AOC的平分线,且∠COD=25°,则∠BOD等于_____.
【答案】75°
【分析】
依据OD是∠AOC的平分线,即可得到∠AOC=2∠COD=50°,再根据OC是∠AOB的平分线,即可得到∠BOC=∠AOC=50°,进而得出∠BOD=75°.
【详解】
解:∵OD是∠AOC的平分线,且∠COD=25°,
∴∠AOC=2∠COD=50°,
又∵OC是∠AOB的平分线,
∴∠BOC=∠AOC=50°,
∴∠BOD=∠BOC+∠COD=50°+25°=75°,
故答案为:75°.
19、如图,已知线段AB和CD的公共部分,E、F分别为线段AB、CD的中点,EF=20,则AB的长为___________
【答案】24
【分析】
(1)根据,可得AB,CD的长,根据线段和差,可得BC,AC的长,根据线段中点的性质,可得AE,CF的长,根据线段的和差,可得关于BD的方程,根据解方程,可得BD的值,即可求出AB的长度.
【详解】
解:(1)由,得
AB=3BD,CD=4BD,
由线段的和差,得
BC=CDBD=4BDBD=3BD,
AC=AB+BC=3BD+3BD=6BD.
由线段AB,CD的中点分别为E,F,得
,,
由线段的和差,得
EF=ACAECF,
即,
化简,得,
解得BD=8;
∴;
故答案为:24.
20、如图,点依次在直线上,射线绕点O以每秒的速度顺时针旋转,同时射线绕点O以每秒的速度逆时针旋转,直线保持不动,设旋转时间为t秒,现以射线中两条为边组成一个角,使射线为该角的角平分线,此时t的值为_______.
【答案】15s或12s或24s
【分析】
由题意易得∠BON=6t°,∠MOA=3t°,则有OA与OB重合时,时间为t=20s,进而分①当OA与OB相遇前,又分当∠MON=2∠BON时和当∠AON=2∠BON时;②当OA与OB相遇后,∠AOM=2∠BOM,最后分类列方程进行求解即可.
【详解】
解:由题意得:∠BON=6t°,∠MOA=3t°,
∴当OA与OB重合时,则有,解得:,
∴①当OA与OB相遇前,即时,
当OB是∠MON的角平分线时,如图所示:
∵∠MON=180°,
∴,
∴,
当OB是∠AON的角平分线时,如图所示:
∴,
∵OB是∠AON的角平分线,
∴,
解得:;
②当OA与OB相遇后,即,
当OB是∠AOM的角平分线时,如图所示:
∴,
∵OB是∠AOM的角平分线,
∴,
解得:;
综上所述:以射线中两条为边组成一个角,使射线为该角的角平分线,此时的值为15s或12s或24s;
故答案为15s或12s或24s.
三、解答题
21、如图,已如A,B两点.
(1)画线段AB;
(2)延长线段AB到点C,使;
(3)反向延长线段AB到点D,使;
(4)点A,B分别是哪条线段的中点?若,请求出线段CD的长.
【答案】(1)见解析;(2)见解析;(3)见解析;(4)点A是线段BD的中点,点B是线段AC的中点;CD=9cm.
【分析】
(1)(2)(3)根据线段的定义和几何语言画出对应的几何图形;
(4)根据线段的中点的定义可判断点A是线段BD的中点;点B是线段AC的中点;然后利用CD=3AB求解.
【详解】
解:(1)如图,线段AB为所作;
(2)如图,点C为所作;
(3)如图,点D为所作;
(4)点A是线段BD的中点;点B是线段AC的中点;
所以(cm).
22、如图,已知、在线段上.
(1)图中共有 条线段;
(2)若.
①比较线段的大小: (填:“”、“ ”或“” ;
②若,,求的长.
【分析】(1)根据图形依次数出线段的条数即可;
(2)①根据等式的性质即可得到答案;
②依据线段的和差关系进行计算,即可得出的长;
【解析】(1)图中有线段:、、、、、,共6条,
故答案为:6.
(2)①,
,
即,
故答案为:.
②,,
,
,
,
,
23、如图所示,平分,、是的三等分线.
(1)如果,求的度数;
(2)如果,,求的度数.
【答案】(1);(2).
【分析】
(1)根据角平分线的定义及角的和差关系直接进行求解即可;
(2)由已知条件易得,然后可求解.
【详解】
解:(1)∵平分,、是的三等分线,
∴,,
∵,
∴即,
∴,
∴;
(2)∵、是的三等分线,
∴,
∵,平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴.
24、已知O为直线AB上一点,过点O向直线AB上方引两条射线OC,OD,且OC平分.
(Ⅰ)请在图①中的内部画一条射线OE,使得OE平分,并求此时的度数;
(Ⅱ)如图②,若在内部画的射线OE,恰好使得,且,求此时的度数.
【答案】(Ⅰ);(Ⅱ)的度数为.
【分析】
由角平分线的定义得出,,.
(2)设,则,,根据平角的定义列等式求出结果即可.
【详解】
(Ⅰ)如图,
∵OC平分,OE平分,
∴,,
∴.
(Ⅱ)如下图,设,
根据题意得.
∵,
∴.
∵OC平分,
∴,
∵,
∴.
解得:.∴.
∴的度数为.
25、已知,,是的角平分线.
(1)如图1,当时,求;
(2)如图2,若在内部运动,且是的角平分线时,求的值;
(3)在(1)的条件下,若射线从出发绕点以每秒的速度逆时针旋转,射线从出发绕点以每秒的速度顺时针旋转,若射线、同时开始旋转秒后得到,求的值.
【分析】(1)由题意得,再求出,即可得出答案;
(2)先由角平分线定义得,,再证,即可得出答案;
(3)分三种情况:①当射线、在内部时,即时,则,,由角的关系得,解得(舍去);
②当射线在外部时,射线在外部时,即时,由角的关系得,解得;
③当射线在外部时,即时,由角的关系得,解得.
【解析】(1),
,
,
,
平分,
,
;
(2)平分,
,
平分,
,
,
又,
;
(3)分三种情况:
①当射线、在内部时,即时,
由题意得:,,
,,
,
,
解得:(舍去);
②当射线在外部时,射线在外部时,即时,
则,,
,
解得:;
③当射线在外部时,即时,
则,,
,
解得:;
综上所述,的值为秒或秒.
26、已知线段AB=m(m为常数),点C为直线AB上一点,点P、Q分别在线段BC、AC上,且满足
CQ=2AQ,CP=2BP.
(1)如图,若AB=6,当点C恰好在线段AB中点时,则PQ= ;
(2)若点C为直线AB上任一点,则PQ长度是否为常数?若是,请求出这个常数;若不是,请说明理由;
(3)若点C在点A左侧,同时点P在线段AB上(不与端点重合),请判断2AP+CQ﹣2PQ与1的大小关系,并说明理由.
【答案】(1)4;(2)PQ是一个常数,即是常数m;(3)2AP+CQ﹣2PQ<1,见解析.
【分析】
(1)根据已知AB=6,CQ=2AQ,CP=2BP,以及线段的中点的定义解答;
(2)由题意根据已知条件AB=m(m为常数),CQ=2AQ,CP=2BP进行分析即可;
(3)根据题意,画出图形,求得2AP+CQ﹣2PQ=0,即可得出2AP+CQ﹣2PQ与1的大小关系.
【详解】
解:(1)∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵点C恰好在线段AB中点,
∴AC=BC=AB,
∵AB=6,
∴PQ=CQ+CP=AC+BC=×AB+×AB=×AB=×6=4;
故答案为:4;
(2)①点C在线段AB上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CQ+CP=AC+BC=×(AC+BC)=AB=m;
②点C在线段BA的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CP﹣CQ=BC﹣AC=×(BC﹣AC)=AB=m;
③点C在线段AB的延长线上:
∵CQ=2AQ,CP=2BP,
∴CQ=AC,CP=BC,
∵AB=m(m为常数),
∴PQ=CQ﹣CP=AC﹣BC=×(AC﹣BC)=AB=m;
故PQ是一个常数,即是常数m;
(3)如图:
∵CQ=2AQ,
∴2AP+CQ﹣2PQ
=2AP+CQ﹣2(AP+AQ)
=2AP+CQ﹣2AP﹣2AQ
=CQ﹣2AQ
=2AQ﹣2AQ
=0,
∴2AP+CQ﹣2PQ<1.
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
