4.3 非数值计算【新教材】2021-2022学年教科版(2019)高中信息技术必修一 课件(23张PPT+视频)
文档属性
| 名称 | 4.3 非数值计算【新教材】2021-2022学年教科版(2019)高中信息技术必修一 课件(23张PPT+视频) |

|
|
| 格式 | pptx | ||
| 文件大小 | 29.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 教科版(2019) | ||
| 科目 | 信息技术(信息科技) | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第2单元 编程计算
第1单元 初识数据与计算
第3单元 认识数据
第4单元 计算与问题解决
第5单元 数据分析与人工智能
信息技术
(必修1)
4.3 非数值计算
学习目标
★ 运用合适的算法形成解决问题的方案。
★ 了解算法设计中的分治思想,并运用二分查找解决实际问题。
★ 体验递归算法,并结合具体问题开展编程实践。
在数值计算中,我们更多考虑的是“数” ,但计算应该是一个更广泛的领域。计算的对象可以是自然界和人类社会的一切事物。更确切地说,计算的对象可以是某些信息,如数据、文字、语言、图形、知识、事物的运动过程及思维过程。如果说数值计算主要探讨数学问题的话,那么非数值计算更多探讨" 算法” 问题。
许多程序设计问题的解决,要依靠标准算法和现成的模型,更需要编程者开阔思路,提出一些新颖、巧妙的算法,或者设计出一些独特的数据结构来支撑和实现算法。在解决非数值类计算问题时,一些基础的思维方式可以借鉴,如分治、递归、解析等。
新课导入
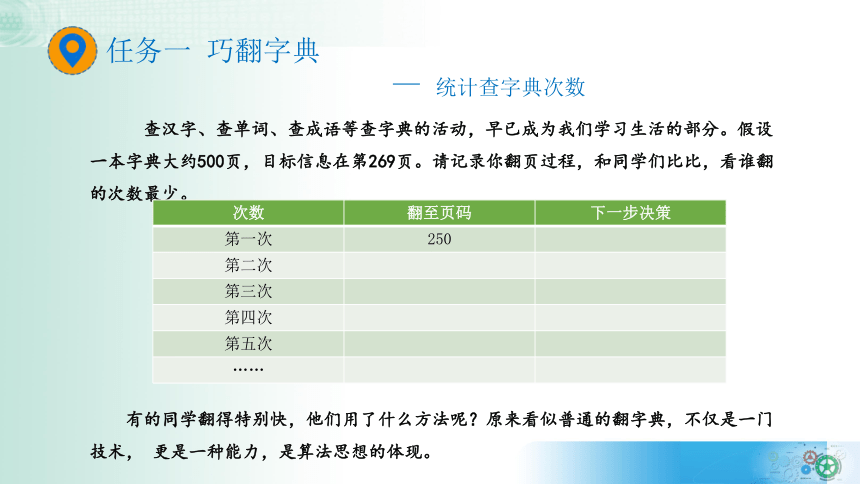
任务一 巧翻字典
— 统计查字典次数
查汉字、查单词、查成语等查字典的活动,早已成为我们学习生活的部分。假设一本字典大约500页,目标信息在第269页。请记录你翻页过程,和同学们比比,看谁翻的次数最少。
次数 翻至页码 下一步决策
第一次 250
第二次
第三次
第四次
第五次
……
有的同学翻得特别快,他们用了什么方法呢?原来看似普通的翻字典,不仅是一门技术, 更是一种能力,是算法思想的体现。
凡治众如治寡,分数是也。
——《孙子兵法》
B
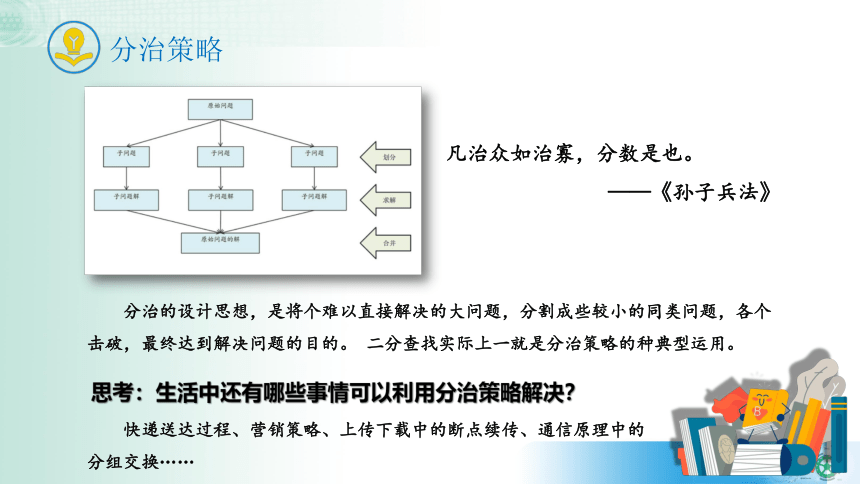
思考:生活中还有哪些事情可以利用分治策略解决?
快递送达过程、营销策略、上传下载中的断点续传、通信原理中的分组交换……
分治策略
分治的设计思想,是将个难以直接解决的大问题,分割成些较小的同类问题,各个击破,最终达到解决问题的目的。 二分查找实际上一就是分治策略的种典型运用。
二分思想:将数列有序排列,采用跳跃的方式查找数据。
方法:以递增数列为例,以中点位置元素作为比较对象,若要查找元素值小于该中点元素,将待查找序列缩小为左半部分,否则为右半部分。每次比较后都能将查找区间缩小一半。
找一半
按照顺序找一半,
一比较,舍一半。
继续找一半,
一半又一半,
快速找答案!
二分查找
二分查找法是一种高效的查找方法。它可以明显减少比较次数,提高查找效率。在一个有n个元素的有序序列中,利用二分查找大约需要log2n次。但是,二分法查找的前提条件是被查找的数据必须是有序的。
查找的基本算法有:顺序查找、二分查找、分块查找、哈希查找等。
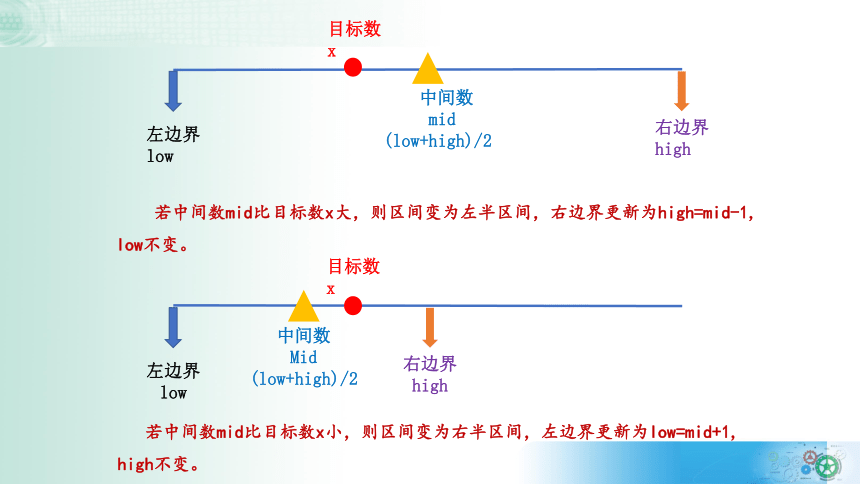
左边界
low
右边界
high
目标数
x
中间数
mid
(low+high)/2
若中间数mid比目标数x大,则区间变为左半区间,右边界更新为high=mid-1, low不变。
左边界
low
右边界
high
目标数
x
中间数
Mid
(low+high)/2
若中间数mid比目标数x小,则区间变为右半区间,左边界更新为low=mid+1, high不变。
例:
在翻页过程中借助两个书签,划定目标所属范围,然后翻到两个书签的中间位置。每次目标区域都更新为原来的“二分之一”,当数据范围缩小到只有1个数的时候肯定能得到问题的解。1000以内的页码,最多翻10次肯定能找到解。
目标信息在第269页。
第0页
第1000页
第0页
第500页
第250页
第500页
第250页
第375页
第250页
第312页
有了翻字典的实际操作经验,我们来尝试完善下面的二分查找程序。
x=int(input(“请输入要查找的数据:"))
step=0 #记录查找次数
flagl=l #目标区域左边界
flag2=1000 #目标区域右边界
while(flag1<=flag2) #区间数据范围小于1则结束循环
mid=(flag1+flag2)/2 #中间值
step=step+1 #查找次数加1
if mid>x:
flag2=mid-1 #有边界前移
elif midflag1=mid+1 #左边界后移
else:
break #恰好找到目标数据, 退出循环
print(“查询次数为:”,step) #输出次数
如果输入的数据不在范围内,会出现什么结果呢?程序还需要在哪些地方进行完善?大家一起来试试吧。
x=int(input(“请输入要查找的数据:"))
step=0 #记录查找次数
flag1=1 #目标区域左边界
flag2=1000 #目标区域右边界
if x>flag2 or xwhile(flag2-flag1>1): #区间数据范围小于1则结束循环
mid=(flag1+flag2)/2 #中间值
step=step+1 #查找次数加1
if mid>x:
flag2=mid #有边界前移
elif midflag1=mid #左边界后移
else:
break #恰好找到目标数据, 退出循环
print(“查询次数为:”,step) #输出次数
else:
print(“查询超出范围。”)
任务二 玩转“汉诺塔”游戏
——剖析问题,设计游戏策略
“汉诺塔”游戏源于 一个古老的印度传说。 如图所示,木板上有A、B、C三根杆, A杆上有若干木盘,规定每次移动一个木盘,且小的木盘只能叠在大的木盘上面。 请设计算法,用尽可能少的次数把所有木盘从A杆移动到C杆上。
要使移动次数尽可能少,必须排除无效移动。现在让我们来观察一下移动过程。
递归
直接或间接地调用自身的方法称为递归。可以将递归简单类比为具有自相似性重复的事物。
在数学与计算机领域中,递归函数是指用函数自身来定义该函数的方法。如著名的斐波那契数列 “1, 1, 2, 3, 5, 8, 13,…”,可以递归定义为:
递归是计算科学领域中一种重要的计算思维模式。它既是一种抽象表达的手段,也是一种问题求解的重要方法。
F(n)=
1(n=1或n=2)
F(n-1)+F(n-2)(n>2)
递归的基本思想
递归的基本思想是把规模较大的问题层层转化为规模较小的同类问题求解。对递归而言,递推与回归,二者缺一不可。
递归可用“分”,“治”,“合”三个字概括
1)分:将原有问题分解成K个子问题。
2)治:对这K个子问题分别求解。如果子问题的规模仍然不够小,则将其再分解为K个子问题,如此进 行下去,直到问题足够小时,就很容易求出子问题的解。
3)合:将求出的小规模问题的解合并为一个更大规模问题的解,自下而上逐步求出原问题的解。
递推关系是递归的重要组成,而边界条件是递归的另一要素,它保证递归能在有限次的计算后得出结果,而不会产生尤限循环的情况。
移动3个木盘的方法是:根据木盘叠放规则,要使A杆上最大的木盘(记为x)移动到C杆上(子问题1, 如图第4步),必须先把 x上方的所有木盘移动到B杆上(子问题2, 如图4中的前3步),然后再将B杆上所有的木盘移动到C杆上(子问题3, 如图中的后3步)。
第1步:A→C
第2步:A→B
第3步:C→B
第4步:A→C
第5步:B→A
第6步:B→C
第7步:A→C
3个木盘的移动问题成功解决了,就可以解决更多木盘的移动问题了。
解决移动3个木盘的问题。
解决移动n个木盘的问题。
将n个木盘从A杆移动到C杆,需要借助中间的B杆。只要超过一个木盘,在移动过程中,总会存在起始杆、 过渡杆及目标杆的问题。因此,定义函数时,用到了4个参数:hanoi(n,A,B,C), n表示需要移动的盘子数量,A表示盘子的起始杆,B表示中间过渡杆,C表示目标杆,如图所示。
活动 代码实现汉诺塔游戏
def hanno(n,s,m,t):
#定义一个函数,n层塔,将盘子从s借助m移动到t
if n==1:
print(s,'-->',t) #将一个盘子从s移动到t
else:
hanno(n-1,s,t,m) #将前n-1个盘子从s移动到m上
print(s,'-->',t) #将最底下的最后一个盘子从s移动到t上
hanno(n-1,m,s,t) #将m上的n-1个盘子移动到t上
#主程序
n=int(input('请输入汉诺塔的层数:'))
hanno(n,'A','B','C')
input("运行完毕,请按回车键退出...")
迭代与递归的关系
迭代算法与递归算法都需要重复执行某些代码,两者既有区别又有密切的联系。
递归 迭代
重复方式是重复调用函数自身。 重复方式:是重复反馈过程的活动,其目的通常是逼近所需目标或结果。
结束方式:遇到满足终止条件的情况时逐层返回。 结束方式:通常使用计数器结束循环。
迭代程序可以转换成等价的递归程序。以上一节中的计算斐波那契数列第n项的值为例,程序间的转换如下:
1、计算“汉诺塔”游戏移动的次数。
参考答案:
def f(n):
if n==0:
return 0
else:
return 2*f(n-1)+1
x=int(input("请输入塔的个数:"))
print("需要移动",f(x),"次")
input("运行完毕,请按回车键退出...")
巩固提升
练一练
2、尝试用二分法求解x3-x2+x-1=0
操作提示:
令f(x)= x3-x2+x-1,针对有解的单调区间(a,b),
取x。=(a+b)/2:
若f(a)*f(x。)<0,则f(x)在(a,x。)内有解;
若f(x。)*f(b)< 0,则f(x)在(x。,b)内有解;
若|f(x。)|<10-6,则x。为方程的解。
参考答案:
def f(x):
#定义方程
return x**3-x**2+x-1
a=float(input("请输入解区间的左边界:"))
b=float(input("请输入解区间的右边界:"))
while abs(b-a)>1e-6:
x0=(a+b)/2
if f(a)*f(x0)<0:
b=x0
if f(b)*f(x0)<0:
a=x0
if f(x0)==0:
break
print("解为:",x0)
input("运行完毕,请按回车键退出...")
课堂小结
非数值计算
递归:直接或间接地调用自身的方法称为递归。
递归函数是指用函数自身来定义该函数的方法。
递推关系是递归的重要组成, 而边界条件是递归的另一要素, 它保证递归能在有限次的计算后得出结果, 而不会产生尤限循环的情况。
分治策略
二分查找
将一个难以直接解决的大问题,分割成一些较小的同类问题,各个击破 。
二分查找又叫折半查找, 该方法主要将数列有序排列, 采用跳跃式的方式查找数据。
二分法查找的前提条件是被查找的数据必须是有序的。
分:原问题分解成若干子问题
治:对子问题分别求解
合:子问题的解合并成原问题的解
第2单元 编程计算
第1单元 初识数据与计算
第3单元 认识数据
第4单元 计算与问题解决
第5单元 数据分析与人工智能
信息技术
(必修1)
4.3 非数值计算
学习目标
★ 运用合适的算法形成解决问题的方案。
★ 了解算法设计中的分治思想,并运用二分查找解决实际问题。
★ 体验递归算法,并结合具体问题开展编程实践。
在数值计算中,我们更多考虑的是“数” ,但计算应该是一个更广泛的领域。计算的对象可以是自然界和人类社会的一切事物。更确切地说,计算的对象可以是某些信息,如数据、文字、语言、图形、知识、事物的运动过程及思维过程。如果说数值计算主要探讨数学问题的话,那么非数值计算更多探讨" 算法” 问题。
许多程序设计问题的解决,要依靠标准算法和现成的模型,更需要编程者开阔思路,提出一些新颖、巧妙的算法,或者设计出一些独特的数据结构来支撑和实现算法。在解决非数值类计算问题时,一些基础的思维方式可以借鉴,如分治、递归、解析等。
新课导入
任务一 巧翻字典
— 统计查字典次数
查汉字、查单词、查成语等查字典的活动,早已成为我们学习生活的部分。假设一本字典大约500页,目标信息在第269页。请记录你翻页过程,和同学们比比,看谁翻的次数最少。
次数 翻至页码 下一步决策
第一次 250
第二次
第三次
第四次
第五次
……
有的同学翻得特别快,他们用了什么方法呢?原来看似普通的翻字典,不仅是一门技术, 更是一种能力,是算法思想的体现。
凡治众如治寡,分数是也。
——《孙子兵法》
B
思考:生活中还有哪些事情可以利用分治策略解决?
快递送达过程、营销策略、上传下载中的断点续传、通信原理中的分组交换……
分治策略
分治的设计思想,是将个难以直接解决的大问题,分割成些较小的同类问题,各个击破,最终达到解决问题的目的。 二分查找实际上一就是分治策略的种典型运用。
二分思想:将数列有序排列,采用跳跃的方式查找数据。
方法:以递增数列为例,以中点位置元素作为比较对象,若要查找元素值小于该中点元素,将待查找序列缩小为左半部分,否则为右半部分。每次比较后都能将查找区间缩小一半。
找一半
按照顺序找一半,
一比较,舍一半。
继续找一半,
一半又一半,
快速找答案!
二分查找
二分查找法是一种高效的查找方法。它可以明显减少比较次数,提高查找效率。在一个有n个元素的有序序列中,利用二分查找大约需要log2n次。但是,二分法查找的前提条件是被查找的数据必须是有序的。
查找的基本算法有:顺序查找、二分查找、分块查找、哈希查找等。
左边界
low
右边界
high
目标数
x
中间数
mid
(low+high)/2
若中间数mid比目标数x大,则区间变为左半区间,右边界更新为high=mid-1, low不变。
左边界
low
右边界
high
目标数
x
中间数
Mid
(low+high)/2
若中间数mid比目标数x小,则区间变为右半区间,左边界更新为low=mid+1, high不变。
例:
在翻页过程中借助两个书签,划定目标所属范围,然后翻到两个书签的中间位置。每次目标区域都更新为原来的“二分之一”,当数据范围缩小到只有1个数的时候肯定能得到问题的解。1000以内的页码,最多翻10次肯定能找到解。
目标信息在第269页。
第0页
第1000页
第0页
第500页
第250页
第500页
第250页
第375页
第250页
第312页
有了翻字典的实际操作经验,我们来尝试完善下面的二分查找程序。
x=int(input(“请输入要查找的数据:"))
step=0 #记录查找次数
flagl=l #目标区域左边界
flag2=1000 #目标区域右边界
while(flag1<=flag2) #区间数据范围小于1则结束循环
mid=(flag1+flag2)/2 #中间值
step=step+1 #查找次数加1
if mid>x:
flag2=mid-1 #有边界前移
elif mid
else:
break #恰好找到目标数据, 退出循环
print(“查询次数为:”,step) #输出次数
如果输入的数据不在范围内,会出现什么结果呢?程序还需要在哪些地方进行完善?大家一起来试试吧。
x=int(input(“请输入要查找的数据:"))
step=0 #记录查找次数
flag1=1 #目标区域左边界
flag2=1000 #目标区域右边界
if x>flag2 or x
mid=(flag1+flag2)/2 #中间值
step=step+1 #查找次数加1
if mid>x:
flag2=mid #有边界前移
elif mid
else:
break #恰好找到目标数据, 退出循环
print(“查询次数为:”,step) #输出次数
else:
print(“查询超出范围。”)
任务二 玩转“汉诺塔”游戏
——剖析问题,设计游戏策略
“汉诺塔”游戏源于 一个古老的印度传说。 如图所示,木板上有A、B、C三根杆, A杆上有若干木盘,规定每次移动一个木盘,且小的木盘只能叠在大的木盘上面。 请设计算法,用尽可能少的次数把所有木盘从A杆移动到C杆上。
要使移动次数尽可能少,必须排除无效移动。现在让我们来观察一下移动过程。
递归
直接或间接地调用自身的方法称为递归。可以将递归简单类比为具有自相似性重复的事物。
在数学与计算机领域中,递归函数是指用函数自身来定义该函数的方法。如著名的斐波那契数列 “1, 1, 2, 3, 5, 8, 13,…”,可以递归定义为:
递归是计算科学领域中一种重要的计算思维模式。它既是一种抽象表达的手段,也是一种问题求解的重要方法。
F(n)=
1(n=1或n=2)
F(n-1)+F(n-2)(n>2)
递归的基本思想
递归的基本思想是把规模较大的问题层层转化为规模较小的同类问题求解。对递归而言,递推与回归,二者缺一不可。
递归可用“分”,“治”,“合”三个字概括
1)分:将原有问题分解成K个子问题。
2)治:对这K个子问题分别求解。如果子问题的规模仍然不够小,则将其再分解为K个子问题,如此进 行下去,直到问题足够小时,就很容易求出子问题的解。
3)合:将求出的小规模问题的解合并为一个更大规模问题的解,自下而上逐步求出原问题的解。
递推关系是递归的重要组成,而边界条件是递归的另一要素,它保证递归能在有限次的计算后得出结果,而不会产生尤限循环的情况。
移动3个木盘的方法是:根据木盘叠放规则,要使A杆上最大的木盘(记为x)移动到C杆上(子问题1, 如图第4步),必须先把 x上方的所有木盘移动到B杆上(子问题2, 如图4中的前3步),然后再将B杆上所有的木盘移动到C杆上(子问题3, 如图中的后3步)。
第1步:A→C
第2步:A→B
第3步:C→B
第4步:A→C
第5步:B→A
第6步:B→C
第7步:A→C
3个木盘的移动问题成功解决了,就可以解决更多木盘的移动问题了。
解决移动3个木盘的问题。
解决移动n个木盘的问题。
将n个木盘从A杆移动到C杆,需要借助中间的B杆。只要超过一个木盘,在移动过程中,总会存在起始杆、 过渡杆及目标杆的问题。因此,定义函数时,用到了4个参数:hanoi(n,A,B,C), n表示需要移动的盘子数量,A表示盘子的起始杆,B表示中间过渡杆,C表示目标杆,如图所示。
活动 代码实现汉诺塔游戏
def hanno(n,s,m,t):
#定义一个函数,n层塔,将盘子从s借助m移动到t
if n==1:
print(s,'-->',t) #将一个盘子从s移动到t
else:
hanno(n-1,s,t,m) #将前n-1个盘子从s移动到m上
print(s,'-->',t) #将最底下的最后一个盘子从s移动到t上
hanno(n-1,m,s,t) #将m上的n-1个盘子移动到t上
#主程序
n=int(input('请输入汉诺塔的层数:'))
hanno(n,'A','B','C')
input("运行完毕,请按回车键退出...")
迭代与递归的关系
迭代算法与递归算法都需要重复执行某些代码,两者既有区别又有密切的联系。
递归 迭代
重复方式是重复调用函数自身。 重复方式:是重复反馈过程的活动,其目的通常是逼近所需目标或结果。
结束方式:遇到满足终止条件的情况时逐层返回。 结束方式:通常使用计数器结束循环。
迭代程序可以转换成等价的递归程序。以上一节中的计算斐波那契数列第n项的值为例,程序间的转换如下:
1、计算“汉诺塔”游戏移动的次数。
参考答案:
def f(n):
if n==0:
return 0
else:
return 2*f(n-1)+1
x=int(input("请输入塔的个数:"))
print("需要移动",f(x),"次")
input("运行完毕,请按回车键退出...")
巩固提升
练一练
2、尝试用二分法求解x3-x2+x-1=0
操作提示:
令f(x)= x3-x2+x-1,针对有解的单调区间(a,b),
取x。=(a+b)/2:
若f(a)*f(x。)<0,则f(x)在(a,x。)内有解;
若f(x。)*f(b)< 0,则f(x)在(x。,b)内有解;
若|f(x。)|<10-6,则x。为方程的解。
参考答案:
def f(x):
#定义方程
return x**3-x**2+x-1
a=float(input("请输入解区间的左边界:"))
b=float(input("请输入解区间的右边界:"))
while abs(b-a)>1e-6:
x0=(a+b)/2
if f(a)*f(x0)<0:
b=x0
if f(b)*f(x0)<0:
a=x0
if f(x0)==0:
break
print("解为:",x0)
input("运行完毕,请按回车键退出...")
课堂小结
非数值计算
递归:直接或间接地调用自身的方法称为递归。
递归函数是指用函数自身来定义该函数的方法。
递推关系是递归的重要组成, 而边界条件是递归的另一要素, 它保证递归能在有限次的计算后得出结果, 而不会产生尤限循环的情况。
分治策略
二分查找
将一个难以直接解决的大问题,分割成一些较小的同类问题,各个击破 。
二分查找又叫折半查找, 该方法主要将数列有序排列, 采用跳跃式的方式查找数据。
二分法查找的前提条件是被查找的数据必须是有序的。
分:原问题分解成若干子问题
治:对子问题分别求解
合:子问题的解合并成原问题的解
