2021-2022学年鲁教版(五四制)七年级数学上册《6.5一次函数的应用》选择题专项练习题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)七年级数学上册《6.5一次函数的应用》选择题专项练习题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 265.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-17 00:00:00 | ||
图片预览



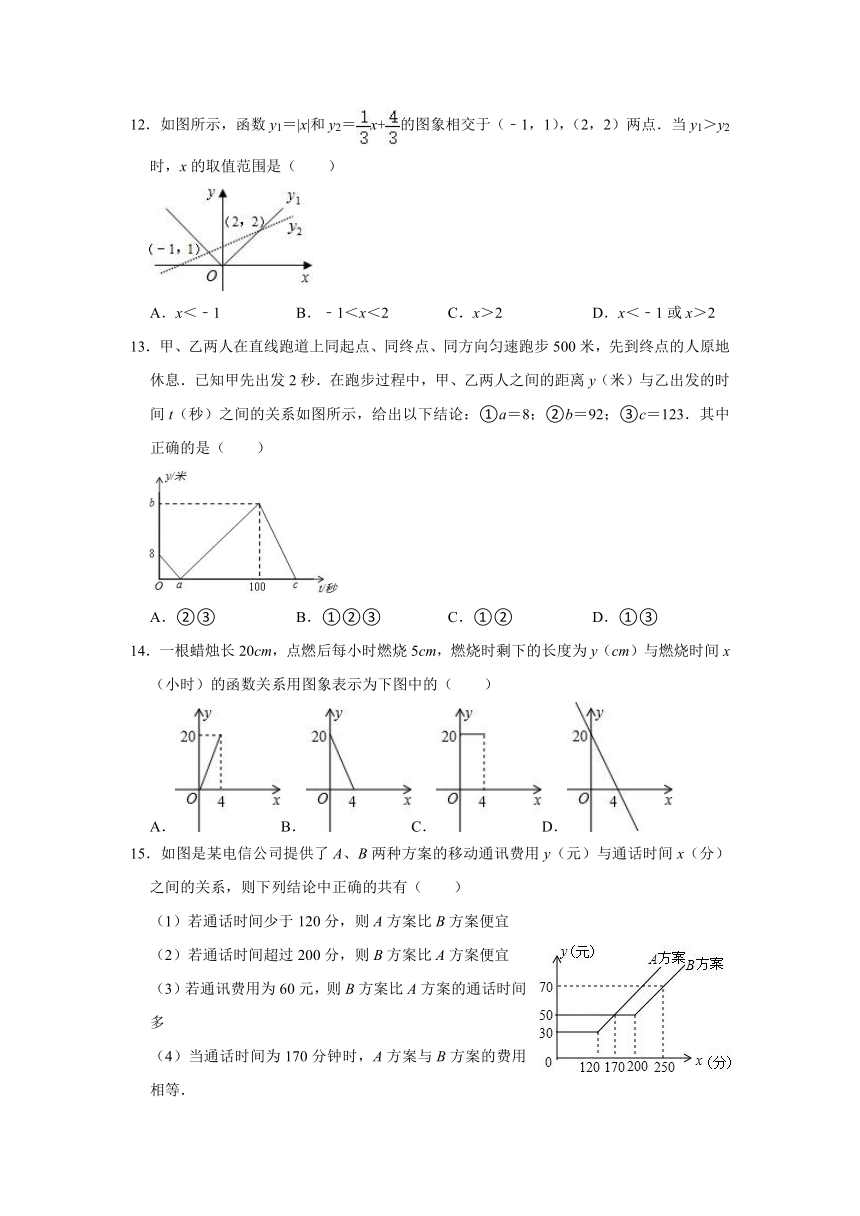
文档简介
2021-2022学年鲁教版七年级数学上册《6.5一次函数的应用》选择题专项练习题(附答案)
1.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
2.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时;
④乙先到达B地.
其中正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
A.0.5千米 B.1千米 C.1.5千米 D.2千米
4.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
A.x=0 B.x=﹣1 C.x=﹣2 D.x=1
5.弹簧的长度y(cm)与所挂物体的质量x(kg)关系如右图所示,当弹簧不挂重物时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
6.已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为( )
A.y=﹣x﹣2 B.y=﹣x﹣6 C.y=﹣x+10 D.y=﹣x﹣1
7.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是( )
A.x=2 B.x=4 C.x=8 D.x=10
8.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(,) B.(3,3) C.(,) D.(,)
9.在平面直角坐标系中,已知直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
10.如图,一次函数y=﹣2x+4的图象与坐标轴分别交于A、B两点,把线段AB绕着点A沿逆时针方向旋转90°,点B落在点B′处,则点B′的坐标是( )
A.(6,4) B.(4,6) C.(6,5) D.(5,6)
11.已知A,B两地相距400千米,章老师驾车以80千米/小时的速度从A地到B地.汽车出发前油箱中有油25升,途中加油若干升,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如下图所示.假设汽车每小时耗油量保持不变,以下说法错误的是( )
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达B地时油箱中还余油6升
12.如图所示,函数y1=|x|和y2=x+的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<﹣1 B.﹣1<x<2 C.x>2 D.x<﹣1或x>2
13.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.②③ B.①②③ C.①② D.①③
14.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度为y(cm)与燃烧时间x(小时)的函数关系用图象表示为下图中的( )
A.B.C.D.
15.如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有( )
(1)若通话时间少于120分,则A方案比B方案便宜
(2)若通话时间超过200分,则B方案比A方案便宜
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)当通话时间为170分钟时,A方案与B方案的费用相等.
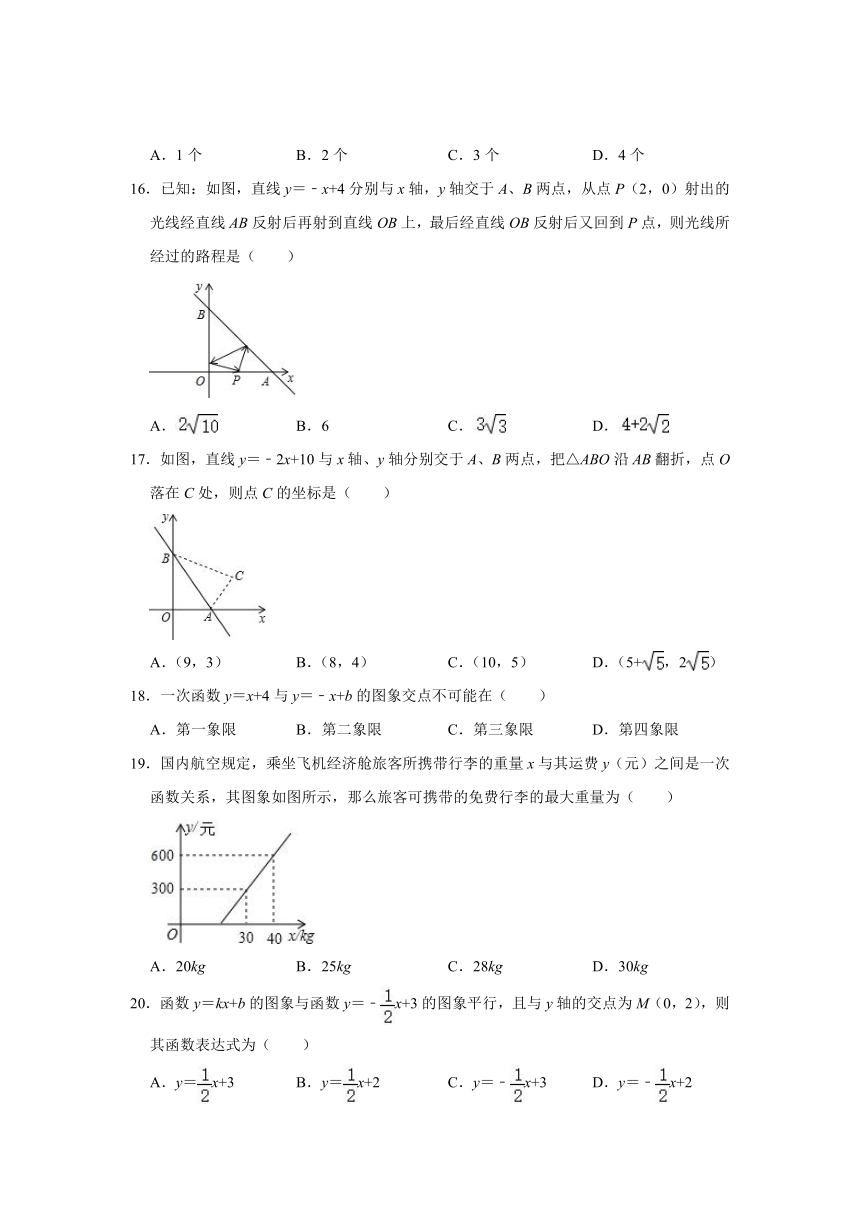
A.1个 B.2个 C.3个 D.4个
16.已知:如图,直线y=﹣x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A. B.6 C. D.
17.如图,直线y=﹣2x+10与x轴、y轴分别交于A、B两点,把△ABO沿AB翻折,点O落在C处,则点C的坐标是( )
A.(9,3) B.(8,4) C.(10,5) D.(5+,2)
18.一次函数y=x+4与y=﹣x+b的图象交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19.国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
A.20kg B.25kg C.28kg D.30kg
20.函数y=kx+b的图象与函数y=﹣x+3的图象平行,且与y轴的交点为M(0,2),则其函数表达式为( )
A.y=x+3 B.y=x+2 C.y=﹣x+3 D.y=﹣x+2
参考答案
1.解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选:B.
2.解:由函数图象可知,乙比甲晚出发1小时,故①正确;
乙出发3﹣1=2小时后追上甲,故②错误;
甲的速度为:12÷3=4(千米/小时),故③正确;
乙的速度为:12÷(3﹣1)=6(千米/小时),
则甲到达B地用的时间为:20÷4=5(小时),
乙到达B地用的时间为:20÷6=(小时),
1+3,
∴乙先到达B地,故④正确;
正确的有3个.
故选:C.
3.解:由甲的图象可知甲的速度为:12÷24=0.5千米/分,由乙的图象可知乙的速度为:12÷(18﹣6)=1千米/分,所以每分钟乙比甲多行驶的路程是0.5千米.
故选:A.
4.解:由函数图象,得两直线的交点坐标是(﹣1,﹣2),
k1x+b=k2x的解为x=﹣1,
故选:B.
5.解:设函数的解析式为y=kx+b,由函数图象,得
,
解得:,
∴y=x+10.
当x=0时,y=10.
故选:B.
6.解:设一次函数的解析式为y=kx+b.
由题意可得出方程组,
解得:,
那么此一次函数的解析式为:y=﹣x+10.
故选:C.
7.解:把(2,0)代入y=2x+b,
得:b=﹣4,把b=﹣4代入方程2x+b=0,
得:x=2.
故选:A.
8.解:过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
∠CMP=∠DNP=∠CPD=90°,
∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,
∵P(1,1),
∴OM=BN=1,PM=1,
在△MCP和△NPD中,
∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,
∵BD=2AD,
∴设AD=a,BD=2a,
∵P(1,1),
∴DN=2a﹣1,
则2a﹣1=1,
a=1,即BD=2.
∵直线y=x,
∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD==,
在Rt△MCP中,由勾股定理得:CM==2,
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,
把D(3,2)代入得:k=﹣,
即直线CD的解析式是y=﹣x+3,
即方程组得:,
即Q的坐标是(,).
故选:D.
9.解:过C作CD⊥AB于D,如图,
对于直线y=﹣x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3﹣n,
∴DA=OA=4,
∴DB=5﹣4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3﹣n)2,解得n=,
∴点C的坐标为(0,).
故选:B.
10.解:过B′点作B′E⊥x轴,于点E,作AD⊥B′E,
∵一次函数y=﹣2x+4的图象与坐标轴分别交于A、B两点,
∴y=0,即0=﹣2x+4,
∴x=2,
B点坐标为:(2,0),
∴A点坐标为:(0,4),
∵旋转前后图形全等,
∴AD=AO=4,B′D=BO=2,DE=AO=4,
∴B′E=6,
∴点B′的坐标是:(4,6).
故选:B.
11.解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.
将(0,25),(2,9)代入,得,
解得.
所以y=﹣8t+25,故A选项正确;
B、由图象可知,途中加油:30﹣9=21(升),故B选项正确;
C、由图可知汽车每小时用油(25﹣9)÷2=8(升),
所以汽车加油后还可行驶:30÷8=3<4(小时),故C选项错误;
D、∵汽车从甲地到达乙地,所需时间为:400÷80=5(小时),
∴5小时耗油量为:8×5=40(升),
又∵汽车出发前油箱有油25升,途中加油21升,
∴汽车到达乙地时油箱中还余油:25+21﹣40=6(升),故D选项正确.
故选:C.
12.解:当x≥0时,y1=x,又,
∵两直线的交点为(2,2),
∴当x<0时,y1=﹣x,又,
∵两直线的交点为(﹣1,1),
由图象可知:当y1>y2时x的取值范围为:x<﹣1或x>2.
故选:D.
13.解:甲的速度为:8÷2=4(米/秒);
乙的速度为:500÷100=5(米/秒);
b=5×100﹣4×(100+2)=92(米);
5a﹣4×(a+2)=0,
解得a=8,
c=100+92÷4=123(秒),
∴正确的有①②③.
故选:B.
14.解:蜡烛剩下的长度随时间增长而缩短,根据实际意义不可能是D,更不可能是A、C.
故选:B.
15.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
16.解:由题意知y=﹣x+4的点A(4,0),点B(0,4)
则点P(2,0)
设光线分别射在AB、OB上的M、N处,由于光线从点P经两次反射后又回到P点,
根据反射规律,则∠PMA=∠BMN;∠PNO=∠BNM.
作出点P关于OB的对称点P1,作出点P关于AB的对称点P2,则:
∠P2MA=∠PMA=∠BMN,∠P1NO=∠PNO=∠BNM,
∴P1,N,M,P2共线,
∵∠P2AB=∠PAB=45°,
即P2A⊥OA;
PM+MN+NP=P2M+MN+P1N=P1P2==2.
故选:A.
17.解:令y=﹣2x+10=0,
解得:x=5,
∴A点的坐标为:(5,0),
令x=0,得y=10,
∴B点的坐标为:(0,10)
∴OA=5,OB=10,
∴AB=5,
连接OC交AB于D点,作DE⊥x轴于E,作DF⊥y轴于F.
∴OD=×5×10÷(×5)=2,
∵OA2=AD AB
∴AD===.
∵△ADE∽△ABO
∴=
∴DE=OB=×10=2,
AE=OA=×5=1
则OE=4
∴点D的坐标是(4,2).
∵D是OC的中点.
∴点C的坐标是(8,4).
故选:B.
18.解:因为一次函数y=x+4的图象经过第一、二、三象限,不经过第四象限,
所以一次函数y=x+4与y=﹣x+b的图象交点不可能在第四象限.
故选:D.
19.解:设携带行李的重量x与其运费y(元)之间的函数关系式为y=kx+b,由题意,得
,
解得:,
∴y=30x﹣600.
当y=0时,30x﹣600=0,
∴x=20.
故选:A.
20.解:根据题意得:k=﹣
把(0,2)代入y=﹣x+b得:b=2
则函数的解析式是:y=﹣x+2
故选:D.
1.如图,已知点A(﹣1,0)和点B(1,2),在y轴上确定点P,使得△ABP为直角三角形,则满足条件的点P共有( )
A.5个 B.4个 C.3个 D.2个
2.A、B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:
①乙晚出发1小时;
②乙出发3小时后追上甲;
③甲的速度是4千米/小时;
④乙先到达B地.
其中正确的个数是( )
A.1 B.2 C.3 D.4
3.如图,表示甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶的路程是( )
A.0.5千米 B.1千米 C.1.5千米 D.2千米
4.同一平面直角坐标系中,一次函数y=k1x+b的图象与一次函数y=k2x的图象如图所示,则关于x的方程k1x+b=k2x的解为( )
A.x=0 B.x=﹣1 C.x=﹣2 D.x=1
5.弹簧的长度y(cm)与所挂物体的质量x(kg)关系如右图所示,当弹簧不挂重物时的长度是( )
A.9cm B.10cm C.10.5cm D.11cm
6.已知一次函数的图象与直线y=﹣x+1平行,且过点(8,2),那么此一次函数的解析式为( )
A.y=﹣x﹣2 B.y=﹣x﹣6 C.y=﹣x+10 D.y=﹣x﹣1
7.直线y=2x+b与x轴的交点坐标是(2,0),则关于x的方程2x+b=0的解是( )
A.x=2 B.x=4 C.x=8 D.x=10
8.如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=2AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为( )
A.(,) B.(3,3) C.(,) D.(,)
9.在平面直角坐标系中,已知直线y=﹣x+3与x轴、y轴分别交于A、B两点,点C(0,n)是y轴正半轴上一点.把坐标平面沿直线AC折叠,使点B刚好落在x轴上,则点C的坐标是( )
A.(0,) B.(0,) C.(0,3) D.(0,4)
10.如图,一次函数y=﹣2x+4的图象与坐标轴分别交于A、B两点,把线段AB绕着点A沿逆时针方向旋转90°,点B落在点B′处,则点B′的坐标是( )
A.(6,4) B.(4,6) C.(6,5) D.(5,6)
11.已知A,B两地相距400千米,章老师驾车以80千米/小时的速度从A地到B地.汽车出发前油箱中有油25升,途中加油若干升,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如下图所示.假设汽车每小时耗油量保持不变,以下说法错误的是( )
A.加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系是y=﹣8t+25
B.途中加油21升
C.汽车加油后还可行驶4小时
D.汽车到达B地时油箱中还余油6升
12.如图所示,函数y1=|x|和y2=x+的图象相交于(﹣1,1),(2,2)两点.当y1>y2时,x的取值范围是( )
A.x<﹣1 B.﹣1<x<2 C.x>2 D.x<﹣1或x>2
13.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.②③ B.①②③ C.①② D.①③
14.一根蜡烛长20cm,点燃后每小时燃烧5cm,燃烧时剩下的长度为y(cm)与燃烧时间x(小时)的函数关系用图象表示为下图中的( )
A.B.C.D.
15.如图是某电信公司提供了A、B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的共有( )
(1)若通话时间少于120分,则A方案比B方案便宜
(2)若通话时间超过200分,则B方案比A方案便宜
(3)若通讯费用为60元,则B方案比A方案的通话时间多
(4)当通话时间为170分钟时,A方案与B方案的费用相等.
A.1个 B.2个 C.3个 D.4个
16.已知:如图,直线y=﹣x+4分别与x轴,y轴交于A、B两点,从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )
A. B.6 C. D.
17.如图,直线y=﹣2x+10与x轴、y轴分别交于A、B两点,把△ABO沿AB翻折,点O落在C处,则点C的坐标是( )
A.(9,3) B.(8,4) C.(10,5) D.(5+,2)
18.一次函数y=x+4与y=﹣x+b的图象交点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
19.国内航空规定,乘坐飞机经济舱旅客所携带行李的重量x与其运费y(元)之间是一次函数关系,其图象如图所示,那么旅客可携带的免费行李的最大重量为( )
A.20kg B.25kg C.28kg D.30kg
20.函数y=kx+b的图象与函数y=﹣x+3的图象平行,且与y轴的交点为M(0,2),则其函数表达式为( )
A.y=x+3 B.y=x+2 C.y=﹣x+3 D.y=﹣x+2
参考答案
1.解:①以A为直角顶点,可过A作直线垂直于AB,与y轴交于一点,这一点符合点P的要求;
②以B为直角顶点,可过B作直线垂直于AB,与y轴交于一点,这一点也符合P点的要求;
③以P为直角顶点,与y轴共有2个交点.
所以满足条件的点P共有4个.
故选:B.
2.解:由函数图象可知,乙比甲晚出发1小时,故①正确;
乙出发3﹣1=2小时后追上甲,故②错误;
甲的速度为:12÷3=4(千米/小时),故③正确;
乙的速度为:12÷(3﹣1)=6(千米/小时),
则甲到达B地用的时间为:20÷4=5(小时),
乙到达B地用的时间为:20÷6=(小时),
1+3,
∴乙先到达B地,故④正确;
正确的有3个.
故选:C.
3.解:由甲的图象可知甲的速度为:12÷24=0.5千米/分,由乙的图象可知乙的速度为:12÷(18﹣6)=1千米/分,所以每分钟乙比甲多行驶的路程是0.5千米.
故选:A.
4.解:由函数图象,得两直线的交点坐标是(﹣1,﹣2),
k1x+b=k2x的解为x=﹣1,
故选:B.
5.解:设函数的解析式为y=kx+b,由函数图象,得
,
解得:,
∴y=x+10.
当x=0时,y=10.
故选:B.
6.解:设一次函数的解析式为y=kx+b.
由题意可得出方程组,
解得:,
那么此一次函数的解析式为:y=﹣x+10.
故选:C.
7.解:把(2,0)代入y=2x+b,
得:b=﹣4,把b=﹣4代入方程2x+b=0,
得:x=2.
故选:A.
8.解:过P作MN⊥y轴,交y轴于M,交AB于N,过D作DH⊥y轴,交y轴于H,
∠CMP=∠DNP=∠CPD=90°,
∴∠MCP+∠CPM=90°,∠MPC+∠DPN=90°,
∴∠MCP=∠DPN,
∵P(1,1),
∴OM=BN=1,PM=1,
在△MCP和△NPD中,
∴△MCP≌△NPD(AAS),
∴DN=PM,PN=CM,
∵BD=2AD,
∴设AD=a,BD=2a,
∵P(1,1),
∴DN=2a﹣1,
则2a﹣1=1,
a=1,即BD=2.
∵直线y=x,
∴AB=OB=3,
在Rt△DNP中,由勾股定理得:PC=PD==,
在Rt△MCP中,由勾股定理得:CM==2,
则C的坐标是(0,3),
设直线CD的解析式是y=kx+3,
把D(3,2)代入得:k=﹣,
即直线CD的解析式是y=﹣x+3,
即方程组得:,
即Q的坐标是(,).
故选:D.
9.解:过C作CD⊥AB于D,如图,
对于直线y=﹣x+3,
当x=0,得y=3;
当y=0,x=4,
∴A(4,0),B(0,3),即OA=4,OB=3,
∴AB=5,
又∵坐标平面沿直线AC折叠,使点B刚好落在x轴上,
∴AC平分∠OAB,
∴CD=CO=n,则BC=3﹣n,
∴DA=OA=4,
∴DB=5﹣4=1,
在Rt△BCD中,DC2+BD2=BC2,
∴n2+12=(3﹣n)2,解得n=,
∴点C的坐标为(0,).
故选:B.
10.解:过B′点作B′E⊥x轴,于点E,作AD⊥B′E,
∵一次函数y=﹣2x+4的图象与坐标轴分别交于A、B两点,
∴y=0,即0=﹣2x+4,
∴x=2,
B点坐标为:(2,0),
∴A点坐标为:(0,4),
∵旋转前后图形全等,
∴AD=AO=4,B′D=BO=2,DE=AO=4,
∴B′E=6,
∴点B′的坐标是:(4,6).
故选:B.
11.解:A、设加油前油箱中剩余油量y(升)与行驶时间t(小时)的函数关系式为y=kt+b.
将(0,25),(2,9)代入,得,
解得.
所以y=﹣8t+25,故A选项正确;
B、由图象可知,途中加油:30﹣9=21(升),故B选项正确;
C、由图可知汽车每小时用油(25﹣9)÷2=8(升),
所以汽车加油后还可行驶:30÷8=3<4(小时),故C选项错误;
D、∵汽车从甲地到达乙地,所需时间为:400÷80=5(小时),
∴5小时耗油量为:8×5=40(升),
又∵汽车出发前油箱有油25升,途中加油21升,
∴汽车到达乙地时油箱中还余油:25+21﹣40=6(升),故D选项正确.
故选:C.
12.解:当x≥0时,y1=x,又,
∵两直线的交点为(2,2),
∴当x<0时,y1=﹣x,又,
∵两直线的交点为(﹣1,1),
由图象可知:当y1>y2时x的取值范围为:x<﹣1或x>2.
故选:D.
13.解:甲的速度为:8÷2=4(米/秒);
乙的速度为:500÷100=5(米/秒);
b=5×100﹣4×(100+2)=92(米);
5a﹣4×(a+2)=0,
解得a=8,
c=100+92÷4=123(秒),
∴正确的有①②③.
故选:B.
14.解:蜡烛剩下的长度随时间增长而缩短,根据实际意义不可能是D,更不可能是A、C.
故选:B.
15.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当A方案与B方案的费用相等,通话时间为170分钟,故(4)正确;
故选:D.
16.解:由题意知y=﹣x+4的点A(4,0),点B(0,4)
则点P(2,0)
设光线分别射在AB、OB上的M、N处,由于光线从点P经两次反射后又回到P点,
根据反射规律,则∠PMA=∠BMN;∠PNO=∠BNM.
作出点P关于OB的对称点P1,作出点P关于AB的对称点P2,则:
∠P2MA=∠PMA=∠BMN,∠P1NO=∠PNO=∠BNM,
∴P1,N,M,P2共线,
∵∠P2AB=∠PAB=45°,
即P2A⊥OA;
PM+MN+NP=P2M+MN+P1N=P1P2==2.
故选:A.
17.解:令y=﹣2x+10=0,
解得:x=5,
∴A点的坐标为:(5,0),
令x=0,得y=10,
∴B点的坐标为:(0,10)
∴OA=5,OB=10,
∴AB=5,
连接OC交AB于D点,作DE⊥x轴于E,作DF⊥y轴于F.
∴OD=×5×10÷(×5)=2,
∵OA2=AD AB
∴AD===.
∵△ADE∽△ABO
∴=
∴DE=OB=×10=2,
AE=OA=×5=1
则OE=4
∴点D的坐标是(4,2).
∵D是OC的中点.
∴点C的坐标是(8,4).
故选:B.
18.解:因为一次函数y=x+4的图象经过第一、二、三象限,不经过第四象限,
所以一次函数y=x+4与y=﹣x+b的图象交点不可能在第四象限.
故选:D.
19.解:设携带行李的重量x与其运费y(元)之间的函数关系式为y=kx+b,由题意,得
,
解得:,
∴y=30x﹣600.
当y=0时,30x﹣600=0,
∴x=20.
故选:A.
20.解:根据题意得:k=﹣
把(0,2)代入y=﹣x+b得:b=2
则函数的解析式是:y=﹣x+2
故选:D.
