2021-2022学年苏科版八年级数学上册6.4用一次函数解决问题解答题专题提升训练(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学上册6.4用一次函数解决问题解答题专题提升训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 426.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 10:58:51 | ||
图片预览




文档简介
2021-2022学年苏科版八年级数学上册《6.4用一次函数解决问题》
解答题专题提升训练(附答案)
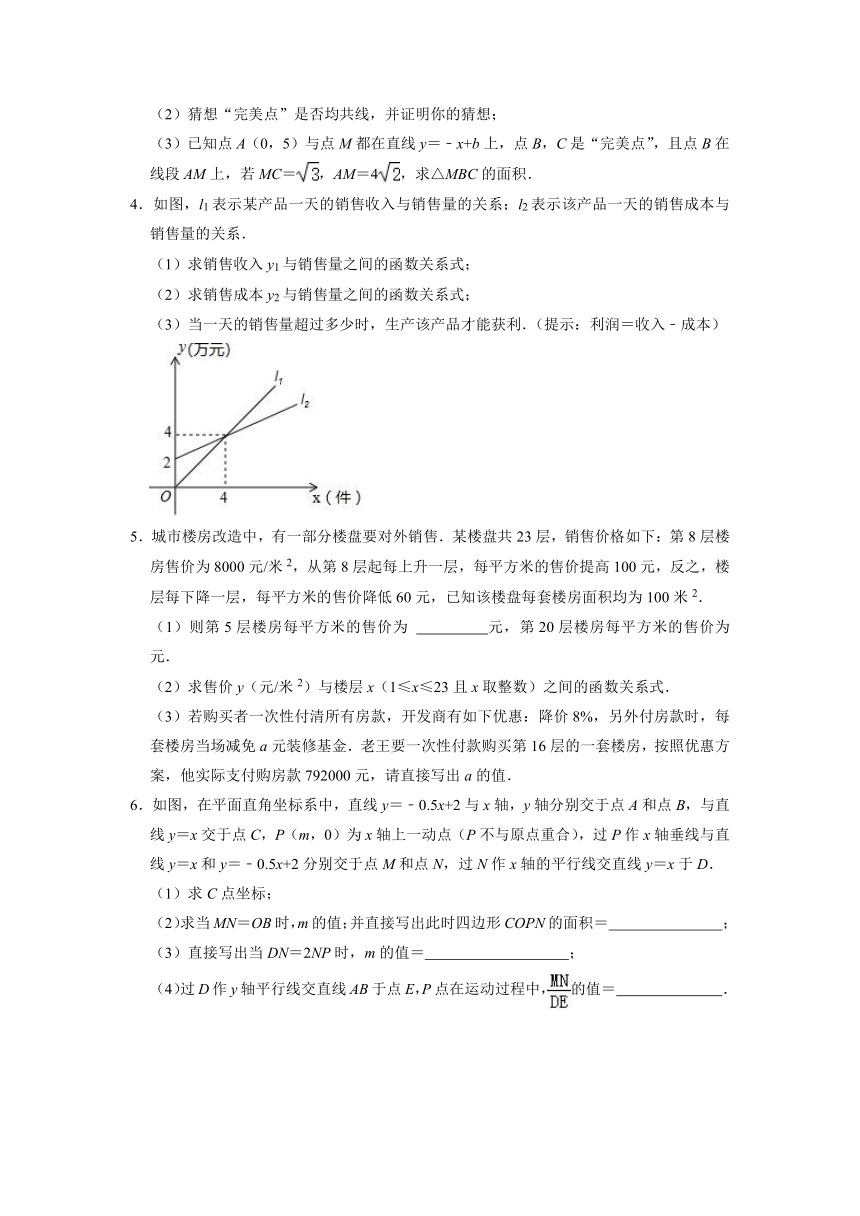
1.小明从家出发,外出散步,.到一个公共健身区活动了一会后,继续散步了一段时间到达了超市,然后回家,如图是小明在散步过程中离家的路程y(米)与离开家的时间x(米)之间的函数图象,根据图象信息解答下列问题.
(1)小明散步的速度为 米/分;
(2)若在小明出发2分钟时,小亮从小明家出发,沿小明散步的路线以48米/分的速度去超市.
①小亮去超市过程中y与x之间的函数关系式为 ;
②小亮去超市途中与小明相遇的时间为 .
2.甲、乙两人从学校出发,沿相同的线路跑向公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)图中b的值为 ;
(3)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(4)乙出发 秒后与甲第一次相遇.
3.当m,n是正实数,且满足m+n=mn时,就称点P(m,)为“完美点”.
(1)任意写出两组完美点;
(2)猜想“完美点”是否均共线,并证明你的猜想;
(3)已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=,AM=4,求△MBC的面积.
4.如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.
(1)求销售收入y1与销售量之间的函数关系式;
(2)求销售成本y2与销售量之间的函数关系式;
(3)当一天的销售量超过多少时,生产该产品才能获利.(提示:利润=收入﹣成本)
5.城市楼房改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第8层楼房售价为8000元/米2,从第8层起每上升一层,每平方米的售价提高100元,反之,楼层每下降一层,每平方米的售价降低60元,已知该楼盘每套楼房面积均为100米2.
(1)则第5层楼房每平方米的售价为 元,第20层楼房每平方米的售价为 元.
(2)求售价y(元/米2)与楼层x(1≤x≤23且x取整数)之间的函数关系式.
(3)若购买者一次性付清所有房款,开发商有如下优惠:降价8%,另外付房款时,每套楼房当场减免a元装修基金.老王要一次性付款购买第16层的一套楼房,按照优惠方案,他实际支付购房款792000元,请直接写出a的值.
6.如图,在平面直角坐标系中,直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,与直线y=x交于点C,P(m,0)为x轴上一动点(P不与原点重合),过P作x轴垂线与直线y=x和y=﹣0.5x+2分别交于点M和点N,过N作x轴的平行线交直线y=x于D.
(1)求C点坐标;
(2)求当MN=OB时,m的值;并直接写出此时四边形COPN的面积= ;
(3)直接写出当DN=2NP时,m的值= ;
(4)过D作y轴平行线交直线AB于点E,P点在运动过程中,的值= .
7.元旦某公司老板准备和员工去上海旅游,甲旅行社承诺,“老板一人免费,员工可享受八折优惠”;乙旅行社承诺:“包括老板在内所有人按全票的七五折优惠”,若全票价为2000元.
(1)设参加旅游的员工人数为x人,甲、乙旅行社收费分别为y甲(元)和y乙(元),直接写出两个旅行社收费的表达式;
(2)当员工有10人时,哪家旅行社更优惠?并说明理由.
8.甲、乙两人相约周末登阳台山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且当乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请根据图象所提供的信息解答下列问题:
(1)乙在A地时距地面的高度b为 米;t的值为 ;甲在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为 ;
(2)乙出发多长时间后,甲、乙两人第一次相遇?
9.甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地匀速开往乙地,轿车晚出发1h.货车和轿车各自与甲地的距离y(单位:km)与货车行驶的时间x(单位:小时)之间的关系如图所示.(1)求出图中的m和n的值;
(2)分别求出轿车行驶过程中y1,货车行驶过程中y2关于x的函数解析式,并写出自变量x的取值范围; (3)当轿车到达乙地时,求货车与乙地的距离.
10.甲骑电动车,乙骑自行车从同一出发地点沿同一路线到棋盘山游玩,设乙行驶的时间x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示,甲、乙两人之间的程差y关于x的函数图象如图②所示.请你解决以下问题:
(1)甲的速度是 km/h,乙的速度是 km/h;
(2)甲出发 h时,与乙相遇;
(3)对比图①、图②可知:a= ;
(4)乙出发 h时,甲、乙两人之间的路程差为7.5km.
11.如图,直线y=2x+1与x轴交于点A,与y轴交于点B.
(1)求A,B两点的坐标;
(2)将直线y=2x+1向下平移5个单位长度后的直线y2.
(3)过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.
12.某市为了鼓励居民节约用电,采用分段计费的方法按月计算用户的电费,每月用电量不超过210度时,按0.55元/度计费;每月用电量超过210度时,其中的210度仍按0.55元/度计费,超过的部分按0.6元/度计费,设用户每月用电量为x度,应交电费y元.
(1)求当x>210时,y与x的函数关系式;
(2)小林家12月份交纳电费145.5元,小林家这个月用电多少度?
13.某汽车在加油后开始匀速行驶.已知汽车行驶到20km时,油箱中剩油53L,行驶到50km时,油箱中剩油50L,如界油箱中剩余油量y(L)与汽车行驶路程x(km)之间是一次函数关系,请求出这个一次函数表达式,并写出自变量的取值范围.
14.《龟兔赛跑》是一则耐人寻味的寓言故事,故事中塑造了一只骄傲的兔子和一只坚持不懈的小乌龟.图中的线段OD和折线OABC表示“龟兔赛跑时时间与路程”的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 (填“兔子”或“乌龟”)的时间与路程的关系,赛跑的全过程是 米.
(2)乌龟用了多少分钟追上了正在睡觉的兔子?
(3)兔子醒来后,以300米/分钟的速度跑向终点,结果还是比乌龟晚到了1分钟,请问兔子在中间停下睡觉用了多少分钟?
15.如图,直线l:y=﹣x+3与x轴、y轴分别交于A、B两点,OM⊥AB于点M,点P为直线l上不与点A、B重合的一个动点.
(1)点A坐标为 ,点B坐标为 ,线段OM的长为 ;
(2)当△BOP的面积是6时,求点P的坐标;
(3)在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与△OMP全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.
16.我国是世界上严重缺水的国家之一,为了增强居民节约用水意识,某市准备实行新的水费收费标准:每户每月用水量不超过10吨的部分,按每吨3元收费,超过10吨的部分,按每吨5元收费,设某户月用水量为x吨,应交水费为y元.
(1)求出应交水费y(元)与用水量x(吨)(x>10)之间的函数关系式;
(2)已知居民甲上个月比居民乙多用4吨水,居民甲、乙共交水费100元,求他们上月分别用水多少吨?
17.周日,小慧从家沿着一条笔直的公路步行去新华书店看书,看了一段时间后,她按原路返回家中,小慧离家的距离y(单位:m)与她所用的时间t(单位:min)之间的函数关系如图所示,则小慧在新华书店看书的时间为多少?
18.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为w(元),求w与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第 天的日销售利润最大,最大日销售利润是 元(直接写出结果).
19.某天中午,小明从文具店步行返回学校,与此同时,小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计),然后原路返回学校,两人均匀速行驶,结果两人同时到达学校.小明、小亮两人离文具店的路程y1、y2(单位:米)与出发时间x(单位:分)之间的函数图象如图所示.
(1)学校和文具店之间的路程是 米,小亮的速度是小明速度的 倍;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)小明与小亮迎面相遇以后,再经过多长时间两人相距20米?
20.4月23日是“世界读书日“,某书店在这一天举行了购书优惠活动.方案一:享受当天购书标价8折的普通优惠;方案二:在普通优惠的基础上再打七五折,但需要缴纳50元权益卡费用.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两种方案,求y关于x的函数解析式;
(2)“世界读书日“这一天,如何选择哪种方案购书更省钱?
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
22.如图,一次函数y=kx+b的图象经过点A(0,5),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为2.
(1)求B点的坐标和k,b的值;
(2)证明直线y=kx+b与直线y=x互相垂直;
(3)在x轴上是否存在点P使△PAB为等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系中,过点C(0,6)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的函数表达式;
(2)在x轴上是否存在一点P,使PA+PC的值最小,若不存在,请说明理由,若存在,请求出点P的坐标;
(3)在x轴上是否存在点Q,使△AOQ是等腰三角形?如果存在,直接写出点Q的坐标;如果不存在,说明理由.
参考答案
1.解:(1)由图象可得,
小明散步的速度为:240÷3=80(米/分),
故答案为:80;
(2)①由图可得,小明家离超市400米,
400÷48=,
故小亮去超市过程中y与x之间的函数关系式为y=48x(0≤x≤),
故答案为:y=48x(0≤x≤);
②令48x=240,得x=5,
即小亮去超市途中与小明相遇的时间为5分钟,
故答案为:5分钟.
2.解:(1)由图象可得,
在跑步的全过程中,甲共跑了900米,甲的速度为:900÷600=1.5(米/秒),
故答案为:900,1.5;
(2)b=(1.5×500﹣150)÷1.5=400,
故答案为:400;
(3)由(2)知b=400,
则乙最早出发时跑步的速度为:(1.5×500)÷(400﹣100)=750÷300=2.5(米/秒),
乙在途中等候甲的时间为:500﹣400=100(秒),
故答案为:2.5,100;
(4)设乙出发m秒后与甲第一次相遇,
由题意可得2.5m=1.5(100+m),
解得m=150,
即乙出发150秒后与甲第一次相遇,
故答案为:150.
3.解:(1)把m=2代入m+n=mn得:2+n=2n,
解得:n=2,
即 ==1,
所以点(2,1)是“完美点”;
把m=3代入m+n=mn得:3+n=3n,
解得:n=,
即==2,
所以点(3,2)是“完美点”;
(2)“完美点”均共线,
证明:∵P(m,),m+n=mn且m,n是正实数,
∴除以n得:+1=m,即=m 1,
∴P(m,m﹣1),即“完美点”P在直线y=x﹣1上;
(3)∵点B,C是“完美点”,
∴直线BC的解析式为y=x﹣1,
∵点A(0,5)与点M都在直线y=﹣x+b上,
∴直线AM的解析式为:y=﹣x+5,
∵点B在线段AM上,
∴,
解得:,
∴B(3,2),
∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=﹣x,而直线y=x﹣1与直线y=x平行,直线y=﹣x+5与直线y=﹣x平行,
∴直线AM与直线y=x﹣1垂直,
∵点B是直线y=x﹣1与直线AM的交点,
∴垂足是点B,
∵点C是“完美点”,
∴点C在直线y=x﹣1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴AB=3,
∵AM=4,
∴BM=.
又∵CM=,
∴BC=1,
∴S△MBC=×BC×BM=×1×=.
4.解:(1)设销售收入y1与销售量x之间的函数关系式是y1=kx,
∵点(4,4)在该函数图象上,
∴4=4k,
解得k=1,
即销售收入y1与销售量x之间的函数关系式是y1=x;
(2)设销售成本y2与销售量x之间的函数关系式是y2=ax+b,
∵点(0,2),(4,4)在该函数图象上,
∴,
解得,
即销售成本y2与销售量x之间的函数关系式是y2=x+2;
(3)由图象可得,当x>4时,生产该产品才能获利.
5.解:(1)8000﹣60×(8﹣5)=8000﹣180=7820(元),
∴第5层楼房每平米的售价为7820元;
8000+100×(20﹣8)=8000+1200=9200(元),
∴第20层楼房每平米的售价为9200元;
故答案为:7820;9200;
(2)当1≤x≤8时,y=8000﹣(8﹣x)×60=60x+7520,
当9≤x≤23时,y=8000+(x﹣8)×100=100x+7200,
综上,售价y(元/米2)与楼层x(1≤x≤23且x取整数)之间的函数关系式为:y=60x+7520(1≤x≤8,且x取整数),y=100x+7200(9≤x≤23,且x取整数);
(3)当x=16时,
y=100×16+7200=8800,
∴8800×100×(1﹣8%)﹣a=792000,
解得:a=17600,
∴a的值为17600.
6.解:(1)∵点C是直线AB与直线OC的交点,
∴联立,
解得,
∴C(,).
(2)∵直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,
∴B(0,2),A(4,0),
∴OB=2,OA=4,
∵PN⊥x轴,
∴N(m,﹣0.5m+2),M(m,m),
∴MN=|m﹣(﹣0.5m+2)|=|1.5m﹣2|,
∵MN=OB,
∴|1.5m﹣2|=2,解得m=0(舍)或m=,
∴N(,),
∴PN=4﹣=,
∴四边形COPN的面积=S△OAC﹣S△APN=﹣=.
故答案为:.
(3)由(2)知,N(m,﹣0.5m+2),
∵DN∥x轴,且点D在直线y=x上,
∴D(﹣0.5m+2,﹣0.5m+2),
∴DN=|﹣0.5m+2﹣m|=|﹣1.5m+2|,
NP=|﹣0.5m+2|,
∵DN=2NP
∴|﹣1.5m+2|=2|﹣0.5m+2|,解得,m=﹣4或m=.
故答案为:﹣4或.
(4)如图,
由(2)和(3)可知,D(﹣0.5m+2,﹣0.5m+2),N(m,﹣0.5m+2),MN=|1.5m﹣2|,
∴E(﹣0.5m+2,0.25m+1),
∴DE=|0.25m+1﹣(﹣0.5m+2)|=|0.75m﹣1|=|1.5m﹣2|,
∴==2.
故答案为:2.
7.解:(1)由题意可得,
y甲=2000x×0.8=1600x,
y乙=2000(x+1)×0.75=1500x+1500,
即y甲=1600x,y乙=1500x+1500;
(2)当员工有10人时,甲旅行社更优惠,
理由:当x=10时,
y甲=1600×10=16000,
y乙=1500×10+1500=16500,
∵16000<16500,
∴当员工有10人时,甲旅行社更优惠.
8.解:(1)由图象可得,
乙开始登山速度为:15÷1=15(米/分钟),
则b=15×2=30,
甲的登上速度为:(300﹣100)÷20=200÷20=10(米/分钟),
则乙后来的登山速度为:10×3=30(米/分钟),
t=2+(300﹣30)÷30=2+270÷30=2+9=11,
设在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为y=kx+a,
∵点(0,100),(20,300)在该函数图象上,
∴,
解得,
即在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为y=20x+100,
故答案为:30,11,y=20x+100;
(2)设乙出发m分钟后,甲、乙两人第一次相遇,
100+10m=30+(m﹣2)×30,
解得m=6.5,
答:乙出发6.5分钟后,甲、乙两人第一次相遇.
9.解:(1)由图象可得,
货车的速度为:300÷5=60(km/h),
m=150÷60=2.5,
n=1+300÷[150÷(2.5﹣1)]=4,
即m的值是2.5,n的值是4;
(2)设轿车行驶过程中y1与x的函数关系式为y1=kx+b,
∵点(1,0),(2.5,150)在该函数图象上,
∴,
解得,
即轿车行驶过程中y1与x的函数关系式为y1=100x﹣100(1≤x≤4);
设货车行驶过程中y2关于x的函数解析式为y2=ax,
∵点(2.5,150)在该函数图象上,
∴2.5a=150,得a=60,
∴货车行驶过程中y2关于x的函数解析式为y2=60x(0≤x≤5);
(3)60×(5﹣4)
=60×1
=60(km),
即当轿车到达乙地时,货车与乙地的距离是60km.
10.解:(1)由图可得,
甲的速度为:25÷(1.5﹣0.5)=25÷1=25(km/h),
乙的速度为:25÷2.5=10(km/h),
故答案为:25,10;
(2)设甲出发mh后,甲、乙相遇,
由题可得,25m=10(m+0.5),解得m=,
故答案为:.
(3)由图可得,
a=25×(1.5﹣0.5)﹣10×1.5=10,
b=1.5,
故答案为:10;
(4)由题意可得,
前0.5h,乙行驶的路程为:10×0.5=5<7.5,
则甲、乙两人路程差为7.5km是在甲乙相遇之后,
设乙出发xh时,甲、乙两人路程差为7.5km,
25(x﹣0.5)﹣10x=7.5,
解得,x=,
25﹣10x=7.5,得x=;
即乙出h或h时,甲、乙两人路程差为7.5km.
故答案为:h或.
11.解:(1)当y=0时,2x+1=0,解得x=﹣,则A(﹣,0),
当x=0时,y=2x+1=1,则B(0,1);
(2)y=2x+1向下平移5个单位长度得到直线y2,则直线y2的表达式为:y2=2x+1﹣5=2x﹣4;
(3)设P(t,0),
∵OP=2OA,
∴|t|=2×=1,解得t=1或t=﹣1,
∴P点坐标为(1,0)或(﹣1,0),
设直线BP的解析式为y=kx+b,
把P(1,0),B(0,1)代入得,解得,此时直线BP的解析式为y=﹣x+1;
把P(﹣1,0),B(0,1)代入得,解得,此时直线BP的解析式为y=x+1;
综上所述,直线BP的解析式为y=﹣x+1或y=x+1.
12.解:(1)由题意可得,
当x>210时,y与x的函数关系式是y=0.55×210+(x﹣210)×0.6=0.6x﹣10.5,
即当x>210时,y与x的函数关系式是y=0.6x﹣10.5;
(2)∵当x=210时,应交电费210×0.55=115.5(元),115.5<145.5,
∴小林家12月份用电量超过210度,
令145.5=0.6x﹣10.5,
解得x=260,
答:小林家这个月用电260度.
13.解:设油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数解析式为y=kx+b,
由题意可得,
解得,
∴y=﹣0.1x+55,
当y=0时,0=﹣0.1x+55,得x=550,
即油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数解析式为y=﹣0.1x+55(0≤x≤550).
14.解:(1)由题意可得,
折线OABC表示赛跑过程中兔子的时间与路程的关系,
有函数图可得,赛跑的全过程是1350米,
故答案为:兔子,1350;
(2)由图象可得,
乌龟的速度为:1350÷45=30(米/分钟),
450÷30=15(分钟),
即乌龟用了15分钟追上了正在睡觉的兔子;
(3)兔子睡醒到跑到终点用的时间为:(1350﹣450)÷300=900÷300=3(分钟),
则兔子在中间停下睡觉用了(45+1﹣3)﹣3=43﹣3=40(分钟),
答:兔子在中间停下睡觉用了40分钟.
15.解:(1)对于直线y=﹣x+3,
令x=0,则y=3,令y=0,则﹣x+3=0,
解得:x=,
∴点A、B的坐标分别是(,0),(0,3),
∴OA=,OB=3,
∴AB===,
∵S△OAB=OA OB=AB OM,
∴OM==.
故答案为:(,0),(0,3),;
(2)如图,
设点P(x,﹣x+3),
∴S△BOP=OB x=×3x=6,
∴x=4,
∴点P的横坐标为4或﹣4,
∴横坐标为4时,﹣x+3=﹣,
∴横坐标为﹣4时,纵坐标为:﹣x+3=,
∴点P坐标为(4,﹣)或(﹣4,);
(3)存在,理由如下:
①当△OMP≌△PQO时,如图2和图3,
由(1)得OM=,
∴PQ=OM=,即P点横坐标为﹣或 ,
当P点横坐标为﹣时,纵坐标为:﹣+3=,
∴P(﹣,),
当P点横坐标为 时,纵坐标为:﹣+3=,
∴P( ),
此时点P的坐标为(﹣),( );
②当△OMP≌△OQP时,如图4和图5,
∴OQ=OM=,即点P、点Q纵坐标为﹣或 ,
由﹣x+3= ,解得:x=;
由﹣x+3=,解得:x=;
此时点P的坐标为( ),( );
综上所述,符合条件的点P的坐标为(﹣)或( )或( )或( );
16.解:(1)由题意,得:
当x>10时
y=3×10+5×(x﹣10),
即y=5x﹣20.
答:当x>10时,y(元)与x(吨)之间的函数关系式为y=5x﹣20;
(2)设甲上个月份用了a吨水,则乙上个月份用了(a﹣4)吨水,由题意,得:
5a﹣20+5(a﹣4)﹣20=100,
解得:a=16,
∴乙上个月用了16﹣4=12(吨水).
答:甲是16吨水,乙是12吨水.
17.解:设按原路返回家中的直线的解析式为:y=kx+b,
把(35,900),(50,0)代入可得:,
解得:,
返回时的解析式为y=﹣60x+3000,
当y=1200时,x=30,
由横坐标看出小慧在新华书店看书的时间用了30﹣15=15(min).
18.解:(1)当1≤x≤10时,设AB的解析式为:y=kx+b,
把A(1,300),B(10,120)代入得:
,
解得:,
∴AB:y=﹣20x+320(1≤x≤10),
当10<x≤30时,同理可得BC:y=14x﹣20,
综上所述,y与x之间的函数表达式为:y=;
(2)当1≤x≤10时,w=(10﹣6)(﹣20x+320)=﹣80x+1280,
当w=1040元,﹣80x+1280=1040,
解得:x=3,
∵﹣80<0,
∴w随x的增大而减小,
∴日销售利润不超过1040元的天数:3,4,5,6,7,8,9,10,一共8天;
当10<x≤30时,w=(10﹣6)(14x﹣20)=56x﹣80,
当w=1040元,56x﹣80=1040,
解得:x=20,
∵56>0,
∴w随x的增大而增大,
∴日销售利润不超过1040元的天数:11,12,13,14,15,16,17,18,19,20,一共10天;
综上所述,日销售利润不超过1040元的天数共有18天;
(3)当5≤x≤10时,当x=5时,w最大=﹣80×5+1280=880(元),
当10<x≤17时,当x=17时,w最大=56×17﹣80=872(元),
∴若5≤x≤17,第5天的日销售利润最大,最大日销售利润是880元,
故答案为:5,880.
19.解:(1)由图象可得,
学校和文具店之间的路程是360米,
∵小明从文具店步行返回学校,与此同时,小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计),然后原路返回学校,两人均匀速行驶,结果两人同时到达学校,
∴小亮的速度是小明速度的2倍,
故答案为:360,2;
(2)设小明的速度为m米/分钟,则小亮的速度为2m米/分钟,
2m+2×2m=360,
解得m=60,
∴a=2×60=120,
∴图中点M的横坐标、纵坐标的实际意义是两人出发2min后在距离文具店120m处相遇;
(3)设小明与小亮迎面相遇以后,再经过n分钟两人相距20米,
小亮未到达文具店时,(60+2×60)n=20,
解得n=;
小亮从文具店返回学校时,
60(2+n)﹣[(60×2)×(2+n)﹣360]=20,
解得n=;
由上可得,小明与小亮迎面相遇以后,再经过分钟或分钟两人相距20米.
20.解:(1)方案一应支付金额为:y=0.8x,
方案二应支付金额为:y=0.8x×0.75+50=0.6x+50;
答:方案一y关于x的函数解析式为:y=0.8x,方案二y关于x的函数解析式为:y=0.8x×0.75+50=0.6x+50;
(2)由0.8x=0.6x+50可得x=250,
∴当x<250时,选择方案一更省钱,
当x=250时,两种方案支付金额相同,
当x>250时,选择方案二更省钱.
21.解:(1)由题意可得,
计时制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.5x,
包月制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.2x+12;
(2)包月制收费方式比较合算,理由如下:
当x=60时,
计时制:每月应缴费用为:0.5×60=30(元),
包月制:每月应缴费用为:0.2×60+12=24(元),
∵30>24,
∴包月制收费方式比较合算;
(3)当y=100时,0.2x+12=100,
解得x=440.
答:该用户本月可通话440min.
22.解:(1)令x=2,则y=x=1,
∴B的坐标为(2,1),
将A,B两点坐标代入到直线y=kx+b中得,
,
解得,
∴B的坐标为(2,1),k=﹣2,b=5;
(2)证明:∵点A(0,5),B(2,1),
∴OA=5,OB==,AB==2,
∵52=()2+(22),
∴OA2=OB2+AB2,
∴∠ABO=90°,
∴直线y=kx+b与直线y=x互相垂直;
(3)∵△PAB为等腰三角形,
∴可以分三类讨论,
①当BA=BP时,如图,
此时P有两个位置,分别记为P和P′,
由(2)可得,AB=2,
∴PB=2,
设P(p,0),
∴PB==2,
解得:p=2+或p=2﹣,
∴P(2+,0)或P(2﹣,0);
②当AP=AB时,如图,
∵OA⊥x轴,OA=5,AB=2,
∴点A到x轴的距离为5,OA>AB,
∴此时在x轴上不存在点P使△PAB为等腰三角形;
③当PA=PB时,如图,
设P(m,0),
在Rt△POA中,PA2=OA2+OP2=52+m2=25+m2,
同理,PB2=12+(2﹣m)2=m2﹣4m+5,
∵PA=PB,
∴25+m2=m2﹣4m+5,
∴m=﹣5,
∴P(﹣5,0),
∴P(2+,0)或P(2﹣,0)或(﹣5,0).
23.解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AB的解析式是:y=﹣x+6;
(2)∵A(4,2),C(0,6),
作出点C关于x轴的对称点D(0,﹣6),
∴设直线AD的解析式为y=mx+n,
∴,
∴,
∴直线AD的解析式为y=2x﹣6,
令y=0,则2x﹣6=0,
∴x=3,
∴P(3,0);
(3)存在,理由:
设点Q(a,0),
∵点A(4,2),点O(0,0),
∴AO2=20,AQ2=(a﹣4)2+4,OQ2=a2,
①当AO=AQ时,
∴20=(a﹣4)2+4,
解得:a=8或0(舍去0);
②当AO=OQ时,
∴20=a2,
解得:a=;
③当AQ=OQ时,
∴(a﹣4)2+4=a2,
解得:a=;
故符合条件的点Q坐标为:(﹣2,0)或(2,0)或(8,0)或(,0).
解答题专题提升训练(附答案)
1.小明从家出发,外出散步,.到一个公共健身区活动了一会后,继续散步了一段时间到达了超市,然后回家,如图是小明在散步过程中离家的路程y(米)与离开家的时间x(米)之间的函数图象,根据图象信息解答下列问题.
(1)小明散步的速度为 米/分;
(2)若在小明出发2分钟时,小亮从小明家出发,沿小明散步的路线以48米/分的速度去超市.
①小亮去超市过程中y与x之间的函数关系式为 ;
②小亮去超市途中与小明相遇的时间为 .
2.甲、乙两人从学校出发,沿相同的线路跑向公园,甲先跑一段路程后,乙开始出发,当乙超过甲150米时,乙停在此地等候甲,两人相遇后,乙和甲一起以甲原来的速度继续跑向公园.如图是甲、乙两人在跑步的全过程中经过的路程y(米)与甲出发的时间x(秒)之间函数关系的图象,根据题意填空:
(1)在跑步的全过程中,甲共跑了 米,甲的速度为 米/秒;
(2)图中b的值为 ;
(3)乙最早出发时跑步的速度为 米/秒,乙在途中等候甲的时间为 秒;
(4)乙出发 秒后与甲第一次相遇.
3.当m,n是正实数,且满足m+n=mn时,就称点P(m,)为“完美点”.
(1)任意写出两组完美点;
(2)猜想“完美点”是否均共线,并证明你的猜想;
(3)已知点A(0,5)与点M都在直线y=﹣x+b上,点B,C是“完美点”,且点B在线段AM上,若MC=,AM=4,求△MBC的面积.
4.如图,l1表示某产品一天的销售收入与销售量的关系;l2表示该产品一天的销售成本与销售量的关系.
(1)求销售收入y1与销售量之间的函数关系式;
(2)求销售成本y2与销售量之间的函数关系式;
(3)当一天的销售量超过多少时,生产该产品才能获利.(提示:利润=收入﹣成本)
5.城市楼房改造中,有一部分楼盘要对外销售.某楼盘共23层,销售价格如下:第8层楼房售价为8000元/米2,从第8层起每上升一层,每平方米的售价提高100元,反之,楼层每下降一层,每平方米的售价降低60元,已知该楼盘每套楼房面积均为100米2.
(1)则第5层楼房每平方米的售价为 元,第20层楼房每平方米的售价为 元.
(2)求售价y(元/米2)与楼层x(1≤x≤23且x取整数)之间的函数关系式.
(3)若购买者一次性付清所有房款,开发商有如下优惠:降价8%,另外付房款时,每套楼房当场减免a元装修基金.老王要一次性付款购买第16层的一套楼房,按照优惠方案,他实际支付购房款792000元,请直接写出a的值.
6.如图,在平面直角坐标系中,直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,与直线y=x交于点C,P(m,0)为x轴上一动点(P不与原点重合),过P作x轴垂线与直线y=x和y=﹣0.5x+2分别交于点M和点N,过N作x轴的平行线交直线y=x于D.
(1)求C点坐标;
(2)求当MN=OB时,m的值;并直接写出此时四边形COPN的面积= ;
(3)直接写出当DN=2NP时,m的值= ;
(4)过D作y轴平行线交直线AB于点E,P点在运动过程中,的值= .
7.元旦某公司老板准备和员工去上海旅游,甲旅行社承诺,“老板一人免费,员工可享受八折优惠”;乙旅行社承诺:“包括老板在内所有人按全票的七五折优惠”,若全票价为2000元.
(1)设参加旅游的员工人数为x人,甲、乙旅行社收费分别为y甲(元)和y乙(元),直接写出两个旅行社收费的表达式;
(2)当员工有10人时,哪家旅行社更优惠?并说明理由.
8.甲、乙两人相约周末登阳台山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,且当乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请根据图象所提供的信息解答下列问题:
(1)乙在A地时距地面的高度b为 米;t的值为 ;甲在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为 ;
(2)乙出发多长时间后,甲、乙两人第一次相遇?
9.甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地匀速开往乙地,轿车晚出发1h.货车和轿车各自与甲地的距离y(单位:km)与货车行驶的时间x(单位:小时)之间的关系如图所示.(1)求出图中的m和n的值;
(2)分别求出轿车行驶过程中y1,货车行驶过程中y2关于x的函数解析式,并写出自变量x的取值范围; (3)当轿车到达乙地时,求货车与乙地的距离.
10.甲骑电动车,乙骑自行车从同一出发地点沿同一路线到棋盘山游玩,设乙行驶的时间x(h),甲、乙两人距出发点的路程S甲、S乙关于x的函数图象如图①所示,甲、乙两人之间的程差y关于x的函数图象如图②所示.请你解决以下问题:
(1)甲的速度是 km/h,乙的速度是 km/h;
(2)甲出发 h时,与乙相遇;
(3)对比图①、图②可知:a= ;
(4)乙出发 h时,甲、乙两人之间的路程差为7.5km.
11.如图,直线y=2x+1与x轴交于点A,与y轴交于点B.
(1)求A,B两点的坐标;
(2)将直线y=2x+1向下平移5个单位长度后的直线y2.
(3)过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.
12.某市为了鼓励居民节约用电,采用分段计费的方法按月计算用户的电费,每月用电量不超过210度时,按0.55元/度计费;每月用电量超过210度时,其中的210度仍按0.55元/度计费,超过的部分按0.6元/度计费,设用户每月用电量为x度,应交电费y元.
(1)求当x>210时,y与x的函数关系式;
(2)小林家12月份交纳电费145.5元,小林家这个月用电多少度?
13.某汽车在加油后开始匀速行驶.已知汽车行驶到20km时,油箱中剩油53L,行驶到50km时,油箱中剩油50L,如界油箱中剩余油量y(L)与汽车行驶路程x(km)之间是一次函数关系,请求出这个一次函数表达式,并写出自变量的取值范围.
14.《龟兔赛跑》是一则耐人寻味的寓言故事,故事中塑造了一只骄傲的兔子和一只坚持不懈的小乌龟.图中的线段OD和折线OABC表示“龟兔赛跑时时间与路程”的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中 (填“兔子”或“乌龟”)的时间与路程的关系,赛跑的全过程是 米.
(2)乌龟用了多少分钟追上了正在睡觉的兔子?
(3)兔子醒来后,以300米/分钟的速度跑向终点,结果还是比乌龟晚到了1分钟,请问兔子在中间停下睡觉用了多少分钟?
15.如图,直线l:y=﹣x+3与x轴、y轴分别交于A、B两点,OM⊥AB于点M,点P为直线l上不与点A、B重合的一个动点.
(1)点A坐标为 ,点B坐标为 ,线段OM的长为 ;
(2)当△BOP的面积是6时,求点P的坐标;
(3)在y轴上是否存在点Q,使得以O、P、Q为顶点的三角形与△OMP全等,若存在,请直接写出所有符合条件的点P的坐标,否则,说明理由.
16.我国是世界上严重缺水的国家之一,为了增强居民节约用水意识,某市准备实行新的水费收费标准:每户每月用水量不超过10吨的部分,按每吨3元收费,超过10吨的部分,按每吨5元收费,设某户月用水量为x吨,应交水费为y元.
(1)求出应交水费y(元)与用水量x(吨)(x>10)之间的函数关系式;
(2)已知居民甲上个月比居民乙多用4吨水,居民甲、乙共交水费100元,求他们上月分别用水多少吨?
17.周日,小慧从家沿着一条笔直的公路步行去新华书店看书,看了一段时间后,她按原路返回家中,小慧离家的距离y(单位:m)与她所用的时间t(单位:min)之间的函数关系如图所示,则小慧在新华书店看书的时间为多少?
18.某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试销售,售价为10元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘制成图象,图中的折线ABC表示日销售量y(件)与销售时间x(天)之间的函数关系.
(1)求y与x之间的函数表达式,并写出x的取值范围;
(2)若该节能产品的日销售利润为w(元),求w与x之间的函数表达式,并求出日销售利润不超过1040元的天数共有多少天?
(3)若5≤x≤17,直接写出第 天的日销售利润最大,最大日销售利润是 元(直接写出结果).
19.某天中午,小明从文具店步行返回学校,与此同时,小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计),然后原路返回学校,两人均匀速行驶,结果两人同时到达学校.小明、小亮两人离文具店的路程y1、y2(单位:米)与出发时间x(单位:分)之间的函数图象如图所示.
(1)学校和文具店之间的路程是 米,小亮的速度是小明速度的 倍;
(2)求a的值,并解释图中点M的横坐标、纵坐标的实际意义;
(3)小明与小亮迎面相遇以后,再经过多长时间两人相距20米?
20.4月23日是“世界读书日“,某书店在这一天举行了购书优惠活动.方案一:享受当天购书标价8折的普通优惠;方案二:在普通优惠的基础上再打七五折,但需要缴纳50元权益卡费用.
(1)以x(单位:元)表示标价总额,y(单位:元)表示应支付金额,分别就两种方案,求y关于x的函数解析式;
(2)“世界读书日“这一天,如何选择哪种方案购书更省钱?
21.某电信公司手机通讯有两种收费方式:(A)计时制:0.5元/min;(B)包月制:月租12元,另外通话费按0.2元/min.
(1)写出两种方式每月应缴费用y(元)与通话时间x(min)之间的关系式.
(2)某手机用户平均每个月通话时间为60min,他采用哪种方式较合算?为什么?
(3)如果该用户本月预缴了100元的话费,按包月制算,该用户本月可通话多长时间?
22.如图,一次函数y=kx+b的图象经过点A(0,5),并与直线y=x相交于点B,与x轴相交于点C,其中点B的横坐标为2.
(1)求B点的坐标和k,b的值;
(2)证明直线y=kx+b与直线y=x互相垂直;
(3)在x轴上是否存在点P使△PAB为等腰三角形?若存在,请直接写出点P坐标;若不存在,请说明理由.
23.如图,在平面直角坐标系中,过点C(0,6)的直线AB与直线OA相交于点A(4,2).
(1)求直线AB的函数表达式;
(2)在x轴上是否存在一点P,使PA+PC的值最小,若不存在,请说明理由,若存在,请求出点P的坐标;
(3)在x轴上是否存在点Q,使△AOQ是等腰三角形?如果存在,直接写出点Q的坐标;如果不存在,说明理由.
参考答案
1.解:(1)由图象可得,
小明散步的速度为:240÷3=80(米/分),
故答案为:80;
(2)①由图可得,小明家离超市400米,
400÷48=,
故小亮去超市过程中y与x之间的函数关系式为y=48x(0≤x≤),
故答案为:y=48x(0≤x≤);
②令48x=240,得x=5,
即小亮去超市途中与小明相遇的时间为5分钟,
故答案为:5分钟.
2.解:(1)由图象可得,
在跑步的全过程中,甲共跑了900米,甲的速度为:900÷600=1.5(米/秒),
故答案为:900,1.5;
(2)b=(1.5×500﹣150)÷1.5=400,
故答案为:400;
(3)由(2)知b=400,
则乙最早出发时跑步的速度为:(1.5×500)÷(400﹣100)=750÷300=2.5(米/秒),
乙在途中等候甲的时间为:500﹣400=100(秒),
故答案为:2.5,100;
(4)设乙出发m秒后与甲第一次相遇,
由题意可得2.5m=1.5(100+m),
解得m=150,
即乙出发150秒后与甲第一次相遇,
故答案为:150.
3.解:(1)把m=2代入m+n=mn得:2+n=2n,
解得:n=2,
即 ==1,
所以点(2,1)是“完美点”;
把m=3代入m+n=mn得:3+n=3n,
解得:n=,
即==2,
所以点(3,2)是“完美点”;
(2)“完美点”均共线,
证明:∵P(m,),m+n=mn且m,n是正实数,
∴除以n得:+1=m,即=m 1,
∴P(m,m﹣1),即“完美点”P在直线y=x﹣1上;
(3)∵点B,C是“完美点”,
∴直线BC的解析式为y=x﹣1,
∵点A(0,5)与点M都在直线y=﹣x+b上,
∴直线AM的解析式为:y=﹣x+5,
∵点B在线段AM上,
∴,
解得:,
∴B(3,2),
∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=﹣x,而直线y=x﹣1与直线y=x平行,直线y=﹣x+5与直线y=﹣x平行,
∴直线AM与直线y=x﹣1垂直,
∵点B是直线y=x﹣1与直线AM的交点,
∴垂足是点B,
∵点C是“完美点”,
∴点C在直线y=x﹣1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴AB=3,
∵AM=4,
∴BM=.
又∵CM=,
∴BC=1,
∴S△MBC=×BC×BM=×1×=.
4.解:(1)设销售收入y1与销售量x之间的函数关系式是y1=kx,
∵点(4,4)在该函数图象上,
∴4=4k,
解得k=1,
即销售收入y1与销售量x之间的函数关系式是y1=x;
(2)设销售成本y2与销售量x之间的函数关系式是y2=ax+b,
∵点(0,2),(4,4)在该函数图象上,
∴,
解得,
即销售成本y2与销售量x之间的函数关系式是y2=x+2;
(3)由图象可得,当x>4时,生产该产品才能获利.
5.解:(1)8000﹣60×(8﹣5)=8000﹣180=7820(元),
∴第5层楼房每平米的售价为7820元;
8000+100×(20﹣8)=8000+1200=9200(元),
∴第20层楼房每平米的售价为9200元;
故答案为:7820;9200;
(2)当1≤x≤8时,y=8000﹣(8﹣x)×60=60x+7520,
当9≤x≤23时,y=8000+(x﹣8)×100=100x+7200,
综上,售价y(元/米2)与楼层x(1≤x≤23且x取整数)之间的函数关系式为:y=60x+7520(1≤x≤8,且x取整数),y=100x+7200(9≤x≤23,且x取整数);
(3)当x=16时,
y=100×16+7200=8800,
∴8800×100×(1﹣8%)﹣a=792000,
解得:a=17600,
∴a的值为17600.
6.解:(1)∵点C是直线AB与直线OC的交点,
∴联立,
解得,
∴C(,).
(2)∵直线y=﹣0.5x+2与x轴,y轴分别交于点A和点B,
∴B(0,2),A(4,0),
∴OB=2,OA=4,
∵PN⊥x轴,
∴N(m,﹣0.5m+2),M(m,m),
∴MN=|m﹣(﹣0.5m+2)|=|1.5m﹣2|,
∵MN=OB,
∴|1.5m﹣2|=2,解得m=0(舍)或m=,
∴N(,),
∴PN=4﹣=,
∴四边形COPN的面积=S△OAC﹣S△APN=﹣=.
故答案为:.
(3)由(2)知,N(m,﹣0.5m+2),
∵DN∥x轴,且点D在直线y=x上,
∴D(﹣0.5m+2,﹣0.5m+2),
∴DN=|﹣0.5m+2﹣m|=|﹣1.5m+2|,
NP=|﹣0.5m+2|,
∵DN=2NP
∴|﹣1.5m+2|=2|﹣0.5m+2|,解得,m=﹣4或m=.
故答案为:﹣4或.
(4)如图,
由(2)和(3)可知,D(﹣0.5m+2,﹣0.5m+2),N(m,﹣0.5m+2),MN=|1.5m﹣2|,
∴E(﹣0.5m+2,0.25m+1),
∴DE=|0.25m+1﹣(﹣0.5m+2)|=|0.75m﹣1|=|1.5m﹣2|,
∴==2.
故答案为:2.
7.解:(1)由题意可得,
y甲=2000x×0.8=1600x,
y乙=2000(x+1)×0.75=1500x+1500,
即y甲=1600x,y乙=1500x+1500;
(2)当员工有10人时,甲旅行社更优惠,
理由:当x=10时,
y甲=1600×10=16000,
y乙=1500×10+1500=16500,
∵16000<16500,
∴当员工有10人时,甲旅行社更优惠.
8.解:(1)由图象可得,
乙开始登山速度为:15÷1=15(米/分钟),
则b=15×2=30,
甲的登上速度为:(300﹣100)÷20=200÷20=10(米/分钟),
则乙后来的登山速度为:10×3=30(米/分钟),
t=2+(300﹣30)÷30=2+270÷30=2+9=11,
设在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为y=kx+a,
∵点(0,100),(20,300)在该函数图象上,
∴,
解得,
即在登山全程中,距离地面高度y(米)与登山时间x(分)之间的函数关系式为y=20x+100,
故答案为:30,11,y=20x+100;
(2)设乙出发m分钟后,甲、乙两人第一次相遇,
100+10m=30+(m﹣2)×30,
解得m=6.5,
答:乙出发6.5分钟后,甲、乙两人第一次相遇.
9.解:(1)由图象可得,
货车的速度为:300÷5=60(km/h),
m=150÷60=2.5,
n=1+300÷[150÷(2.5﹣1)]=4,
即m的值是2.5,n的值是4;
(2)设轿车行驶过程中y1与x的函数关系式为y1=kx+b,
∵点(1,0),(2.5,150)在该函数图象上,
∴,
解得,
即轿车行驶过程中y1与x的函数关系式为y1=100x﹣100(1≤x≤4);
设货车行驶过程中y2关于x的函数解析式为y2=ax,
∵点(2.5,150)在该函数图象上,
∴2.5a=150,得a=60,
∴货车行驶过程中y2关于x的函数解析式为y2=60x(0≤x≤5);
(3)60×(5﹣4)
=60×1
=60(km),
即当轿车到达乙地时,货车与乙地的距离是60km.
10.解:(1)由图可得,
甲的速度为:25÷(1.5﹣0.5)=25÷1=25(km/h),
乙的速度为:25÷2.5=10(km/h),
故答案为:25,10;
(2)设甲出发mh后,甲、乙相遇,
由题可得,25m=10(m+0.5),解得m=,
故答案为:.
(3)由图可得,
a=25×(1.5﹣0.5)﹣10×1.5=10,
b=1.5,
故答案为:10;
(4)由题意可得,
前0.5h,乙行驶的路程为:10×0.5=5<7.5,
则甲、乙两人路程差为7.5km是在甲乙相遇之后,
设乙出发xh时,甲、乙两人路程差为7.5km,
25(x﹣0.5)﹣10x=7.5,
解得,x=,
25﹣10x=7.5,得x=;
即乙出h或h时,甲、乙两人路程差为7.5km.
故答案为:h或.
11.解:(1)当y=0时,2x+1=0,解得x=﹣,则A(﹣,0),
当x=0时,y=2x+1=1,则B(0,1);
(2)y=2x+1向下平移5个单位长度得到直线y2,则直线y2的表达式为:y2=2x+1﹣5=2x﹣4;
(3)设P(t,0),
∵OP=2OA,
∴|t|=2×=1,解得t=1或t=﹣1,
∴P点坐标为(1,0)或(﹣1,0),
设直线BP的解析式为y=kx+b,
把P(1,0),B(0,1)代入得,解得,此时直线BP的解析式为y=﹣x+1;
把P(﹣1,0),B(0,1)代入得,解得,此时直线BP的解析式为y=x+1;
综上所述,直线BP的解析式为y=﹣x+1或y=x+1.
12.解:(1)由题意可得,
当x>210时,y与x的函数关系式是y=0.55×210+(x﹣210)×0.6=0.6x﹣10.5,
即当x>210时,y与x的函数关系式是y=0.6x﹣10.5;
(2)∵当x=210时,应交电费210×0.55=115.5(元),115.5<145.5,
∴小林家12月份用电量超过210度,
令145.5=0.6x﹣10.5,
解得x=260,
答:小林家这个月用电260度.
13.解:设油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数解析式为y=kx+b,
由题意可得,
解得,
∴y=﹣0.1x+55,
当y=0时,0=﹣0.1x+55,得x=550,
即油箱中剩余油量y(L)与汽车行驶路程x(km)之间的函数解析式为y=﹣0.1x+55(0≤x≤550).
14.解:(1)由题意可得,
折线OABC表示赛跑过程中兔子的时间与路程的关系,
有函数图可得,赛跑的全过程是1350米,
故答案为:兔子,1350;
(2)由图象可得,
乌龟的速度为:1350÷45=30(米/分钟),
450÷30=15(分钟),
即乌龟用了15分钟追上了正在睡觉的兔子;
(3)兔子睡醒到跑到终点用的时间为:(1350﹣450)÷300=900÷300=3(分钟),
则兔子在中间停下睡觉用了(45+1﹣3)﹣3=43﹣3=40(分钟),
答:兔子在中间停下睡觉用了40分钟.
15.解:(1)对于直线y=﹣x+3,
令x=0,则y=3,令y=0,则﹣x+3=0,
解得:x=,
∴点A、B的坐标分别是(,0),(0,3),
∴OA=,OB=3,
∴AB===,
∵S△OAB=OA OB=AB OM,
∴OM==.
故答案为:(,0),(0,3),;
(2)如图,
设点P(x,﹣x+3),
∴S△BOP=OB x=×3x=6,
∴x=4,
∴点P的横坐标为4或﹣4,
∴横坐标为4时,﹣x+3=﹣,
∴横坐标为﹣4时,纵坐标为:﹣x+3=,
∴点P坐标为(4,﹣)或(﹣4,);
(3)存在,理由如下:
①当△OMP≌△PQO时,如图2和图3,
由(1)得OM=,
∴PQ=OM=,即P点横坐标为﹣或 ,
当P点横坐标为﹣时,纵坐标为:﹣+3=,
∴P(﹣,),
当P点横坐标为 时,纵坐标为:﹣+3=,
∴P( ),
此时点P的坐标为(﹣),( );
②当△OMP≌△OQP时,如图4和图5,
∴OQ=OM=,即点P、点Q纵坐标为﹣或 ,
由﹣x+3= ,解得:x=;
由﹣x+3=,解得:x=;
此时点P的坐标为( ),( );
综上所述,符合条件的点P的坐标为(﹣)或( )或( )或( );
16.解:(1)由题意,得:
当x>10时
y=3×10+5×(x﹣10),
即y=5x﹣20.
答:当x>10时,y(元)与x(吨)之间的函数关系式为y=5x﹣20;
(2)设甲上个月份用了a吨水,则乙上个月份用了(a﹣4)吨水,由题意,得:
5a﹣20+5(a﹣4)﹣20=100,
解得:a=16,
∴乙上个月用了16﹣4=12(吨水).
答:甲是16吨水,乙是12吨水.
17.解:设按原路返回家中的直线的解析式为:y=kx+b,
把(35,900),(50,0)代入可得:,
解得:,
返回时的解析式为y=﹣60x+3000,
当y=1200时,x=30,
由横坐标看出小慧在新华书店看书的时间用了30﹣15=15(min).
18.解:(1)当1≤x≤10时,设AB的解析式为:y=kx+b,
把A(1,300),B(10,120)代入得:
,
解得:,
∴AB:y=﹣20x+320(1≤x≤10),
当10<x≤30时,同理可得BC:y=14x﹣20,
综上所述,y与x之间的函数表达式为:y=;
(2)当1≤x≤10时,w=(10﹣6)(﹣20x+320)=﹣80x+1280,
当w=1040元,﹣80x+1280=1040,
解得:x=3,
∵﹣80<0,
∴w随x的增大而减小,
∴日销售利润不超过1040元的天数:3,4,5,6,7,8,9,10,一共8天;
当10<x≤30时,w=(10﹣6)(14x﹣20)=56x﹣80,
当w=1040元,56x﹣80=1040,
解得:x=20,
∵56>0,
∴w随x的增大而增大,
∴日销售利润不超过1040元的天数:11,12,13,14,15,16,17,18,19,20,一共10天;
综上所述,日销售利润不超过1040元的天数共有18天;
(3)当5≤x≤10时,当x=5时,w最大=﹣80×5+1280=880(元),
当10<x≤17时,当x=17时,w最大=56×17﹣80=872(元),
∴若5≤x≤17,第5天的日销售利润最大,最大日销售利润是880元,
故答案为:5,880.
19.解:(1)由图象可得,
学校和文具店之间的路程是360米,
∵小明从文具店步行返回学校,与此同时,小亮从学校骑自行车去文具店购买文具(购买文具时间忽略不计),然后原路返回学校,两人均匀速行驶,结果两人同时到达学校,
∴小亮的速度是小明速度的2倍,
故答案为:360,2;
(2)设小明的速度为m米/分钟,则小亮的速度为2m米/分钟,
2m+2×2m=360,
解得m=60,
∴a=2×60=120,
∴图中点M的横坐标、纵坐标的实际意义是两人出发2min后在距离文具店120m处相遇;
(3)设小明与小亮迎面相遇以后,再经过n分钟两人相距20米,
小亮未到达文具店时,(60+2×60)n=20,
解得n=;
小亮从文具店返回学校时,
60(2+n)﹣[(60×2)×(2+n)﹣360]=20,
解得n=;
由上可得,小明与小亮迎面相遇以后,再经过分钟或分钟两人相距20米.
20.解:(1)方案一应支付金额为:y=0.8x,
方案二应支付金额为:y=0.8x×0.75+50=0.6x+50;
答:方案一y关于x的函数解析式为:y=0.8x,方案二y关于x的函数解析式为:y=0.8x×0.75+50=0.6x+50;
(2)由0.8x=0.6x+50可得x=250,
∴当x<250时,选择方案一更省钱,
当x=250时,两种方案支付金额相同,
当x>250时,选择方案二更省钱.
21.解:(1)由题意可得,
计时制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.5x,
包月制:每月应缴费用y(元)与通话时间x(min)的函数关系式是y=0.2x+12;
(2)包月制收费方式比较合算,理由如下:
当x=60时,
计时制:每月应缴费用为:0.5×60=30(元),
包月制:每月应缴费用为:0.2×60+12=24(元),
∵30>24,
∴包月制收费方式比较合算;
(3)当y=100时,0.2x+12=100,
解得x=440.
答:该用户本月可通话440min.
22.解:(1)令x=2,则y=x=1,
∴B的坐标为(2,1),
将A,B两点坐标代入到直线y=kx+b中得,
,
解得,
∴B的坐标为(2,1),k=﹣2,b=5;
(2)证明:∵点A(0,5),B(2,1),
∴OA=5,OB==,AB==2,
∵52=()2+(22),
∴OA2=OB2+AB2,
∴∠ABO=90°,
∴直线y=kx+b与直线y=x互相垂直;
(3)∵△PAB为等腰三角形,
∴可以分三类讨论,
①当BA=BP时,如图,
此时P有两个位置,分别记为P和P′,
由(2)可得,AB=2,
∴PB=2,
设P(p,0),
∴PB==2,
解得:p=2+或p=2﹣,
∴P(2+,0)或P(2﹣,0);
②当AP=AB时,如图,
∵OA⊥x轴,OA=5,AB=2,
∴点A到x轴的距离为5,OA>AB,
∴此时在x轴上不存在点P使△PAB为等腰三角形;
③当PA=PB时,如图,
设P(m,0),
在Rt△POA中,PA2=OA2+OP2=52+m2=25+m2,
同理,PB2=12+(2﹣m)2=m2﹣4m+5,
∵PA=PB,
∴25+m2=m2﹣4m+5,
∴m=﹣5,
∴P(﹣5,0),
∴P(2+,0)或P(2﹣,0)或(﹣5,0).
23.解:(1)设直线AB的解析式是y=kx+b,
根据题意得:,
解得:.
则直线AB的解析式是:y=﹣x+6;
(2)∵A(4,2),C(0,6),
作出点C关于x轴的对称点D(0,﹣6),
∴设直线AD的解析式为y=mx+n,
∴,
∴,
∴直线AD的解析式为y=2x﹣6,
令y=0,则2x﹣6=0,
∴x=3,
∴P(3,0);
(3)存在,理由:
设点Q(a,0),
∵点A(4,2),点O(0,0),
∴AO2=20,AQ2=(a﹣4)2+4,OQ2=a2,
①当AO=AQ时,
∴20=(a﹣4)2+4,
解得:a=8或0(舍去0);
②当AO=OQ时,
∴20=a2,
解得:a=;
③当AQ=OQ时,
∴(a﹣4)2+4=a2,
解得:a=;
故符合条件的点Q坐标为:(﹣2,0)或(2,0)或(8,0)或(,0).
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
