2021-2022学年沪科版七年级数学上册4.1几何图形 课后综合练(word解析版)
文档属性
| 名称 | 2021-2022学年沪科版七年级数学上册4.1几何图形 课后综合练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 16:45:09 | ||
图片预览



文档简介
4.1几何图形【课后综合练】-2021-2022学年七年级数学上册(沪科版)
一、选择题
1、下面的四个几何图形中,表示平面图形的是( )
A. B. C. D.
2、按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是( )
A.B.C. D.
3、在下列几何体中,有( )个棱柱?
A.1 B.2 C.3 D.4
4、如图,几何体圆锥的面数是( )
A.1 B.2 C.3 D.4
5、不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有6条棱,则该模型对应的立体图形可能是( )
A.四棱柱 B.三棱柱 C.四棱锥 D.三棱锥
6、下列三棱柱展开图错误的是( )
A. B. C. D.
7、用一个平面去截四棱柱,截面的形状不可能为( )
A.四边形 B.五边形 C.六边形 D.七边形
8、图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常 B.州 C.越 D.来
9、如图所示的正方体,如果把它展开,可以是下列图形中的( )
A.B.C.D.
10、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有( )种画法.
A.2 B.3 C.4 D.5
二、填空题
11、在一个棱柱中,一共有5个面,则这个棱柱有 条棱,有 个顶点.
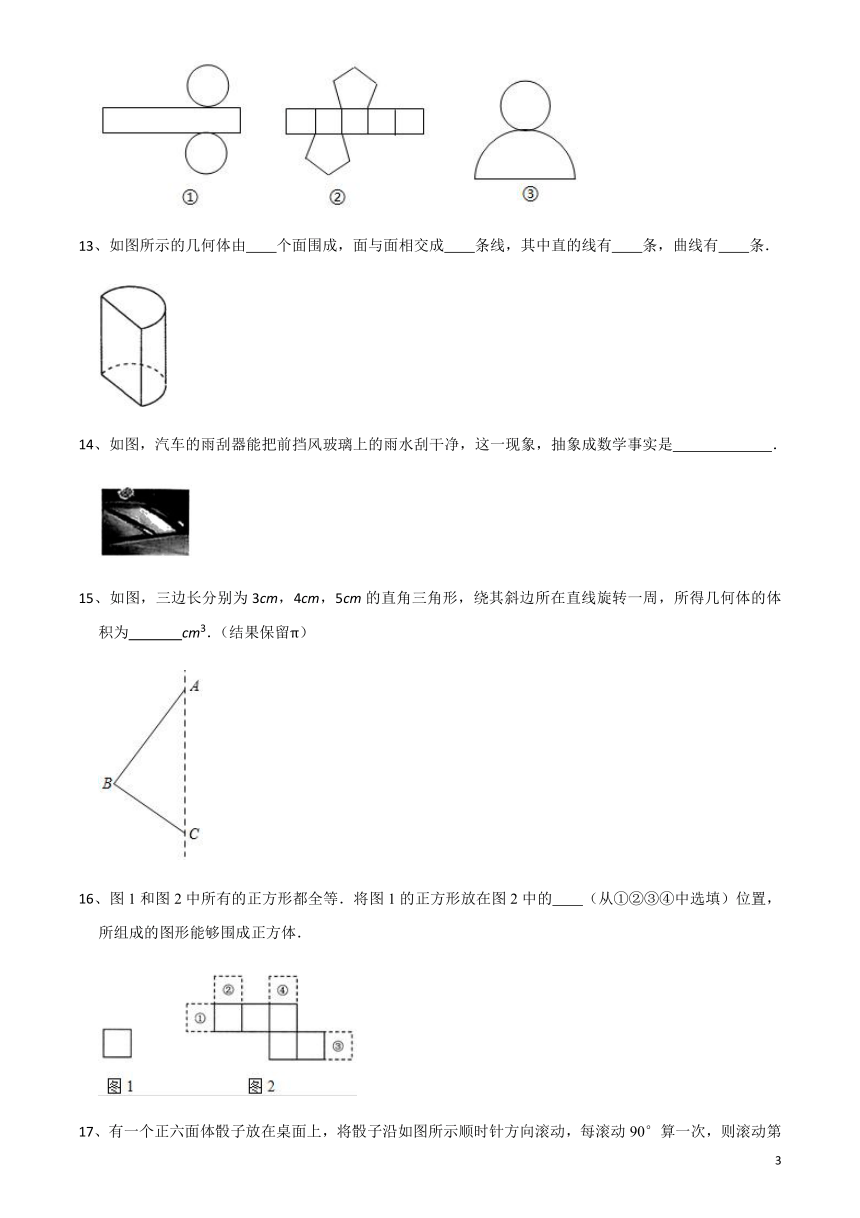
12、如图,下列图形中,①能折叠成 ,②能折叠成 ,③能折叠成 .
13、如图所示的几何体由 个面围成,面与面相交成 条线,其中直的线有 条,曲线有 条.
14、如图,汽车的雨刮器能把前挡风玻璃上的雨水刮干净,这一现象,抽象成数学事实是 .
15、如图,三边长分别为3cm,4cm,5cm的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为 cm3.(结果保留π)
16、图1和图2中所有的正方形都全等.将图1的正方形放在图2中的 (从①②③④中选填)位置,所组成的图形能够围成正方体.
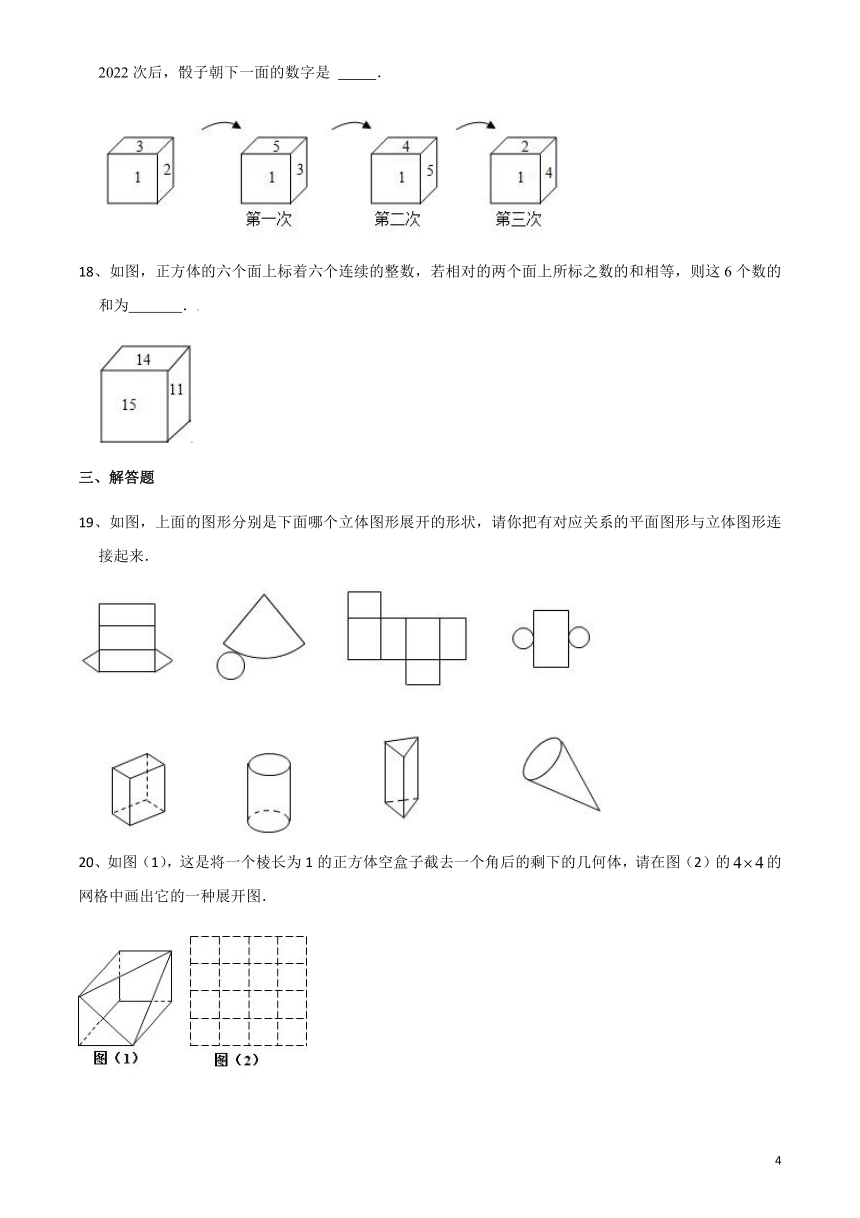
17、有一个正六面体骰子放在桌面上,将骰子沿如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的数字是 .
18、如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
三、解答题
19、如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
20、如图(1),这是将一个棱长为1的正方体空盒子截去一个角后的剩下的几何体,请在图(2)的的网格中画出它的一种展开图.
21、如图,是一个正方体的六个面的展开图形(汉字和数字在正方体外部),回答下列问题:
(1)“0”所对的面是 .
(2)若将其折叠成正方体,如果“7”所在的面在底面,“国”所在的面在后面,则上面是 ;前面是 ;右面是 .
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
22、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
23、如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
24、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
4.1几何图形【课后综合练】-2021-2022学年七年级数学上册(沪科版)(解析)
一、选择题
1、下面的四个几何图形中,表示平面图形的是( )
A. B. C. D.
【答案】D
【分析】
根据平面图形和立体图形的意义,进行判断即可.
【详解】
解:前三个是立体图形,即圆柱体、长方体、球,只有D选项是三角形,是平面图形,
故选:D.
2、按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是( )
A.B.C. D.
【思路点拨】从组成图形的面来考虑即可求解.
【答案】解:正方体,圆柱和四棱柱都是柱体,只有C选项是锥体.
故选:C.
3、在下列几何体中,有( )个棱柱?
A.1 B.2 C.3 D.4
【答案】B
【分析】
根据棱柱的特征进行判断.
【详解】
A、是四棱柱;
B、是圆柱;
C、是三棱柱;
D、是圆锥;
其中棱柱有2个,
故选:B.
4、如图,几何体圆锥的面数是( )
A.1 B.2 C.3 D.4
【答案】B
【分析】
根据圆锥的定义解答即可.
【详解】
解:圆锥是由侧面和底面组成的,所以,圆锥有两个面,
故选:B
5、不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有6条棱,则该模型对应的立体图形可能是( )
A.四棱柱 B.三棱柱 C.四棱锥 D.三棱锥
【答案】D
【分析】
根据三棱锥的特点,可得答案.
【详解】
侧面是三角形,说明它是棱锥,若是棱柱,则侧面应该是长方形,
底面是三角形,说明它是三棱锥,且满足有6条棱的特点,
故选:D.
6、下列三棱柱展开图错误的是( )
A. B. C. D.
【答案】D
【分析】
根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【详解】
解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
7、用一个平面去截四棱柱,截面的形状不可能为( )
A.四边形 B.五边形 C.六边形 D.七边形
【答案】D
【分析】
四棱柱有六个面,用平面去截四棱柱时最多与六个面相交得六边形,最少与三个面相交得三角形.根据此判断即可.
【详解】
用平面去截四棱柱时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
8、图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常 B.州 C.越 D.来
【完整解答】解:由正方体的表面展开图的“相间、Z端是对面”可知,
“常”与“来”是对面,
“州”与“好”是对面,
“越”与“越”是对面,
翻动第1次,第2次时,“好”在前面,“州”在后面,
翻动第3次时,“好”在下面,“州”在上面,
故选:B.
9、如图所示的正方体,如果把它展开,可以是下列图形中的( )
A.B.C.D.
【完整解答】解:由“相间Z端是对面”可知A、D不符合题意,而C折叠后,圆形在前面,正方形在上面,则三角形的面在右面,与原图不符,
只有B折叠后符合,
故选:B.
10、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有( )种画法.
A.2 B.3 C.4 D.5
【答案】B
【分析】根据正方形的展开图的11种形式解答即可.
【详解】解:如图所示;
故答案为B.
二、填空题
11、在一个棱柱中,一共有5个面,则这个棱柱有 条棱,有 个顶点.
【分析】根据棱柱是由5个面围成的,则有2个底面,3个侧面,可得此立体图形是三棱柱,再根据三棱柱的特点可得答案.
【解析】一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
12、如图,下列图形中,①能折叠成 ,②能折叠成 ,③能折叠成 .
【分析】根据圆柱、棱柱、圆锥的展开图形状特点判断即可.
【解析】①能折叠成圆柱,②能折叠成棱柱,③能折叠成圆锥.
故答案为:圆柱,棱柱,圆锥.
13、如图所示的几何体由 个面围成,面与面相交成 条线,其中直的线有 条,曲线有 条.
【思路点拨】根据立体图形的基本知识结合图形即可得出答案.
【答案】解:根据图形可得:如图的几何体有4个面,面与面相交成6条线,直线有4条,曲线有2条.
故答案为:4,6,4,2.
14、如图,汽车的雨刮器能把前挡风玻璃上的雨水刮干净,这一现象,抽象成数学事实是 .
【分析】根据点、线、面的关系,雨刮器是线,运动后形成面.
【答案】解:雨刮器是可以看做线段,线段在运动时形成面,
故答案为线动成面.
15、如图,三边长分别为3cm,4cm,5cm的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为 cm3.(结果保留π)
【分析】根据三角形旋转是圆锥,根据圆锥的体积公式,可得答案.
【解析】如图.
,,
,
几何体的体积为.
故答案为:.
16、图1和图2中所有的正方形都全等.将图1的正方形放在图2中的 (从①②③④中选填)位置,所组成的图形能够围成正方体.
【答案】解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,
将图1的正方形放在图2中的②③④的位置均能围成正方体,
故答案为:②③④.
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.
17、有一个正六面体骰子放在桌面上,将骰子沿如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的数字是 .
【分析】根据滚动的规律,得出每次朝下的一面的数字,进而推断出第2022次朝下一面所对应的数字.
【解答】解:根据滚动规律,从第1次开始朝下的面的数字依次2、3、5、4、2、3、5、4……,
又因为2022÷4=505……2,
所以滚动第2022次后,骰子朝下一面的数字是3,
故答案为:3.
18、如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
【完整解答】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为11,12,13,14,15,16或10,11,12,13,14,15;
且每个相对面上的两个数之和相等,
11+16=27,
10+15=25,
故可能为11,12,13,14,15,16或10,11,12,13,14,15,其和为81和75(11和14必须为对面,在本体图片中,11和14为邻面,故不合题意,应舍去)
故答案为:81.
三、解答题
19、如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【分析】根据常见几何体展开图的形状特征,或折叠成几何体的形状得出判断即可.
【解析】由简单几何体的展开与折叠可得,
20、如图(1),这是将一个棱长为1的正方体空盒子截去一个角后的剩下的几何体,请在图(2)的的网格中画出它的一种展开图.
【答案】见解析
【分析】观察图形,结合正方体展开图的特征,画出它的一个平面展开图即可.
【详解】根据分析画图如下:(画出其中一种就可以)
21、如图,是一个正方体的六个面的展开图形(汉字和数字在正方体外部),回答下列问题:
(1)“0”所对的面是 .
(2)若将其折叠成正方体,如果“7”所在的面在底面,“国”所在的面在后面,则上面是 ;前面是 ;右面是 .
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
【答案】(1)建;(2)周,年,建;(3)7
【分析】
(1)正方体的展开图,相对的面之间一定相隔一个正方形,据此解答即可;
(2)根据正方体的展开图的特点,可先确定“7”与“国”的对面,再确定“7”的右面,进而可得答案;
(3)确定“周”的对面,即为上面不可能的结果.
【详解】
解:(1)“0”所对的面是建;
故答案为:建;
(2)如果“7”所在的面在底面,“国”所在的面在后面,则上面是周;前面是年;右面是建;
故答案为:周,年,建;
(3)将其折叠成正方体,“周”所在的面在前面,则上面不可能是7;
故答案为:7.
22、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
【完整解答】解:(1)由图可得,A与B、C、E、F都相邻,故A对面的字母是D;
E与A、C、D、F都相邻,故B对面的字母是E;
故C的对面是F.
故答案为:D,E,F;
(2)∵字母B表示的数与它对面的字母E表示的数互为相反数,
∴|m﹣3|+(+n)2=0,
∴m﹣3=0,+n=0,
解得m=3,n=﹣,
∴C=m﹣3n﹣=3﹣3×(﹣)﹣=5,
∴F所表示的数是﹣5.
23、如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
【分析】(1)矩形旋转一周得到圆柱;
(2)绕长旋转得到的圆柱的底面半径为3cm,高为4cm,从而计算体积即可;
(3)绕宽旋转得到的圆柱底面半径为4cm,高为3cm,从而计算体积即可.
【答案】解:(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
(2)绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
(3)绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
故答案为:圆柱;面动成体.36πcm3;48πcm3.
24、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
【答案】(1)填表见解析,V+F-E=2;(2)20;(3)14
【分析】(1)观察可得顶点数+面数-棱数=2;(2)代入(1)中的式子即可得到面数;
(3)得到多面体的棱数,求得面数即为x+y的值.
【详解】解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F-E=2;
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
(2)由题意得:F-8+F-30=2,解得F=20;
(3)∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;∴共有24×3÷2=36条棱,
那么24+F-36=2,解得F=14,∴x+y=14.
一、选择题
1、下面的四个几何图形中,表示平面图形的是( )
A. B. C. D.
2、按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是( )
A.B.C. D.
3、在下列几何体中,有( )个棱柱?
A.1 B.2 C.3 D.4
4、如图,几何体圆锥的面数是( )
A.1 B.2 C.3 D.4
5、不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有6条棱,则该模型对应的立体图形可能是( )
A.四棱柱 B.三棱柱 C.四棱锥 D.三棱锥
6、下列三棱柱展开图错误的是( )
A. B. C. D.
7、用一个平面去截四棱柱,截面的形状不可能为( )
A.四边形 B.五边形 C.六边形 D.七边形
8、图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常 B.州 C.越 D.来
9、如图所示的正方体,如果把它展开,可以是下列图形中的( )
A.B.C.D.
10、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有( )种画法.
A.2 B.3 C.4 D.5
二、填空题
11、在一个棱柱中,一共有5个面,则这个棱柱有 条棱,有 个顶点.
12、如图,下列图形中,①能折叠成 ,②能折叠成 ,③能折叠成 .
13、如图所示的几何体由 个面围成,面与面相交成 条线,其中直的线有 条,曲线有 条.
14、如图,汽车的雨刮器能把前挡风玻璃上的雨水刮干净,这一现象,抽象成数学事实是 .
15、如图,三边长分别为3cm,4cm,5cm的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为 cm3.(结果保留π)
16、图1和图2中所有的正方形都全等.将图1的正方形放在图2中的 (从①②③④中选填)位置,所组成的图形能够围成正方体.
17、有一个正六面体骰子放在桌面上,将骰子沿如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的数字是 .
18、如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
三、解答题
19、如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
20、如图(1),这是将一个棱长为1的正方体空盒子截去一个角后的剩下的几何体,请在图(2)的的网格中画出它的一种展开图.
21、如图,是一个正方体的六个面的展开图形(汉字和数字在正方体外部),回答下列问题:
(1)“0”所对的面是 .
(2)若将其折叠成正方体,如果“7”所在的面在底面,“国”所在的面在后面,则上面是 ;前面是 ;右面是 .
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
22、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
23、如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
24、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
4.1几何图形【课后综合练】-2021-2022学年七年级数学上册(沪科版)(解析)
一、选择题
1、下面的四个几何图形中,表示平面图形的是( )
A. B. C. D.
【答案】D
【分析】
根据平面图形和立体图形的意义,进行判断即可.
【详解】
解:前三个是立体图形,即圆柱体、长方体、球,只有D选项是三角形,是平面图形,
故选:D.
2、按柱、锥、球分类,下列几何体中与其余三个不属于同一类几何体的是( )
A.B.C. D.
【思路点拨】从组成图形的面来考虑即可求解.
【答案】解:正方体,圆柱和四棱柱都是柱体,只有C选项是锥体.
故选:C.
3、在下列几何体中,有( )个棱柱?
A.1 B.2 C.3 D.4
【答案】B
【分析】
根据棱柱的特征进行判断.
【详解】
A、是四棱柱;
B、是圆柱;
C、是三棱柱;
D、是圆锥;
其中棱柱有2个,
故选:B.
4、如图,几何体圆锥的面数是( )
A.1 B.2 C.3 D.4
【答案】B
【分析】
根据圆锥的定义解答即可.
【详解】
解:圆锥是由侧面和底面组成的,所以,圆锥有两个面,
故选:B
5、不透明袋子中装有一个几何体模型,两位同学摸该模型并描述它的特征,甲同学:它有4个面是三角形;乙同学:它有6条棱,则该模型对应的立体图形可能是( )
A.四棱柱 B.三棱柱 C.四棱锥 D.三棱锥
【答案】D
【分析】
根据三棱锥的特点,可得答案.
【详解】
侧面是三角形,说明它是棱锥,若是棱柱,则侧面应该是长方形,
底面是三角形,说明它是三棱锥,且满足有6条棱的特点,
故选:D.
6、下列三棱柱展开图错误的是( )
A. B. C. D.
【答案】D
【分析】
根据三棱柱的两底展开是三角形,侧面展开是三个四边形,可得答案.
【详解】
解:A、B、C中间三个长方形能围成三棱柱的侧面,上、下两个三角形围成三棱柱的上、下两底面,故均能围成三棱柱,均是三棱柱的表面展开图.D围成三棱柱时,两个三角形重合为同一底面,而另一底面没有.故D不能围成三棱柱.
故选:D.
7、用一个平面去截四棱柱,截面的形状不可能为( )
A.四边形 B.五边形 C.六边形 D.七边形
【答案】D
【分析】
四棱柱有六个面,用平面去截四棱柱时最多与六个面相交得六边形,最少与三个面相交得三角形.根据此判断即可.
【详解】
用平面去截四棱柱时最多与六个面相交得六边形,因此截面的形状可能是:三角形、四边形、五边形、六边形,不可能是七边形.
故选D.
8、图1是一个小正方体的展开图,小正方体从图2的所示位置依次翻到第1格,第2格,第3格,这时小正方体朝上一面的字是( )
A.常 B.州 C.越 D.来
【完整解答】解:由正方体的表面展开图的“相间、Z端是对面”可知,
“常”与“来”是对面,
“州”与“好”是对面,
“越”与“越”是对面,
翻动第1次,第2次时,“好”在前面,“州”在后面,
翻动第3次时,“好”在下面,“州”在上面,
故选:B.
9、如图所示的正方体,如果把它展开,可以是下列图形中的( )
A.B.C.D.
【完整解答】解:由“相间Z端是对面”可知A、D不符合题意,而C折叠后,圆形在前面,正方形在上面,则三角形的面在右面,与原图不符,
只有B折叠后符合,
故选:B.
10、如图,某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图中阴影部分),但是由于疏忽少画了一个,请你给他补上一个,使之可以组合成正方体,你一共有( )种画法.
A.2 B.3 C.4 D.5
【答案】B
【分析】根据正方形的展开图的11种形式解答即可.
【详解】解:如图所示;
故答案为B.
二、填空题
11、在一个棱柱中,一共有5个面,则这个棱柱有 条棱,有 个顶点.
【分析】根据棱柱是由5个面围成的,则有2个底面,3个侧面,可得此立体图形是三棱柱,再根据三棱柱的特点可得答案.
【解析】一个棱柱中,一共有5个面,则有2个底面,3个侧面,因此此立体图形是三棱柱,则这个棱柱棱的条数有9条,有6个顶点.
故答案为:9;6.
12、如图,下列图形中,①能折叠成 ,②能折叠成 ,③能折叠成 .
【分析】根据圆柱、棱柱、圆锥的展开图形状特点判断即可.
【解析】①能折叠成圆柱,②能折叠成棱柱,③能折叠成圆锥.
故答案为:圆柱,棱柱,圆锥.
13、如图所示的几何体由 个面围成,面与面相交成 条线,其中直的线有 条,曲线有 条.
【思路点拨】根据立体图形的基本知识结合图形即可得出答案.
【答案】解:根据图形可得:如图的几何体有4个面,面与面相交成6条线,直线有4条,曲线有2条.
故答案为:4,6,4,2.
14、如图,汽车的雨刮器能把前挡风玻璃上的雨水刮干净,这一现象,抽象成数学事实是 .
【分析】根据点、线、面的关系,雨刮器是线,运动后形成面.
【答案】解:雨刮器是可以看做线段,线段在运动时形成面,
故答案为线动成面.
15、如图,三边长分别为3cm,4cm,5cm的直角三角形,绕其斜边所在直线旋转一周,所得几何体的体积为 cm3.(结果保留π)
【分析】根据三角形旋转是圆锥,根据圆锥的体积公式,可得答案.
【解析】如图.
,,
,
几何体的体积为.
故答案为:.
16、图1和图2中所有的正方形都全等.将图1的正方形放在图2中的 (从①②③④中选填)位置,所组成的图形能够围成正方体.
【答案】解:将图1的正方形放在图2中的①的位置出现重叠的面,所以不能围成正方体,
将图1的正方形放在图2中的②③④的位置均能围成正方体,
故答案为:②③④.
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.
17、有一个正六面体骰子放在桌面上,将骰子沿如图所示顺时针方向滚动,每滚动90°算一次,则滚动第2022次后,骰子朝下一面的数字是 .
【分析】根据滚动的规律,得出每次朝下的一面的数字,进而推断出第2022次朝下一面所对应的数字.
【解答】解:根据滚动规律,从第1次开始朝下的面的数字依次2、3、5、4、2、3、5、4……,
又因为2022÷4=505……2,
所以滚动第2022次后,骰子朝下一面的数字是3,
故答案为:3.
18、如图,正方体的六个面上标着六个连续的整数,若相对的两个面上所标之数的和相等,则这6个数的和为 .
【完整解答】解:根据题意分析可得:六个面上分别写着六个连续的整数,
故六个整数可能为11,12,13,14,15,16或10,11,12,13,14,15;
且每个相对面上的两个数之和相等,
11+16=27,
10+15=25,
故可能为11,12,13,14,15,16或10,11,12,13,14,15,其和为81和75(11和14必须为对面,在本体图片中,11和14为邻面,故不合题意,应舍去)
故答案为:81.
三、解答题
19、如图,上面的图形分别是下面哪个立体图形展开的形状,请你把有对应关系的平面图形与立体图形连接起来.
【分析】根据常见几何体展开图的形状特征,或折叠成几何体的形状得出判断即可.
【解析】由简单几何体的展开与折叠可得,
20、如图(1),这是将一个棱长为1的正方体空盒子截去一个角后的剩下的几何体,请在图(2)的的网格中画出它的一种展开图.
【答案】见解析
【分析】观察图形,结合正方体展开图的特征,画出它的一个平面展开图即可.
【详解】根据分析画图如下:(画出其中一种就可以)
21、如图,是一个正方体的六个面的展开图形(汉字和数字在正方体外部),回答下列问题:
(1)“0”所对的面是 .
(2)若将其折叠成正方体,如果“7”所在的面在底面,“国”所在的面在后面,则上面是 ;前面是 ;右面是 .
(3)若将其折叠成正方体,“周”所在的面在前面,则上面不可能是 .
【答案】(1)建;(2)周,年,建;(3)7
【分析】
(1)正方体的展开图,相对的面之间一定相隔一个正方形,据此解答即可;
(2)根据正方体的展开图的特点,可先确定“7”与“国”的对面,再确定“7”的右面,进而可得答案;
(3)确定“周”的对面,即为上面不可能的结果.
【详解】
解:(1)“0”所对的面是建;
故答案为:建;
(2)如果“7”所在的面在底面,“国”所在的面在后面,则上面是周;前面是年;右面是建;
故答案为:周,年,建;
(3)将其折叠成正方体,“周”所在的面在前面,则上面不可能是7;
故答案为:7.
22、一个正方体的六个面分别标有字母A、B、C、D、E、F,从三个不同方向看到的情形如图所示.
(1)A的对面是 ,B的对面是 ,C的对面是 ;(直接用字母表示)
(2)若A=﹣2,B=|m﹣3|,C=m﹣3n﹣,E=(+n)2,且小正方体各对面上的两个数都互为相反数,请求出F所表示的数.
【完整解答】解:(1)由图可得,A与B、C、E、F都相邻,故A对面的字母是D;
E与A、C、D、F都相邻,故B对面的字母是E;
故C的对面是F.
故答案为:D,E,F;
(2)∵字母B表示的数与它对面的字母E表示的数互为相反数,
∴|m﹣3|+(+n)2=0,
∴m﹣3=0,+n=0,
解得m=3,n=﹣,
∴C=m﹣3n﹣=3﹣3×(﹣)﹣=5,
∴F所表示的数是﹣5.
23、如图是一个长为4cm,宽为3cm的长方形纸片
(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是 ,这能说明的事实是 .
(2)求:当此长方形纸片绕长边所在直线旋转一周时(如图1),所形成的几何体的体积.
(3)求:当此长方形纸片绕短边所在直线旋转一周时(如图2),所形成的几何体的体积.
【分析】(1)矩形旋转一周得到圆柱;
(2)绕长旋转得到的圆柱的底面半径为3cm,高为4cm,从而计算体积即可;
(3)绕宽旋转得到的圆柱底面半径为4cm,高为3cm,从而计算体积即可.
【答案】解:(1)若将此长方形纸片绕长边或短边所在直线旋转一周,能形成的几何体是圆柱,这能说明的事实是面动成体;
(2)绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;
(3)绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.
故答案为:圆柱;面动成体.36πcm3;48πcm3.
24、十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.
请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
【答案】(1)填表见解析,V+F-E=2;(2)20;(3)14
【分析】(1)观察可得顶点数+面数-棱数=2;(2)代入(1)中的式子即可得到面数;
(3)得到多面体的棱数,求得面数即为x+y的值.
【详解】解:(1)四面体的棱数为6;正八面体的顶点数为6;关系式为:V+F-E=2;
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 4 6
长方体 8 6 12
正八面体 6 8 12
正十二面体 20 12 30
(2)由题意得:F-8+F-30=2,解得F=20;
(3)∵有24个顶点,每个顶点处都有3条棱,两点确定一条直线;∴共有24×3÷2=36条棱,
那么24+F-36=2,解得F=14,∴x+y=14.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
