2021-2022学年华师大版七年级数学上册5.2平行线同步达标测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版七年级数学上册5.2平行线同步达标测试题(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 159.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 17:20:57 | ||
图片预览


文档简介
2021-2022学年华师大版七年级数学上册《5.2平行线》同步达标测试题(附答案)
一.选择题(共10小题,满分30分)
1.下列说法正确的是( )
A.具有公共顶点的两个角是对顶角 B.A、B两点之间的距离就是线段AB
C.两点之间,线段最短 D.不相交的两条直线叫做平行线
2.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
3.如图,下列条件中能判断AD∥BC的是( )
①∠1=∠2;②∠3=∠4;③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.
A.①③④ B.①②④ C.①③ D.①②③④
4.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
5.如图,下面哪个条件不能判断AC∥EF的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
6.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
7.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C,D的位置上,EC交AD于点G,已知∠EFG=57°,则∠BEG等于( )
A.57° B.114° C.66° D.76°
8.如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )
A.15° B.25° C.30° D.45°
9.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm
10.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题(共8小题,满分32分)
11.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
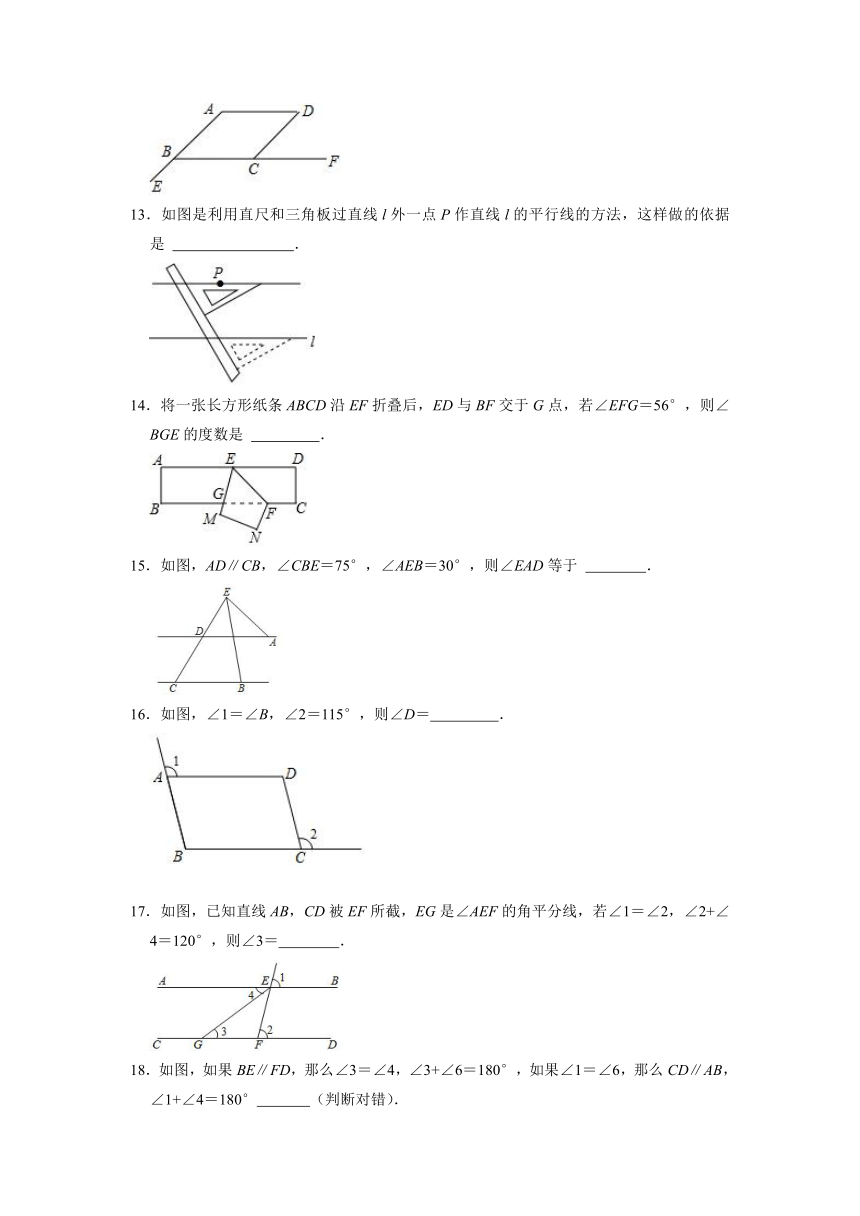
12.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
13.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
14.将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=56°,则∠BGE的度数是 .
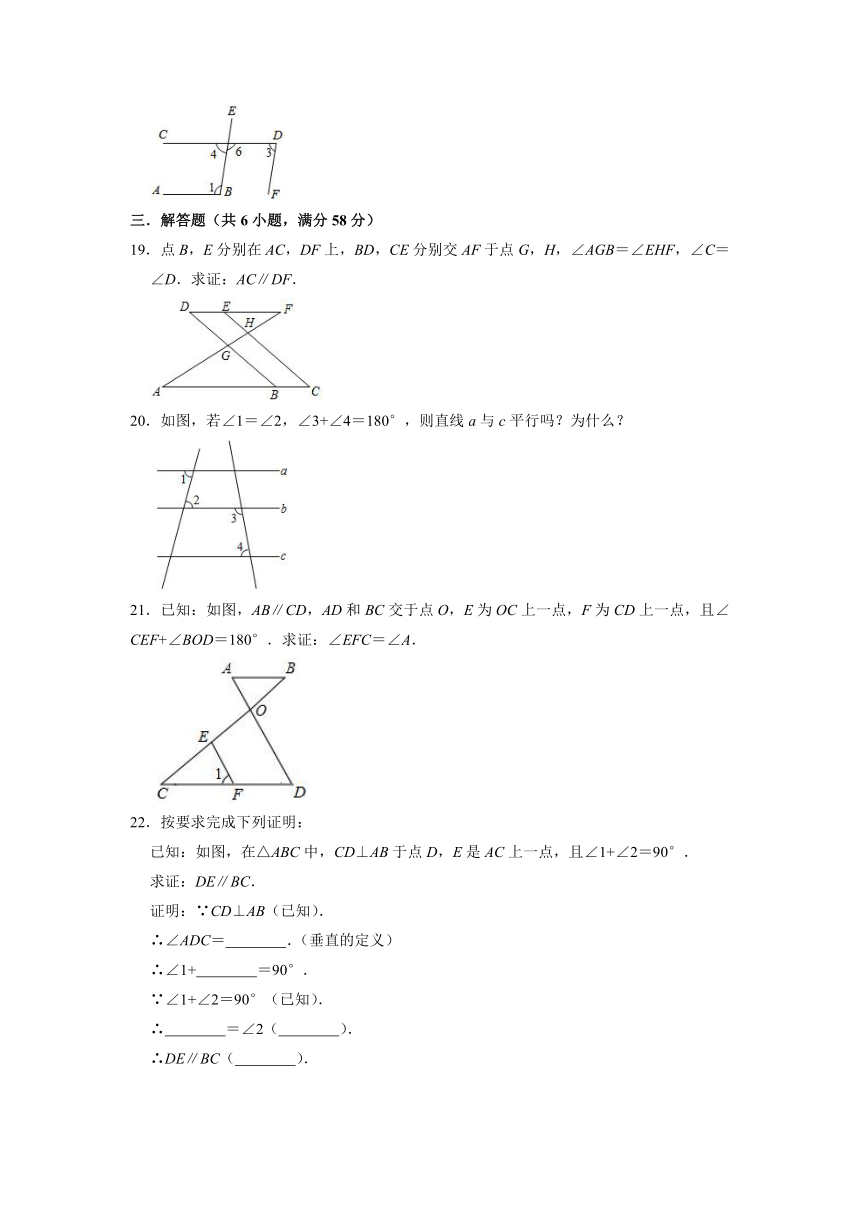
15.如图,AD∥CB,∠CBE=75°,∠AEB=30°,则∠EAD等于 .
16.如图,∠1=∠B,∠2=115°,则∠D= .
17.如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3= .
18.如图,如果BE∥FD,那么∠3=∠4,∠3+∠6=180°,如果∠1=∠6,那么CD∥AB,∠1+∠4=180° (判断对错).
三.解答题(共6小题,满分58分)
19.点B,E分别在AC,DF上,BD,CE分别交AF于点G,H,∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.
20.如图,若∠1=∠2,∠3+∠4=180°,则直线a与c平行吗?为什么?
21.已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
22.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC= .(垂直的定义)
∴∠1+ =90°.
∵∠1+∠2=90°(已知).
∴ =∠2( ).
∴DE∥BC( ).
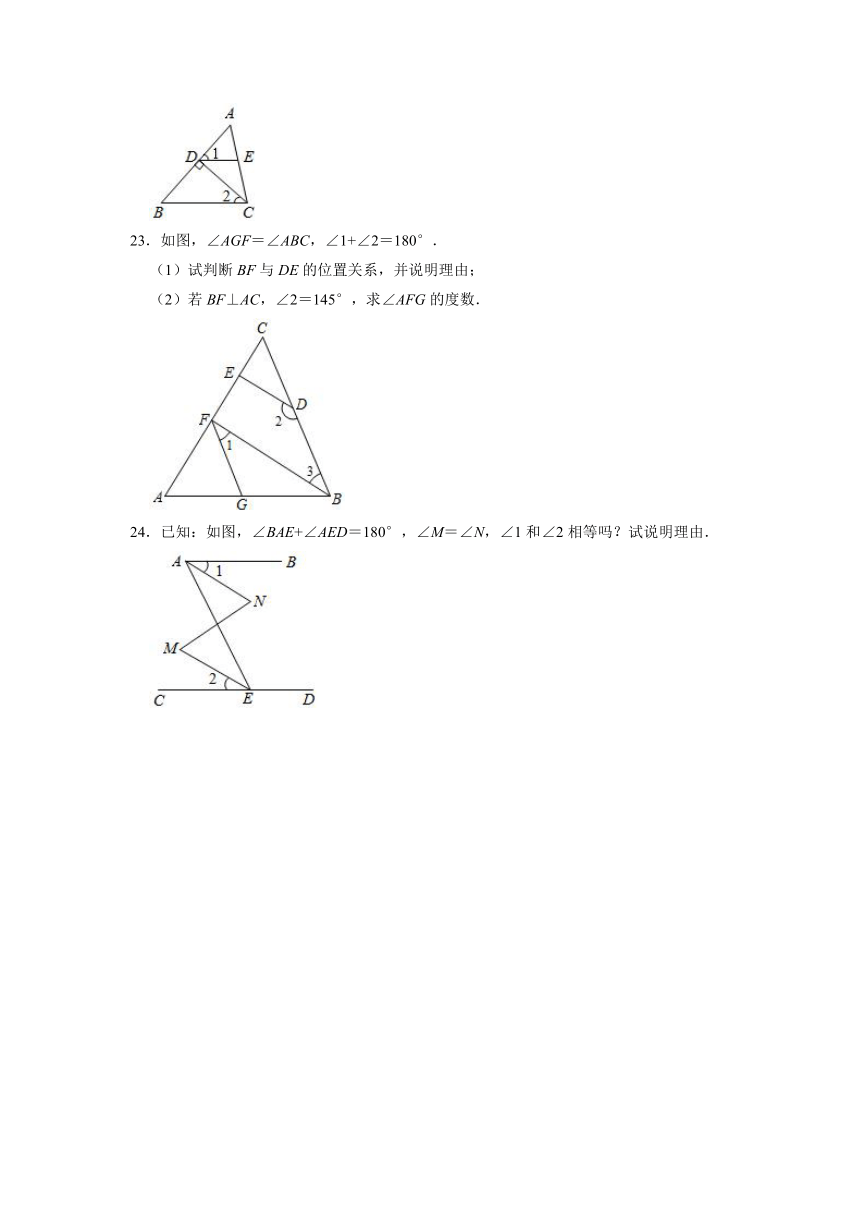
23.如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=145°,求∠AFG的度数.
24.已知:如图,∠BAE+∠AED=180°,∠M=∠N,∠1和∠2相等吗?试说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.具有公共顶点的两个角不一定是对顶角,故本选项错误;
B.A、B两点之间的距离就是线段AB的长,故本选项错误;
C.两点之间,线段最短,故本选项正确;
D.在同一平面内,不相交的两条直线叫做平行线,故本选项错误;
故选:C.
2.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
3.解:①∵∠1=∠2,
∴AD∥BC;
②∵∠3=∠4,
∴AB∥CD;
③∵∠2+∠5=∠6,∠1+∠5=∠6,
∴∠1=∠2,
∴AD∥BC;
④∵∠DAB+∠2+∠3=180°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
可以判断AD∥BC的有①③④.
故选:A.
4.解:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选:B.
5.解:当∠1=∠2时,AC∥EF,故选项A不符合题意;
当∠4=∠C时,AC∥EF,故选项B不符合题意;
当∠1+∠3=180°时,BC∥DE,不能判断AC∥EF,故选项C符合题意;
当∠3+∠C=180°时,AC∥EF,故选项D不符合题意;
故选:C.
6.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
7.解:∵AD∥BC,∠EFG=57°,
∴∠EFG=∠EFC=57°,
由折叠的性质可知,∠EFC=∠FEG,
∴∠GEC=∠EFC+∠FEG=114°,
∴∠BEG=66°.
故选:C.
8.解:∵AB∥CD,
∴∠DNM=∠BME=75°,
∵∠PND=45°,
∴∠PNM=∠DNM﹣∠DNP=30°,
故选:C.
9.解:如图1,直线a和b之间的距离为:5﹣3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).
故选:D.
10.解:∵∠B=∠AGH,
∴GH∥BC,故①正确;
∴∠1=∠HGF,
∵∠1=∠2,
∴∠2=∠HGF,
∴DE∥GF,
∴∠D=∠DMF,
根据已知条件不能推出∠F也等于∠DMF,故②错误;
∵DE∥GF,
∴∠F=∠AHE,
∵∠D=∠1=∠2,
∴∠2不一定等于∠AHE,故③错误;
∵GF⊥AB,GF∥HE,
∴HE⊥AB,故④正确;
即正确的个数是2,
故选:C.
二.填空题(共8小题,满分32分)
11.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
12.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
13.解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
14.解:根据翻折的性质,得:∠DEF=∠GEF,
∵AD∥BC,
∴∠DEF=∠EFG,∠BGE=∠DEG,
∵∠EFG=56°,
∴∠BGE=2∠DEF=2∠EFG=112°.
故答案为:112°.
15.解:∵AD∥CB,∠CBE=75°,
∴∠EFD=∠CBE=75°,
∵∠EFD是△AEF的外角,
∴∠EFD=∠AEB+∠EAD,
∵∠AEB=30°,
∴∠EAD=∠EFD﹣∠AEB=75°﹣30°=45°,
故答案为:45°.
16.解:∵∠1=∠B,
∴AD∥BC,
∴∠D=∠2,
∵∠2=115°,
∴∠D=115°,
故答案为:115°.
17.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠4,∠AEF=∠2,
∵EG是∠AEF的角平分线,
∴∠AEF=∠2=2∠4,
∵∠2+∠4=120°,
∴∠4=40°,
∴∠3=40°,
故答案为:40°.
18.解:∵BE∥FD,
∴∠3=∠4,∠3+∠6=180°,
∵∠1=∠6,
∴CD∥AB,
∴∠1+∠4=180°.
故答案为:正确.
三.解答题(共6小题,满分58分)
19.证明:∵∠AGB=∠EHF,∠AGB=∠DGF,
∴∠DGF=∠EHF,
∴EC∥BD,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
20.解:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a∥c(平行于同一直线的两直线互相平行).
21.证明:∵AB∥CD,
∴∠A=∠D,
∵∠CEF+∠BOD=180°,∠BOD+∠DOC=180°,
∴∠CEF=∠DOC.
∴EF∥AD.
∴∠EFC=∠D,
∵∠A=∠D,
∴∠EFC=∠A.
22.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
23.解:(1)BF∥DE.理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)∵∠1+∠2=180°,∠2=145°,
∴∠1=35°,
∴∠AFG=90°﹣35°=55°.
24.解:∠1和∠2相等.
证明:∵∠BAE+∠AED=180°(已知),
∴AB∥CD.
∴∠BAE=∠AEC (两直线平行,内错角相等).
又∵∠M=∠N (已知),
∴AN∥ME (内错角相等,两直线平行).
∴∠NAE=∠AEM (两直线平行,内错角相等).
∴∠BAE﹣∠NAE=∠AEC﹣∠AEM.
即∠1=∠2(等量代换).
故∠1和∠2相等.
一.选择题(共10小题,满分30分)
1.下列说法正确的是( )
A.具有公共顶点的两个角是对顶角 B.A、B两点之间的距离就是线段AB
C.两点之间,线段最短 D.不相交的两条直线叫做平行线
2.下列说法中,正确的个数为( )
(1)过一点有无数条直线与已知直线平行(2)如果a∥b,a∥c,那么b∥c
(3)如果两线段不相交,那么它们就平行(4)如果两直线不相交,那么它们就平行
A.1个 B.2个 C.3个 D.4个
3.如图,下列条件中能判断AD∥BC的是( )
①∠1=∠2;②∠3=∠4;③∠2+∠5=∠6;④∠DAB+∠2+∠3=180°.
A.①③④ B.①②④ C.①③ D.①②③④
4.如图所示,下列判断错误的是( )
A.若∠1=∠3,AD∥BC,则BD是∠ABC的平分线
B.若AD∥BC,则∠1=∠2=∠3
C.若∠3+∠4+∠C=180°,则AD∥BC
D.若∠2=∠3,则AD∥BC
5.如图,下面哪个条件不能判断AC∥EF的是( )
A.∠1=∠2 B.∠4=∠C C.∠1+∠3=180° D.∠3+∠C=180°
6.将一把直尺和一块含30°角的直角三角板按如图所示方式摆放,其中∠CBD=90°,∠BDC=30°,若∠1=78°,则∠2的度数为( )
A.19° B.18° C.17° D.16°
7.如图,把一张长方形纸片ABCD沿EF折叠后,点C,D分别落在C,D的位置上,EC交AD于点G,已知∠EFG=57°,则∠BEG等于( )
A.57° B.114° C.66° D.76°
8.如图,AB∥CD,直线EF分别交AB,CD于M,N两点,将一个含有45°角的直角三角尺按如图所示的方式摆放,若∠EMB=75°,则∠PNM等于( )
A.15° B.25° C.30° D.45°
9.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和b之间的距离是( )
A.2cm B.6cm C.8cm D.2cm或8cm
10.如图,已知GF⊥AB,∠1=∠2,∠B=∠AGH,则下列结论:①GH∥BC;②∠D=∠F;③HE平分∠AHG;④HE⊥AB,其中正确的有( )
A.0个 B.1个 C.2个 D.3个
二.填空题(共8小题,满分32分)
11.如图,已知OM∥a,ON∥a,所以点O、M、N三点共线的理由 .
12.如图,要使AD∥BF,则需要添加的条件是 (写一个即可)
13.如图是利用直尺和三角板过直线l外一点P作直线l的平行线的方法,这样做的依据是 .
14.将一张长方形纸条ABCD沿EF折叠后,ED与BF交于G点,若∠EFG=56°,则∠BGE的度数是 .
15.如图,AD∥CB,∠CBE=75°,∠AEB=30°,则∠EAD等于 .
16.如图,∠1=∠B,∠2=115°,则∠D= .
17.如图,已知直线AB,CD被EF所截,EG是∠AEF的角平分线,若∠1=∠2,∠2+∠4=120°,则∠3= .
18.如图,如果BE∥FD,那么∠3=∠4,∠3+∠6=180°,如果∠1=∠6,那么CD∥AB,∠1+∠4=180° (判断对错).
三.解答题(共6小题,满分58分)
19.点B,E分别在AC,DF上,BD,CE分别交AF于点G,H,∠AGB=∠EHF,∠C=∠D.求证:AC∥DF.
20.如图,若∠1=∠2,∠3+∠4=180°,则直线a与c平行吗?为什么?
21.已知:如图,AB∥CD,AD和BC交于点O,E为OC上一点,F为CD上一点,且∠CEF+∠BOD=180°.求证:∠EFC=∠A.
22.按要求完成下列证明:
已知:如图,在△ABC中,CD⊥AB于点D,E是AC上一点,且∠1+∠2=90°.
求证:DE∥BC.
证明:∵CD⊥AB(已知).
∴∠ADC= .(垂直的定义)
∴∠1+ =90°.
∵∠1+∠2=90°(已知).
∴ =∠2( ).
∴DE∥BC( ).
23.如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=145°,求∠AFG的度数.
24.已知:如图,∠BAE+∠AED=180°,∠M=∠N,∠1和∠2相等吗?试说明理由.
参考答案
一.选择题(共10小题,满分30分)
1.解:A.具有公共顶点的两个角不一定是对顶角,故本选项错误;
B.A、B两点之间的距离就是线段AB的长,故本选项错误;
C.两点之间,线段最短,故本选项正确;
D.在同一平面内,不相交的两条直线叫做平行线,故本选项错误;
故选:C.
2.解:(1)过直线外一点有且只有一条直线与已知直线平行,故错误;
(2)根据平行公理的推论,正确;
(3)线段的长度是有限的,不相交也不一定平行,故错误;
(4)应该是“在同一平面内”,故错误.
正确的只有一个,故选A.
3.解:①∵∠1=∠2,
∴AD∥BC;
②∵∠3=∠4,
∴AB∥CD;
③∵∠2+∠5=∠6,∠1+∠5=∠6,
∴∠1=∠2,
∴AD∥BC;
④∵∠DAB+∠2+∠3=180°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
可以判断AD∥BC的有①③④.
故选:A.
4.解:A、∵AD∥BC,
∴∠2=∠3,
又∵∠1=∠3,
∴∠1=∠2,则BD是∠ABC的平分线;
B、∠2,∠3是直线AD和直线BC被直线BD所截形成的内错角,若AD∥BC,则∠2=∠3,∠1是直线AB和直线AD被直线BD所截形成的角,因此,若AD∥BC,不能证明∠1=∠2=∠3;
C、∠3+∠4+∠C=180°,即同旁内角∠ADC+∠C=180°,则AD∥BC;
D、内错角∠2=∠3,则AD∥BC.
故选:B.
5.解:当∠1=∠2时,AC∥EF,故选项A不符合题意;
当∠4=∠C时,AC∥EF,故选项B不符合题意;
当∠1+∠3=180°时,BC∥DE,不能判断AC∥EF,故选项C符合题意;
当∠3+∠C=180°时,AC∥EF,故选项D不符合题意;
故选:C.
6.解:∵∠CBD=90°,∠1=78°,
∴∠DBE=180°﹣∠CBD﹣∠1=180°﹣90°﹣78°=12°,
∵直尺的两边平行,即EA∥GH,
∴∠BDF=∠DBE=12°,
∵∠BDC=30°,
∴∠2=∠BDC﹣∠BDF=30°﹣12°=18°,
故选:B.
7.解:∵AD∥BC,∠EFG=57°,
∴∠EFG=∠EFC=57°,
由折叠的性质可知,∠EFC=∠FEG,
∴∠GEC=∠EFC+∠FEG=114°,
∴∠BEG=66°.
故选:C.
8.解:∵AB∥CD,
∴∠DNM=∠BME=75°,
∵∠PND=45°,
∴∠PNM=∠DNM﹣∠DNP=30°,
故选:C.
9.解:如图1,直线a和b之间的距离为:5﹣3=2(cm);
如图2,直线a和b之间的距离为:5+3=8(cm).
故选:D.
10.解:∵∠B=∠AGH,
∴GH∥BC,故①正确;
∴∠1=∠HGF,
∵∠1=∠2,
∴∠2=∠HGF,
∴DE∥GF,
∴∠D=∠DMF,
根据已知条件不能推出∠F也等于∠DMF,故②错误;
∵DE∥GF,
∴∠F=∠AHE,
∵∠D=∠1=∠2,
∴∠2不一定等于∠AHE,故③错误;
∵GF⊥AB,GF∥HE,
∴HE⊥AB,故④正确;
即正确的个数是2,
故选:C.
二.填空题(共8小题,满分32分)
11.解:已知OM∥a,ON∥a,所以点O、M、N三点共线的理由:经过直线外一点,有且只有一条直线与这条直线平行.
故答案为:经过直线外一点,有且只有一条直线与这条直线平行.
12.解:当∠A=∠EBC(或∠D=∠DCF或∠A+∠ABC=180°或∠D+∠BCD=180°)时,AD∥BF,
故答案为:∠A=∠EBC(答案不唯一).
13.解:由图形得,有两个相等的同位角存在,
这样做的依据是:同位角相等,两直线平行.
故答案为:同位角相等,两直线平行.
14.解:根据翻折的性质,得:∠DEF=∠GEF,
∵AD∥BC,
∴∠DEF=∠EFG,∠BGE=∠DEG,
∵∠EFG=56°,
∴∠BGE=2∠DEF=2∠EFG=112°.
故答案为:112°.
15.解:∵AD∥CB,∠CBE=75°,
∴∠EFD=∠CBE=75°,
∵∠EFD是△AEF的外角,
∴∠EFD=∠AEB+∠EAD,
∵∠AEB=30°,
∴∠EAD=∠EFD﹣∠AEB=75°﹣30°=45°,
故答案为:45°.
16.解:∵∠1=∠B,
∴AD∥BC,
∴∠D=∠2,
∵∠2=115°,
∴∠D=115°,
故答案为:115°.
17.解:∵∠1=∠2,
∴AB∥CD,
∴∠3=∠4,∠AEF=∠2,
∵EG是∠AEF的角平分线,
∴∠AEF=∠2=2∠4,
∵∠2+∠4=120°,
∴∠4=40°,
∴∠3=40°,
故答案为:40°.
18.解:∵BE∥FD,
∴∠3=∠4,∠3+∠6=180°,
∵∠1=∠6,
∴CD∥AB,
∴∠1+∠4=180°.
故答案为:正确.
三.解答题(共6小题,满分58分)
19.证明:∵∠AGB=∠EHF,∠AGB=∠DGF,
∴∠DGF=∠EHF,
∴EC∥BD,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF.
20.解:a∥c,
理由是:∵∠1=∠2(已知),
∴a∥b(内错角相等,两直线平行),
∵∠3+∠4=180°(已知),
∴b∥c(同旁内角互补,两直线平行),
∴a∥c(平行于同一直线的两直线互相平行).
21.证明:∵AB∥CD,
∴∠A=∠D,
∵∠CEF+∠BOD=180°,∠BOD+∠DOC=180°,
∴∠CEF=∠DOC.
∴EF∥AD.
∴∠EFC=∠D,
∵∠A=∠D,
∴∠EFC=∠A.
22.解:证明:∵CD⊥AB(已知),
∴∠ADC=90°(垂直的定义),
∴∠1+∠CDE=90°,
∵∠1+∠2=90°(已知),
∴∠CDE=∠2(同角的余角相等),
∴DE∥BC(内错角相等,两直线平行),
故答案为:90°;∠CDE;∠CDE,同角的余角相等;内错角相等,两直线平行.
23.解:(1)BF∥DE.理由如下:
∵∠AGF=∠ABC,
∴GF∥BC,
∴∠1=∠3,
∵∠1+∠2=180°,
∴∠3+∠2=180°,
∴BF∥DE;
(2)∵∠1+∠2=180°,∠2=145°,
∴∠1=35°,
∴∠AFG=90°﹣35°=55°.
24.解:∠1和∠2相等.
证明:∵∠BAE+∠AED=180°(已知),
∴AB∥CD.
∴∠BAE=∠AEC (两直线平行,内错角相等).
又∵∠M=∠N (已知),
∴AN∥ME (内错角相等,两直线平行).
∴∠NAE=∠AEM (两直线平行,内错角相等).
∴∠BAE﹣∠NAE=∠AEC﹣∠AEM.
即∠1=∠2(等量代换).
故∠1和∠2相等.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
