2021-2022学年鲁教版(五四制)八年级数学上册5.4多边形的内角和与外角和同步测试题(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学上册5.4多边形的内角和与外角和同步测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 00:00:00 | ||
图片预览



文档简介
2021-2022学年鲁教版八年级数学上册《5.4多边形的内角和与外角和》
同步测试题(附答案)
一.选择题(共8小题,满分40分)
1.一个多边形的内角和是720°,这个多边形的边数是( )
A.6 B.7 C.8 D.9
2.若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )
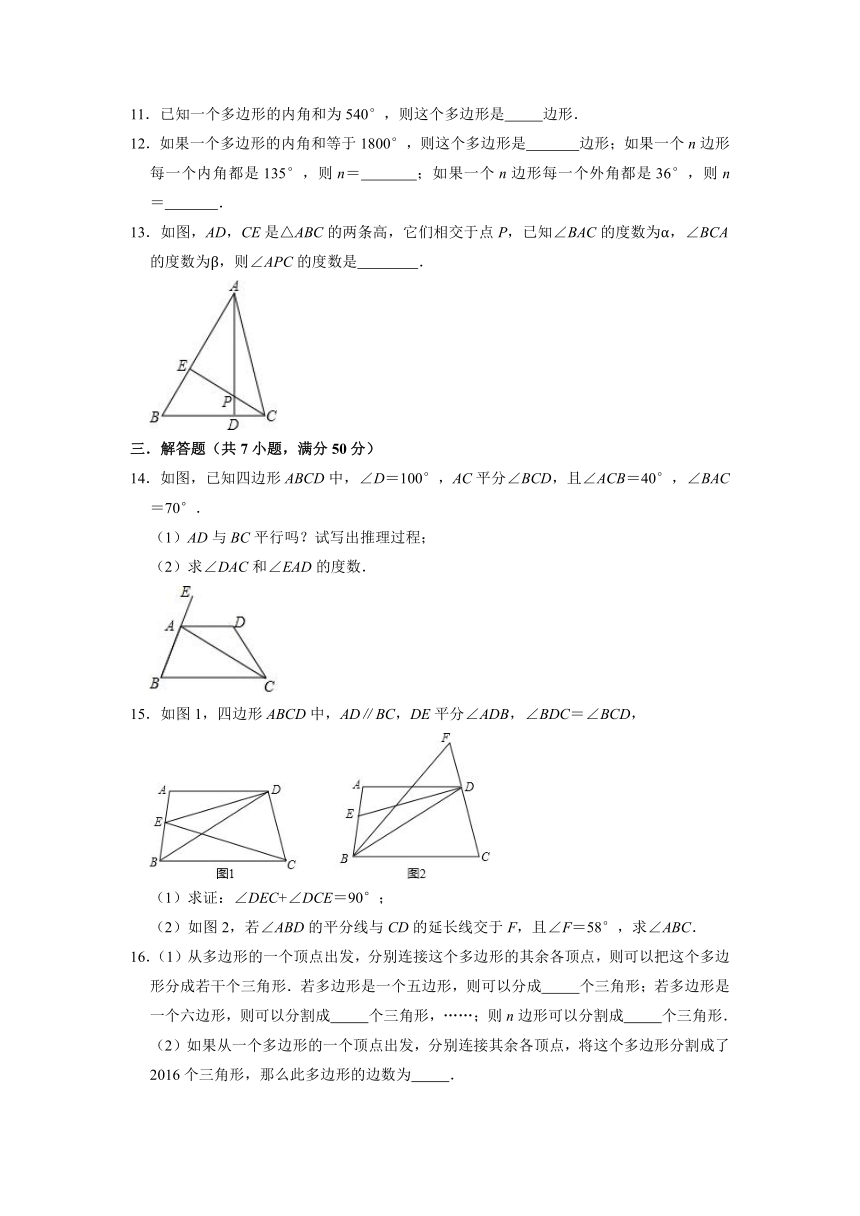
A.三角形 B.四边形 C.五边形 D.六边形
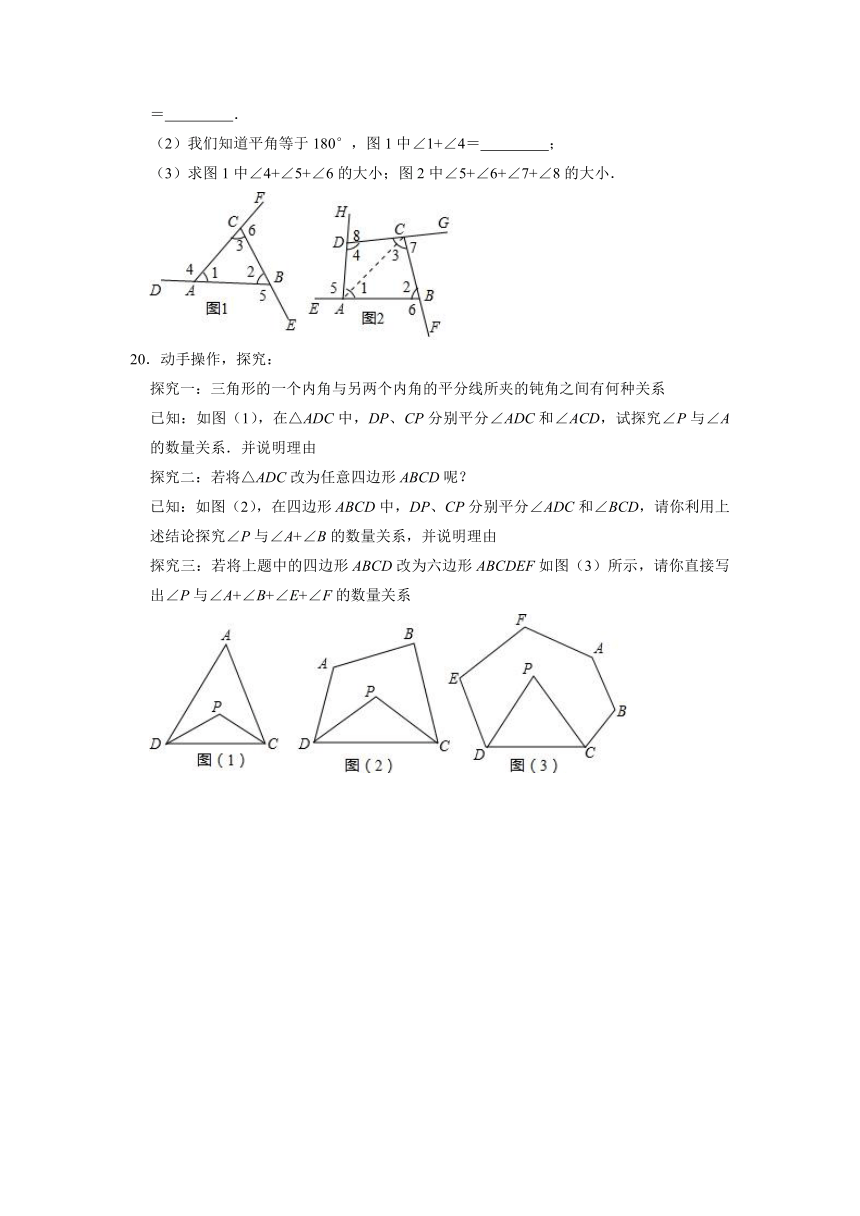
3.一个多边形的边数增加1,则内角和与外角和增加的度数之和是( )
A.60° B.90° C.180° D.360°
4.一个三角形,剪去一个角后所得的多边形内角和的度数是( )
A.180° B.360°
C.540° D.180°或 360°
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.360° B.480° C.540° D.720°
6.从n边形一个顶点出发,可以作( )条对角线.
A.n B.n﹣1 C.n﹣2 D.n﹣3
7.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )
A.8 B.9 C.10 D.12
8.如图,在由等边三角形、正方形和正五边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为( )
A.39° B.40° C.41° D.42°
二.填空题(共5小题,满分30分)
9.若一个多边形的边数为8,则这个多边形的外角和为 .
10.正十边形一个内角度数为 .
11.已知一个多边形的内角和为540°,则这个多边形是 边形.
12.如果一个多边形的内角和等于1800°,则这个多边形是 边形;如果一个n边形每一个内角都是135°,则n= ;如果一个n边形每一个外角都是36°,则n= .
13.如图,AD,CE是△ABC的两条高,它们相交于点P,已知∠BAC的度数为α,∠BCA的度数为β,则∠APC的度数是 .
三.解答题(共7小题,满分50分)
14.如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
15.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
16.(1)从多边形的一个顶点出发,分别连接这个多边形的其余各顶点,则可以把这个多边形分成若干个三角形.若多边形是一个五边形,则可以分成 个三角形;若多边形是一个六边形,则可以分割成 个三角形,……;则n边形可以分割成 个三角形.
(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,那么此多边形的边数为 .
(3)若在n边形的一条边上取一点P(不是顶点),再将点P与n边形的各顶点连接起来,则可将n边形分割成 个三角形.
17.(1)如图1,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
(2)如图2,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角
∠DCE的平分线所在直线相交而形成的锐角.
①如图2,若α+β>180°,求∠P的度数.(用含α,β的代数式表示)
②如图3,若α+β<180°,请在图3中画出∠P,并直接写出∠P的度数.(用含α,β的代数式表示)
18.请你参与下面探究过程,完成所提出的问题.
(1)如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=50°,则∠BPC= °;
(2)如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,直接写出∠BPC与∠A的数量关系 .
(3)如图3,P是四边形ABCD的外角∠EBC与外角∠FCB的平分线BP和CP的交点,设∠A+∠D=α.
①写出∠BPC与α的数量关系;
②根据α的取值范围,直接判断△BPC的形状(按角分类)
19.(1)我们在小学已经学过:三角形的三个内角的和等于180°.如图1中,△ABC的内角和∠1+∠2+∠3=180°,那么在图2中,四边形的内角和∠1+∠2+∠3+∠4= .
(2)我们知道平角等于180°,图1中∠1+∠4= ;
(3)求图1中∠4+∠5+∠6的大小;图2中∠5+∠6+∠7+∠8的大小.
20.动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.并说明理由
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,请你利用上述结论探究∠P与∠A+∠B的数量关系,并说明理由
探究三:若将上题中的四边形ABCD改为六边形ABCDEF如图(3)所示,请你直接写出∠P与∠A+∠B+∠E+∠F的数量关系
参考答案
一.选择题(共8小题,满分40分)
1.解:设这个多边形的边数为n,则
(n﹣2)×180°=720°,
解得n=6,
故这个多边形为六边形.
故选:A.
2.解:设这个多边形的边数为n,由题意,得
(n﹣2) 180=2×360﹣180,
解得n=5;
故选:C.
3.解:由多边形的内角和公式可知:一个多边形边数增加1,则这个多边形内角增加180°;
由任意多边形的外角和是360°可知,外角和增加0°,
则内角和与外角和增加的度数之和是180°.
故选:C.
4.解:剪去一个角,若边数不变,则内角和=(3﹣2) 180°=180°,
若边数增加1,则内角和=(4﹣2) 180°=360°,
所以,所得多边形内角和的度数可能是180°,360°.
故选:D.
5.解:如图,连接AD.
∵∠1=∠E+∠F,∠1=∠FAD+∠ADE,
∴∠E+∠F=∠FAD+∠ADE,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F
=∠BAF+∠B+∠C+∠CDE+∠FAD+∠ADE
=∠BAD+∠B+∠C+∠ADC.
又∵∠BAD+∠B+∠C+∠ADC=360°,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
故选:A.
6.解:n边形(n>3)从一个顶点出发可以引n﹣3条对角线.
故选:D.
7.解:设这个多边形的外角为x°,则内角为3x°,
由题意得:x+3x=180,
解得x=45,
这个多边形的边数:360°÷45°=8,
故选:A.
8.解:等边三角形的内角的度数是60°,正方形的内角度数是90°,
正五边形的内角的度数是:(5﹣2)×180°=108°,
则∠1+∠2=360°﹣60°﹣90°﹣108°﹣∠3=42°.
故选:D.
二.填空题(共5小题,满分30分)
9.解:由任意多边形的外角和为360°可知,这个多边形的外角和为360°.
故答案为:360°.
10.解:∵一个十边形的每个外角都相等,
∴十边形的一个外角为360÷10=36°.
∴每个内角的度数为 180°﹣36°=144°;
故答案为:144°.
11.解:根据多边形的内角和可得:(n﹣2)180°=540°,
解得:n=5.
则这个多边形是五边形.
故答案为:五.
12.解:这个正多边形的边数是n,
则(n﹣2) 180°=1800°,
解得:n=12,
则这个正多边形是12.
如果一个n边形每一个内角都是135°,
∴每一个外角=45°,
则n==8,
如果一个n边形每一个外角都是36°,
则n==10,
故答案为:十二,8,10.
13.解:∠B=180°﹣∠BAC﹣∠ACB=180°﹣(α+β),
∵AD⊥BC,CE⊥AB,
∴∠AEC=∠ADB=90°,
∴∠BAD=90°﹣[180°﹣(α+β)]=α+β﹣90°,
∴∠APC=∠AEC+∠BAD=α+β
故填α+β.
三.解答题(共7小题,满分50分)
14.解:(1)AD∥BC,
理由是:∵AC平分∠BCD,∠ACB=40°,
∴∠BCD=2∠ACB=80°,
∵∠D=100°,
∴∠D+∠BCD=180°,
∴AD∥BC.
(2)∵AD∥BC,∠ACB=40°,
∴∠DAC=∠ACB=40°,
∵∠BAC=70°,
∴∠DAB=∠DAC+∠BAC=40°+70°=110°,
∴∠EAD=180°﹣∠DAB=180°﹣110°=70°.
15.(1)证明:AD∥BC,
∠ADC+∠BCD=180,
∵DE平分∠ADB,
∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°.
(2)解:∵∠FBD+∠BDE=90°﹣∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°.
16.解:(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成5﹣2=3个三角形.
若是一个六边形,可以分割成6﹣2=4个三角形,n边形可以分割成(n﹣2)个三角形.
故答案为:3,4,(n﹣2);
(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,
那么此多边形的边数为:2016+2=2018;
故答案为:2018;
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成(n﹣1)个三角形.
故答案为:(n﹣1).
17.解:(1)∵BP平分∠ABC,
∴∠CBP=∠ABC,
∵CP平分△ABC的外角,
∴∠DCP=∠ACD=(∠A+∠ABC)=∠A+∠ABC,
在△BCP中,由三角形的外角性质,∠DCP=∠CBP+∠P=∠ABC+∠P,
∴∠A+∠ABC=∠ABC+∠P,
∴∠P=∠A=×40°=20°.
(2)①∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠PBC+(180°﹣2∠DCP)=180°﹣2(∠DCP﹣∠FBC)=180°﹣2∠P,
∴360°﹣(α+β)=180°﹣2∠P,
2∠P=α+β﹣180°,
∴∠P=(α+β)﹣90°;
②如图,∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠P,
∴360°﹣(α+β)=180°+2∠P,
∴∠P=90°﹣(α+β).
18.解:(1)∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=65°,
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=115°.
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A),
在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A.
(3)如图3,
①延长BA、CD于Q,
则∠P=90°﹣∠Q,
∴∠Q=180°﹣2∠P,
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°﹣2∠P
=360°﹣2∠P,
∴∠P=180°﹣α;
②当0°<α<180°时,△BPC是钝角三角形,
当α=180°时,△BPC是直角三角形,
当α>180°时,△BPC是锐角三角形.
故答案为:115;∠BPC=90°﹣∠A.
19.解:(1)由图2知,四边形的内角和∠1+∠2+∠3+∠4=180°×2=360°,
故答案为:360°;
(2)图1中∠1+∠4=180°,
故答案为:180°;
(3)∠4+∠5+∠6=180°﹣∠1+180°﹣∠2+180°﹣∠3
=180°×3﹣180°
=180°×2
=360°,
∠5+∠6+∠7+∠8=180°﹣∠1+180°﹣∠2+180°﹣∠3+180°﹣∠4
=180°×4﹣180°×2
=180°×2
=360°.
20.解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠ACD,
=180°﹣(∠ADC+∠ACD),
=180°﹣(180°﹣∠A),
=90°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠BCD,
=180°﹣(∠ADC+∠BCD),
=180°﹣(360°﹣∠A﹣∠B),
=(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6﹣2) 180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣∠EDC﹣∠BCD,
=180°﹣(∠EDC+∠ACD),
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
同步测试题(附答案)
一.选择题(共8小题,满分40分)
1.一个多边形的内角和是720°,这个多边形的边数是( )
A.6 B.7 C.8 D.9
2.若一个多边形的内角和比外角和的2倍少180°,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
3.一个多边形的边数增加1,则内角和与外角和增加的度数之和是( )
A.60° B.90° C.180° D.360°
4.一个三角形,剪去一个角后所得的多边形内角和的度数是( )
A.180° B.360°
C.540° D.180°或 360°
5.如图,∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.360° B.480° C.540° D.720°
6.从n边形一个顶点出发,可以作( )条对角线.
A.n B.n﹣1 C.n﹣2 D.n﹣3
7.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比是3:1,这个多边形的边数是( )
A.8 B.9 C.10 D.12
8.如图,在由等边三角形、正方形和正五边形组合而成的图形中,∠3=60°,则∠1+∠2的度数为( )
A.39° B.40° C.41° D.42°
二.填空题(共5小题,满分30分)
9.若一个多边形的边数为8,则这个多边形的外角和为 .
10.正十边形一个内角度数为 .
11.已知一个多边形的内角和为540°,则这个多边形是 边形.
12.如果一个多边形的内角和等于1800°,则这个多边形是 边形;如果一个n边形每一个内角都是135°,则n= ;如果一个n边形每一个外角都是36°,则n= .
13.如图,AD,CE是△ABC的两条高,它们相交于点P,已知∠BAC的度数为α,∠BCA的度数为β,则∠APC的度数是 .
三.解答题(共7小题,满分50分)
14.如图,已知四边形ABCD中,∠D=100°,AC平分∠BCD,且∠ACB=40°,∠BAC=70°.
(1)AD与BC平行吗?试写出推理过程;
(2)求∠DAC和∠EAD的度数.
15.如图1,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠DEC+∠DCE=90°;
(2)如图2,若∠ABD的平分线与CD的延长线交于F,且∠F=58°,求∠ABC.
16.(1)从多边形的一个顶点出发,分别连接这个多边形的其余各顶点,则可以把这个多边形分成若干个三角形.若多边形是一个五边形,则可以分成 个三角形;若多边形是一个六边形,则可以分割成 个三角形,……;则n边形可以分割成 个三角形.
(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,那么此多边形的边数为 .
(3)若在n边形的一条边上取一点P(不是顶点),再将点P与n边形的各顶点连接起来,则可将n边形分割成 个三角形.
17.(1)如图1,△ABC的内角∠ABC的平分线与外角∠ACD的平分线相交于P点,∠A=40°,求∠P的度数.
(2)如图2,四边形ABCD中,设∠A=α,∠D=β,∠P为四边形ABCD的内角∠ABC与外角
∠DCE的平分线所在直线相交而形成的锐角.
①如图2,若α+β>180°,求∠P的度数.(用含α,β的代数式表示)
②如图3,若α+β<180°,请在图3中画出∠P,并直接写出∠P的度数.(用含α,β的代数式表示)
18.请你参与下面探究过程,完成所提出的问题.
(1)如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=50°,则∠BPC= °;
(2)如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,直接写出∠BPC与∠A的数量关系 .
(3)如图3,P是四边形ABCD的外角∠EBC与外角∠FCB的平分线BP和CP的交点,设∠A+∠D=α.
①写出∠BPC与α的数量关系;
②根据α的取值范围,直接判断△BPC的形状(按角分类)
19.(1)我们在小学已经学过:三角形的三个内角的和等于180°.如图1中,△ABC的内角和∠1+∠2+∠3=180°,那么在图2中,四边形的内角和∠1+∠2+∠3+∠4= .
(2)我们知道平角等于180°,图1中∠1+∠4= ;
(3)求图1中∠4+∠5+∠6的大小;图2中∠5+∠6+∠7+∠8的大小.
20.动手操作,探究:
探究一:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系
已知:如图(1),在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.并说明理由
探究二:若将△ADC改为任意四边形ABCD呢?
已知:如图(2),在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,请你利用上述结论探究∠P与∠A+∠B的数量关系,并说明理由
探究三:若将上题中的四边形ABCD改为六边形ABCDEF如图(3)所示,请你直接写出∠P与∠A+∠B+∠E+∠F的数量关系
参考答案
一.选择题(共8小题,满分40分)
1.解:设这个多边形的边数为n,则
(n﹣2)×180°=720°,
解得n=6,
故这个多边形为六边形.
故选:A.
2.解:设这个多边形的边数为n,由题意,得
(n﹣2) 180=2×360﹣180,
解得n=5;
故选:C.
3.解:由多边形的内角和公式可知:一个多边形边数增加1,则这个多边形内角增加180°;
由任意多边形的外角和是360°可知,外角和增加0°,
则内角和与外角和增加的度数之和是180°.
故选:C.
4.解:剪去一个角,若边数不变,则内角和=(3﹣2) 180°=180°,
若边数增加1,则内角和=(4﹣2) 180°=360°,
所以,所得多边形内角和的度数可能是180°,360°.
故选:D.
5.解:如图,连接AD.
∵∠1=∠E+∠F,∠1=∠FAD+∠ADE,
∴∠E+∠F=∠FAD+∠ADE,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F
=∠BAF+∠B+∠C+∠CDE+∠FAD+∠ADE
=∠BAD+∠B+∠C+∠ADC.
又∵∠BAD+∠B+∠C+∠ADC=360°,
∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°.
故选:A.
6.解:n边形(n>3)从一个顶点出发可以引n﹣3条对角线.
故选:D.
7.解:设这个多边形的外角为x°,则内角为3x°,
由题意得:x+3x=180,
解得x=45,
这个多边形的边数:360°÷45°=8,
故选:A.
8.解:等边三角形的内角的度数是60°,正方形的内角度数是90°,
正五边形的内角的度数是:(5﹣2)×180°=108°,
则∠1+∠2=360°﹣60°﹣90°﹣108°﹣∠3=42°.
故选:D.
二.填空题(共5小题,满分30分)
9.解:由任意多边形的外角和为360°可知,这个多边形的外角和为360°.
故答案为:360°.
10.解:∵一个十边形的每个外角都相等,
∴十边形的一个外角为360÷10=36°.
∴每个内角的度数为 180°﹣36°=144°;
故答案为:144°.
11.解:根据多边形的内角和可得:(n﹣2)180°=540°,
解得:n=5.
则这个多边形是五边形.
故答案为:五.
12.解:这个正多边形的边数是n,
则(n﹣2) 180°=1800°,
解得:n=12,
则这个正多边形是12.
如果一个n边形每一个内角都是135°,
∴每一个外角=45°,
则n==8,
如果一个n边形每一个外角都是36°,
则n==10,
故答案为:十二,8,10.
13.解:∠B=180°﹣∠BAC﹣∠ACB=180°﹣(α+β),
∵AD⊥BC,CE⊥AB,
∴∠AEC=∠ADB=90°,
∴∠BAD=90°﹣[180°﹣(α+β)]=α+β﹣90°,
∴∠APC=∠AEC+∠BAD=α+β
故填α+β.
三.解答题(共7小题,满分50分)
14.解:(1)AD∥BC,
理由是:∵AC平分∠BCD,∠ACB=40°,
∴∠BCD=2∠ACB=80°,
∵∠D=100°,
∴∠D+∠BCD=180°,
∴AD∥BC.
(2)∵AD∥BC,∠ACB=40°,
∴∠DAC=∠ACB=40°,
∵∠BAC=70°,
∴∠DAB=∠DAC+∠BAC=40°+70°=110°,
∴∠EAD=180°﹣∠DAB=180°﹣110°=70°.
15.(1)证明:AD∥BC,
∠ADC+∠BCD=180,
∵DE平分∠ADB,
∠BDC=∠BCD,
∴∠ADE=∠EDB,
∠BDC=∠BCD,
∵∠ADC+∠BCD=180°,
∴∠EDB+∠BDC=90°,
∴∠DEC+∠DCE=90°.
(2)解:∵∠FBD+∠BDE=90°﹣∠F=32°,DE平分∠ADB,BF平分∠ABD,
∴∠ADB+∠ABD=2(∠FBD+∠BDE)=64°,
又∵四边形ABCD中,AD∥BC,
∴∠DBC=∠ADB,
∴∠ABC=∠ABD+∠DBC=∠ABD+∠ADB,即∠ABC=64°.
16.解:(1)从一个五边形的同一顶点出发,分别连接这个顶点与其余各顶点,可以把这个五边形分成5﹣2=3个三角形.
若是一个六边形,可以分割成6﹣2=4个三角形,n边形可以分割成(n﹣2)个三角形.
故答案为:3,4,(n﹣2);
(2)如果从一个多边形的一个顶点出发,分别连接其余各顶点,将这个多边形分割成了2016个三角形,
那么此多边形的边数为:2016+2=2018;
故答案为:2018;
(3)若点P取在多边形的一条边上(不是顶点),在将P与n边形各顶点连接起来,则可将多边形分割成(n﹣1)个三角形.
故答案为:(n﹣1).
17.解:(1)∵BP平分∠ABC,
∴∠CBP=∠ABC,
∵CP平分△ABC的外角,
∴∠DCP=∠ACD=(∠A+∠ABC)=∠A+∠ABC,
在△BCP中,由三角形的外角性质,∠DCP=∠CBP+∠P=∠ABC+∠P,
∴∠A+∠ABC=∠ABC+∠P,
∴∠P=∠A=×40°=20°.
(2)①∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠PBC+(180°﹣2∠DCP)=180°﹣2(∠DCP﹣∠FBC)=180°﹣2∠P,
∴360°﹣(α+β)=180°﹣2∠P,
2∠P=α+β﹣180°,
∴∠P=(α+β)﹣90°;
②如图,∵∠ABC+∠DCB=360°﹣(α+β),
∴∠ABC+(180°﹣∠DCE)=360°﹣(α+β)=2∠GBC+(180°﹣2∠HCE)=180°+2(∠GBC﹣∠HCE)=180°+2∠P,
∴360°﹣(α+β)=180°+2∠P,
∴∠P=90°﹣(α+β).
18.解:(1)∵∠A=50°,
∴∠ABC+∠ACB=130°,
∵BP、CP是角平分线,
∴∠ABC=2∠PBC,∠ACB=2∠BCP,
∴∠PBC+∠BCP=65°,
∵∠PBC+∠BCP+∠BPC=180°,
∴∠BPC=115°.
(2)∵BP,CP分别是外角∠DBC,∠ECB的平分线,
∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A),
在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A.
(3)如图3,
①延长BA、CD于Q,
则∠P=90°﹣∠Q,
∴∠Q=180°﹣2∠P,
∴∠BAD+∠CDA
=180°+∠Q
=180°+180°﹣2∠P
=360°﹣2∠P,
∴∠P=180°﹣α;
②当0°<α<180°时,△BPC是钝角三角形,
当α=180°时,△BPC是直角三角形,
当α>180°时,△BPC是锐角三角形.
故答案为:115;∠BPC=90°﹣∠A.
19.解:(1)由图2知,四边形的内角和∠1+∠2+∠3+∠4=180°×2=360°,
故答案为:360°;
(2)图1中∠1+∠4=180°,
故答案为:180°;
(3)∠4+∠5+∠6=180°﹣∠1+180°﹣∠2+180°﹣∠3
=180°×3﹣180°
=180°×2
=360°,
∠5+∠6+∠7+∠8=180°﹣∠1+180°﹣∠2+180°﹣∠3+180°﹣∠4
=180°×4﹣180°×2
=180°×2
=360°.
20.解:探究一:∵DP、CP分别平分∠ADC和∠ACD,
∴∠PDC=∠ADC,∠PCD=∠ACD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠ACD,
=180°﹣(∠ADC+∠ACD),
=180°﹣(180°﹣∠A),
=90°+∠A;
探究二:∵DP、CP分别平分∠ADC和∠BCD,
∴∠PDC=∠ADC,∠PCD=∠BCD,
∴∠DPC=180°﹣∠PDC﹣∠PCD,
=180°﹣∠ADC﹣∠BCD,
=180°﹣(∠ADC+∠BCD),
=180°﹣(360°﹣∠A﹣∠B),
=(∠A+∠B);
探究三:六边形ABCDEF的内角和为:(6﹣2) 180°=720°,
∵DP、CP分别平分∠EDC和∠BCD,
∴∠PDC=∠EDC,∠PCD=∠BCD,
∴∠P=180°﹣∠PDC﹣∠PCD,
=180°﹣∠EDC﹣∠BCD,
=180°﹣(∠EDC+∠ACD),
=180°﹣(720°﹣∠A﹣∠B﹣∠E﹣∠F),
=(∠A+∠B+∠E+∠F)﹣180°,
即∠P=(∠A+∠B+∠E+∠F)﹣180°.
