2021-2022学年鲁教版(五四制)八年级数学上册5.4多边形的内角和与外角和+同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)八年级数学上册5.4多边形的内角和与外角和+同步达标训练(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 260.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 00:00:00 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学上册《5.4多边形的内角和与外角和》
同步达标训练(附答案)
1.如图,小亮从P点出发,沿直线前进10m后向左转30°,再沿直线前进10m,又向左转30°,……,照这样走下去,他第一次回到出发点P时,一共走了( )
A.100m B.120m C.140m D.300m
2.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60° B.70° C.80° D.90°
3.将一个多边形切去一个角后所得的多边形内角和为2880°,则原多边形的边数为( )
A.15或16 B.15或16或17 C.16或17或18 D.17或18或19
4.一个正六边形的每一个外角都等于( )
A.60° B.72° C.90° D.108°
5.若一个正多边形的每个内角度数都为108°,则这个正多边形的边数是( )
A.5 B.6 C.8 D.10
6.如图,在正六边形ABCDEF中,连接BF,DF,则∠BFD的度数为( )
A.50° B.60° C.65° D.70°
7.正八边形的外角和为( )
A.360° B.720° C.900° D.1080°
8.已知一个多边形的内角和与外角和的和为1980°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
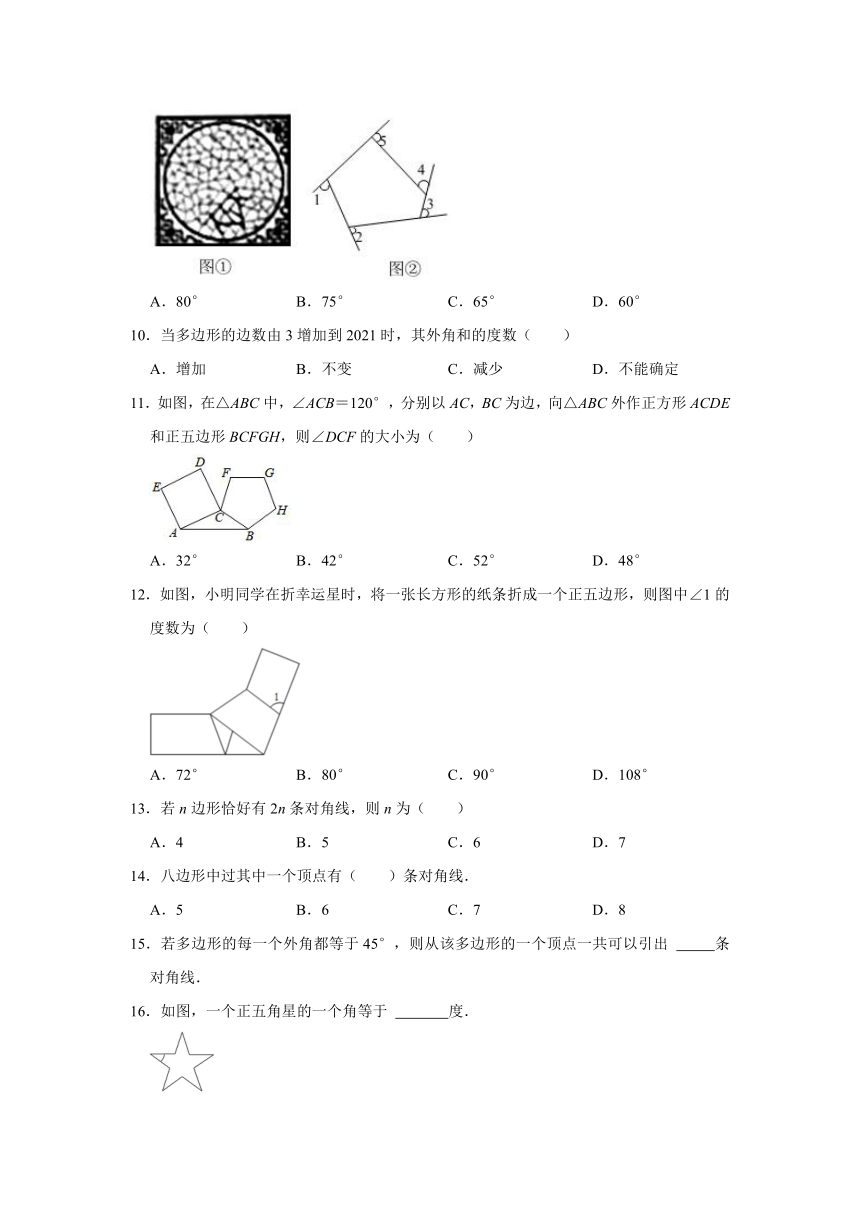
9.“花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.图①中的窗棂是冰裂纹窗,图②是这种窗棂中的部分图案.若∠1=∠2=75°,∠3=∠4=65°,则∠5的度数是( )
A.80° B.75° C.65° D.60°
10.当多边形的边数由3增加到2021时,其外角和的度数( )
A.增加 B.不变 C.减少 D.不能确定
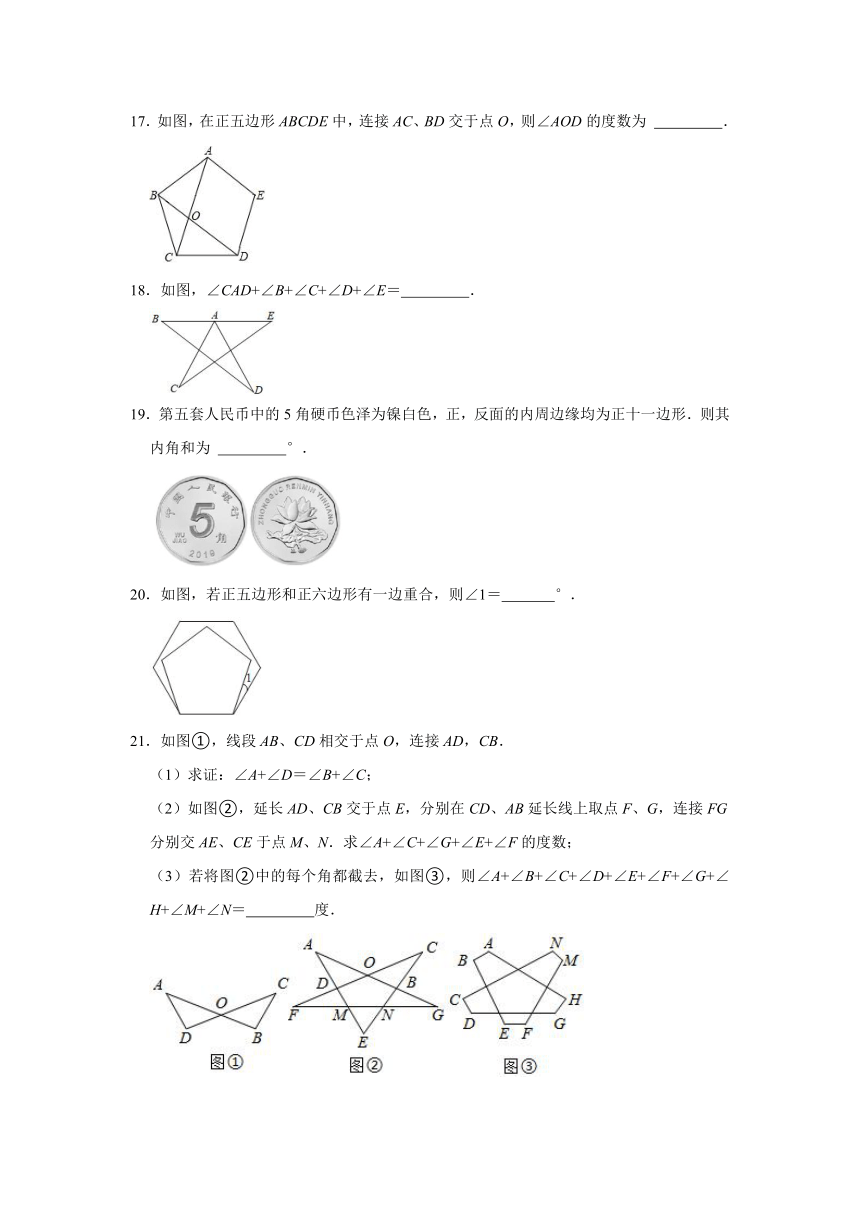
11.如图,在△ABC中,∠ACB=120°,分别以AC,BC为边,向△ABC外作正方形ACDE和正五边形BCFGH,则∠DCF的大小为( )
A.32° B.42° C.52° D.48°
12.如图,小明同学在折幸运星时,将一张长方形的纸条折成一个正五边形,则图中∠1的度数为( )
A.72° B.80° C.90° D.108°
13.若n边形恰好有2n条对角线,则n为( )
A.4 B.5 C.6 D.7
14.八边形中过其中一个顶点有( )条对角线.
A.5 B.6 C.7 D.8
15.若多边形的每一个外角都等于45°,则从该多边形的一个顶点一共可以引出 条对角线.
16.如图,一个正五角星的一个角等于 度.
17.如图,在正五边形ABCDE中,连接AC、BD交于点O,则∠AOD的度数为 .
18.如图,∠CAD+∠B+∠C+∠D+∠E= .
19.第五套人民币中的5角硬币色泽为镍白色,正,反面的内周边缘均为正十一边形.则其内角和为 °.
20.如图,若正五边形和正六边形有一边重合,则∠1= °.
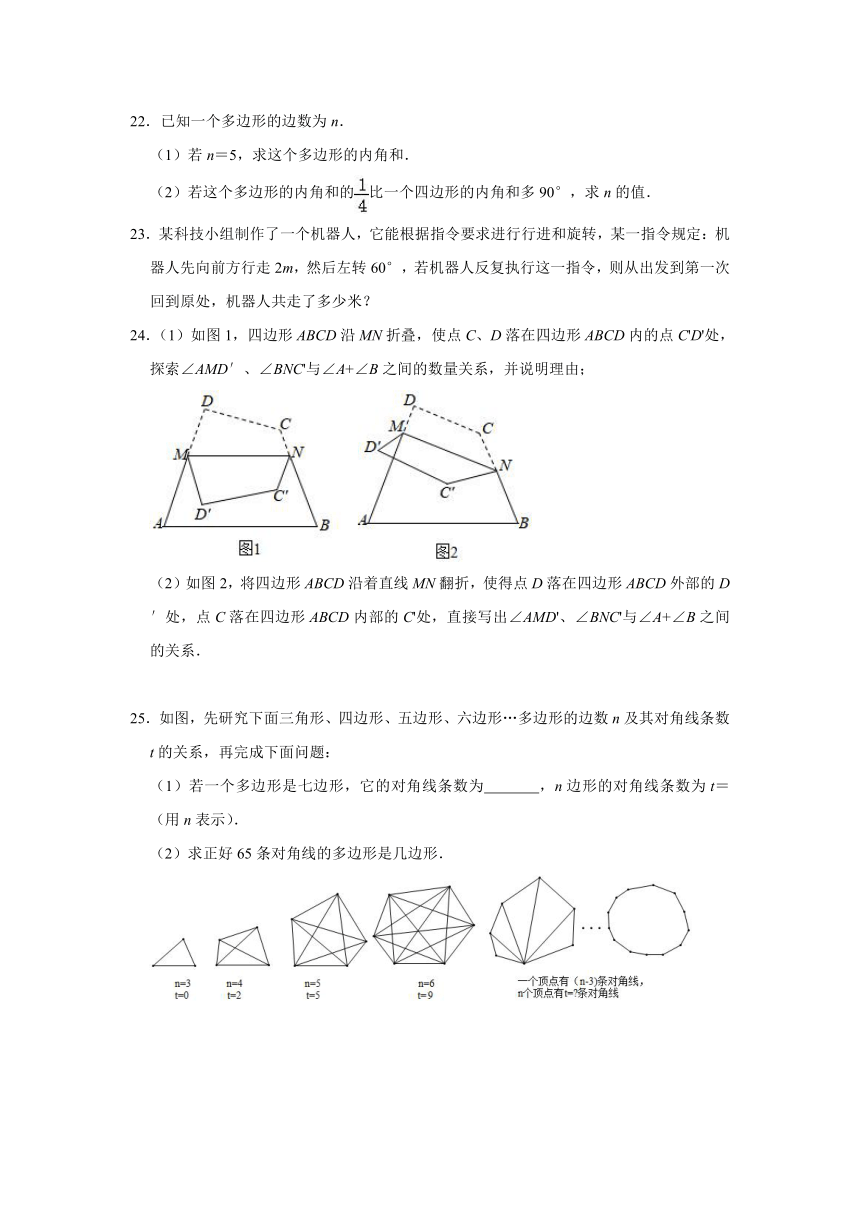
21.如图①,线段AB、CD相交于点O,连接AD,CB.
(1)求证:∠A+∠D=∠B+∠C;
(2)如图②,延长AD、CB交于点E,分别在CD、AB延长线上取点F、G,连接FG分别交AE、CE于点M、N.求∠A+∠C+∠G+∠E+∠F的度数;
(3)若将图②中的每个角都截去,如图③,则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= 度.
22.已知一个多边形的边数为n.
(1)若n=5,求这个多边形的内角和.
(2)若这个多边形的内角和的比一个四边形的内角和多90°,求n的值.
23.某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?
24.(1)如图1,四边形ABCD沿MN折叠,使点C、D落在四边形ABCD内的点C'D'处,探索∠AMD′、∠BNC'与∠A+∠B之间的数量关系,并说明理由;
(2)如图2,将四边形ABCD沿着直线MN翻折,使得点D落在四边形ABCD外部的D′处,点C落在四边形ABCD内部的C'处,直接写出∠AMD'、∠BNC'与∠A+∠B之间的关系.
25.如图,先研究下面三角形、四边形、五边形、六边形…多边形的边数n及其对角线条数t的关系,再完成下面问题:
(1)若一个多边形是七边形,它的对角线条数为 ,n边形的对角线条数为t= (用n表示).
(2)求正好65条对角线的多边形是几边形.
26.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图1,AC、AD是五边形ABCDE的对角线,思考下列问题:
①如图2,多边形A1A2A3A4A5…An.中,过顶点A1可以画 条对角线,过顶点A2可以画 条对角线,过顶点A3可以画 条对角线(用含n的代数式表示)
②过顶点A1的对角线与过顶点A3的对角线中有重复吗?
③在此基础上,你能发现n边形的对角线总条数的规律吗? (用含n的代数式表示)
27.一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.
参考答案
1.解:由题意可知小亮回到原点走了一个正多边形,且每个外角为30°,
∵正多边形的外角和为360°,
∴360°÷30°=12,
∴小亮走了一个正12边形,
∴12×10=120(m),
故选:B.
2.解:设这个多边形的边数为n(n为正整数且n≥3).
由题意得:1180°<180°(n﹣2)<1180°+180°.
∴1180°<180°(n﹣2)<1360°.
∴.
∴n=9.
∴这个多边形的内角和为180°×(9﹣2)=1260°.
∴少算的这个角的度数为1260°﹣1180°=80°.
故选:C.
3.解:设新的多边形的边数为n,
∵新的多边形的内角和是2880°,
∴180(n﹣2)=2880,
解得:n=18,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是18边形,
∴原多边形的边数可能是:17或18或19.
故选:D.
4.解:∵任意多边形的外角和是360°,
∴一个正六边形的每一个外角为:=60°,
故选:A.
5.解:∵多边形的每一个内角都等于108°,多边形的内角与外角互为邻补角,
∴每个外角是:180°﹣108°=72°,
∴多边形中外角的个数是360°÷72°=5,则多边形的边数是5.
故选:A.
6.解:∵六边形ABCDEF是正六边形,
∴∠A=∠AFE=120°,AB=AF.
∴∠ABF=∠AFB.
∴∠ABF+∠AFB=180°﹣∠A=60°.
∴∠ABF=∠AFB=30°.
同理,∠EFD=30°.
∴∠BFD=∠AFE﹣(∠AFB+∠EFD)=120°﹣(30°+30°)=60°.
故选:B.
7.解:∵多边形的外角和都是360°,
∴正八边形的外角和为360°,
故选:A.
8.解:设多边形的边数为n,根据题意列方程得,
(n﹣2) 180°+360°=1980°,
n﹣2=9,
n=11.
故选:C.
9.解:由多边形的外角和等于360°,
可得∠1+∠2+∠3+∠4+∠5=360°,
∵∠1=∠2=75°,∠3=∠4=65°,
∴∠5=360° ∠1 ∠2 ∠3 ∠4,
∴∠5=360° 75° 75° 65° 65°=80°.
故选:A.
10.解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:B.
11.解:∵四边形ACDE是正方形,
∴∠ACD=90°.
∵五边形BCFGH是正五边形,
∴∠FCB=180°﹣=108°.
∴∠DCF=360°﹣∠ACD﹣∠FCB﹣∠ACB=360°﹣90°﹣108°﹣120°=42°.
故选:B.
12.解:由题得:∠1为正五边形的外角.
根据正多边形的性质,每个外角相等,
∴∠1=360°÷5=72°.
故选:A.
13.解:依题意有n(n﹣3)=2n,
∴n(n﹣3)=4n,
整理,得n2﹣7n=0,
即n(n﹣7)=0,
解得n=0(不合题意,舍去)或n=7.
故选:D.
14.解:∵从任意一个n边形的一个顶点出发可得的对角线的条数为(n﹣3)条,
∴八边形中过一个顶点有5条对角线.
故选:A.
15.解:根据题意得:360°÷45°=8,
从这个多边形的一个顶点出发的对角线的条数为:8﹣3=5,
故答案为:5.
16.解:如图,
由三角形外角的性质可得,
∠A+∠C=∠DMN,∠B+∠E=∠DNM,∠D+∠DMN+∠DNM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
∵正五角星每个角相等,
∴一个角的度数是180°÷5=36°.
故答案为:36.
17.解:∵五边形ABCDE是正五边形,
∴AB=BC=CD,∠ABC=∠BCD=180°﹣=108°.
∴∠CBD=∠CDB,∠CBD+∠CDB=180°﹣108°=72°.
∴∠CBD=∠CDB=36°.
同理可得:∠BCA=∠BAC=36°.
∴∠BOC=180°﹣∠DBC﹣∠BCA=180°﹣36°﹣36°=108°.
∵∠BOC与∠AOD是对顶角,
∴∠BOC=∠AOD=108°.
故答案为:108°.
18.解:如图:
∵∠1=∠B+∠D,∠2=∠C+∠CAD,
∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°.
故答案为:180°.
19.解:十一边形的内角和等于:(11﹣2) 180°=1620°.
故答案为:1620.
20.解:正六边形的内角的度数为[(6﹣2)×180°]÷6=120°,
正五边形的内角的度数为[(5﹣2)×180°]÷5=108°,
∴∠1=120°﹣108°=12°.
故答案为12.
21.解:(1)证明:∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,
∵∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B.
(2)如图,连接AC,
∵∠F+∠G+∠FOG=∠OAC+∠OCA+∠AOC=180°,
∠AOC=∠FOG,
∴∠F+∠G=∠OAC+∠OCA,
∵EAC+∠ECA+∠E=180°,
∴∠EAO+∠ECO+∠G+∠E+∠F=180°;
(3)根据(2)可得出规律:在图1中,∠A+∠B+∠C+∠D+∠E=180°,若每截去一个角,则度数会增加180°,所以当截去5个角时,度数会增加(180×5)°,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=l080°.
故答案为1080.
22.解:(1)当n=5时,(5﹣2)×180°=540°. (
∴这个多边形的内角和为540°.
(2)由题意,得,
解得n=12.
∴n的值为12.
23.解:∵机器人向前走2米,然后向左60°,反复执行这一指令,
∴从出发到第一次回到原处,机器人走过的图形是正多边形,
边数=360°÷60°=6,
∴机器人共走了6×2=12(米).
答:从出发到第一次回到原处,机器人共走了12米.
24.解:(1)∠AMD′+∠BNC′=360°﹣2(∠A+∠B),理由如下:
根据四边形的内角和为360°可知,∠D+∠C=360°﹣(∠A+∠B),
∠DMN+∠CNM=360°﹣(∠C+∠D)=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠DMD′+∠CNC′=2(∠A+∠B),
∵∠DMD′+∠AMD′=180°,∠CNC′+∠BNC′=180°,
∴∠AMD′+∠BNC′=360°﹣2(∠A+∠B).
(2)∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B),理由如下:
由(1)知,∠DMN+∠CNM=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠D′MN+∠C′NM=∠A+∠B,
由四边形的内角和为360°得,∠D′MN﹣∠AMD′+∠BNC′+∠C′NM=360°﹣(∠A+∠B)
∴∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B).
25.解:(1)若一个多边形是七边形,它的对角线条数为=14,n边形的对角线条数为t=(用n表示).
(2)设正好65条对角线的多边形是x边形,依题意有
=65,
解得x1=13,x2=﹣10.
故正好65条对角线的多边形是13边形.
故答案为:14,.
26.解:故答案为:(1)(n﹣3);(n﹣3);(n﹣3)
(2)有重复
(3)
27.解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180°×(n﹣2)=1980°,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
①若截去一个角后边数增加1,则原多边形边数为12,
②若截去一个角后边数不变,则原多边形边数为13,
③若截去一个角后边数减少1,则原多边形边数为14,
∴原多边形的边数可能是:12或13或14.
同步达标训练(附答案)
1.如图,小亮从P点出发,沿直线前进10m后向左转30°,再沿直线前进10m,又向左转30°,……,照这样走下去,他第一次回到出发点P时,一共走了( )
A.100m B.120m C.140m D.300m
2.在计算一个多边形的内角和时,由于粗心少算了1个内角,其和等于1180°,则少算的这个角的度数是( )
A.60° B.70° C.80° D.90°
3.将一个多边形切去一个角后所得的多边形内角和为2880°,则原多边形的边数为( )
A.15或16 B.15或16或17 C.16或17或18 D.17或18或19
4.一个正六边形的每一个外角都等于( )
A.60° B.72° C.90° D.108°
5.若一个正多边形的每个内角度数都为108°,则这个正多边形的边数是( )
A.5 B.6 C.8 D.10
6.如图,在正六边形ABCDEF中,连接BF,DF,则∠BFD的度数为( )
A.50° B.60° C.65° D.70°
7.正八边形的外角和为( )
A.360° B.720° C.900° D.1080°
8.已知一个多边形的内角和与外角和的和为1980°,这个多边形的边数为( )
A.9 B.10 C.11 D.12
9.“花影遮墙,峰峦叠窗”苏州园林空透的窗棂中蕴含着许多的数学元素.图①中的窗棂是冰裂纹窗,图②是这种窗棂中的部分图案.若∠1=∠2=75°,∠3=∠4=65°,则∠5的度数是( )
A.80° B.75° C.65° D.60°
10.当多边形的边数由3增加到2021时,其外角和的度数( )
A.增加 B.不变 C.减少 D.不能确定
11.如图,在△ABC中,∠ACB=120°,分别以AC,BC为边,向△ABC外作正方形ACDE和正五边形BCFGH,则∠DCF的大小为( )
A.32° B.42° C.52° D.48°
12.如图,小明同学在折幸运星时,将一张长方形的纸条折成一个正五边形,则图中∠1的度数为( )
A.72° B.80° C.90° D.108°
13.若n边形恰好有2n条对角线,则n为( )
A.4 B.5 C.6 D.7
14.八边形中过其中一个顶点有( )条对角线.
A.5 B.6 C.7 D.8
15.若多边形的每一个外角都等于45°,则从该多边形的一个顶点一共可以引出 条对角线.
16.如图,一个正五角星的一个角等于 度.
17.如图,在正五边形ABCDE中,连接AC、BD交于点O,则∠AOD的度数为 .
18.如图,∠CAD+∠B+∠C+∠D+∠E= .
19.第五套人民币中的5角硬币色泽为镍白色,正,反面的内周边缘均为正十一边形.则其内角和为 °.
20.如图,若正五边形和正六边形有一边重合,则∠1= °.
21.如图①,线段AB、CD相交于点O,连接AD,CB.
(1)求证:∠A+∠D=∠B+∠C;
(2)如图②,延长AD、CB交于点E,分别在CD、AB延长线上取点F、G,连接FG分别交AE、CE于点M、N.求∠A+∠C+∠G+∠E+∠F的度数;
(3)若将图②中的每个角都截去,如图③,则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N= 度.
22.已知一个多边形的边数为n.
(1)若n=5,求这个多边形的内角和.
(2)若这个多边形的内角和的比一个四边形的内角和多90°,求n的值.
23.某科技小组制作了一个机器人,它能根据指令要求进行行进和旋转,某一指令规定:机器人先向前方行走2m,然后左转60°,若机器人反复执行这一指令,则从出发到第一次回到原处,机器人共走了多少米?
24.(1)如图1,四边形ABCD沿MN折叠,使点C、D落在四边形ABCD内的点C'D'处,探索∠AMD′、∠BNC'与∠A+∠B之间的数量关系,并说明理由;
(2)如图2,将四边形ABCD沿着直线MN翻折,使得点D落在四边形ABCD外部的D′处,点C落在四边形ABCD内部的C'处,直接写出∠AMD'、∠BNC'与∠A+∠B之间的关系.
25.如图,先研究下面三角形、四边形、五边形、六边形…多边形的边数n及其对角线条数t的关系,再完成下面问题:
(1)若一个多边形是七边形,它的对角线条数为 ,n边形的对角线条数为t= (用n表示).
(2)求正好65条对角线的多边形是几边形.
26.连接多边形不相邻的两个顶点的线段,叫做多边形的对角线.
如图1,AC、AD是五边形ABCDE的对角线,思考下列问题:
①如图2,多边形A1A2A3A4A5…An.中,过顶点A1可以画 条对角线,过顶点A2可以画 条对角线,过顶点A3可以画 条对角线(用含n的代数式表示)
②过顶点A1的对角线与过顶点A3的对角线中有重复吗?
③在此基础上,你能发现n边形的对角线总条数的规律吗? (用含n的代数式表示)
27.一个多边形剪去一个内角后,得到一个内角和为1980°的新多边形,求原多边形的边数.
参考答案
1.解:由题意可知小亮回到原点走了一个正多边形,且每个外角为30°,
∵正多边形的外角和为360°,
∴360°÷30°=12,
∴小亮走了一个正12边形,
∴12×10=120(m),
故选:B.
2.解:设这个多边形的边数为n(n为正整数且n≥3).
由题意得:1180°<180°(n﹣2)<1180°+180°.
∴1180°<180°(n﹣2)<1360°.
∴.
∴n=9.
∴这个多边形的内角和为180°×(9﹣2)=1260°.
∴少算的这个角的度数为1260°﹣1180°=80°.
故选:C.
3.解:设新的多边形的边数为n,
∵新的多边形的内角和是2880°,
∴180(n﹣2)=2880,
解得:n=18,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是18边形,
∴原多边形的边数可能是:17或18或19.
故选:D.
4.解:∵任意多边形的外角和是360°,
∴一个正六边形的每一个外角为:=60°,
故选:A.
5.解:∵多边形的每一个内角都等于108°,多边形的内角与外角互为邻补角,
∴每个外角是:180°﹣108°=72°,
∴多边形中外角的个数是360°÷72°=5,则多边形的边数是5.
故选:A.
6.解:∵六边形ABCDEF是正六边形,
∴∠A=∠AFE=120°,AB=AF.
∴∠ABF=∠AFB.
∴∠ABF+∠AFB=180°﹣∠A=60°.
∴∠ABF=∠AFB=30°.
同理,∠EFD=30°.
∴∠BFD=∠AFE﹣(∠AFB+∠EFD)=120°﹣(30°+30°)=60°.
故选:B.
7.解:∵多边形的外角和都是360°,
∴正八边形的外角和为360°,
故选:A.
8.解:设多边形的边数为n,根据题意列方程得,
(n﹣2) 180°+360°=1980°,
n﹣2=9,
n=11.
故选:C.
9.解:由多边形的外角和等于360°,
可得∠1+∠2+∠3+∠4+∠5=360°,
∵∠1=∠2=75°,∠3=∠4=65°,
∴∠5=360° ∠1 ∠2 ∠3 ∠4,
∴∠5=360° 75° 75° 65° 65°=80°.
故选:A.
10.解:∵任何多边形的外角和都是360°,
∴多边形的边数由3增加到2021时,其外角和的度数不变,
故选:B.
11.解:∵四边形ACDE是正方形,
∴∠ACD=90°.
∵五边形BCFGH是正五边形,
∴∠FCB=180°﹣=108°.
∴∠DCF=360°﹣∠ACD﹣∠FCB﹣∠ACB=360°﹣90°﹣108°﹣120°=42°.
故选:B.
12.解:由题得:∠1为正五边形的外角.
根据正多边形的性质,每个外角相等,
∴∠1=360°÷5=72°.
故选:A.
13.解:依题意有n(n﹣3)=2n,
∴n(n﹣3)=4n,
整理,得n2﹣7n=0,
即n(n﹣7)=0,
解得n=0(不合题意,舍去)或n=7.
故选:D.
14.解:∵从任意一个n边形的一个顶点出发可得的对角线的条数为(n﹣3)条,
∴八边形中过一个顶点有5条对角线.
故选:A.
15.解:根据题意得:360°÷45°=8,
从这个多边形的一个顶点出发的对角线的条数为:8﹣3=5,
故答案为:5.
16.解:如图,
由三角形外角的性质可得,
∠A+∠C=∠DMN,∠B+∠E=∠DNM,∠D+∠DMN+∠DNM=180°,
∴∠A+∠B+∠C+∠D+∠E=180°,
∵正五角星每个角相等,
∴一个角的度数是180°÷5=36°.
故答案为:36.
17.解:∵五边形ABCDE是正五边形,
∴AB=BC=CD,∠ABC=∠BCD=180°﹣=108°.
∴∠CBD=∠CDB,∠CBD+∠CDB=180°﹣108°=72°.
∴∠CBD=∠CDB=36°.
同理可得:∠BCA=∠BAC=36°.
∴∠BOC=180°﹣∠DBC﹣∠BCA=180°﹣36°﹣36°=108°.
∵∠BOC与∠AOD是对顶角,
∴∠BOC=∠AOD=108°.
故答案为:108°.
18.解:如图:
∵∠1=∠B+∠D,∠2=∠C+∠CAD,
∴∠CAD+∠B+∠C+∠D+∠E=∠1+∠2+∠E=180°.
故答案为:180°.
19.解:十一边形的内角和等于:(11﹣2) 180°=1620°.
故答案为:1620.
20.解:正六边形的内角的度数为[(6﹣2)×180°]÷6=120°,
正五边形的内角的度数为[(5﹣2)×180°]÷5=108°,
∴∠1=120°﹣108°=12°.
故答案为12.
21.解:(1)证明:∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,
∵∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B.
(2)如图,连接AC,
∵∠F+∠G+∠FOG=∠OAC+∠OCA+∠AOC=180°,
∠AOC=∠FOG,
∴∠F+∠G=∠OAC+∠OCA,
∵EAC+∠ECA+∠E=180°,
∴∠EAO+∠ECO+∠G+∠E+∠F=180°;
(3)根据(2)可得出规律:在图1中,∠A+∠B+∠C+∠D+∠E=180°,若每截去一个角,则度数会增加180°,所以当截去5个角时,度数会增加(180×5)°,
则∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=180°×5+180°=l080°.
故答案为1080.
22.解:(1)当n=5时,(5﹣2)×180°=540°. (
∴这个多边形的内角和为540°.
(2)由题意,得,
解得n=12.
∴n的值为12.
23.解:∵机器人向前走2米,然后向左60°,反复执行这一指令,
∴从出发到第一次回到原处,机器人走过的图形是正多边形,
边数=360°÷60°=6,
∴机器人共走了6×2=12(米).
答:从出发到第一次回到原处,机器人共走了12米.
24.解:(1)∠AMD′+∠BNC′=360°﹣2(∠A+∠B),理由如下:
根据四边形的内角和为360°可知,∠D+∠C=360°﹣(∠A+∠B),
∠DMN+∠CNM=360°﹣(∠C+∠D)=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠DMD′+∠CNC′=2(∠A+∠B),
∵∠DMD′+∠AMD′=180°,∠CNC′+∠BNC′=180°,
∴∠AMD′+∠BNC′=360°﹣2(∠A+∠B).
(2)∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B),理由如下:
由(1)知,∠DMN+∠CNM=∠A+∠B,
根据折叠的性质得,∠DMN=∠D′MN,∠CNM=∠C′NM,
∴∠D′MN+∠C′NM=∠A+∠B,
由四边形的内角和为360°得,∠D′MN﹣∠AMD′+∠BNC′+∠C′NM=360°﹣(∠A+∠B)
∴∠BNC′﹣∠AMD′=360°﹣2(∠A+∠B).
25.解:(1)若一个多边形是七边形,它的对角线条数为=14,n边形的对角线条数为t=(用n表示).
(2)设正好65条对角线的多边形是x边形,依题意有
=65,
解得x1=13,x2=﹣10.
故正好65条对角线的多边形是13边形.
故答案为:14,.
26.解:故答案为:(1)(n﹣3);(n﹣3);(n﹣3)
(2)有重复
(3)
27.解:设新的多边形的边数为n,
∵新的多边形的内角和是1980°,
∴180°×(n﹣2)=1980°,
解得:n=13,
∵一个多边形从某一个顶点出发截去一个角后所形成的新的多边形是十三边形,
①若截去一个角后边数增加1,则原多边形边数为12,
②若截去一个角后边数不变,则原多边形边数为13,
③若截去一个角后边数减少1,则原多边形边数为14,
∴原多边形的边数可能是:12或13或14.
