2021-2022学年北师大版八年级数学上册7.5三角形的内角和定理同步达标测试(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册7.5三角形的内角和定理同步达标测试(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 211.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-18 00:00:00 | ||
图片预览

文档简介
2021-2022学年北师大版八年级数学上册《7.5三角形的内角和定理》
同步达标测试(附答案)
一.选择题(共8小题,满分32分)
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2.如图,点A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.180° B.360° C.540° D.720°
3.适合条件∠A=∠B=∠C的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
4.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120° C.130° D.140°
5.如图,在△ABC中,∠ABC=60°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
6.下列条件中,能判定△ABC为直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
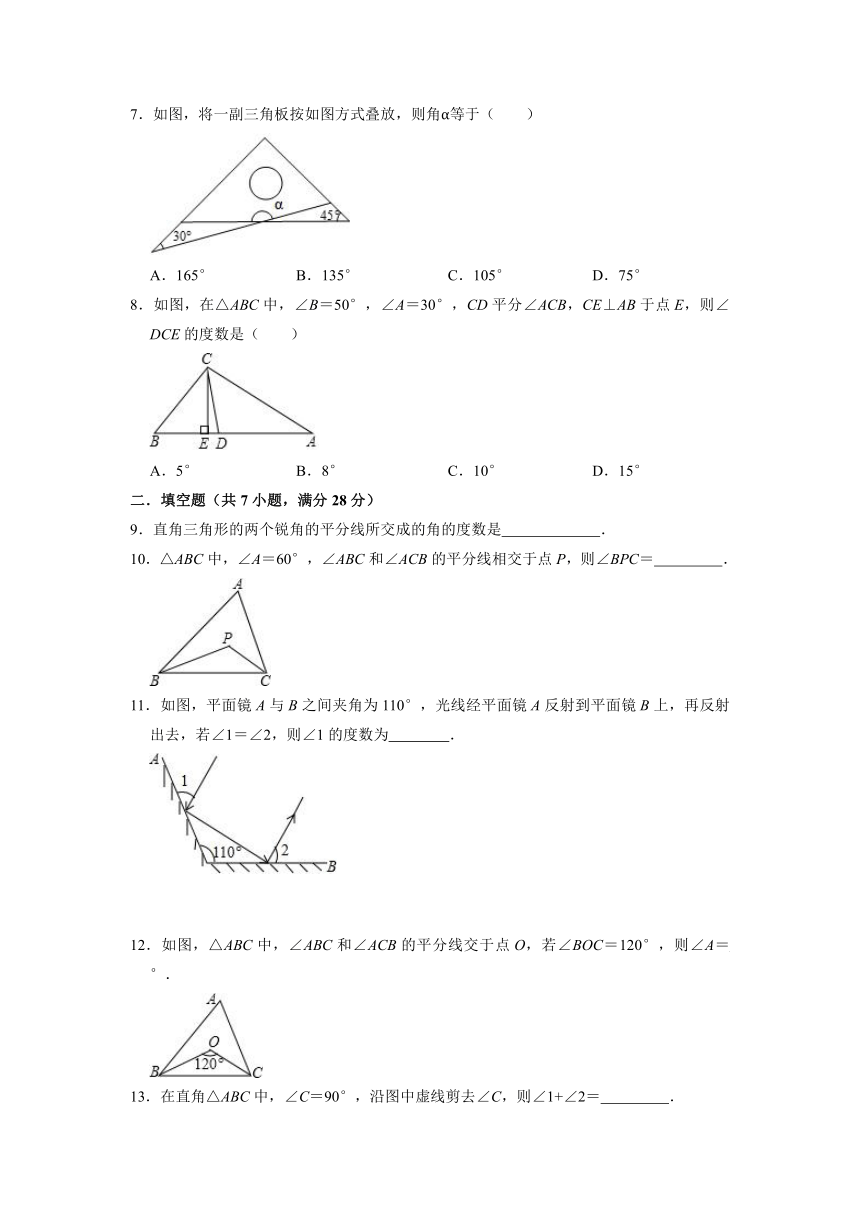
7.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
8.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5° B.8° C.10° D.15°
二.填空题(共7小题,满分28分)
9.直角三角形的两个锐角的平分线所交成的角的度数是 .
10.△ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC= .
11.如图,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若∠1=∠2,则∠1的度数为 .
12.如图,△ABC中,∠ABC和∠ACB的平分线交于点O,若∠BOC=120°,则∠A= °.
13.在直角△ABC中,∠C=90°,沿图中虚线剪去∠C,则∠1+∠2= .
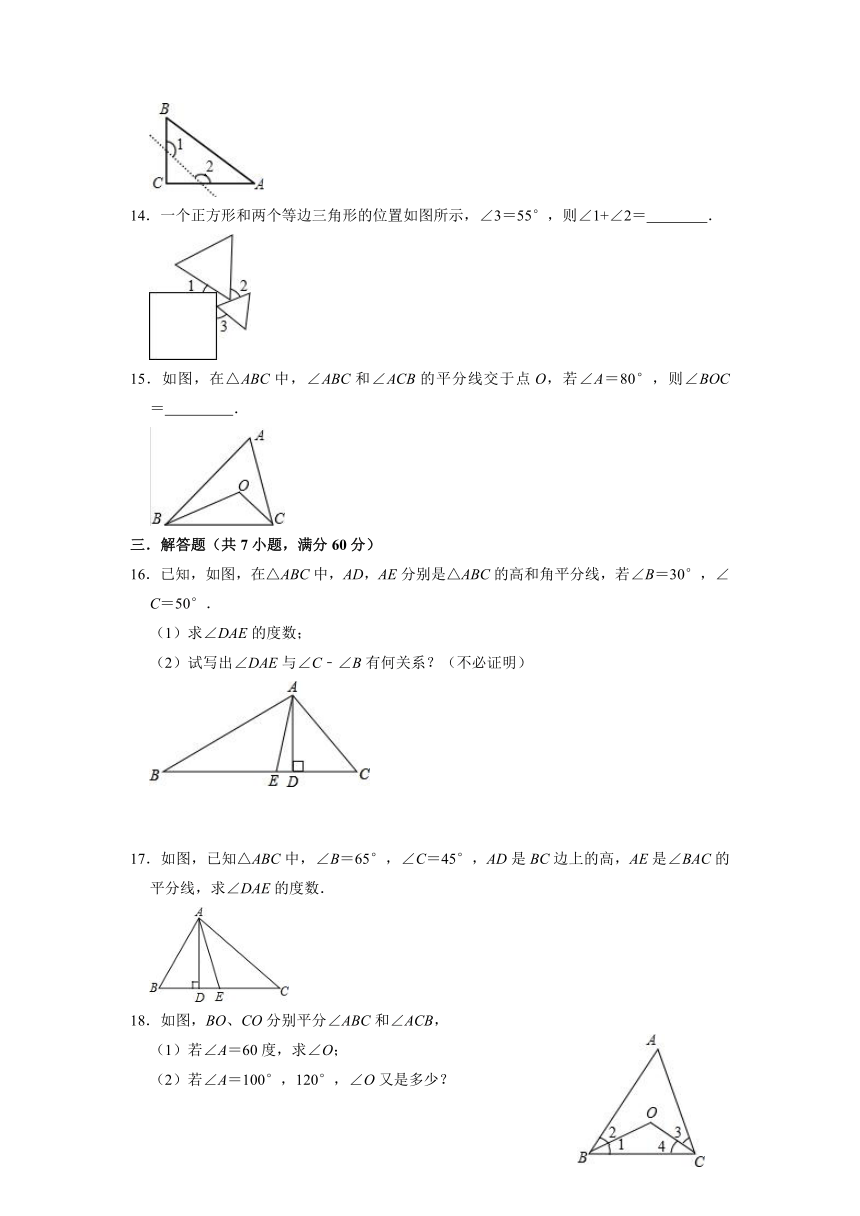
14.一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2= .
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC= .
三.解答题(共7小题,满分60分)
16.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C﹣∠B有何关系?(不必证明)
17.如图,已知△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
18.如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A=60度,求∠O;
(2)若∠A=100°,120°,∠O又是多少?
(3)由(1)、(2)你发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?(提示:三角形的内角和等于180°)
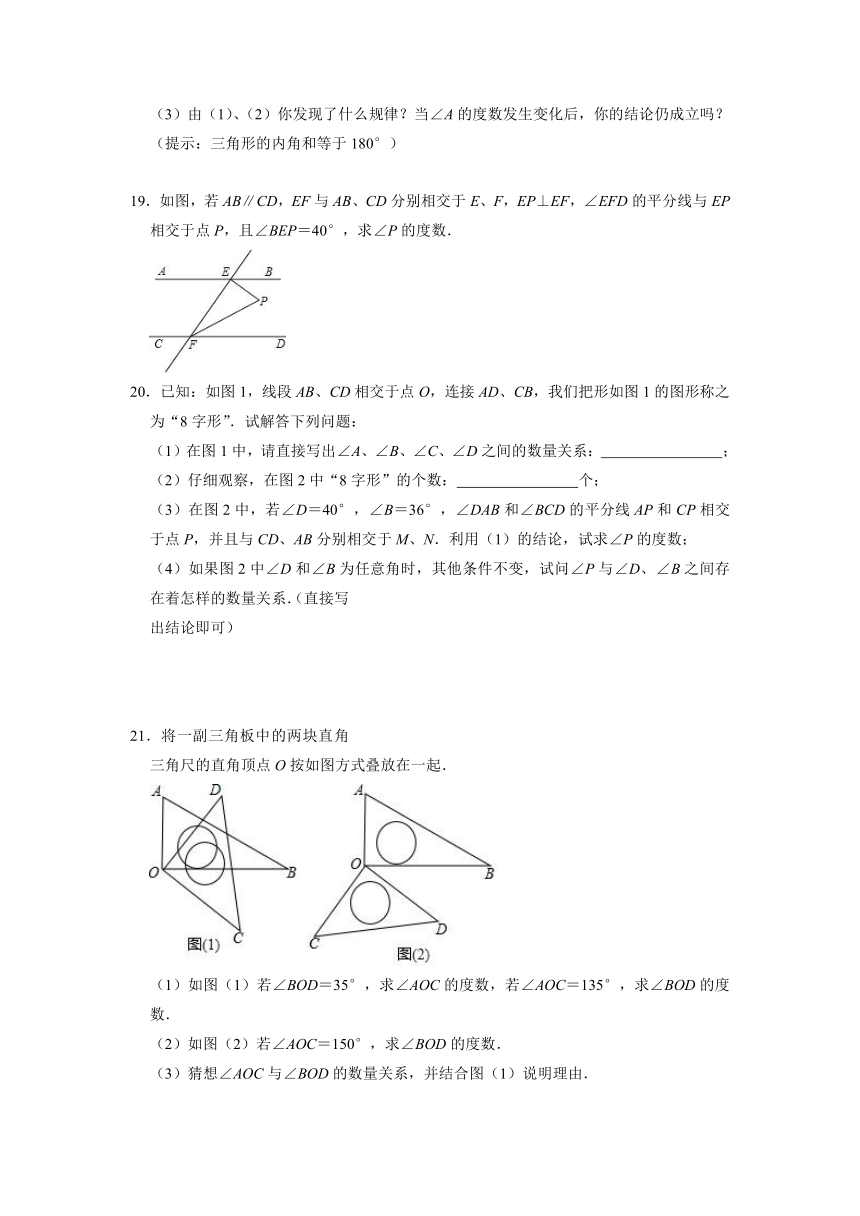
19.如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.
20.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
21.将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数.
(2)如图(2)若∠AOC=150°,求∠BOD的度数.
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
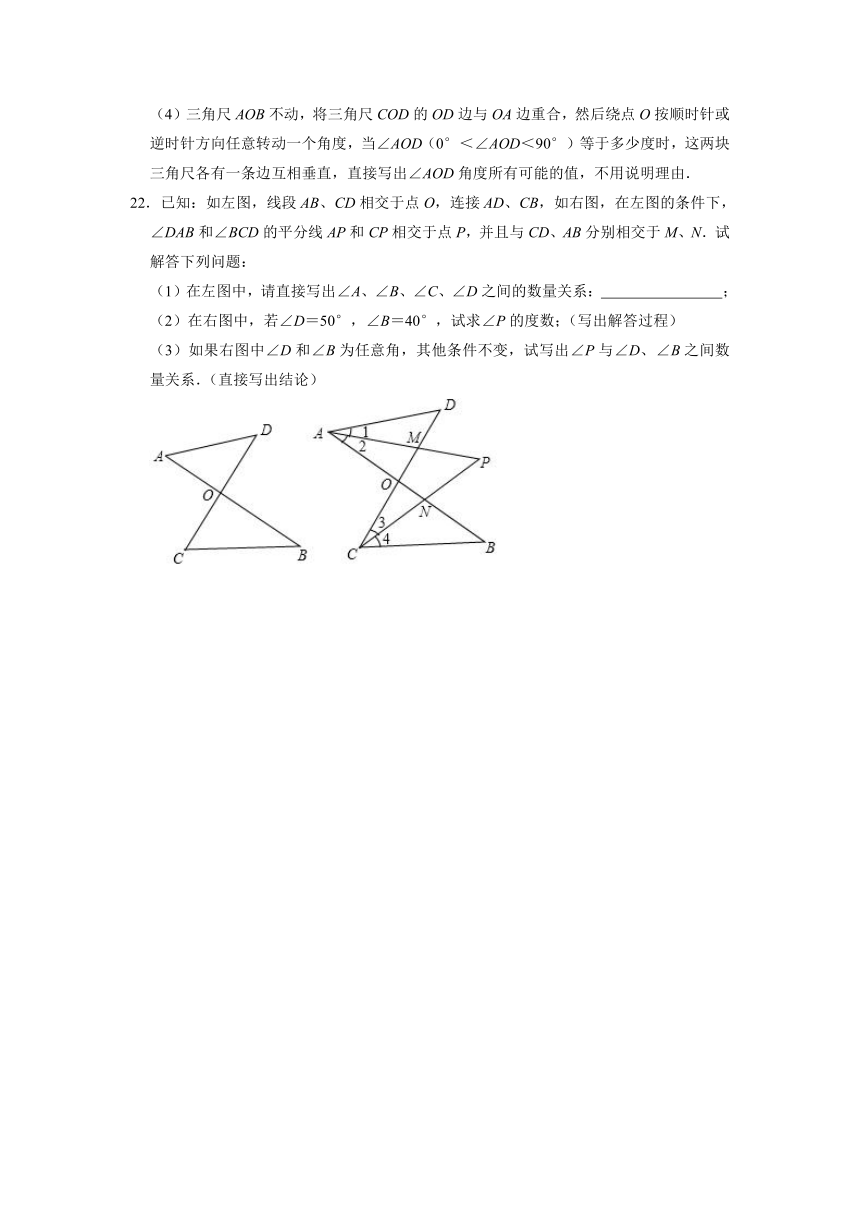
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
22.已知:如左图,线段AB、CD相交于点O,连接AD、CB,如右图,在左图的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在左图中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)在右图中,若∠D=50°,∠B=40°,试求∠P的度数;(写出解答过程)
(3)如果右图中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间数量关系.(直接写出结论)
参考答案
一.选择题(共8小题,满分32分)
1.解:设三个内角分别为2k、3k、4k,
则2k+3k+4k=180°,
解得k=20°,
所以,最大的角为4×20°=80°,
所以,三角形是锐角三角形.
故选:A.
2.解:∵∠1是△ABG的外角,
∴∠1=∠A+∠B,
∵∠2是△EFH的外角,
∴∠2=∠E+∠F,
∵∠3是△CDI的外角,
∴∠3=∠C+∠D,
∵∠1、∠2、∠3是△GIH的外角,
∴∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故选:B.
3.解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,即6∠A=180°,
∴∠A=30°,
∴∠B=60°,∠C=90°,
∴△ABC为直角三角形.
故选:B.
4.解:∴∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=130°﹣30°﹣40°=60°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=120°,
故选:B.
5.解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC=60°=30°,∠PCB=∠ACB=80°=40°.
由三角形的内角和定理可知:∠BPC=180°﹣∠PBC﹣∠PCB=180°﹣30°﹣40°=110°.
故选:B.
6.解:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则∠A=°,所以A选项错误;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,则∠C=60°,不能确定△ABC为直角三角形,所以B选项错误;
C、∠A+∠B+∠C=180°,而∠A=∠B=30°,则∠C=150°,所以B选项错误;
D、∠A+∠B+∠C=180°,而∠A=∠B=∠C,则∠C=90°,所以D选项正确.
故选:D.
7.解:∠1=90°﹣30°=60°,
∴∠2=∠1﹣45°=15°,
∴∠α=180°﹣15°=165°,
故选:A.
8.解:∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=∠BCA=×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选:C.
二.填空题(共7小题,满分28分)
9.解:直角三角形的两个锐角的平分线所交成的锐角是×90°=45°,
则直角三角形的两个锐角的平分线所交成的钝角是180°﹣45°=135°.
故答案为:45°或135°.
10.解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×120°=60°,
在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣60°=120°.
故答案为:120°.
11.解:由反射角等于入射角,可得:∠1=∠3,∠2=∠4,
∵∠1=∠2,
∴∠3=∠4,
∵∠AOB=110°,∠AOB+∠3+∠4=180°,
∴∠3+∠4=70°,
∴∠3=35°,
∴∠1=35°.
故答案为:35°.
12.解:如图,
∵∠BOC=120°,
∴∠1+∠4=180°﹣∠BOC=180°﹣120°=60°,
而∠ABC和∠ACB的平分线交于点O,
∴∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=2×60°=120°,
∴∠A=180°﹣(∠1+∠2+∠3+∠4)=180°﹣120°=60°.
故答案为60°.
13.解:∵∠A+∠B+∠C=180°,
∴∠A+∠B=180°﹣∠C=90°,
∵∠1+∠2+∠A+∠B=360°,
∴∠1+∠2=360°﹣90°=270°.
故答案是:270°.
14.解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,
∠ABC=180°﹣60°﹣∠3=120°﹣∠3,
∠ACB=180°﹣60°﹣∠2=120°﹣∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,
∴∠1+∠2=150°﹣∠3,
∵∠3=55°,
∴∠1+∠2=150°﹣55°=95°.
故答案为:95°.
15.解:∵在△ABC中,∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣50°=130°.
故答案为:130°.
三.解答题(共7小题,满分60分)
16.解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°﹣30°﹣50°=100°.
∵AE是∠BAC的平分线,
∴∠BAE=50°.
在Rt△ABD中,∠BAD=90°﹣∠B=60°,
∴∠DAE=∠BAD﹣∠BAE=60°﹣50=10°;
(2)∠C﹣∠B=2∠DAE.
17.解:在△ABC中,
∵∠BAC=180°﹣∠B﹣∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°﹣∠B=25°,
∴∠DAE=∠BAE﹣∠BAD=10°.
18.解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠1=∠2,∠3=∠4.
(1)∵∠A=60°,
∴∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,
∴∠O=180°﹣60°=120°.
(2)若∠A=100°,
∴∠1+∠2+∠3+∠4=80°,
∴∠1+∠4=40°,
∴∠O=140°.
若∠A=120°,
∴∠1+∠2+∠3+∠4=60°,
∴∠1+∠4=30°,
∴∠O=150°.
(3)规律是∠O=90°+0.5∠A,当∠A的度数发生变化后,结论仍成立.
19.解:∵EP⊥EF,
∴∠PEM=90°,∠PEF=90°.
∵∠BEP=40°,
∴∠BEM=∠PEM﹣∠BEP=90°﹣40°=50°.
∵AB∥CD,
∴∠BEM=∠EFD=50°.
∵FP平分∠EFD,
∴∠EFP=∠EFD=25°,
∴∠P=90°﹣25°=65°.
20.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)交点有点M、O、N,
以M为交点有1个,为△AMD与△CMP,
以O为交点有4个,为△AOD与△COB,△AOM与△CON,△AOM与△COB,△CON与△AOD,
以N为交点有1个,为△ANP与△CNB,
所以,“8字形”图形共有6个;
(3)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(4)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
21.解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
(2)如图2,若∠AOC=150°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣150°﹣90°﹣90°
=30°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
22.解:(1)∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C,
故答案为∠A+∠D=∠B+∠C.
(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1﹣∠3=∠P﹣∠D,∠2﹣∠4=∠B﹣∠P,
又∵AP、CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,
∴∠P﹣∠D=∠B﹣∠P,
即2∠P=∠B+∠D,
∴∠P=(50°+40°)÷2=45°.
(3)由(2)可知:2∠P=∠B+∠D.
同步达标测试(附答案)
一.选择题(共8小题,满分32分)
1.如果三角形的三个内角的度数比是2:3:4,则它是( )
A.锐角三角形 B.钝角三角形
C.直角三角形 D.钝角或直角三角形
2.如图,点A、B、C、D、E、F是平面上的6个点,则∠A+∠B+∠C+∠D+∠E+∠F的度数是( )
A.180° B.360° C.540° D.720°
3.适合条件∠A=∠B=∠C的△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形
4.如图,在△ABC中,∠A=50°,∠1=30°,∠2=40°,∠D的度数是( )
A.110° B.120° C.130° D.140°
5.如图,在△ABC中,∠ABC=60°,∠ACB=80°,BP平分∠ABC,CP平分∠ACB,则∠BPC的大小是( )
A.100° B.110° C.115° D.120°
6.下列条件中,能判定△ABC为直角三角形的是( )
A.∠A=2∠B=3∠C B.∠A+∠B=2∠C
C.∠A=∠B=30° D.∠A=∠B=∠C
7.如图,将一副三角板按如图方式叠放,则角α等于( )
A.165° B.135° C.105° D.75°
8.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5° B.8° C.10° D.15°
二.填空题(共7小题,满分28分)
9.直角三角形的两个锐角的平分线所交成的角的度数是 .
10.△ABC中,∠A=60°,∠ABC和∠ACB的平分线相交于点P,则∠BPC= .
11.如图,平面镜A与B之间夹角为110°,光线经平面镜A反射到平面镜B上,再反射出去,若∠1=∠2,则∠1的度数为 .
12.如图,△ABC中,∠ABC和∠ACB的平分线交于点O,若∠BOC=120°,则∠A= °.
13.在直角△ABC中,∠C=90°,沿图中虚线剪去∠C,则∠1+∠2= .
14.一个正方形和两个等边三角形的位置如图所示,∠3=55°,则∠1+∠2= .
15.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC= .
三.解答题(共7小题,满分60分)
16.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.
(1)求∠DAE的度数;
(2)试写出∠DAE与∠C﹣∠B有何关系?(不必证明)
17.如图,已知△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.
18.如图,BO、CO分别平分∠ABC和∠ACB,
(1)若∠A=60度,求∠O;
(2)若∠A=100°,120°,∠O又是多少?
(3)由(1)、(2)你发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?(提示:三角形的内角和等于180°)
19.如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.
20.已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.利用(1)的结论,试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结论即可)
21.将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,求∠AOC的度数,若∠AOC=135°,求∠BOD的度数.
(2)如图(2)若∠AOC=150°,求∠BOD的度数.
(3)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(4)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直,直接写出∠AOD角度所有可能的值,不用说明理由.
22.已知:如左图,线段AB、CD相交于点O,连接AD、CB,如右图,在左图的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在左图中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)在右图中,若∠D=50°,∠B=40°,试求∠P的度数;(写出解答过程)
(3)如果右图中∠D和∠B为任意角,其他条件不变,试写出∠P与∠D、∠B之间数量关系.(直接写出结论)
参考答案
一.选择题(共8小题,满分32分)
1.解:设三个内角分别为2k、3k、4k,
则2k+3k+4k=180°,
解得k=20°,
所以,最大的角为4×20°=80°,
所以,三角形是锐角三角形.
故选:A.
2.解:∵∠1是△ABG的外角,
∴∠1=∠A+∠B,
∵∠2是△EFH的外角,
∴∠2=∠E+∠F,
∵∠3是△CDI的外角,
∴∠3=∠C+∠D,
∵∠1、∠2、∠3是△GIH的外角,
∴∠1+∠2+∠3=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故选:B.
3.解:∵∠A=∠B=∠C,
∴∠B=2∠A,∠C=3∠A,
∵∠A+∠B+∠C=180°,即6∠A=180°,
∴∠A=30°,
∴∠B=60°,∠C=90°,
∴△ABC为直角三角形.
故选:B.
4.解:∴∠A=50°,
∴∠ABC+∠ACB=180°﹣50°=130°,
∴∠DBC+∠DCB=∠ABC+∠ACB﹣∠1﹣∠2=130°﹣30°﹣40°=60°,
∴∠BDC=180°﹣(∠DBC+∠DCB)=120°,
故选:B.
5.解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC=∠ABC=60°=30°,∠PCB=∠ACB=80°=40°.
由三角形的内角和定理可知:∠BPC=180°﹣∠PBC﹣∠PCB=180°﹣30°﹣40°=110°.
故选:B.
6.解:A、∠A+∠B+∠C=180°,而∠A=2∠B=3∠C,则∠A=°,所以A选项错误;
B、∠A+∠B+∠C=180°,而∠A+∠B=2∠C,则∠C=60°,不能确定△ABC为直角三角形,所以B选项错误;
C、∠A+∠B+∠C=180°,而∠A=∠B=30°,则∠C=150°,所以B选项错误;
D、∠A+∠B+∠C=180°,而∠A=∠B=∠C,则∠C=90°,所以D选项正确.
故选:D.
7.解:∠1=90°﹣30°=60°,
∴∠2=∠1﹣45°=15°,
∴∠α=180°﹣15°=165°,
故选:A.
8.解:∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=∠BCA=×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选:C.
二.填空题(共7小题,满分28分)
9.解:直角三角形的两个锐角的平分线所交成的锐角是×90°=45°,
则直角三角形的两个锐角的平分线所交成的钝角是180°﹣45°=135°.
故答案为:45°或135°.
10.解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣60°=120°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=(∠ABC+∠ACB)=×120°=60°,
在△PBC中,∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣60°=120°.
故答案为:120°.
11.解:由反射角等于入射角,可得:∠1=∠3,∠2=∠4,
∵∠1=∠2,
∴∠3=∠4,
∵∠AOB=110°,∠AOB+∠3+∠4=180°,
∴∠3+∠4=70°,
∴∠3=35°,
∴∠1=35°.
故答案为:35°.
12.解:如图,
∵∠BOC=120°,
∴∠1+∠4=180°﹣∠BOC=180°﹣120°=60°,
而∠ABC和∠ACB的平分线交于点O,
∴∠1=∠2,∠3=∠4,
∴∠1+∠2+∠3+∠4=2×60°=120°,
∴∠A=180°﹣(∠1+∠2+∠3+∠4)=180°﹣120°=60°.
故答案为60°.
13.解:∵∠A+∠B+∠C=180°,
∴∠A+∠B=180°﹣∠C=90°,
∵∠1+∠2+∠A+∠B=360°,
∴∠1+∠2=360°﹣90°=270°.
故答案是:270°.
14.解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,
∠ABC=180°﹣60°﹣∠3=120°﹣∠3,
∠ACB=180°﹣60°﹣∠2=120°﹣∠2,
在△ABC中,∠BAC+∠ABC+∠ACB=180°,
∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,
∴∠1+∠2=150°﹣∠3,
∵∠3=55°,
∴∠1+∠2=150°﹣55°=95°.
故答案为:95°.
15.解:∵在△ABC中,∠A=80°,
∴∠ABC+∠ACB=180°﹣80°=100°,
∵∠ABC和∠ACB的平分线交于O点,
∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣50°=130°.
故答案为:130°.
三.解答题(共7小题,满分60分)
16.解:(1)∵∠B=30°,∠C=50°,
∴∠BAC=180°﹣30°﹣50°=100°.
∵AE是∠BAC的平分线,
∴∠BAE=50°.
在Rt△ABD中,∠BAD=90°﹣∠B=60°,
∴∠DAE=∠BAD﹣∠BAE=60°﹣50=10°;
(2)∠C﹣∠B=2∠DAE.
17.解:在△ABC中,
∵∠BAC=180°﹣∠B﹣∠C=70°,
∵AE是∠BAC的平分线,
∴∠BAE=∠CAE=35°.
又∵AD是BC边上的高,
∴∠ADB=90°,
∵在△ABD中∠BAD=90°﹣∠B=25°,
∴∠DAE=∠BAE﹣∠BAD=10°.
18.解:∵BO、CO分别平分∠ABC和∠ACB,
∴∠1=∠2,∠3=∠4.
(1)∵∠A=60°,
∴∠1+∠2+∠3+∠4=120°,
∴∠1+∠4=60°,
∴∠O=180°﹣60°=120°.
(2)若∠A=100°,
∴∠1+∠2+∠3+∠4=80°,
∴∠1+∠4=40°,
∴∠O=140°.
若∠A=120°,
∴∠1+∠2+∠3+∠4=60°,
∴∠1+∠4=30°,
∴∠O=150°.
(3)规律是∠O=90°+0.5∠A,当∠A的度数发生变化后,结论仍成立.
19.解:∵EP⊥EF,
∴∠PEM=90°,∠PEF=90°.
∵∠BEP=40°,
∴∠BEM=∠PEM﹣∠BEP=90°﹣40°=50°.
∵AB∥CD,
∴∠BEM=∠EFD=50°.
∵FP平分∠EFD,
∴∠EFP=∠EFD=25°,
∴∠P=90°﹣25°=65°.
20.解:(1)在△AOD中,∠AOD=180°﹣∠A﹣∠D,
在△BOC中,∠BOC=180°﹣∠B﹣∠C,
∵∠AOD=∠BOC(对顶角相等),
∴180°﹣∠A﹣∠D=180°﹣∠B﹣∠C,
∴∠A+∠D=∠B+∠C;
(2)交点有点M、O、N,
以M为交点有1个,为△AMD与△CMP,
以O为交点有4个,为△AOD与△COB,△AOM与△CON,△AOM与△COB,△CON与△AOD,
以N为交点有1个,为△ANP与△CNB,
所以,“8字形”图形共有6个;
(3)∵∠D=40°,∠B=36°,
∴∠OAD+40°=∠OCB+36°,
∴∠OCB﹣∠OAD=4°,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
又∵∠DAM+∠D=∠PCM+∠P,
∴∠P=∠DAM+∠D﹣∠PCM=(∠OAD﹣∠OCB)+∠D=×(﹣4°)+40°=38°;
(4)根据“8字形”数量关系,∠OAD+∠D=∠OCB+∠B,∠DAM+∠D=∠PCM+∠P,
所以,∠OCB﹣∠OAD=∠D﹣∠B,∠PCM﹣∠DAM=∠D﹣∠P,
∵AP、CP分别是∠DAB和∠BCD的角平分线,
∴∠DAM=∠OAD,∠PCM=∠OCB,
∴(∠D﹣∠B)=∠D﹣∠P,
整理得,2∠P=∠B+∠D.
21.解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD﹣∠BOD=90°+90°﹣35°=145°,
若∠AOC=135°,
则∠BOD=∠AOB+∠COD﹣∠AOC=90°+90°﹣135°=45°;
(2)如图2,若∠AOC=150°,
则∠BOD=360°﹣∠AOC﹣∠AOB﹣∠COD
=360°﹣150°﹣90°﹣90°
=30°;
(3)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
(4)OD⊥AB时,∠AOD=30°,
CD⊥OB时,∠AOD=45°,
CD⊥AB时,∠AOD=75°,
OC⊥AB时,∠AOD=60°,
即∠AOD角度所有可能的值为:30°、45°、60°、75°.
22.解:(1)∵∠A+∠D+∠AOD=∠B+∠C+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C,
故答案为∠A+∠D=∠B+∠C.
(2)由(1)得,∠1+∠D=∠3+∠P,∠2+∠P=∠4+∠B,
∴∠1﹣∠3=∠P﹣∠D,∠2﹣∠4=∠B﹣∠P,
又∵AP、CP分别平分∠DAB和∠BCD,
∴∠1=∠2,∠3=∠4,
∴∠P﹣∠D=∠B﹣∠P,
即2∠P=∠B+∠D,
∴∠P=(50°+40°)÷2=45°.
(3)由(2)可知:2∠P=∠B+∠D.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
