2021-2022学年北师大版七年级数学上册第6章数据的收集与整理章末知识点分类练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版七年级数学上册第6章数据的收集与整理章末知识点分类练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 163.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 00:00:00 | ||
图片预览



文档简介
2021-2022学年北师大版七年级数学上册《第6章数据的收集与整理》
章末知识点分类练习(附答案)
一.调查收集数据的过程与方法
1.某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如表尚不完整的调查问卷:
调查问卷□______年______月______日你平时最喜欢的一种体育运动项目是( )(单选)A.B.C.D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是( )
A.①②③ B.①③⑤ C.②③④ D.②④⑤
2.小李在家门口进行了一项社会调查,对从家门口经过的车辆进行记录,分析出本地车与外地车辆的数据,同时也对汽车牌照的尾号进行记录.
(1)在这过程中他要收集哪些数据?
(2)设计出记录用的表格.
二.全面调查与抽样调查
3.下列调查适合做抽样调查的是( )
A.对某小区的卫生死角进行调查
B.对中学生目前的睡眠情况进行调查
C.对八名同学的身高情况进行调查
D.审核书稿中的错别字
4.下列调查中,适合用全面调查方式的是( )
A.了解某校七年级学生期末数学考试的成绩
B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况
D.了解春节联欢晚会的收视率
5.小龙的妈妈让小龙去买一盒火柴,并叮嘱小龙,一定要试试火柴是否好用.小龙回家后,高兴地告诉妈妈:“火柴好用,我每根都试过了.”
(1)小龙采取的方法是哪种调查?
(2)你认为小龙采取的方法是否合适?为什么?
6.琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么?
(2)调查的范围有多大?用了哪种调查方式?
三.总体、个体、样本、样本容量
7.为了解某校七年级800名学生防诈骗的安全意识,王老师从中抽了40名学生进行了问卷调查,其中的40是( )
A.总体 B.个体 C.样本容量 D.样本
四.抽样调查的可靠性
8.为调查某大学新生对学校的满意程度,以下抽样调查最合适的是( )
A.学校新生中的男生 B.学校全体学生
C.学校新生中的女生 D.用新生名单,随机抽取三分之一的新生
9.下列的调查中,选取的样本最具有代表性的是( )
A.为了解九龙坡区居民的防火意识,对该地区的初中生进行调查
B.为了解万象城某专卖店的平均营业额,选在周末进行调查
C.为了解某校1500名学生的视力情况,随机抽取该校150名学生进行调查
D.为了解全校学生课外小组的活动情况,对该校的女生进行调查
五.用样本估计总体
10.某农户在山上种了脐橙果树44株,现进入第三年收获期,收获时,先随意采摘5株果树上的脐橙,称得每株树上的脐橙重量如下(单位:千克):35,35,34,39,37.若市场上的脐橙售价为每千克5元,估计这年该农户卖脐橙的收入为 元.
11.今年世界环境日(即6月5日),某市发布了一份空气质量的抽样调查报告,其中该市2~5月随机调查的25天各空气质量级别的天数如下表所示:
空气污染指数 0~50 51~100 101~150 151~200 201~250
空气质量级别 优 良 轻微污染 轻度污染 中度污染
天 数 8 12 2 2 1
(1)试估计该市今年的空气质量主要是哪个级别?
(2)根据抽样数据,预测该市今年空气质量级别为优和良的天数共约为多少天?
(3)根据调查报告,试对有关部门提一条建设“绿色城市”的建议.
12.许多高校均投放了使用手机就可使用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费做如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 0 1 2 3 4 5(含5次以上)
累计车费 0 0.5 0.9 a b 1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 0 1 2 3 4 5
人数 5 15 10 30 25 15
(1)写出a,b的值;
(2)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
六.频数与频率
13.“新冠病毒”的英语“Novelcoronavirus”中,字母“n”出现的频率是( )
A. B. C.2 D.1
14.小丽抛一枚硬币10次,其中有6次正面朝上,则反面朝上的频数是( )
A.6 B.0.6 C.4 D.0.4
七.频数(率)分布表
15.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
八.频数(率)分布直方图
16.为了了解某中学男学生的身高情况,随机抽取50名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).则抽取的男生中身高在169.5cm~174.5cm之间的人数是( )
A.12 B.18 C.20 D.24
17.某地七年级有3000名学生参加网上“爱我中华知识竞赛”活动.为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 0.08
70≤x<80 b 0.20
80≤x<90 62 c
90≤x<100 72 0.36
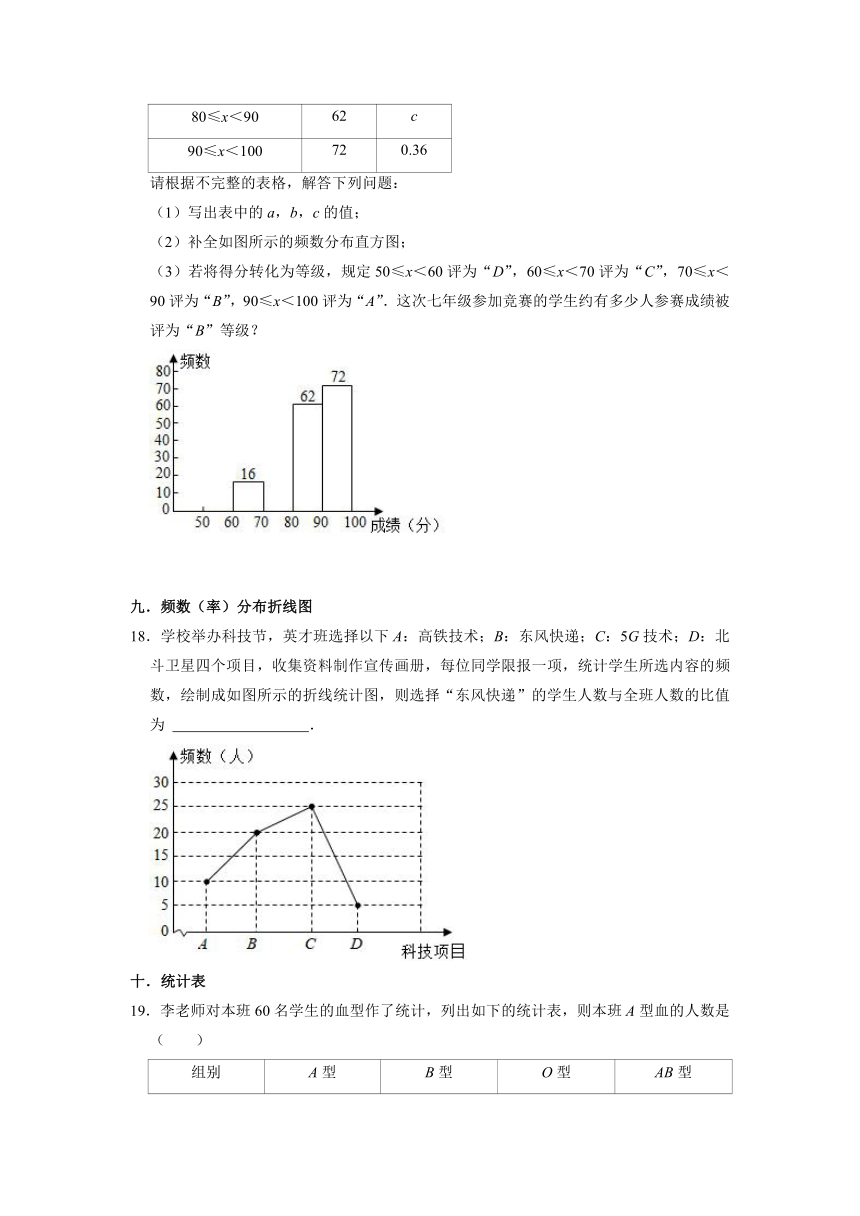
请根据不完整的表格,解答下列问题:
(1)写出表中的a,b,c的值;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次七年级参加竞赛的学生约有多少人参赛成绩被评为“B”等级?
九.频数(率)分布折线图
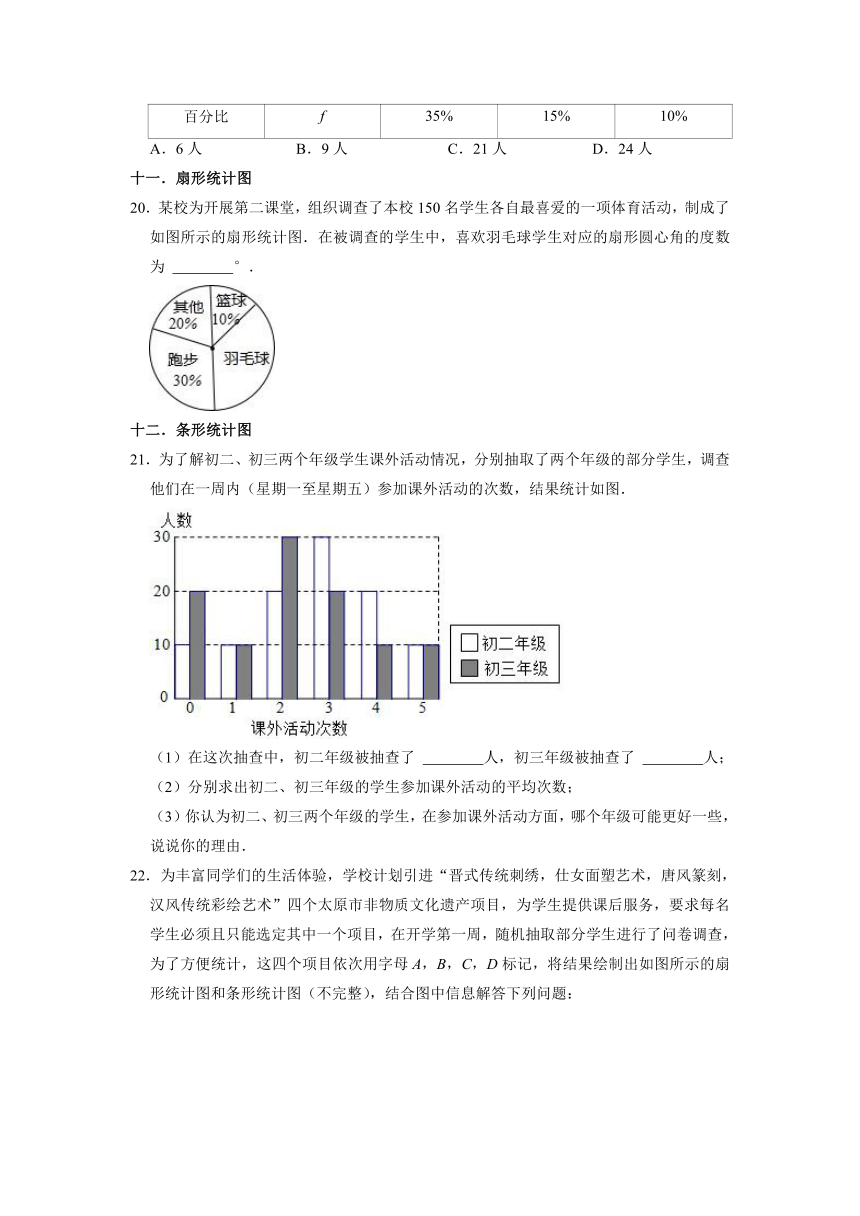
18.学校举办科技节,英才班选择以下A:高铁技术;B:东风快递;C:5G技术;D:北斗卫星四个项目,收集资料制作宣传画册,每位同学限报一项,统计学生所选内容的频数,绘制成如图所示的折线统计图,则选择“东风快递”的学生人数与全班人数的比值为 .
十.统计表
19.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
十一.扇形统计图
20.某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如图所示的扇形统计图.在被调查的学生中,喜欢羽毛球学生对应的扇形圆心角的度数为 °.
十二.条形统计图
21.为了解初二、初三两个年级学生课外活动情况,分别抽取了两个年级的部分学生,调查他们在一周内(星期一至星期五)参加课外活动的次数,结果统计如图.
(1)在这次抽查中,初二年级被抽查了 人,初三年级被抽查了 人;
(2)分别求出初二、初三年级的学生参加课外活动的平均次数;
(3)你认为初二、初三两个年级的学生,在参加课外活动方面,哪个年级可能更好一些,说说你的理由.
22.为丰富同学们的生活体验,学校计划引进“晋式传统刺绣,仕女面塑艺术,唐风篆刻,汉风传统彩绘艺术”四个太原市非物质文化遗产项目,为学生提供课后服务,要求每名学生必须且只能选定其中一个项目,在开学第一周,随机抽取部分学生进行了问卷调查,为了方便统计,这四个项目依次用字母A,B,C,D标记,将结果绘制出如图所示的扇形统计图和条形统计图(不完整),结合图中信息解答下列问题:
(1)被调查的学生共有 人;在扇形统计图中,B所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)已知该校有1600学生,请估计选定“汉风传统彩绘艺术”项目的人数.
十三.折线统计图
23.某校积极开展劳动教育,决定成立种植玉米、种植大豆、种植西红柿三个小组,每名学生最多选择一个小组.为了解学生的选择意向,随机抽取七年级(1)(2)(3)(4)四个班共200名学生进行调查,将调查得到的数据进行整理,绘制成如图所示两幅不完整的统计图,根据统计图提供的信息解答下列问题:
(1)求扇形统计图中,种植西红柿所占的百分比;
(2)求(4)班选择种植大豆小组的学生人数,补全折线统计图;
(3)若该校共有2500人,请你估计该校学生选择种植玉米小组的人数.
十四.统计图的选择
24.近年来,我国城乡居民的收入有了大幅提高,为了了解我国城乡居民收入10年来的变化趋势,适合采用的统计图是 .(填“扇形统计图”或“折线统计图”)
参考答案
一.调查收集数据的过程与方法
1.解:由于调查问卷的设置选项的“不重复、不包含、各个选项相互独立”可得,②③④符合题意,
故选:C.
2.解:(1)收集两种数据:本地车与外地车数据;汽车尾号数据.
(2)记录用的表格如下:
上午 下午 车牌尾号
外地
本地
二.全面调查与抽样调查
3.解:A.对某小区的卫生死角进行调查,适合做全面调查,故本选项不合题意;
B.对中学生目前的睡眠情况进行调查,适合做抽样调查,故本选项符合题意;
C.对八名同学的身高情况进行调查,适合做全面调查,故本选项不合题意;
D.审核书稿中的错别字,适合做全面调查,故本选项不合题意
故选:B.
4.解:A.了解某校七年级学生期末数学考试的成绩,适合采用普查方式,故本选项符合题意;
B.了解一批签字笔的使用寿命,由于调查具有破坏性,适合采用抽样调查,故本选项不合题意;
C.了解市场上酸奶的质量情况,由于调查具有破坏性,适合采用抽样调查,故本选项不合题意;
D.了解春节联欢晚会的收视率,由于工作量大,适合采用抽样调查,故本选项不合题意.
故选:A.
5.解:(1)小龙采取的是全面调查;
(2)小龙采取的方法不合适,因为具有破坏性,所以应用抽样调查.
6.解:(1)调查的问题是全市八年级学生每天写作业的时间;
(2)调查的范围是某校八年级(4)班全体学生,用了抽样调查方式.
三.总体、个体、样本、样本容量
7.解:为了解某校七年级800名学生防诈骗的安全意识,王老师从中抽了40名学生进行了问卷调查,其中的40是样本容量.
故选:C.
四.抽样调查的可靠性
8.解:A.学校新生中的男生,样本不具有代表性,故不符合题意;
B.学校全体学生,样本不具有代表性,故不符合题意;
C.学校新生中的女生,样本不具有代表性,故不符合题意;
D.用新生名单,随机抽取三分之一的新生,样本具有代表性,故符合题意;
故选:D.
9.解:A.为了解九龙坡区居民的防火意识,对该地区的初中生进行调查,不具有代表性,故A选项不符合题意;
B.为了解万象城某专卖店的平均营业额,选在周末进行调查,不具有代表性,故B选项不符合题意;
C.为了解某校1500名学生的视力情况,随机抽取该校150名学生进行调查,具有代表性,故C选项符合题意;
D.为了解全校学生课外小组的活动情况,对该校的女生进行调查,不具有代表性,故D选项不符合题意;
故选:C.
五.用样本估计总体
10.解:该农户卖脐橙的收入为:(35+35+34+39+37)÷5×44×5=7920(元).
故答案为:7920.
11.解:(1)根据表格可得该市今年的空气质量主要是良;
(2)该市今年空气质量级别为优和良的天数:×365=292(天);
(3)减少废气的排放;多植树;对垃圾及时的进行处理并且可回收的垃圾与不可回收的垃圾分开.
12.解:(1)a=0.9+0.3=1.2,b=1.2+0.2=1.4;
(2)根据用车意愿调查结果,抽取的100名师生每人每天使用A品牌共享单车的平均车费为:
×(0×5+0.5×15+0.9×10+1.2×30+1.4×25+1.5×15)=1.1(元),
所以估计5000名师生一天使用共享单车的费用为:5000×1.1=5500(元),
因为5500<5800,
故收费调整后,此运营商在该校投放A品牌共享单车不能获利.
六.频数与频率
13.解:在“Novelcoronavirus”中,字母的总数是16,字母“n”有2个,
因而字母“n”出现的频率是:=.
故选:B.
14.解:小丽抛一枚硬币10次,6次正面朝上,4次反面朝上,则正面朝上的频数是6,反面朝上的频数是4.
故选:C.
七.频数(率)分布表
15.解:∵数据的最大值是132,最小值是89,
∴极差为132﹣89=43,
又∵组距为5,
∴43÷5=8.6,
∴组数为9,
故选:C.
八.频数(率)分布直方图
16.解:由直方图可得,
抽取的男生中身高在169.5cm~174.5cm之间的男生有:50﹣6﹣10﹣16﹣6=12(人),
故选:A.
17.解:(1)a=10÷200=0.05,b=200×0.20=40,c=62÷200=0.31,
即a,b,c的值分别为0.05,40,0.31;
(2)由频数分布表可知,50≤x<60对应的频数为10,
由(1)知b=40,
补全的频数分布直方图如右图所示;
(3)3000×(0.20+0.31)
=3000×0.51
=1530(人),
答:这次七年级参加竞赛的学生约有1530人参赛成绩被评为“B”等级.
九.频数(率)分布折线图
18.解:由图知,英才班的全体人数为:10+20+25+5=60(人),
选择“东风快递”的学生人数为:20人,
∴选择“东风快递”的学生人数与全班人数的比值为:=.
故答案为:.
十.统计表
19.解:60×(1﹣35%﹣15%﹣10%)=24(人),
故选:D.
十一.扇形统计图
20.解:360°×(1﹣10%﹣20%﹣30%)=144°,
故答案为:144.
十二.条形统计图
21.解:(1)由统计图可得,
初二年级被抽查了:10+10+20+30+20+10=100(人),
初三年级被抽查了:20+10+30+20+10+10=100(人),
故答案为:100,100;
初二年级的学生参加课外活动的平均次数是
=2.7(次),
初三年级的学生参加课外活动的平均次数是:
=2.2(次),
即初二、初三年级的学生参加课外活动的平均次数分别为2.7次,2.2次;
(3)初二在参加课外活动方面,可能更好一些.
理由:初二学生不用面临毕业考试,学习压力不算大,可以有较多的时间参加课外活动,而初三的学生面临升学考试,学习压力大,相对参加课外活动的时间就少一些.
22.解:(1)被调查的学生共有:20÷20%=100(人);
在扇形统计图中,D所占的百分比为:×100%=35%,
故B所对应的圆心角的度数为:360°×(1﹣20%﹣30%﹣35%)=54°.
故答案为:100;54°.
(2)B的人数为:100×15%=15(人),C的人数为:100×30%=30(人),
补充完整如图所示:
(3)该校选定“汉风传统彩绘艺术”项目的人数大约有:1600×35%=560(人).
十三.折线统计图
23.解:(1)(12+15+13+14)÷200×100%=27%.
所以种植西红柿所占的百分比为27%;
(2)30%×200=60(人),
60﹣15﹣14﹣16=15(人).
答:(4)班选择种植大豆小组的学生人数为15人,
(3)2500×(1﹣30%﹣5%﹣27%)
=950(人).
答:估计该校学生选择种植玉米小组的人数为950人.
十四.统计图的选择
24.解:由于需要了解我国城乡居民收入10年来的变化趋势,所以适合采用的统计图是折线统计图,
故答案为:折线统计图.
章末知识点分类练习(附答案)
一.调查收集数据的过程与方法
1.某班级组织活动,为了解同学们喜爱的体育运动项目,设计了如表尚不完整的调查问卷:
调查问卷□______年______月______日你平时最喜欢的一种体育运动项目是( )(单选)A.B.C.D.其他运动项目
准备在“①室外体育运动,②篮球,③足球,④游泳,⑤球类运动”中选取三个作为该调查问卷问题的备选项目,选取合理的是( )
A.①②③ B.①③⑤ C.②③④ D.②④⑤
2.小李在家门口进行了一项社会调查,对从家门口经过的车辆进行记录,分析出本地车与外地车辆的数据,同时也对汽车牌照的尾号进行记录.
(1)在这过程中他要收集哪些数据?
(2)设计出记录用的表格.
二.全面调查与抽样调查
3.下列调查适合做抽样调查的是( )
A.对某小区的卫生死角进行调查
B.对中学生目前的睡眠情况进行调查
C.对八名同学的身高情况进行调查
D.审核书稿中的错别字
4.下列调查中,适合用全面调查方式的是( )
A.了解某校七年级学生期末数学考试的成绩
B.了解一批签字笔的使用寿命
C.了解市场上酸奶的质量情况
D.了解春节联欢晚会的收视率
5.小龙的妈妈让小龙去买一盒火柴,并叮嘱小龙,一定要试试火柴是否好用.小龙回家后,高兴地告诉妈妈:“火柴好用,我每根都试过了.”
(1)小龙采取的方法是哪种调查?
(2)你认为小龙采取的方法是否合适?为什么?
6.琪琪想了解全市八年级学生每天写作业的时间,她对某校八年级(4)班全体学生每天写作业的时间进行了一次调查.
(1)调查的问题是什么?
(2)调查的范围有多大?用了哪种调查方式?
三.总体、个体、样本、样本容量
7.为了解某校七年级800名学生防诈骗的安全意识,王老师从中抽了40名学生进行了问卷调查,其中的40是( )
A.总体 B.个体 C.样本容量 D.样本
四.抽样调查的可靠性
8.为调查某大学新生对学校的满意程度,以下抽样调查最合适的是( )
A.学校新生中的男生 B.学校全体学生
C.学校新生中的女生 D.用新生名单,随机抽取三分之一的新生
9.下列的调查中,选取的样本最具有代表性的是( )
A.为了解九龙坡区居民的防火意识,对该地区的初中生进行调查
B.为了解万象城某专卖店的平均营业额,选在周末进行调查
C.为了解某校1500名学生的视力情况,随机抽取该校150名学生进行调查
D.为了解全校学生课外小组的活动情况,对该校的女生进行调查
五.用样本估计总体
10.某农户在山上种了脐橙果树44株,现进入第三年收获期,收获时,先随意采摘5株果树上的脐橙,称得每株树上的脐橙重量如下(单位:千克):35,35,34,39,37.若市场上的脐橙售价为每千克5元,估计这年该农户卖脐橙的收入为 元.
11.今年世界环境日(即6月5日),某市发布了一份空气质量的抽样调查报告,其中该市2~5月随机调查的25天各空气质量级别的天数如下表所示:
空气污染指数 0~50 51~100 101~150 151~200 201~250
空气质量级别 优 良 轻微污染 轻度污染 中度污染
天 数 8 12 2 2 1
(1)试估计该市今年的空气质量主要是哪个级别?
(2)根据抽样数据,预测该市今年空气质量级别为优和良的天数共约为多少天?
(3)根据调查报告,试对有关部门提一条建设“绿色城市”的建议.
12.许多高校均投放了使用手机就可使用的共享单车.某运营商为提高其经营的A品牌共享单车的市场占有率,准备对收费做如下调整:一天中,同一个人第一次使用的车费按0.5元收取,每增加一次,当次车费就比上次车费减少0.1元,第6次开始,当次用车免费.具体收费标准如下:
使用次数 0 1 2 3 4 5(含5次以上)
累计车费 0 0.5 0.9 a b 1.5
同时,就此收费方案随机调查了某高校100名师生在一天中使用A品牌共享单车的意愿,得到如下数据:
使用次数 0 1 2 3 4 5
人数 5 15 10 30 25 15
(1)写出a,b的值;
(2)已知该校有5000名师生,且A品牌共享单车投放该校一天的费用为5800元.试估计:收费调整后,此运营商在该校投放A品牌共享单车能否获利?说明理由.
六.频数与频率
13.“新冠病毒”的英语“Novelcoronavirus”中,字母“n”出现的频率是( )
A. B. C.2 D.1
14.小丽抛一枚硬币10次,其中有6次正面朝上,则反面朝上的频数是( )
A.6 B.0.6 C.4 D.0.4
七.频数(率)分布表
15.一组数据的最大值是132,最小值是89,将这组数据进行分组时,取组距为5,则组数是( )
A.7 B.8 C.9 D.10
八.频数(率)分布直方图
16.为了了解某中学男学生的身高情况,随机抽取50名男生进行身高测量,将所得数据整理后,画出频数分布直方图(如图).则抽取的男生中身高在169.5cm~174.5cm之间的人数是( )
A.12 B.18 C.20 D.24
17.某地七年级有3000名学生参加网上“爱我中华知识竞赛”活动.为了解本次知识竞赛成绩的分布情况,从中抽取了200名学生的得分进行统计.
成绩x(分) 频数 频率
50≤x<60 10 a
60≤x<70 16 0.08
70≤x<80 b 0.20
80≤x<90 62 c
90≤x<100 72 0.36
请根据不完整的表格,解答下列问题:
(1)写出表中的a,b,c的值;
(2)补全如图所示的频数分布直方图;
(3)若将得分转化为等级,规定50≤x<60评为“D”,60≤x<70评为“C”,70≤x<90评为“B”,90≤x<100评为“A”.这次七年级参加竞赛的学生约有多少人参赛成绩被评为“B”等级?
九.频数(率)分布折线图
18.学校举办科技节,英才班选择以下A:高铁技术;B:东风快递;C:5G技术;D:北斗卫星四个项目,收集资料制作宣传画册,每位同学限报一项,统计学生所选内容的频数,绘制成如图所示的折线统计图,则选择“东风快递”的学生人数与全班人数的比值为 .
十.统计表
19.李老师对本班60名学生的血型作了统计,列出如下的统计表,则本班A型血的人数是( )
组别 A型 B型 O型 AB型
百分比 f 35% 15% 10%
A.6人 B.9人 C.21人 D.24人
十一.扇形统计图
20.某校为开展第二课堂,组织调查了本校150名学生各自最喜爱的一项体育活动,制成了如图所示的扇形统计图.在被调查的学生中,喜欢羽毛球学生对应的扇形圆心角的度数为 °.
十二.条形统计图
21.为了解初二、初三两个年级学生课外活动情况,分别抽取了两个年级的部分学生,调查他们在一周内(星期一至星期五)参加课外活动的次数,结果统计如图.
(1)在这次抽查中,初二年级被抽查了 人,初三年级被抽查了 人;
(2)分别求出初二、初三年级的学生参加课外活动的平均次数;
(3)你认为初二、初三两个年级的学生,在参加课外活动方面,哪个年级可能更好一些,说说你的理由.
22.为丰富同学们的生活体验,学校计划引进“晋式传统刺绣,仕女面塑艺术,唐风篆刻,汉风传统彩绘艺术”四个太原市非物质文化遗产项目,为学生提供课后服务,要求每名学生必须且只能选定其中一个项目,在开学第一周,随机抽取部分学生进行了问卷调查,为了方便统计,这四个项目依次用字母A,B,C,D标记,将结果绘制出如图所示的扇形统计图和条形统计图(不完整),结合图中信息解答下列问题:
(1)被调查的学生共有 人;在扇形统计图中,B所对应的圆心角的度数为 ;
(2)补全条形统计图;
(3)已知该校有1600学生,请估计选定“汉风传统彩绘艺术”项目的人数.
十三.折线统计图
23.某校积极开展劳动教育,决定成立种植玉米、种植大豆、种植西红柿三个小组,每名学生最多选择一个小组.为了解学生的选择意向,随机抽取七年级(1)(2)(3)(4)四个班共200名学生进行调查,将调查得到的数据进行整理,绘制成如图所示两幅不完整的统计图,根据统计图提供的信息解答下列问题:
(1)求扇形统计图中,种植西红柿所占的百分比;
(2)求(4)班选择种植大豆小组的学生人数,补全折线统计图;
(3)若该校共有2500人,请你估计该校学生选择种植玉米小组的人数.
十四.统计图的选择
24.近年来,我国城乡居民的收入有了大幅提高,为了了解我国城乡居民收入10年来的变化趋势,适合采用的统计图是 .(填“扇形统计图”或“折线统计图”)
参考答案
一.调查收集数据的过程与方法
1.解:由于调查问卷的设置选项的“不重复、不包含、各个选项相互独立”可得,②③④符合题意,
故选:C.
2.解:(1)收集两种数据:本地车与外地车数据;汽车尾号数据.
(2)记录用的表格如下:
上午 下午 车牌尾号
外地
本地
二.全面调查与抽样调查
3.解:A.对某小区的卫生死角进行调查,适合做全面调查,故本选项不合题意;
B.对中学生目前的睡眠情况进行调查,适合做抽样调查,故本选项符合题意;
C.对八名同学的身高情况进行调查,适合做全面调查,故本选项不合题意;
D.审核书稿中的错别字,适合做全面调查,故本选项不合题意
故选:B.
4.解:A.了解某校七年级学生期末数学考试的成绩,适合采用普查方式,故本选项符合题意;
B.了解一批签字笔的使用寿命,由于调查具有破坏性,适合采用抽样调查,故本选项不合题意;
C.了解市场上酸奶的质量情况,由于调查具有破坏性,适合采用抽样调查,故本选项不合题意;
D.了解春节联欢晚会的收视率,由于工作量大,适合采用抽样调查,故本选项不合题意.
故选:A.
5.解:(1)小龙采取的是全面调查;
(2)小龙采取的方法不合适,因为具有破坏性,所以应用抽样调查.
6.解:(1)调查的问题是全市八年级学生每天写作业的时间;
(2)调查的范围是某校八年级(4)班全体学生,用了抽样调查方式.
三.总体、个体、样本、样本容量
7.解:为了解某校七年级800名学生防诈骗的安全意识,王老师从中抽了40名学生进行了问卷调查,其中的40是样本容量.
故选:C.
四.抽样调查的可靠性
8.解:A.学校新生中的男生,样本不具有代表性,故不符合题意;
B.学校全体学生,样本不具有代表性,故不符合题意;
C.学校新生中的女生,样本不具有代表性,故不符合题意;
D.用新生名单,随机抽取三分之一的新生,样本具有代表性,故符合题意;
故选:D.
9.解:A.为了解九龙坡区居民的防火意识,对该地区的初中生进行调查,不具有代表性,故A选项不符合题意;
B.为了解万象城某专卖店的平均营业额,选在周末进行调查,不具有代表性,故B选项不符合题意;
C.为了解某校1500名学生的视力情况,随机抽取该校150名学生进行调查,具有代表性,故C选项符合题意;
D.为了解全校学生课外小组的活动情况,对该校的女生进行调查,不具有代表性,故D选项不符合题意;
故选:C.
五.用样本估计总体
10.解:该农户卖脐橙的收入为:(35+35+34+39+37)÷5×44×5=7920(元).
故答案为:7920.
11.解:(1)根据表格可得该市今年的空气质量主要是良;
(2)该市今年空气质量级别为优和良的天数:×365=292(天);
(3)减少废气的排放;多植树;对垃圾及时的进行处理并且可回收的垃圾与不可回收的垃圾分开.
12.解:(1)a=0.9+0.3=1.2,b=1.2+0.2=1.4;
(2)根据用车意愿调查结果,抽取的100名师生每人每天使用A品牌共享单车的平均车费为:
×(0×5+0.5×15+0.9×10+1.2×30+1.4×25+1.5×15)=1.1(元),
所以估计5000名师生一天使用共享单车的费用为:5000×1.1=5500(元),
因为5500<5800,
故收费调整后,此运营商在该校投放A品牌共享单车不能获利.
六.频数与频率
13.解:在“Novelcoronavirus”中,字母的总数是16,字母“n”有2个,
因而字母“n”出现的频率是:=.
故选:B.
14.解:小丽抛一枚硬币10次,6次正面朝上,4次反面朝上,则正面朝上的频数是6,反面朝上的频数是4.
故选:C.
七.频数(率)分布表
15.解:∵数据的最大值是132,最小值是89,
∴极差为132﹣89=43,
又∵组距为5,
∴43÷5=8.6,
∴组数为9,
故选:C.
八.频数(率)分布直方图
16.解:由直方图可得,
抽取的男生中身高在169.5cm~174.5cm之间的男生有:50﹣6﹣10﹣16﹣6=12(人),
故选:A.
17.解:(1)a=10÷200=0.05,b=200×0.20=40,c=62÷200=0.31,
即a,b,c的值分别为0.05,40,0.31;
(2)由频数分布表可知,50≤x<60对应的频数为10,
由(1)知b=40,
补全的频数分布直方图如右图所示;
(3)3000×(0.20+0.31)
=3000×0.51
=1530(人),
答:这次七年级参加竞赛的学生约有1530人参赛成绩被评为“B”等级.
九.频数(率)分布折线图
18.解:由图知,英才班的全体人数为:10+20+25+5=60(人),
选择“东风快递”的学生人数为:20人,
∴选择“东风快递”的学生人数与全班人数的比值为:=.
故答案为:.
十.统计表
19.解:60×(1﹣35%﹣15%﹣10%)=24(人),
故选:D.
十一.扇形统计图
20.解:360°×(1﹣10%﹣20%﹣30%)=144°,
故答案为:144.
十二.条形统计图
21.解:(1)由统计图可得,
初二年级被抽查了:10+10+20+30+20+10=100(人),
初三年级被抽查了:20+10+30+20+10+10=100(人),
故答案为:100,100;
初二年级的学生参加课外活动的平均次数是
=2.7(次),
初三年级的学生参加课外活动的平均次数是:
=2.2(次),
即初二、初三年级的学生参加课外活动的平均次数分别为2.7次,2.2次;
(3)初二在参加课外活动方面,可能更好一些.
理由:初二学生不用面临毕业考试,学习压力不算大,可以有较多的时间参加课外活动,而初三的学生面临升学考试,学习压力大,相对参加课外活动的时间就少一些.
22.解:(1)被调查的学生共有:20÷20%=100(人);
在扇形统计图中,D所占的百分比为:×100%=35%,
故B所对应的圆心角的度数为:360°×(1﹣20%﹣30%﹣35%)=54°.
故答案为:100;54°.
(2)B的人数为:100×15%=15(人),C的人数为:100×30%=30(人),
补充完整如图所示:
(3)该校选定“汉风传统彩绘艺术”项目的人数大约有:1600×35%=560(人).
十三.折线统计图
23.解:(1)(12+15+13+14)÷200×100%=27%.
所以种植西红柿所占的百分比为27%;
(2)30%×200=60(人),
60﹣15﹣14﹣16=15(人).
答:(4)班选择种植大豆小组的学生人数为15人,
(3)2500×(1﹣30%﹣5%﹣27%)
=950(人).
答:估计该校学生选择种植玉米小组的人数为950人.
十四.统计图的选择
24.解:由于需要了解我国城乡居民收入10年来的变化趋势,所以适合采用的统计图是折线统计图,
故答案为:折线统计图.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
