2021-2022学年华东师大版八年级上学期数学第14章勾股定理周清试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级上学期数学第14章勾股定理周清试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 562.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-19 11:36:33 | ||
图片预览



文档简介
新华师大版八年级上册数学
第14章 勾股定理周清试卷
姓名____________ 时间: 60分钟 满分:100分 总分____________
考生注意: 1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,共100分,考试时间60分钟.
2.请将各题答案直接答在试卷上.
3.请注意答题严谨、书写规范.
第Ⅰ卷(选择题 共40分)
一、选择题(每小题4分,共40分)
1. 以下列各组数为边长,能组成直角三角形的是 【 】
(A)5 , 8 , 10 (B)4 , 5 , 6
(C)8 , 15 , 17 (D)8 , 39 , 40
2. 如图所示,在正方形网格中,每个小正方形的边长为1,则△ABC中,边长为无理数的边数为 【 】
(A)0 (B)1 (C)2 (D)3
3. 如图所示,在△ABC中,,则图中阴影部分的面积为 【 】
(A)12 (B)24 (C)36 (D)48
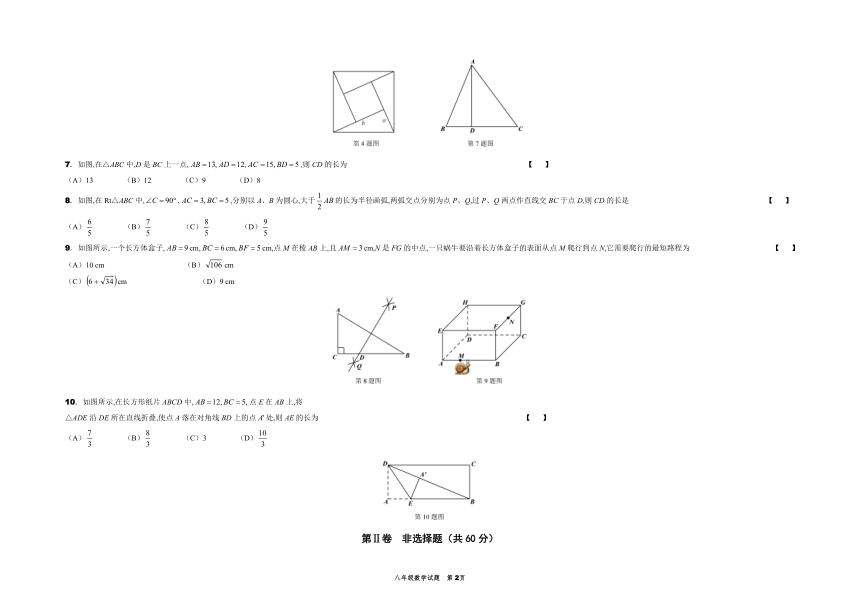
4. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).如果大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边长分别为,那么的值是 【 】
(A)4 (B)3 (C)2 (D)1
5. 已知直角三角形的两边长满足,则该直角三角形的第三边的长为 【 】
(A)5 (B) (C)5或 (D)
6. 已知是△ABC的三边,且,则△ABC是 【 】
(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)等腰三角形
7. 如图,在△ABC中,D是BC上一点,,则CD的长为 【 】
(A)13 (B)12 (C)9 (D)8
8. 如图,在Rt△ABC中,,,分别以A、B为圆心,大于的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是 【 】
(A) (B) (C) (D)
9. 如图所示,一个长方体盒子,cm,cm,cm,点M在棱AB上,且cm,N是FG的中点,一只蜗牛要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为 【 】
(A)10 cm (B)cm
(C)cm (D)9 cm
10. 如图所示,在长方形纸片ABCD中,点E在AB上,将
△ADE沿DE所在直线折叠,使点A落在对角线BD上的点处,则AE的长为 【 】
(A) (B) (C)3 (D)
第Ⅱ卷 非选择题(共60分)
二、填空题(每小题4分,共20分)
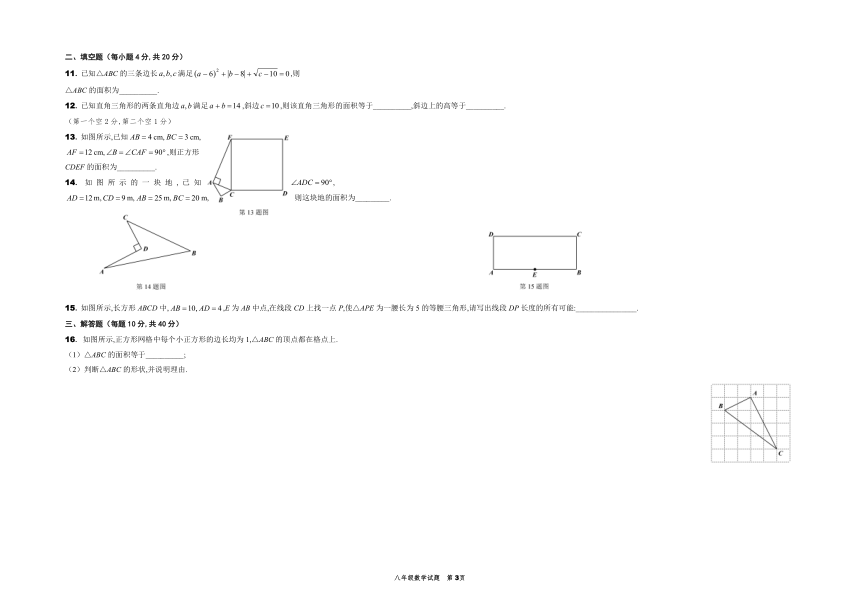
11. 已知△ABC的三条边长满足,则
△ABC的面积为__________.
12. 已知直角三角形的两条直角边满足,斜边,则该直角三角形的面积等于__________,斜边上的高等于__________.
(第一个空2分,第二个空1分)
13. 如图所示,已知cm,cm,
cm,,则正方形
CDEF的面积为__________.
14. 如图所示的一块地,已知,
m,m,m,m,则这块地的面积为_________.
15. 如图所示,长方形ABCD中,,E为AB中点,在线段CD上找一点P,使△APE为一腰长为5的等腰三角形,请写出线段DP长度的所有可能:________________.
三、解答题(每题10分,共40分)
16. 如图所示,正方形网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)△ABC的面积等于__________;
(2)判断△ABC的形状,并说明理由.
17. 如图,在△ABC中,,D为BC上一点,,求AB的长.
18. 如图,在离水面高度为8 m的岸上,有人用绳子拉船靠岸(假设绳子是直的),开始时绳子BC的长为17 m,此人以1 m/s的速度收绳,7 s后船移动到点D的位置,求船向岸边移动的距离.
19. 如图所示,在长方形ABCD中,,现将该长方形沿对角线BD折叠,使点C落在点处,交AD于点E.
(1)求证:;
(2)求AE的长;
(3)求△DEB的面积.
新华师大版八年级上册数学
第14章 勾股定理周清试卷答案解析
第Ⅰ卷(选择题 共40分)
一、选择题(每小题4分,共40分)
题号 1 2 3 4 5
答案 C C B D C
题号 6 7 8 9 10
答案 B C C A D
第Ⅱ卷 非选择题(共60分)
二、填空题(每小题4分,共20分)
11. 24 12. 24 (或4. 8) 13. 169 cm2
14. 96 m2 15. 2或3或8
部分选择题、填空题答案提示
8. 如图,在Rt△ABC中,,,分别以A、B为圆心,大于的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是 【 】
(A) (B) (C) (D)
解析 本题考查尺规作图、垂直平分线的性质定理以及勾股定理.
连结AD,如图所示.
由尺规作图可知:直线PQ垂直平分AB
∴
设,则
在Rt△ACD中,由勾股定理得:
∴
解之得:
∴,选择答案【 C 】.
9. 如图所示,一个长方体盒子,cm,cm,cm,点M在棱AB上,且cm,N是FG的中点,一只蜗牛要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为 【 】
(A)10 cm (B)cm
(C)cm (D)9 cm
解析 本题以立体图形上的最短路径问题为背景,考查勾股定理.把立体图形展开为平面图形,依据“两点之间,线段最短”,根据勾股定理求解最短路径长.若展开方式不唯一,则比较各个展开结果,取最小值作为最短路径长.
按如图(1)所示方式展开,由勾股定理得:
cm;
按如图(2)所示方式展开,由勾股定理得:
cm.
∵
∴它需要爬行的最短路程为10 cm,选择答案【 A 】.
10. 如图所示,在长方形纸片ABCD中,点E在AB上,将
△ADE沿DE所在直线折叠,使点A落在对角线BD上的点处,则AE的长为 【 】
(A) (B) (C)3 (D)
解析 本题考查勾股定理与方程思想.当直角三角形一条边长确定,其余两条边存在数量关系(即可以用一个未知数表示)时,可设出未知数,根据勾股定理建立方程进行求解.
在Rt△ABD中,由勾股定理得:
由折叠可知:
∴
设,则
在Rt△中,由勾股定理得:
∴
解之得:
∴,选择答案【 D 】.
15. 如图所示,长方形ABCD中,,E为AB中点,在线段CD上找一点P,使△APE为一腰长为5的等腰三角形,请写出线段DP长度的所有可能:________________.
解析 本题考查等腰三角形的存在性和勾股定理.参见《等腰三角形的存在性问题》.
分别如图1、图2、图3所示.(以下求解过程略)
在图1中,求得:;
在图2中,求得:;
在图3中,求得:.
综上所述,或或.
16. 如图所示,正方形网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)△ABC的面积等于__________;
(2)判断△ABC的形状,并说明理由.
解:(1)5 ;…………………………………………………………………3分
提示:如图所示,;
(2)△ABC是直角三角形. ………………………………………………4分
理由如下:由勾股定理得:
,
………………………………………………………………………………7分
∴
∴△ABC是直角三角形.…………………………………………………10分
17. 如图,在△ABC中,,D为BC上一点,,求AB的长.
解:在△ACD中
∵,
∴
∴
∴△ACD是直角三角形,且……………………………………5分
∵
∴
在Rt△ABC中,由勾股定理得:
∴.………………………………………………10分
18. 如图,在离水面高度为8 m的岸上,有人用绳子拉船靠岸(假设绳子是直的),开始时绳子BC的长为17 m,此人以1 m/s的速度收绳,7 s后船移动到点D的位置,求船向岸边移动的距离.
解:由题意可知:m,m.
在Rt△ABC中,由勾股定理得:
∴m………………………………4分
在Rt△ACD中,由勾股定理得:
∴m………………………………8分
∴m…………………………………………10分
答:船向岸边移动的距离为9 m.
19. 如图所示,在长方形ABCD中,,现将该长方形沿对角线BD折叠,使点C落在点处,交AD于点E.
(1)求证:;
(2)求AE的长;
(3)求△DEB的面积.
(1)证明:由折叠可知:
∵四边形ABCD是长方形
∴
∴
∴
∴;……………………………………………………………3分
(2)解:设,则
∵四边形ABCD是长方形
∴
在Rt△ABE中,由勾股定理得:
∴
解之得:
∴;…………………………………………………………………7分
(3)由(2)可知:
∴
……………………………………………………………………………10分
练 如图(6)所示,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应该滑动 【 】
(A)11米 (B)12米
(C)13米 (D)14米
八年级数学试题 第1页
第14章 勾股定理周清试卷
姓名____________ 时间: 60分钟 满分:100分 总分____________
考生注意: 1.本试卷分第Ⅰ卷(选择题)和第二卷(非选择题)两部分,共100分,考试时间60分钟.
2.请将各题答案直接答在试卷上.
3.请注意答题严谨、书写规范.
第Ⅰ卷(选择题 共40分)
一、选择题(每小题4分,共40分)
1. 以下列各组数为边长,能组成直角三角形的是 【 】
(A)5 , 8 , 10 (B)4 , 5 , 6
(C)8 , 15 , 17 (D)8 , 39 , 40
2. 如图所示,在正方形网格中,每个小正方形的边长为1,则△ABC中,边长为无理数的边数为 【 】
(A)0 (B)1 (C)2 (D)3
3. 如图所示,在△ABC中,,则图中阴影部分的面积为 【 】
(A)12 (B)24 (C)36 (D)48
4. 我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图).如果大正方形的面积为13,小正方形的面积是1,直角三角形的两直角边长分别为,那么的值是 【 】
(A)4 (B)3 (C)2 (D)1
5. 已知直角三角形的两边长满足,则该直角三角形的第三边的长为 【 】
(A)5 (B) (C)5或 (D)
6. 已知是△ABC的三边,且,则△ABC是 【 】
(A)锐角三角形 (B)直角三角形
(C)钝角三角形 (D)等腰三角形
7. 如图,在△ABC中,D是BC上一点,,则CD的长为 【 】
(A)13 (B)12 (C)9 (D)8
8. 如图,在Rt△ABC中,,,分别以A、B为圆心,大于的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是 【 】
(A) (B) (C) (D)
9. 如图所示,一个长方体盒子,cm,cm,cm,点M在棱AB上,且cm,N是FG的中点,一只蜗牛要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为 【 】
(A)10 cm (B)cm
(C)cm (D)9 cm
10. 如图所示,在长方形纸片ABCD中,点E在AB上,将
△ADE沿DE所在直线折叠,使点A落在对角线BD上的点处,则AE的长为 【 】
(A) (B) (C)3 (D)
第Ⅱ卷 非选择题(共60分)
二、填空题(每小题4分,共20分)
11. 已知△ABC的三条边长满足,则
△ABC的面积为__________.
12. 已知直角三角形的两条直角边满足,斜边,则该直角三角形的面积等于__________,斜边上的高等于__________.
(第一个空2分,第二个空1分)
13. 如图所示,已知cm,cm,
cm,,则正方形
CDEF的面积为__________.
14. 如图所示的一块地,已知,
m,m,m,m,则这块地的面积为_________.
15. 如图所示,长方形ABCD中,,E为AB中点,在线段CD上找一点P,使△APE为一腰长为5的等腰三角形,请写出线段DP长度的所有可能:________________.
三、解答题(每题10分,共40分)
16. 如图所示,正方形网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)△ABC的面积等于__________;
(2)判断△ABC的形状,并说明理由.
17. 如图,在△ABC中,,D为BC上一点,,求AB的长.
18. 如图,在离水面高度为8 m的岸上,有人用绳子拉船靠岸(假设绳子是直的),开始时绳子BC的长为17 m,此人以1 m/s的速度收绳,7 s后船移动到点D的位置,求船向岸边移动的距离.
19. 如图所示,在长方形ABCD中,,现将该长方形沿对角线BD折叠,使点C落在点处,交AD于点E.
(1)求证:;
(2)求AE的长;
(3)求△DEB的面积.
新华师大版八年级上册数学
第14章 勾股定理周清试卷答案解析
第Ⅰ卷(选择题 共40分)
一、选择题(每小题4分,共40分)
题号 1 2 3 4 5
答案 C C B D C
题号 6 7 8 9 10
答案 B C C A D
第Ⅱ卷 非选择题(共60分)
二、填空题(每小题4分,共20分)
11. 24 12. 24 (或4. 8) 13. 169 cm2
14. 96 m2 15. 2或3或8
部分选择题、填空题答案提示
8. 如图,在Rt△ABC中,,,分别以A、B为圆心,大于的长为半径画弧,两弧交点分别为点P、Q,过P、Q两点作直线交BC于点D,则CD的长是 【 】
(A) (B) (C) (D)
解析 本题考查尺规作图、垂直平分线的性质定理以及勾股定理.
连结AD,如图所示.
由尺规作图可知:直线PQ垂直平分AB
∴
设,则
在Rt△ACD中,由勾股定理得:
∴
解之得:
∴,选择答案【 C 】.
9. 如图所示,一个长方体盒子,cm,cm,cm,点M在棱AB上,且cm,N是FG的中点,一只蜗牛要沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为 【 】
(A)10 cm (B)cm
(C)cm (D)9 cm
解析 本题以立体图形上的最短路径问题为背景,考查勾股定理.把立体图形展开为平面图形,依据“两点之间,线段最短”,根据勾股定理求解最短路径长.若展开方式不唯一,则比较各个展开结果,取最小值作为最短路径长.
按如图(1)所示方式展开,由勾股定理得:
cm;
按如图(2)所示方式展开,由勾股定理得:
cm.
∵
∴它需要爬行的最短路程为10 cm,选择答案【 A 】.
10. 如图所示,在长方形纸片ABCD中,点E在AB上,将
△ADE沿DE所在直线折叠,使点A落在对角线BD上的点处,则AE的长为 【 】
(A) (B) (C)3 (D)
解析 本题考查勾股定理与方程思想.当直角三角形一条边长确定,其余两条边存在数量关系(即可以用一个未知数表示)时,可设出未知数,根据勾股定理建立方程进行求解.
在Rt△ABD中,由勾股定理得:
由折叠可知:
∴
设,则
在Rt△中,由勾股定理得:
∴
解之得:
∴,选择答案【 D 】.
15. 如图所示,长方形ABCD中,,E为AB中点,在线段CD上找一点P,使△APE为一腰长为5的等腰三角形,请写出线段DP长度的所有可能:________________.
解析 本题考查等腰三角形的存在性和勾股定理.参见《等腰三角形的存在性问题》.
分别如图1、图2、图3所示.(以下求解过程略)
在图1中,求得:;
在图2中,求得:;
在图3中,求得:.
综上所述,或或.
16. 如图所示,正方形网格中每个小正方形的边长均为1,△ABC的顶点都在格点上.
(1)△ABC的面积等于__________;
(2)判断△ABC的形状,并说明理由.
解:(1)5 ;…………………………………………………………………3分
提示:如图所示,;
(2)△ABC是直角三角形. ………………………………………………4分
理由如下:由勾股定理得:
,
………………………………………………………………………………7分
∴
∴△ABC是直角三角形.…………………………………………………10分
17. 如图,在△ABC中,,D为BC上一点,,求AB的长.
解:在△ACD中
∵,
∴
∴
∴△ACD是直角三角形,且……………………………………5分
∵
∴
在Rt△ABC中,由勾股定理得:
∴.………………………………………………10分
18. 如图,在离水面高度为8 m的岸上,有人用绳子拉船靠岸(假设绳子是直的),开始时绳子BC的长为17 m,此人以1 m/s的速度收绳,7 s后船移动到点D的位置,求船向岸边移动的距离.
解:由题意可知:m,m.
在Rt△ABC中,由勾股定理得:
∴m………………………………4分
在Rt△ACD中,由勾股定理得:
∴m………………………………8分
∴m…………………………………………10分
答:船向岸边移动的距离为9 m.
19. 如图所示,在长方形ABCD中,,现将该长方形沿对角线BD折叠,使点C落在点处,交AD于点E.
(1)求证:;
(2)求AE的长;
(3)求△DEB的面积.
(1)证明:由折叠可知:
∵四边形ABCD是长方形
∴
∴
∴
∴;……………………………………………………………3分
(2)解:设,则
∵四边形ABCD是长方形
∴
在Rt△ABE中,由勾股定理得:
∴
解之得:
∴;…………………………………………………………………7分
(3)由(2)可知:
∴
……………………………………………………………………………10分
练 如图(6)所示,一架梯子长25米,斜靠在一面墙上,梯子顶端离地面15米,要使梯子顶端离地24米,则梯子的底部在水平方向上应该滑动 【 】
(A)11米 (B)12米
(C)13米 (D)14米
八年级数学试题 第1页
